基于模块密度的差分进化社区发现技术

刘 彩 虹

(大连外国语大学 计算机教研部, 辽宁 大连　116041)



基于模块密度的差分进化社区发现技术

刘 彩 虹

(大连外国语大学 计算机教研部, 辽宁 大连116041)

摘要:提出了一种基于模块密度的差分进化社区发现算法(community detection based on differential evolutionary algorithm, CDDEA).在CDDEA算法中,通过调节一个参数可以识别出不同层次的社区结构.在真实世界网络和计算机人工合成网络上的实验表明,CDDEA能够有效探测复杂网络中的社区结构.

关键词:复杂网络; 社区发现; 差分进化; 模块密度

为了清晰的了解复杂网络的结构特性和功能特性,越来越多的研究者开始关注复杂网络中的社区发现问题[1-5].一些常见的复杂网络包括社交网络、生物网络,以及万维网络等.这些复杂网络都以节点和边的形式来表示其结构.因此,找出这些节点和边的关系对于研究其组成,理解其功能特性显得尤为重要.社区结构探测作为一种能够揭示网络中节点和边关系的方法,已经成为网络科学中一个得到广泛研究的基本问题.

大量的理论研究和实践表明,复杂网络拥有一些重要的属性特征.例如,社区结构内部关系紧密,社区结构之间关系松散.根据这一属性,众多学者提出了许多有效的社区发现方法,文献[3]对此有详细的阐述.在这些方法中,一种比较常用的方法就是将社区发现问题转化为对模块度函数的优化问题,从而找到对网络结构的最优划分[6].目前许多方法都是依据这一方法提出的改进算法.但是,搜索最大模块度是一个NP难题,因为和任何复杂网络相比,社区划分的增长空间增加较快,也就是说,模块度是一个与网络规模有关的度量标准.因此,发现一个比预期值较小的社区结构是不可能的.这个问题也叫做模块度的分辨率限制问题[7].为了解决基于模块度方法存在的分辨率限制问题,Li等[8]提出了一种新的函数,叫模块密度,通过计算社区内部与社区之间的连边之差与社区所含的节点数的比值,来定义社区的结构特征,从而解决模块度分辨率的限制问题.

差分进化算法由Storn和Price提出[9],是一种基于种群的随机并行搜索算法.与传统的遗传算法相比[10],存在以下优点:差分进化算法在变异策略中采用多个个体的基因信息,这样能充分利用种群的分布多样性,提高算法的搜索能力.另外,它还具有较快的收敛能力.特别是,在优化问题中,差分进化算法能表现出较好的性能.

作为复杂网络的一个新的研究方向,进化算法在复杂网络方面的应用已经得到了许多研究者的关注,例如, Tasgin等[11]提出了基于模块度的遗传算法的社区发现方法;Pizzuti[12]提出了一种基于社区得分的遗传算法的社区发现方法,通过优化社区得分函数来寻找最优的社区划分;Gong等[13]提出了基于文化算法的社区发现方法,它是在遗传算法的基础上增加局部搜索来寻找最优社区划分;Amiri等[4]提出了多目标萤火虫算法的社区发现方法,并采用社区得分和社区适应度作为目标优化函数,来寻找较优的社区结构划分.Jia[14]等提出了一种基于模块度的差分进化社区发现方法,该方法在差分变异阶段,没有利用当前种群中最优个体信息来生成下一代个体,导致种群的进化速度较慢;另外,由于该算法采用模块度作为优化函数,使该算法探测社区的效果不佳.虽然上述这些算法能够对复杂网络中的网络结构进行有效的划分,但这些算法在社区划分精度方面仍有一定的提升空间.

本文提出了一种基于模块密度的差分进化社区发现方法.通过调节模块密度中参数λ的大小来得到不同层次的社区结构.另外,在划分网络结构的过程中,CDDEA算法不需要任何诸如社区数目等社区结构的先验信息,这对于缺少先验信息的真实网络是非常重要的.

1模块度与模块密度

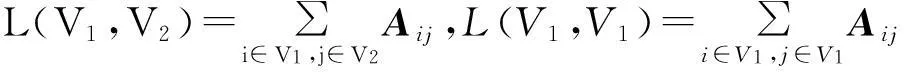
(1)

根据上述模块度函数,可以看到模块度的主要思想来源于真实社区和无结构的随机网络的社区结构的比较,然而,Fortunato和Barthelemy[7]指出模块度在发掘有效社区方面的效果并不理想,并且认为其划分的社区大小依赖于整个网络.因此,不可能找到比预定值更小的社区结构.

为了解决模块度在社区发现方面的局限性,Li等[8]提出了基于模块密度的社区划分方法,模块密度的定义如下:

(2)

通过将网络划分Gi内的节点度数与外的节点度数的差值与子网络进行比值计算,能有效的测试社区划分的合理性.D的值越大,划分越准确.因此,社区划分问题可以转换为求模块密度的最大化问题.在经过一系列理论和实践测试后,Li等人证明了模块密度与核值的等价性,并提出了一个更具有通用性的模块密度计算方法:

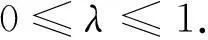
(3)

如果λ=1,则Dλ等价于比率关联(ratio association);如果λ=0,则Dλ等价于比率割集(ratio cut);如果λ=0.5,则Dλ为模块密度.也就是说,模块密度可以看作是比率关联与比率割集的组合.通过优化比率关联,可以将网络结构划分为较小的社区;通过优化比率割集,可以将网络结构划分为较大的社区.根据这个公式,可以通过调节参数λ来分析复杂网络的拓扑结构和层次结构.最终,解决模块度在社区发现中的分辨率限制性问题.

2CDDEA算法

这部分将解释CDDEA算法的原理.首先介绍了差分进化算法,然后详细阐述了CDDEA算法的细节.Strorn和Price[9]提出的差分进化算法已广泛应用于求解非线性和多目标函数问题,并且差分进化也是一种优化问题的较好方法.它与遗传算法很相似,但又有所不同.最突出的不同在于差分进化能充分利用种群的多样性.DE的重要算子有变异,交叉和选择.首先,随机初始化种群,然后选择差分变异策略,最后执行交叉操作.并且选择最好的个体传入下一代.

2.1个体表示方式

对于一个网络,G=(V,E),V是节点集合,E是边的集合,节点数目为n.一个个体可以表示成下列形式:

inividualj={c_id1,…,c_idi,…,c_idn}

inividualj表示种群中第j个个体,c_idi表示节点i属于社区c_idi,即社区ID值.例如,如果c_id5=3,表示第五个节点属于第三个社区.在初始化过程中,每个节点被赋予不同的社区,例如{1,2,…,n}.然而,这样做会没有充分利用网络的结构信息,因为任何相邻的节点可能属于同一个社区.这里使用一个启发式,对于每个个体随机选择一些节点,并将它们的社区ID值赋给其邻居节点.例如,图1a表示9个演员和14条关系构成的一个小型社会网络.

对于图1a所示的简单网络,使用图1b来展示个体表示和种群初始化的方式.通过图1b,可以清楚地表示每个节点的社团ID值,以及如何利用网络的初始结构信息来初始化个体.例如,如果节点v2被选中,那么将其社区ID赋值给邻居节点v1和v3,从而节点v1和v3的社区ID值也变为2.

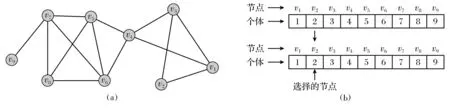
图1　一个简单的社会网络及其个体表示方式

2.2差分变异

在经过种群初始化后,差分进化算法(DE)将通过差分变异来生成新的个体.目前,有4种不同的差分变异策略:

① DE/rand/1

② DE/best/1

③ DE/best/2

④ DE/rand-to-best/1

图2　变异后产生的后代个体

首先,从当前种群中选择模块密度最大的个体;其次,计算该个体与另一个随机个体的差分结果值,再乘以贪婪因子ω;然后,再随机选择当前种群中的两个随机个体,计算它们的差分结果值,并乘以放大因子F;最后,将当前个体与这两个差分结果值相加,求和,计算新产生的个体的社区ID值.当然,采取该变异策略后得到的社区ID值会超过节点的社区标识范围,例如图2a的节点v6和v9,这些值是没有实际意义的,一个是负值,一个是大于节点的社区标识.这时,采用其邻居节点的社区ID值对这些节点的社区ID进行重新标识.如果其邻居节点的社区ID值存在多个,则随机从其中选择一个.例如图2b所示,节点v6和v9的社区ID值被赋予2.

2.3交叉

为了增强种群的多样性,父代个体Xi(t)与经过差分变异后产生的新个体Xi(t+1)进行交叉操作,最常见的交叉方法如下式所示[9]:

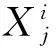
然而,这种交叉策略并不适用于CDDEA算法.因为对每个节点的社区ID进行初始赋值时,是根据网络的初始结构信息,采用标签传播策略来更新与该节点相邻的邻居节点的社区ID值,那么,对于各个个体而言,由于随机选择的初始节点

存在差异,导致由该初始节点传递至其邻居节点的社区ID也存在不同.也就是说,不同个体中的相同社区ID可以表示不同的社区;不同社区ID表示的节点也可能存在于同一个社区中.例如,在图3中,个体1和个体2中的社区ID2对应的个体属于不同的社区;而个体1中的社区ID4对应的节点与个体2中社区ID2对应的节点属于同一个社区.

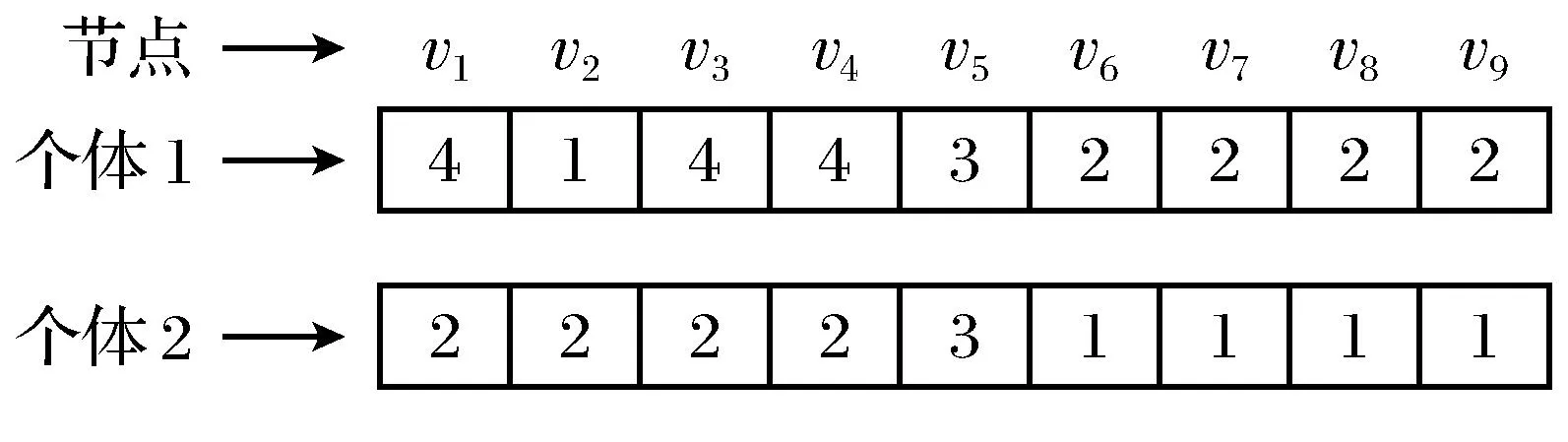
图3　两个个体

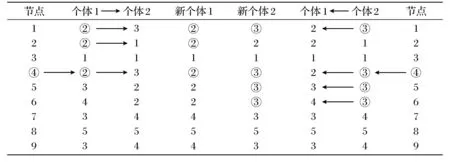
因此,在CDDEA算法中,采用双路交叉策略[10,12-13].对于两个个体,个体1与个体2,随机选择一个节点,并将该节点的社区ID值以及该个体中与该ID值相同的所有节点的社区ID值赋值给另外一个个体,完成交叉操作.例如在表1中,随机选择一个节点v4.然后,通过个体交叉,将节点v4以及与其具有相同社区ID值得节点社区ID信息传递给新的个体.

从计算结果看：No1轴承发热量最大，达到315.6W，No5轴承发热量最小，为71.9W；No2、No3和No4轴承的发热量接近。

2.4选择

如果交叉的后代个体Xi(t+1)具有比Xi(t)个体的更高的模块密度值,则它在下一代将取代Xi(t);否则,Xi(t)将保留至下一代种群中.通常称子为贪婪选择策略.换句话说,一个个体的选择是通过其模块密度值的大小来确定的,而这些具有较高模块密度值的个体将有更多被选中的机会,并且,它们会将更优的社区ID信息传递给下一代.最终,通过在每一代群体中选择较优的个体,使得社区的划分向更好的方向进化.

在进化算法中,目标函数的选择对于较优的个体产生往往起着非常关键的作用.CDDEA采用模块密度作为适应度函数,在文中模块度与模块密度处已经对它的优点进行了比较详细的阐述.

CDDEA算法的具体步骤如下:

步骤1初始化算法参数:最大迭代次数Gmax;种群规模Psize;交叉概率Pc;伸缩因子F和贪婪因子ω;

步骤2按照2.1节的方法初始化种群,并计算每个个体的模块密度,在当前种群中找到最优的个体;

步骤3根据2.2节的方法,选择当前种群中的多个个体,以及步骤2得到的最优个体,执行差分变异操作,生成新的个体;

步骤4根据交叉概率Pc的大小,将当前种群中的个体与步骤3得到的经差分变异后生成的新个体进行交叉操作,生成新的个体;

步骤5计算从步骤4得到的每个后代的模块化密度.并在当前种群中,根据模块密度值的大小对这些后代个体排序;

步骤6根据当前种群中的个体和从步骤5排序得到的个体来选择较优的个体重构当前的种群,使其成为下一代的父代种群;

步骤7检查终止条件是否满足:如果迭代的预定数量达到Gmax,算法停止,并输出步骤5中产生的最优个体;否则,转到步骤3进行下一次迭代.

3实验结果

本文在真实网络和计算机人工合成网络上进行相关实验,以检验CDDEA在社区探测方面的效果.同时,与相关文献中的算法进行了对比,这些算法包括DECD[14], GA[10],GA-net[12], Meme-Net[13],Fast unfolding[16], Fast Newman[15], Leon Danon[17].在CDDEA算法中,各参数的设置如下:伸缩因子F=1.8,贪婪因子ω=1.0,交叉参数Pc=0.8,根据网络结构的复杂性,迭代次数的范围为50～200.由于基于进化算法的社区检测方法的结果依赖于随机搜索过程的有效性,在4个真实网络上进行了10～30次测试,并对不同的社区检测算法进行了对比分析.

3.1评价标准:互信息量NMI

目前,提出了许多社区划分方法,但不能合理的评价其探测社区结构的有效性.Danon等[17]提出了一个评价社区划分效果的标准:互信息量NMI.因此,本文也采用这一标准,其公式为

(4)

A和B是划分的两个社区,C是模糊矩阵,CA、CB是A和B两个划分的社团数目,Ci.、C.j是i行j列的元素的和.如果A=B,I(A,B)=1,则划分的社区与真实社区相同;否则,如果划分的社区与真实社区完全不相同,则I(A,B)=0.

3.2真实网络

表2～表5表示CDDEA与其他算法在4个真实网络:空手道俱乐部网络(Zachary’s Karate Club Network)[18]、海豚网络(The Bottlenose Dolphins Network)[19]、美国大学足球网络(The American College Football Network)[6]和美国政治图书网络(http:∥www.orgnet.com/)上运行30次所得到的社区探测的效果.由于这4个网络的结构性存在差异,本文对CDDEA算法中的模块密度函数中的参数λ进行调整,以便在网络结构复杂时提高对网络社区的探测能力.在表2中,λ=0.35;在表3和表5中,λ=0.41;在表4中,λ=0.81.

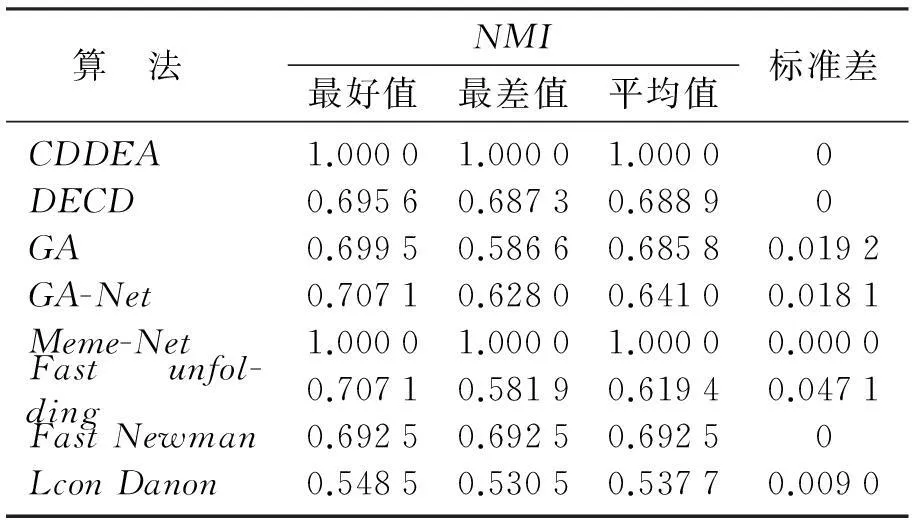
表2　八种算法在空手道俱乐部网络上获得的NMI值

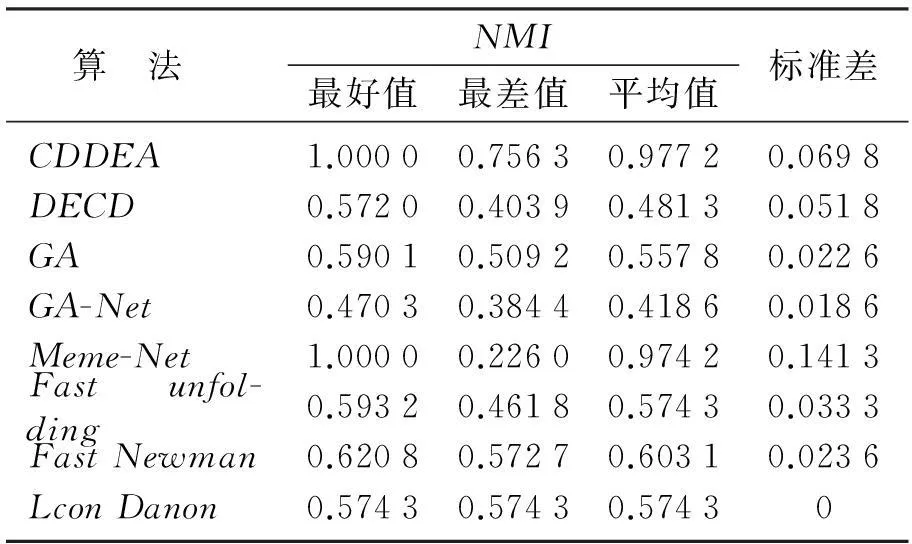
表3　8种算法在海豚网络上获得的NMI值

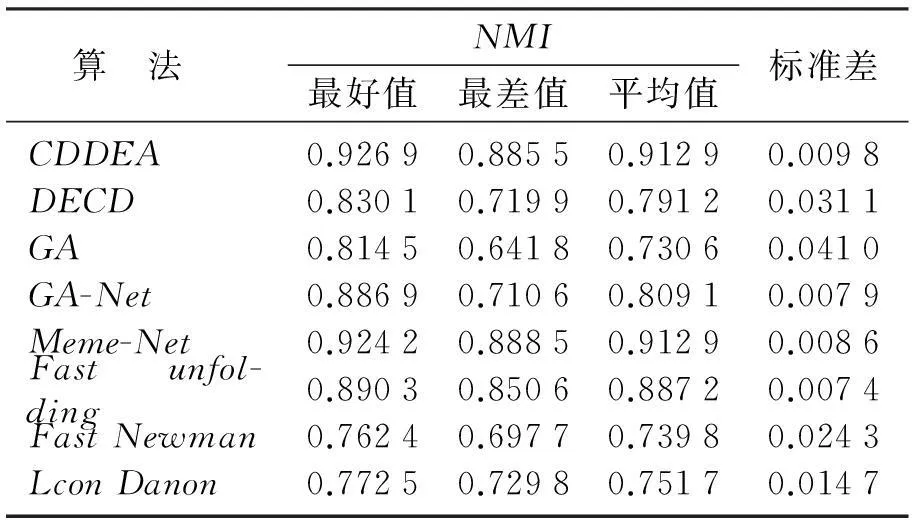
表4　8种算法在美国足球网络上获得的NMI值

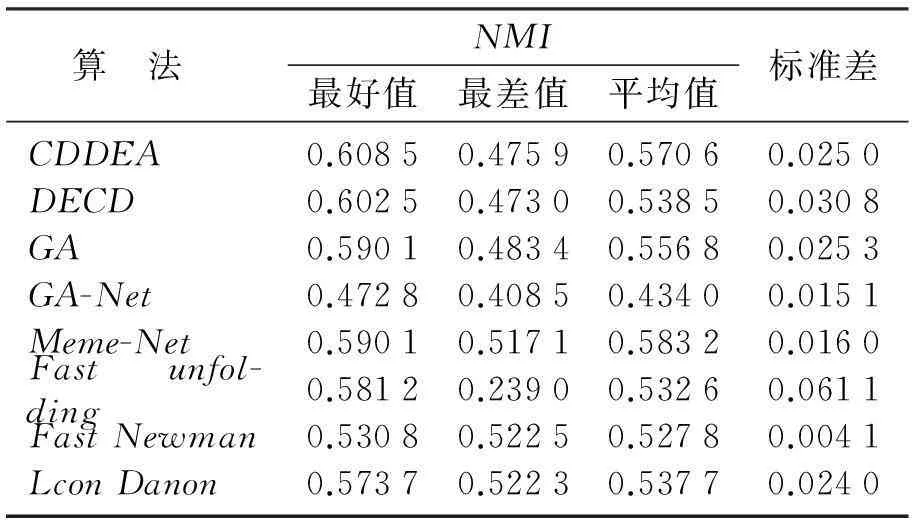
表5　8种算法在美国政治图书网络上获得的NMI值

从表2～表5可以看到,相对于其他算法而言,CDDEA在4个真实世界的网络上的社区发现具有较好的表现.在表2中,CDDEA得到的结果表明它能够全部收敛到全局最优NMI=1.换句话说,CDDEA运行30次后,每次所检测到的社区划分与真实的社区完全一致.在表3中,CDDEA方法在海豚网络上得到的平均NMI值为0.977 2,而Meme-Net获得的平均NMI值为0.974 2.在执行CDDEA和其他算法的过程中,本文记录了每种方法运行30次的值.对于CDDEA,得到了27次最佳值(NMI=1),得到NMI=0.804 71次,得到NMI=0.756 32次.对于Meme-Net,得到29次NMI为1的最佳值,得到NMI=0.226 01次.因此可见,算法在寻优过程中,容易陷入局部最优值.然而,相对于其他算法而言,CDDEA和Meme-Net在海豚网络上具有较好的性能.在表4中,大部分算法获得的性能非常接近.根据它们的平均NMI值,对这些算法的效果进行排序:CDDEA(0.912 9),Meme-Net(0.912 9),Fast unfolding(0.887 2),GA-NET(0.809 1),DECD(0.791 2),Leon Danon(0.751 7),Fast Newman(0.739 8),GA(0.730 6);在表5中,由于网络结构的复杂性,所有方法都不能找到真实的社区划分.

图4表明,随着λ值的变化,CDDEA能够在空手道俱乐部网络上得到不同层次的社区结构.当λ=0.35时,CDDEA能够发现2个社区,如图4a所示,这与真实的社区结构一致.当λ=0.45时,CDDEA能够发现3个社区,如图4b所示.可见,图4a中白色的社区被划分为2个更小的社区.当λ=0.55时,图4b中的黑色社区又被划分为2个较小的社区,如图4c所示.当λ=0.65时,节点24,28从图4c的黑色社区中移出,加入了灰色社区,如图4d所示.这是因为随着λ值的增加,CDDEA算法探测社区的能力也在增强,由于节点24,28与灰色社区内节点的交互较为紧密,所以这两个节点被正确的划入了灰色的社区.当λ=0.75时,节点24,27,28,30构成了一个新的分区,如图4e所示.但从图中可以看出,它们之间的交互并不紧密,比较松散.这是因为随着λ值的持续增加,CDDEA能够探测到一些更小的社区,但这些社区仅有很少几个节点组成.也就是说,这些节点组成的社区是没有实际意义的.因此,对于CDDEA算法而言,合理的设置λ值是非常重要的.如果希望以较高的分辨率探测网络的社区结构时,可以设置较大的λ值;如果希望以较低的分辨率探测网络的社区结构时,可以设置较小的λ值.当然,对于不同的网络结构,λ的值应处在一个合理的范围中,如果λ值太小,将不能得到有效的社区划分,很可能得到的仍然是原始网络;如果λ值太大,将得到许多无意义的社区.

图5表示CDDEA在海豚网络上大多数情况下探测到的社区结构.当λ=0.41时,CDDEA运行30次后获得的平均NMI值为0.977 2,其中,27次得到最佳NMI值1,也就是说,与真实网络的社区结构完全一致.图6表示,当λ=0.81时,CDDEA在美国大学足球网络上探测到的社区结构.CDDEA运行30次后获得的平均NMI值为0.912 9.由图6可知,CDDEA探测到13个分区,只是有少数几个节点存在社区划分误差.在美国政治图书网络上,与其他算法一样,由于网络结构的复杂性,CDDEA没有得到真实的社区结构,但CDDEA得到的最大NMI值为0.608 5,仍然优于其他算法.由图7可知,CDDEA得到了3个社区划分,与真实的社区个数完全一致.

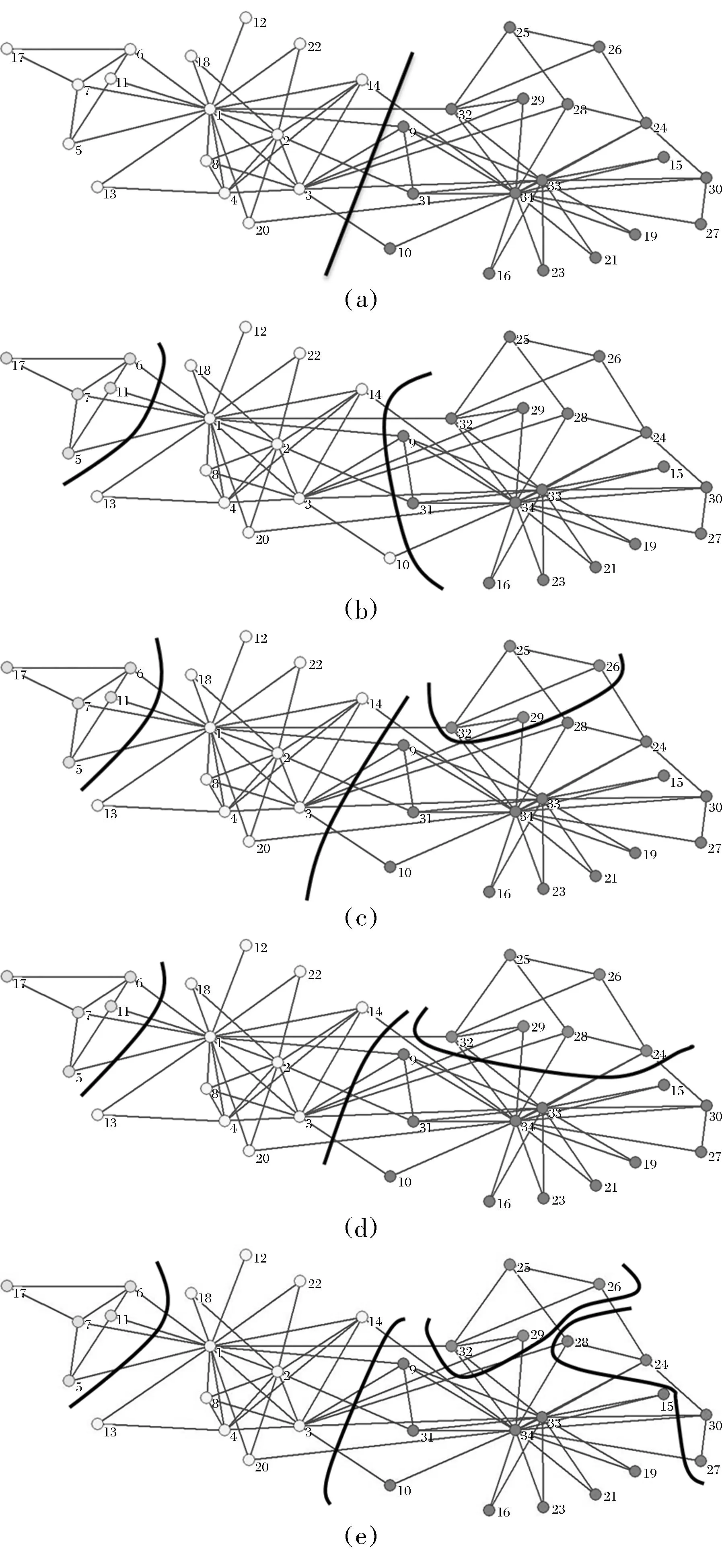
图4　随着λ值的变化,在空手道俱乐部网络上

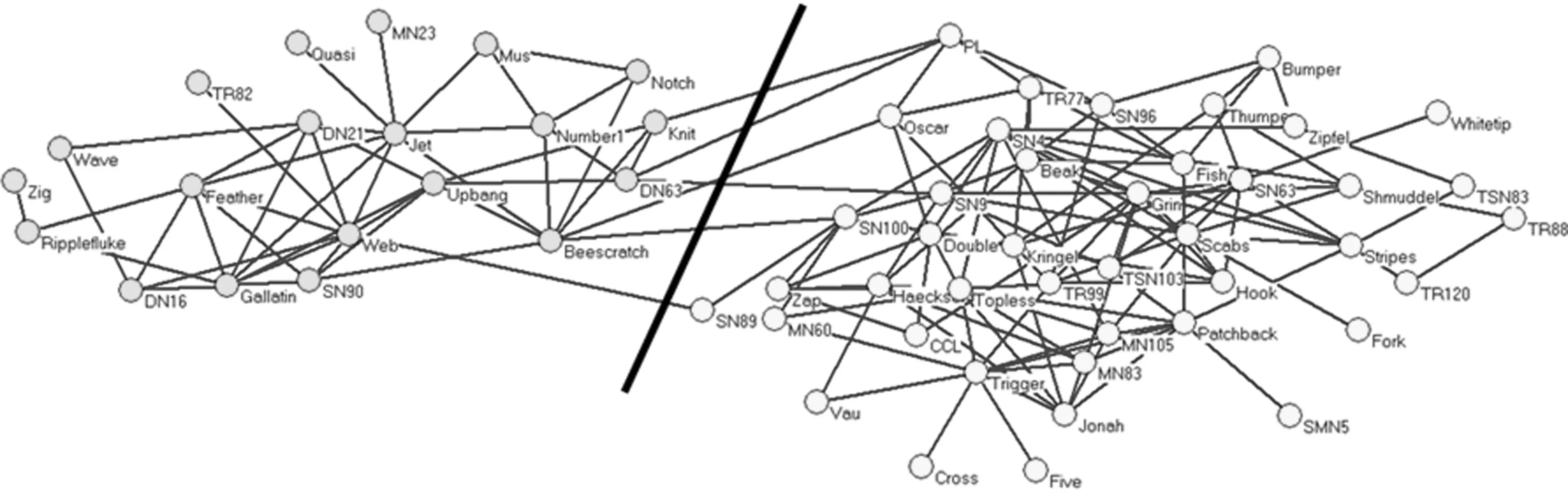
图5　在海豚网络上探测到的社区结构

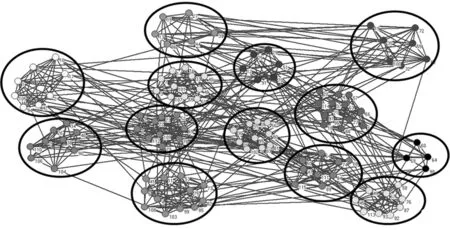
图6　在美国大学足球网络上探测到的社区结构

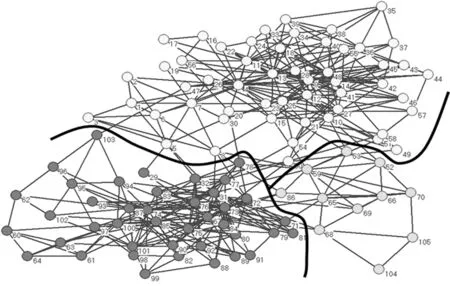
图7　在美国政治图书网络上探测到的社区结构

3.3计算机人工合成网络

另外,本文还使用Lancichinetti等人[20]的基准网络评价CDDEA的性能.它包含128个节点,分成4个社区,每个社区包含32个节点,每个节点的平均度为16,这里,μ是一个混合参数,当μ<0.5时,网络社区内的每个节点的邻居数目多于其他社区的邻居数目;同时,当μ≥0.5时,其社区内的每个节点的邻居等于或小于其他社区的邻居数目.换句话说,一个有效的社区检测方法应该能够发现μ<0.5时网络的社区结构.因此,本文利用这个人工网络来检验CDDEA社区划分的效果.对于这个基准网络,混合参数μ的变化范围为0～0.5,间隔为0.05,从而一共产生了11个不同的网络.在一般情况下,随着μ的增加,网络的社区检测将会变得越来越困难.

首先,对于这5种基于进化的社区发现算法,设置其最大迭代次数Gmax=250,变异概率为0.2.随着混合参数μ的增加,网络的结构也变得越来越复杂.根据不同的混合参数μ,总共得到11个不同的人工合成网络.针对网络结构的复杂性,分别设置不同的参数来提高CDDEA的社区探测性能,具体参数设置如表6所示.对于各个算法,运行10次取其平均值,得到的NMI值如图8所示.

表6　CDDEA在计算机人工合成网络上的参数设置情况

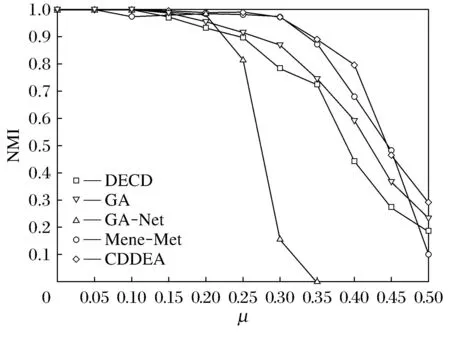
图8　在计算机人工合成网络上检测CDDEA探测

从图8可以看到,CDDEA在人工合成计算机网络上具有较好的社区探测性能.当μ≤0.25时,CDDEA发现的社区结构与真实社区基本一致.另外,与其他进化算法相比,CDDEA的社区探测效果优于GA和DECD,并且与Meme-net非常接近.随着μ的增加,社区的结构特征逐渐变得比较模糊,CDDEA依然能较好的发现社区的划分.例如,当μ=0.30时,CDDEA获得的平均NMI值接近于1;当μ=0.35时,CDDEA获得的平均NMI值接近于0.9,这表明此时探测到的社区划分与真实的社区划分非常接近.随着μ的继续增加,网络结构的复杂性导致了CDDEA探测真实社区难度的增加,但其得到的平均NMI值仍然接近于0.8,明显优于Meme-Net,GA,GA-Net和 DECD.当μ达到0.45或0.5时,网络的社区特征变得非常模糊,所有的算法都不能探测到真实的社区结构.

同时还发现,通过调节CDDEA中的参数,能够有效提高其探测社区的性能.通过调整λ的大小,可以从不同的分辨率上探测网络的社区结构:对于网络结构较为简单的网络,可以设置较小的λ值;对于网络结构较为复杂的网络,可以设置较大的λ值.通过调整贪婪因子ω和放大因子F,可以提高种群中各个个体的差分变异范围,提高种群的多样性,避免算法陷入局部极值.

4结论

本文提出了一种基于模块密度的差分进化社区发现算法CDDEA,并在4个真实世界的网络和计算机人工合成网络上测试了算法的有效性.同时,本文和其他算法进行了对比.实验结果表明, CDDEA能够有效探测到网络的社区划分.另外,由于CDDEA采用模块密度作为优化函数,能够有效解决模块度的分辨率限制问题,在不同分辨率上对网络结构进行合理的划分.在未来的工作中,将对CDDEA进行改进,以便其能够对动态网络和异构网络的社区进行有效探测.

参考文献:

[1] 于海,赵玉丽,崔坤,等. 一种基于交叉熵的社区发现算法[J]. 计算机学报, 2015,38(8):1574-1581.

(YU H, ZHAO Y L, CUI K, et al. Community detection algorithm based on cross-entropy method[J]. Chinese Journal of Computers, 2015,38(8):1574-1581.)

[2] 武森,卢丹,冯小东,等. 基于大规模复杂网络社区发现的科研合著网络分析[J]. 中国科技论文, 2014,9(4):474-478.

(WU S, LU D, FENG X D, et al. Analysis of scientific co-authorship network based on large-scale complex network community detection[J]. China Science Paper, 2014,9(4):474-478.)

[3] FORTUNATO S. Community detection in graphs[J]. Physics Reports, 2010,486(3):75-174.

[4] AMIRI B, HOSSAIN L, CRAWFORD J W, et al. Community detection in complex networks: multi-objective enhanced firefly algorithm[J]. Knowledge-Based Systems, 2013,46(1):1-11.

[5] CORNEIL D G, GOTLIEB C C. An efficient algorithm for graph isomorphism[J]. Journal of the ACM, 1970,17(1):51-64.

[6] NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004,69(2).

[7] FORTUNATO S, BARTHÉLEMY M. Resolution limit in community detection[J]. Proceedings of the National Academy of Sciences, 2007,104(1):36-41.

[8] LI Z, ZHANG S, WANG R S, et al. Quantitative function for community detection[J]. Physical Review E, 2008,77(3).

[9] STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997,11(4):341-359.

[10] 白鹭. 混合自适应性遗传算法[J]. 沈阳大学学报, 2010,22(3):14-17.

(BAI L. A mixed self-adaption genetic algorithm[J]. Journal of Shenyang University, 2010,22(3):14-17.)

[11] TASGIN M, BINGOL H. Community detection in complex networks using genetic algorithms[J]. arXiv preprint arXiv:0711.0491, 2007.

[12] PIZZUTI C. GA-net: a genetic algorithm for community detection in social networks[M]∥Parallel problem solving from nature-PPSN X. Berlin: Springer, 2008:1081-1090.

[13] GONG M, FU B, JIAO L, et al. Memetic algorithm for community detection in networks[J]. Physical Review E, 2011,84(5).

[14] JIA G, CAI Z, MUSOLESI M, et al. Community detection in social and biological networks using differential evolution[M]∥Learning and intelligent optimization. Berlin: Springer, 2012:71-85.

[15] NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004,69(6).

[16] BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008(10).

[17] DANON L, DIAZ-GUILERA A, DUCH J, et al. Comparing community structure identification[J]. Journal of Statistical Mechanics: Theory and Experiment, 2005(9).

[18] ZACHARY W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977:452-473.

[19] LUSSEAU D, SCHNEIDER K, BOISSEAU O J, et al. The bottlenose dolphin community of doubtful sound features a large proportion of long-lasting associations[J]. Behavioral Ecology and Sociobiology, 2003,54(4):396-405.

[20] LANCICHINETTI A, FORTUNATO S, RADICCHI F. Benchmark graphs for testing community detection algorithms[J]. Physical Review E, 2008,78(4).

【责任编辑: 肖景魁】

Community Detection Based on Differential Evolution by Using Modularity Density

LiuCaihong

(Department of Computer, Dalian University of Foreign Languages, Dalian 116044, China)

Abstract:A community detection based on differential evolutionary algorithm (CDDEA) is put forward. In CDDEA, different levels of community structures could be identified by adjusting a parameter. The experimental results on real world and synthetic networks show that CDDEA provides an effective method in discovering community structures in complex networks.

Key words:complex networks; community detection; differential evolution; modularity density

中图分类号:TP 393

文献标志码:A

文章编号:2095-5456(2016)02-0132-09

作者简介:刘彩虹(1981-),女,吉林德惠人,大连外国语大学讲师,博士研究生.

基金项目:辽宁省教育厅十二五规划项目(JG13DB242); 2013年大连外国语大学科研项目(2013XJQN20).

收稿日期:2015-10-19