直面差异 个性指导——《三角形内角和》教学片断与评析

王旭程 吴玉兰

新课程提出要以“尊重学生、直面差异”为出发点，即教学要正视学生的差异，重视学生的个性化需求，使每一位学生都受到适合的教育，获得最佳的发展。

《三角形内角和》是新思维小学《数学》四年级下册的学习内容。学习这一内容之前，我们对班中39位学生进行已有知识基础的调查，发现84.6%的学生知道三角形的内角和是180°。这33名学生中，主要有以下几种验证方法。

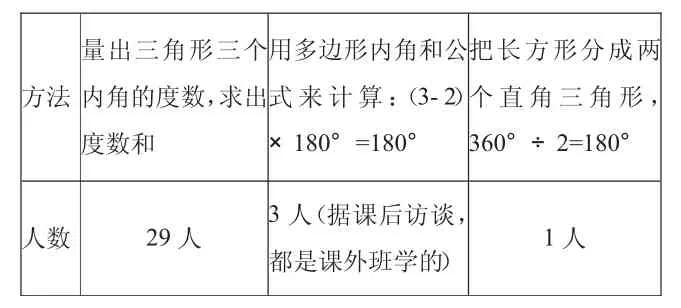
方法量出三角形三个内角的度数，求出度数和用多边形内角和公式来计算：（3-2）×180°=180°把长方形分成两个直角三角形，360°÷2=180°人数 29人 3人（据课后访谈，都是课外班学的） 1人

有学生提出，自己量出来三角形三个内角的和并不是180°，结论真的正确吗？看来，量的方法存在一定的误差，并不能让学生心服口服。教材中还有利用“折”与“拼”把三个内角拼成平角的方法，而在实际教学中我们发现：即使提示学生可以用“折”或“拼”来验证，大约也只有四分之一的学生能自主得到有效的折、拼办法，多数学生只会盲目尝试。为此，我们设计了分层智慧学习卡，让学生在学习过程中选择适合自己的学习材料，自主探究三角形内角和，并逐步从操作走向推理，从形象走向抽象，使“面对有差异的学生，实施有差异的教育”成为可能。

【环节一：创设情境，明确目标】

师：今天我们一起来研究三角形的内角和。（出示课题）

师：什么是三角形的内角和？

生：三角形三个内角的度数加起来就是三角形的内角和。

师：你知道三角形的内角和是多少度吗？（大部分同学都认为三角形内角和是180°）

师：三角形的内角和真的是180°吗？这节课我们就一起来研究这个问题。

【环节二：选择支架，自主探究】

1.【活动一】量一量。

（1）独立研究。

师：你们准备怎么研究？

生：画几个三角形，把每个角的度数量出来，再加起来看看是不是180°。

师：这是一种很好的方法，我们确实可以这样来研究。先看一下活动建议。

①从信封里拿出3个三角形（分别是锐角三角形、直角三角形、钝角三角形），量一量每个角的度数。

②填写度数记录表。

度数记录表∠1 ∠2 ∠3 三角形内角和锐角三角形 算式：直角三角形 算式：钝角三角形 算式：

（2）交流研究结果，教师板书求内角和的算式。

师：有不是180°的吗？为什么会出现179°呢？难道三角形内角和除了等于180°，还有其他的可能？

生：量角的时候可能会有误差。

小结：确实量角过程中可能会有误差。那你有没有其他的好办法来验证三角形内角和是180°呢？

2.【活动二】其他方法验证。

（1）出示活动建议：每一位同学都有一个信封，信封内有三角形以及四张“智慧卡”，分别是A、B、C卡和挑战卡。每一张卡上都有一些怎样探索三角形内角和的提示。

①先看智慧A卡，如果有困难，可以看B卡，依次类推。

②结合选择的智慧卡独立研究三角形内角和。如果研究完一张卡还有时间，可以继续研究挑战卡。

③如果还有困难，可以申请和老师一起研究。

【各层次智慧卡】

A卡：信封里有三个三角形，请你剪一剪或拼一拼，验证一个三角形的内角和是180°。

B卡：用信封里的三角形来验证三角形的内角和是180°，有以下两种方法供你选择。

①你可以剪下或撕下三角形的三个角，然后把这三个角拼成一个平角。

②通过折一折的方法，把∠1、∠2、∠3的顶点重合在一起，拼出一个平角。

C卡：①如图所示，你可以像这样剪下或撕下三角形的三个角，把它们的顶点和顶点重合，边与边重合，拼成一个平角。

②如图所示，你能不能继续折，把∠1、∠2、∠3拼在一起，拼成一个平角。

挑战卡：

②借助直角三角形的内角和来研究锐角三角形和钝角三角形的内角和。把你的方法画一画，写一写。

（自主选择合适的智慧卡进行研究）

【环节三：合作交流，补充修正】

1.四人小组交流。

（1）选择C卡的先说，然后按照B、A、挑战卡的顺序进行补充。

（2）把你们发现的求三角形内角和的方法汇总，可以标上序号。

（3）推荐一人准备汇报。

2.小组派代表汇报方法。

（1）方法一：剪、撕拼。

学生上台演示撕下锐角三角形的三个内角拼成一个平角的过程。

师：我们来看一看电脑是不是也是这样拼的。（课件演示撕拼的过程）

师：剩下的直角三角形和钝角三角形你也能这样撕一撕，拼出180°吗？试一试。

师：哪些人拼成功了？课件动态演示另两种三角形的撕拼过程。

小结：我们用剪拼的方法验证了三角形的内角和是180°，还有没有其他的方法呢？

（2）方法二：折一折。

学生上台演示钝角三角形三个角合在一起折出一个平角的过程。

师：我们来看是不是这样。（课件动态演示折拼的过程）

师：剩下的锐角三角形和直角三角形也能像这样折出一个平角吗？试一试。（在学生操作的基础上课件动态演示变化过程）

（3）方法三：数学推理。

师：刚才我们用量、剪拼、折一折的方法验证了三角形的内角和是180°，还有没有其他方法呢？（在学生交流的基础上课件动态演示推理过程）

①验证直角三角形内角和是180°。

课件动态演示：

360°÷2=180°

直角三角形的内角和是180°

②借助“直角三角形内角和是180°”验证锐角三角形和钝角三角形的内角和是180°。

课件动态演示：

3.验证任意三角形的内角和都是 180°。

师：刚才我们用不同的方法验证了这个三角形的内角和是180°。如果是一个任意的三角形，内角和还是180°吗？

课件出示各种不同大小、方位的锐角三角形、直角三角形和钝三角形，演示任意一个三角形都可以分割成两个直角三角形，利用“直角三角形内角和是180°”的结论推理验证。

从课堂实践来看，“分层智慧卡”的使用，给不同层次的学生个性化的帮助，使全体学生都能积极主动参与自主研究过程，提高了课堂教学的有效性。