基于树形结构的铁路车流径路优化模型

温旭红，林柏梁, 陈 雷

(北京交通大学 交通运输学院，北京 100044)

铁路网车流径路分配优化是我国铁路运输一项重要的基础工作，是编制货物运输计划、技术计划、列车编组计划以及列车运行图的基础[1]。我国铁路运输领域的专家学者对铁路车流径路优化进行广泛研究，包括单、多目标的车流径路问题[1-3]，重、空车流的协同车流径路问题[4-5]，铁路车流径路与列车编组计划综合优化[6-7]以及基于多商品网络流思想的车流径路问题[8-10]等。铁路车流有着独特的运行特征，不仅要求同一股车流需要满足不可拆分原则，还要求不同发站车流在某个支点站汇合后，对于具有相同到站的车流视为同一股车流，具有共同的运行径路[11]，即同一到站的车流具有合并式路径。具有这种结构特点的铁路车流径路不仅符合铁路现场组织实际要求，同时也为铁路运输组织工作者制定编组计划创造了良好基础条件。

目前，针对铁路车流的树状径路优化方面的代表性的研究文献有：文献[12]将同一终点的车流合而不分的特点定义为“合并式路径”，并提出了求解合并式路径的多项式启发式算法。文献[13]构建了基于路径集合的铁路车流分配优化模型并通过模拟退火算法进行求解，其中路径集合的确定对模型结果的影响难以忽视。文献[14]将该特点形象地定义为“树形径路”，并在路网规划研究中构建具有树形结构货流分配优化的模型[15]，该模型的约束条件包含高阶非线性项。

本文基于文献[12，14]的相关研究，构建以总走行费用最小为目标函数、满足车流不可拆分和树形径路特点、以弧段上能力限制为约束的铁路车流径路优化的改进模型。

1 树状径路及铁路车流径路优化模型

车流径路方案作为制定编组计划基础必须与改编方案相互匹配。车流径路是由沿途编组去向的径路组合而成[15]，车流的改编中转站必须限制在车流径路上[6]。因此，在车流径路方案中体现为同一终点的车流合而不分的特点。此时，同一终点所有车流的路径呈“树状结构”。结合车流径路和编组计划相关理论，这里把车流径路的树形特点定义为：在支点路网上，有相同到站的技术车流在某支点站汇合后则视为同一股车，具有相同的运行路径直至终点[11]。下面将在由7个技术站构成的简化图(图1)中解释该特点。假设需要对技术车流N17和N27进行分配，路网唯一的瓶颈区段(3,5)的能力为cap(3,5)。

图1 树形径路示意图

当cap(3,5)≥N17+N27时，则车流N17和N27在路网中的运行径路为广义最短路，如图1(a)所示。当cap(3,5)∈[N27,N17+N27)：若不存在树状径路要求，那么两支车流的运输路径如图1(b)所示，即技术车流N17和N27在支点3汇合后分开，并再次相遇于支点6；若满足树状结构要求，那么车流N18和N28在支点站3汇合后不再分开，将共同经过支点4、支点6运输直至终点7，如图1(c)所示。值得注意的是，技术车流也必须满足同一股车流不允许拆分运输的原则。

1.1 模型构建前提和限定

模型的构建主要基于以下假设：

(1)假设已经完成车流以及路网归并[16]，形成了由支点站构成的支点网络；

(2)限定模型应用对象为技术车流在支点路网上的运行径路。

1.2 参数及变量定义

铁路支点网络简化为一个无向图G=(V,E)，其中V为路网的支点站集合，E为路网的弧段集合，且有∀e∈E。对于∀i,j∈V，用Nij表示始发站点i到终到站点j的始发车流量。对于∀i∈V，定义Yi是站点i所有的邻接弧段集合且Yi⊆E；定义Hi为点i的所有邻接点的集合且Hi⊆V。此外，定义Cape为弧段e的通过能力，Le为弧段e的里程。

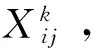
1.3 基于树状结构的铁路车流径路优化模型

大多数情况下，车流径路优化问题多以广义里程最小衡量标准。故本文提出的模型以车流的广义运输里程最小化为目标，以树形径路约束、车流强度守恒约束以及路段能力约束为条件，记为铁路车流径路优化模型M1。

M1：

( 1 )

s.t.

( 2 )

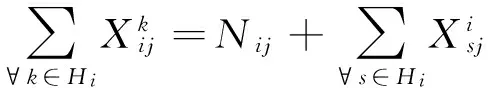
( 3 )

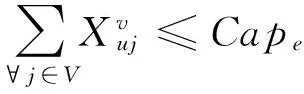
( 4 )

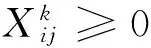
( 5 )

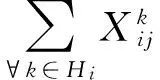
很明显，模型M1中包含非线性约束等式。接下来，将引入0-1辅助变量对模型中非线性约束条件( 2 )进行转化处理。

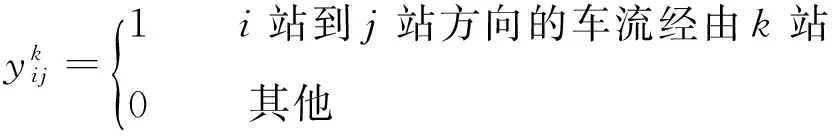
( 6 )

那么，模型M1中约束( 2 )转换为如下形式

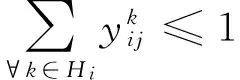
( 7 )

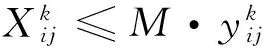
( 8 )

其中，M表示一个足够大的正数。不等式约束( 7 )和( 8 )共同体现了车流径路的树形样式特点。所以，模型M1可以转化为模型M2。

M2：

( 9 )

s.t.

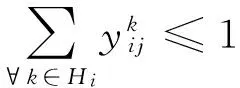
(10)

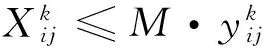
(11)

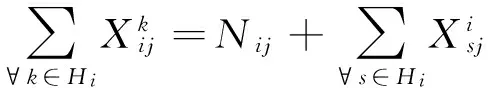
(12)

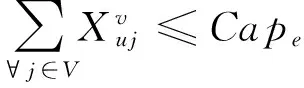
(13)

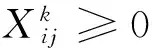
(14)

(15)

显然，模型M2是一个0-1混合整数的单目标数学规划模型，可以通过IBM ILOG CPLEX进行求解验证。

2 算例研究

本文采用文献[8]中路网结构为背景构建了铁路支点路网图(如图2所示)来验证构建的铁路车流径路优化模型的可行性。

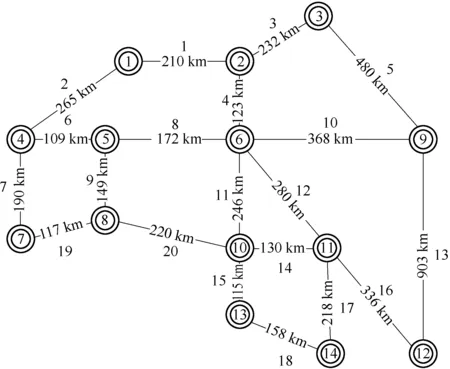
图2 铁路支点路网图

图2中包括20条弧段、14个支点站。假设支点路网中所有路段的上、下行的里程相同，只有序号为4、9和12号的三条路段为瓶颈区段。支点路网的弧段里程以及瓶颈区段通过能力参数见表1。另外，为了全面验证模型的树状径路效果，表1中设置了3组不同的瓶颈区段能力限制数据。

表1 支点路网的弧段里程和弧段能力参数

注：“—”表示路段的通过能力不受限制。

基于以上假设和数据，在处理器为Intel Core i3、内存为6 G的计算机上通过MATLAB 2012a编程语言调用IBM ILOG CPLEX 12.6优化软件对所构建铁路车流径路优化模型M2进行验证。验证采用21支模拟车流OD数据。三组不同能力参数下模型径路优化结果见表2。

表2 不同路段能力参数下的车流径路优化结果

由表2可以看出，在三组不同的弧段能力数据下终到点为①、⑨和的车流路径发生了调整，详细车流径路变化对比如图3所示。

图3(a)和3(b)为终到点为①的两支车流N10,1和N12,1的径路变化对比图。在第2和3组能力限制下这两支车流的径路相同，均在支点②汇合后直到终点，如图3(b)所示。而在第1组能力数据下，车流N12,1径路调整为12→9→6→2→1，与车流N10,1在支点⑥汇合后直到终点①，如图3(a)所示。

图3(c)和3(d)为终到点为⑨的三支车流N4,9、N7,9和N8,9径路变化对比图。在第1、2组能力数据下这三支车流在支点⑥相汇后直到终点，如图3(c)所示。在第3组能力数据下，N7,9和N8,9的车流径路不变而车流N4,9径路调整为4→1→2→3→9，如图3(d)所示。

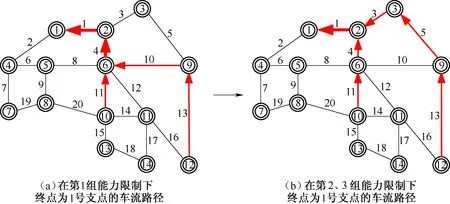
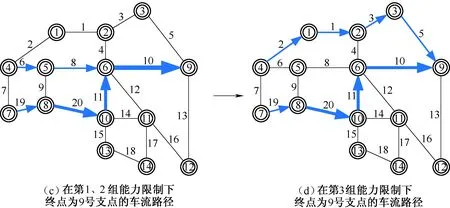
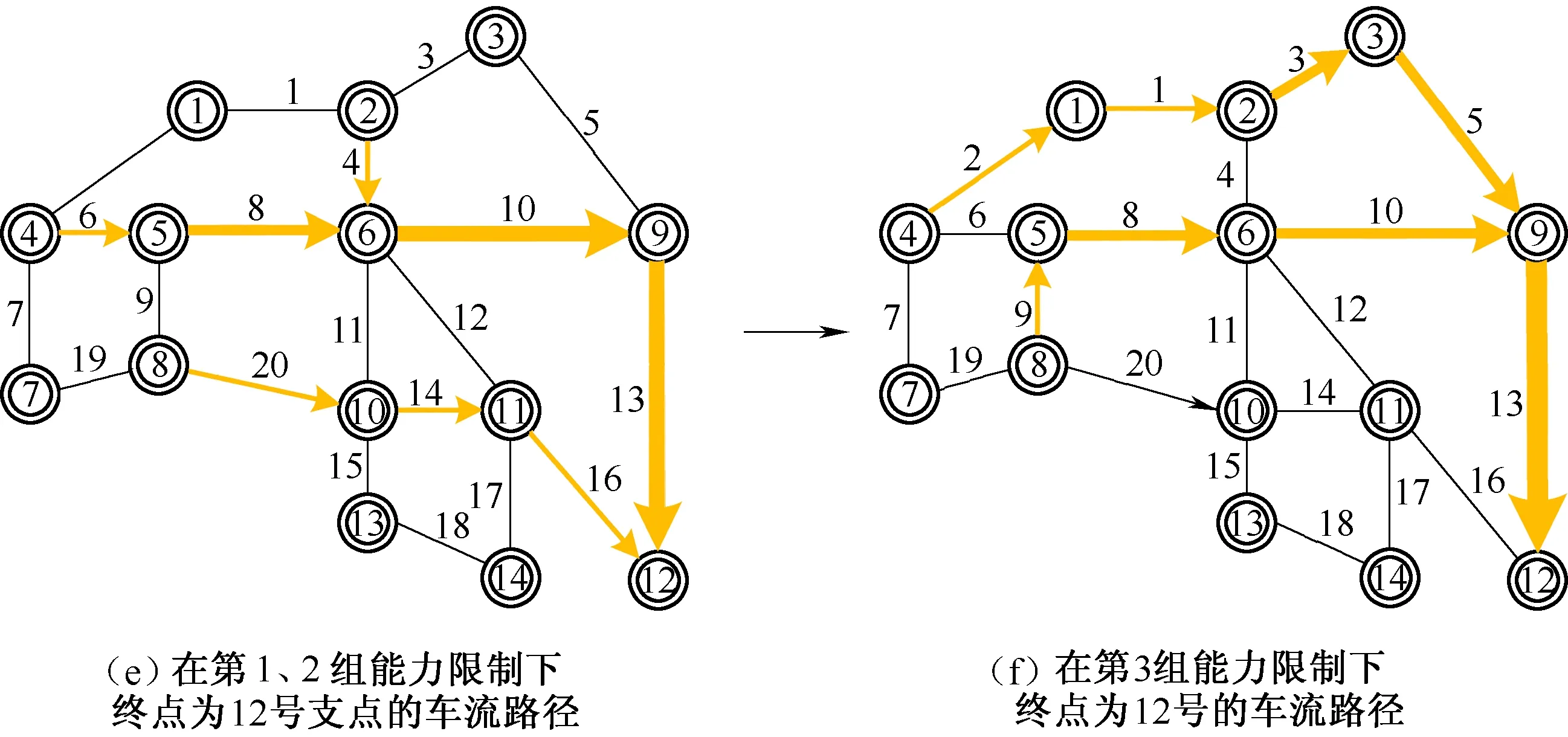
图3 在不同能力限制下车流径路变化对比

由图3可以明显发现，虽然受到弧段能力参数变化的影响车流径路产生变化，但是模型仍可以保证得到车流径路具有树状结构特征。

在第1组能力参数下与文献[8]中模型优化的路径结果对比见表3。

表3 车流径路优化结果对比

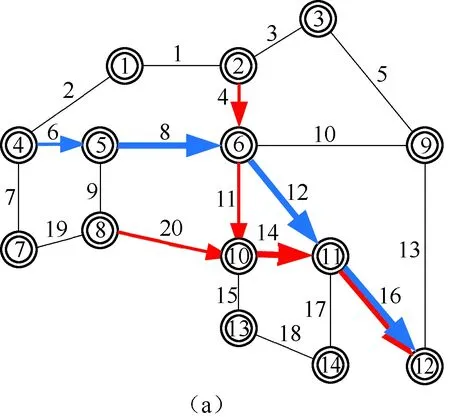
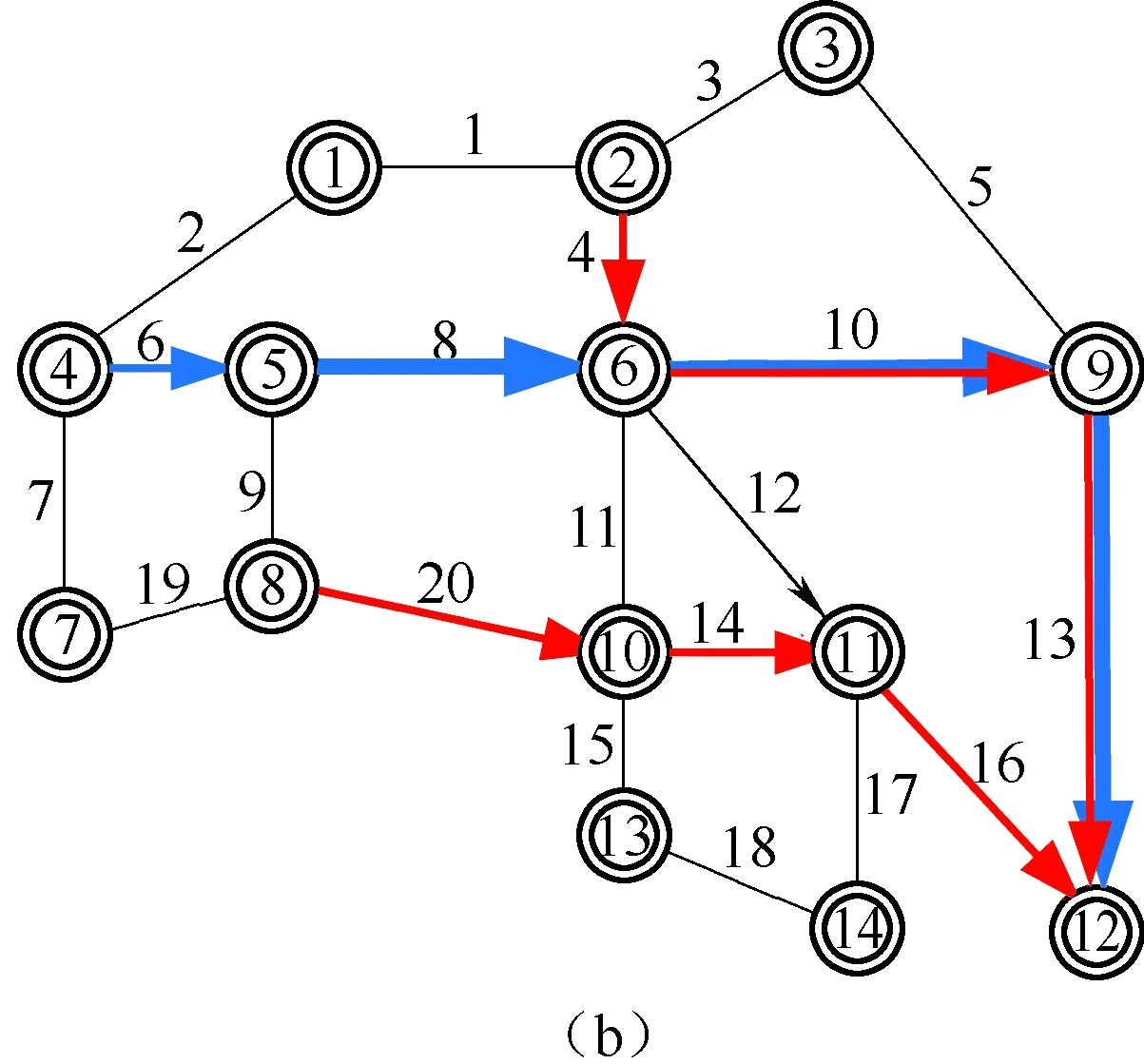
图4 终点到12的车流径路优化对比

3 结论及展望

本文根据我国铁路车流独特的运行特征，提出了具有树状结构的铁路车流径路优化模型。模型以传统车流总走行里程最小为优化目标，约束条件包括车流径路的树状结构特点、车流强度守恒以及弧段通过能力限制。研究表明：本文提出的模型可以保证不同的弧段能力参数下优化的车流路径都具有树状结构；与传统优化模型对比，构建的模型可以满足铁路车流径路的树状结构要求。

铁路网车流优化是NP难问题，优化软件难以解决大规模问题。接下来的研究重点是大规模铁路网下模型求解算法研究。另外，车流径路与编组计划关系密切，与编组计划的综合优化也是未来研究的重要方向。

参考文献：

[1]高旭敏, 周潮, 顾炎. 铁路网货车车流经路分配的优化模型及算法[J]. 铁道学报, 1992, 14(4): 43-48.

GAO Xumin, ZHOU Chao, GU Yan. The Optimization Model and Algorithm of the Distribution of Cars' Paths in a Railway Network[J]. Journal of the China Railway Society, 1992, 14(4):43-48.

[2]施其洲. 铁路网络系统运输能力与车流路径模型[J]. 铁道学报, 1996, 18(4): 1-9.

SHI Qizhou. Models for Rail Network System Transportation Capacity and Traffic Pathing[J]. Journal of the China Railway Society, 1996, 18(4): 1-9.

[3]孙晚华，郑时德. 铁路车流径路优化算法的研究[J];北方交通大学学报, 1995, 19(1): 39-44.

SUN Wanhua, ZHENG Shide. Study on the Optimization Algorithm of Railway Wagon Flow Path [J]. Journal of Northern Jiaotong University, 1995, 19(1): 39-44.

[4]施其洲, 施勇. 具有双向空重车流的路网车流径路多目标线性规划模型及算例[J]. 铁道学报, 1999, 21(1): 1-9.

SHI Qizhou, SHI Yong. Multi-objective Linear-programming Model and Its Algorithm for Car Flow Routing with Bidirectional Heavy and Empty Cars in Railway Network[J]. Journal of the China Railway Society, 1999, 21(1): 1-9.

[5]杜进有, 姚新胜, 黄洪钟. 路网车流径路的满意优化[J]. 系统工程, 2006, 23(9): 46-49.

DU Jinyou, YAO Xinsheng, HUANG Hongzhong. Satisfactory Optimization of the Wagon Flow Problem in Railway Network[J]. Systerm Engineering, 2006, 23(9): 46-49.

[6]史峰, 孔庆钤, 胡安州. 车流径路与编组计划综合优化的网络方法[J]. 铁道学报, 1997, 19(1): 1-6.

SHI Feng, KONF Qingqian, HU Anzhou. A Network Method of Comprehensive Optimization of Wagon Path and Train Formation Plan[J]. Journal of the China Railway Society, 1997, 19(1): 1-6.

[7]林柏梁, 朱松年. 路网上车流径路与列车编组计划的整体优化[J]. 铁道学报, 1996, 18(1): 1-7.

LIN Boliang, ZHU Songnian. Synthetic Optimization of Train Routing and Makeup Plan in a Railway Network[J]. Journal of the China Railway Society, 1996, 18(1): 1-7.

[8]纪丽君,林柏梁,乔国会,等.基于多商品流模型的铁路网车流分配和径路优化模型[J]. 中国铁道科学, 2011, 32(3): 107-110.

JI Lijun, LIN Boliang, QIAO Guohui, et al. Car Flow Assignment and Routing Optimization Model of Railway Network Based on Multi-commodity Flow Model[J]. China Railway Science, 2011, 32(3):107-110.

[9] 田亚明, 林柏梁, 纪丽君. 基于多商品里和虚拟弧的铁路车流分配点-弧和弧-路模型研究[J].铁道学报,2011, 33(4): 7-12.

TAN Yaming, LIN Boliang, JI Lijun. Railway Car Flow Distribution Node arc and Arc-path Models Based on Multi-commodity and Virtual Arc[J]. Journal of the China Railway Society, 2011, 33 (4):7-12

[10] 温旭红, 林柏梁, 王龙, 等. 基于多商品网络流理论的铁路车流分配及径路优化模型[J]. 北京交通大学学报, 2013, 37(3): 117-121.

WEN Xuhong, LIN Boliang, WANG Long, et al. Optimization Model for Railway Car Flow Assignment and Routing Plan Based on Multi-commodity Network Flow theory[J]. Journal of Beijing Jiaotong University, 2013, 37(3): 117-121.

[11]林柏梁, 徐忠义, 黄民, 等. 路网发展规划模型[J]. 铁道学报, 2002, 24(2): 1-6.

LIN Boliang, XU Zhongyi, HUANG Min, et al. An Optimization Model to Railroad Network Designing [J]. Journal of the China Railway Society, 2002, 24(2):1-6.

[12]史峰, 李致中. 铁路车流路径的优选算法[J]. 铁道学报, 1993, 15(3): 70-76.

SHI Feng, LI Zhizhong. An Algorithm for the Wagon Path Problem[J]. Journal of the China Railway Society, 1993, 15(3): 70-76.

[13]史峰, 黎新华, 莫辉辉, 等. 铁路OD分配优化方法[J]. 中国铁道科学, 2004, 25(4): 116-119.

SHI Feng, LI Xinhua, MO Huihui, et al. An Optimal Method for Railway Origin Destination Assignment[J]. China Railway Science, 2004, 25(4): 116-119.

[14]LIN B L. A Tree-type Car Route Guidance Models for ITS[C]//Kelvin Wang,Guiping Xiao, Lei Nie, et al. Traffic and Transportation Studies(2002).American Society of Civil Engineers,2002:620-625.

[15]李宵寅. 基于不确定参数的列车编组计划与车流径路综合优化研究[D]. 成都：西南交通大学, 2011.

[16]胡思继. 铁路行程组织[M].北京：中国铁道出版社，2012:114-116.