新建盾构隧道近接施工对既有隧道纵向变形影响研究

卢岱岳，王士民，何 川，夏 鑫

(西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031)

近年来，我国城市交通基础设施投资逐步加大，城市地下交通建设发展较快。城市地铁隧道多采用盾构法修筑，随着地下空间开挖深度、密度的增大，两条或多条隧道近距离施工的情况日益增多。新建隧道施工会对周围土体产生扰动，引起既有隧道结构形变，过大的变形可能导致既有隧道结构及附属设施难以满足营运要求，严重时可能造成运营安全事故，甚至会危及结构安全。

隧道近接施工对既有隧道影响的现有研究，可分为数值模拟和解析法两类，且以前者为主。文献[1-4]分别通过有限元软件模拟分析盾构施工对既有隧道应力和衬砌变形的影响。对于新建隧道施工力学行为影响解析方法的研究，部分学者将其简化为平面应变状态下的双洞开挖问题求解。文献[5]针对无限介质中两个等尺寸圆孔应力场，通过双调和函数法获得其精确解。文献[6]采用双极坐标推导平行隧道的应力场解析解。文献[7]结合复变函数理论和交替法重复循环计算步骤，得到半无限平面内双孔平行圆形隧道开挖问题的弹性解。但是近接施工中两个隧道是一种具有时空效应的三维立体交叉关系，上述研究难以合理反映新建隧道-扰动土体-既有隧道三者整体的空间力学特性。

因此，部分学者开始探索隧道近接施工三维解析解的研究工作。文献[8]基于Winkler地基梁理论，分析新建隧道施工对上方隧道的影响。文献[9]从应力迁移角度出发，针对外力作用下衬砌和土体两种不同介质耦合作用时应力的快速迁移现象，构建了考虑土体流变特性的盾构近接施工应力迁移模型，得到应力迁移解析式。文献[10]基于Kerr地基梁理论，考虑地层损失率、荷载形状参数和抗弯刚度等因素，建立了计算新建隧道施工对上方既有隧道影响的解析方法。

新建盾构隧道掘进过程中盾构与地层之间的相互作用，包括土仓压力控制、盾体侧面摩阻力及盾尾土体损失等因素，均直接影响盾构施工对周围地层的扰动程度，既有文献对上述因素尚无较深入研究。因此，本文考虑盾构施工过程中的动态影响因素，推导盾构隧道施工引起周围土体位移的解析表达式，建立扰动土体位移与既有隧道的映射关系，得到既有隧道因新建隧道施工产生的附加位移。针对平行、正交以及重叠三种不同形式的盾构隧道近接施工，应用本文理论分析方法计算，将计算结果与数值模拟结果对比验证。

1 新建盾构隧道施工对既有盾构隧道纵向变形影响分析

盾构施工对既有隧道的影响通过周围土体传递，因此，新建盾构隧道施工对既有隧道变形的影响研究，应在分析盾构施工对周围土体位移场和应力场影响[11-12]的基础上，探讨扰动土体位移场、应力场对既有隧道的影响。采用两阶段方法[13]分析盾构施工对既有隧道的影响。第一阶段计算盾构施工引起既有隧道位置处土体的自由位移场，第二阶段基于某地基模型将既有隧道视为无限长梁，将所得土体自有位移场施加于既有隧道。通过建立既有隧道的受荷变形平衡微分方程，得到既有隧道因盾构施工产生的内力和位移。两阶段方法适用于软土均匀地层中沿直线掘进的盾构施工相互影响分析。盾构隧道施工导致土体产生移动的因素，在施工期间主要是盾构正面附加推力、盾体侧壁摩擦力和盾尾土体损失。

1.1 盾构正面附加推力和侧壁摩擦力对周围地层的扰动

基本假定：土体为均匀的半无限弹性体；不考虑土体排水固结，仅考虑盾构施工期间的影响；假定盾构机在正常固结软土中沿直线掘进，不考虑纠偏和注浆压力的影响，盾构机掘进仅是空间位置上的变化，与时间无关。

盾构施工过程中，为保证开挖面前方及上方土体稳定，尽量降低掘进对周围环境的影响，作用在掌子面上的顶进压力通常要略大于掌子面静止土压力。盾构机正面推力与静止土压力之差即为正面附加推力，实际工程中该值一般为水平侧向压力的0.1倍。本次盾构正面附加压力简化为圆形均布荷载p，应用Mindlin[14]解对整个圆形工作面进行积分可得到既有隧道轴线上任意一点的位移，如图1所示。

图1 盾构施工扰动理论分析模型

Mindlin位移解：在匀质各向同性弹性半无限体中，地面以下H深度作用一水平集中荷载p所产生的土体任意点(x，y，z)的y、z方向位移为

(1)

(2)

对盾构工作面附加荷载积分后，土体中任意一点的y、z方向位移计算公式为

(3)

(4)

盾构侧壁摩擦力简化为沿盾体表面的均布荷载q，应用Mindlin解对整个盾体圆柱表面积分即可得到既有隧道轴线上任意一点的位移，如图1所示。

对盾体侧壁摩擦力进行积分后，土体中任意一点的y、z方向位移计算公式为

(5)

(6)

式中：

1.2 盾尾土体损失对周围地层的扰动

土体损失是指实际开挖土体体积大于设计开挖土体体积的数量， 隧道周围土体会移动来填补这部分空隙体积。关于这个问题的求解，应用解析方法较多的是文献[15，16]的方法，该方法基于如下假定：土体为线弹性材料，处于软土地区非排水条件下；基于均匀半弹性二维平面，采用椭圆形土体移动平面，如图2所示；采用等效间隙参数g定义等量不排水土体损失率ε0。

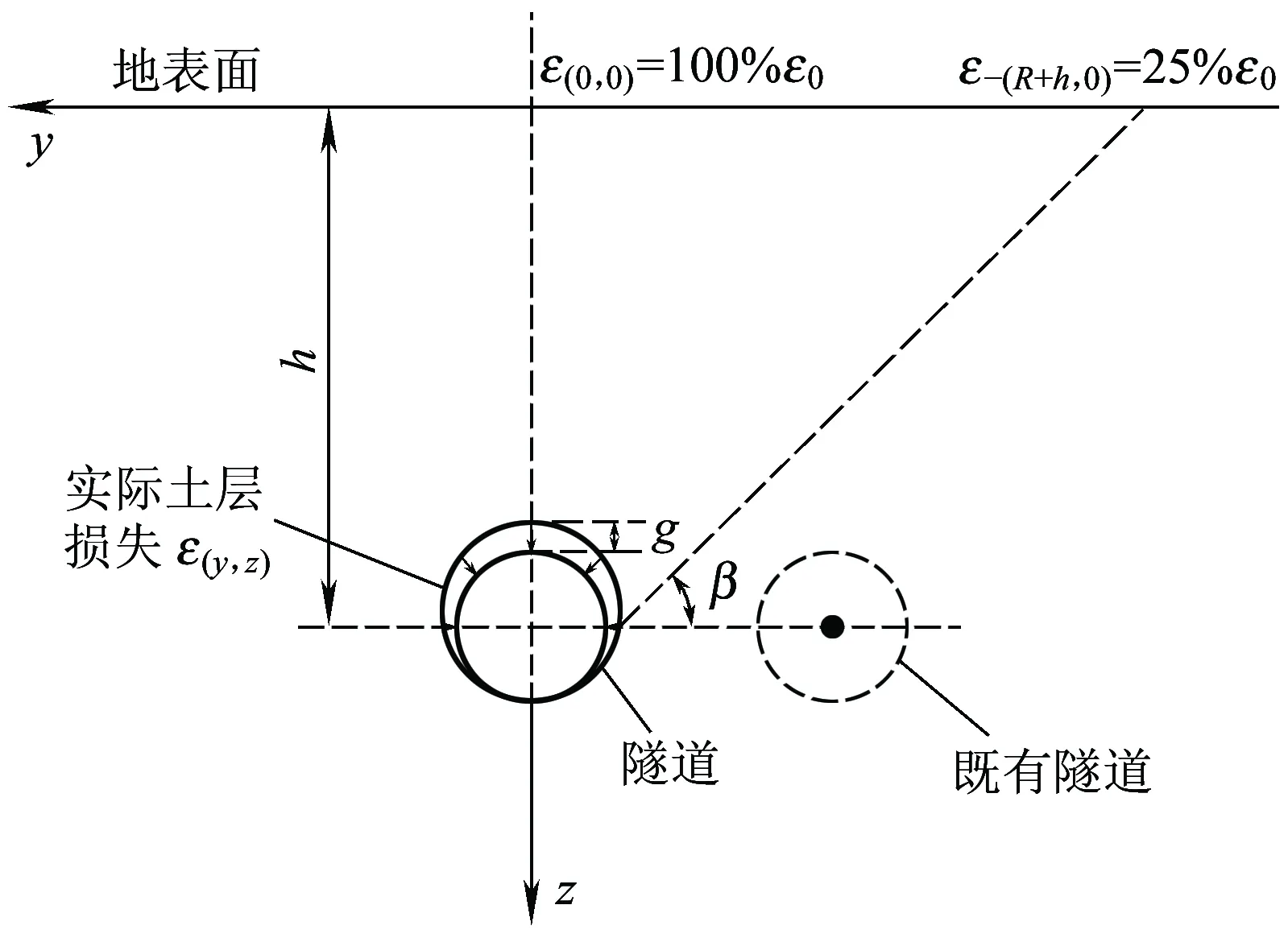
图2 土体损失产生的变形模式

土体损失导致土体三维空间内y、z方向的位移计算公式为

(7)

(8)

1.3 扰动土体对既有隧道附加位移的影响

针对上述影响土体位移的三个主要因素，即盾构正面附加推力、盾构侧壁摩擦力、盾尾土体损失，基于开挖面坐标系将式(3)、式(5)、式(7)位移解进行累加可得到受扰动土体y方向位移表达式(9)。将式(4)、式(6)、式(8)位移解进行累加可得到受扰动土体z方向位移表达式(10)。

(9)

(10)

将土体的扰动位移施加于既有隧道，并基于图3所示的Pasternak地基模型[17]建立既有隧道受荷变形平衡微分方程，得到其变形和内力。

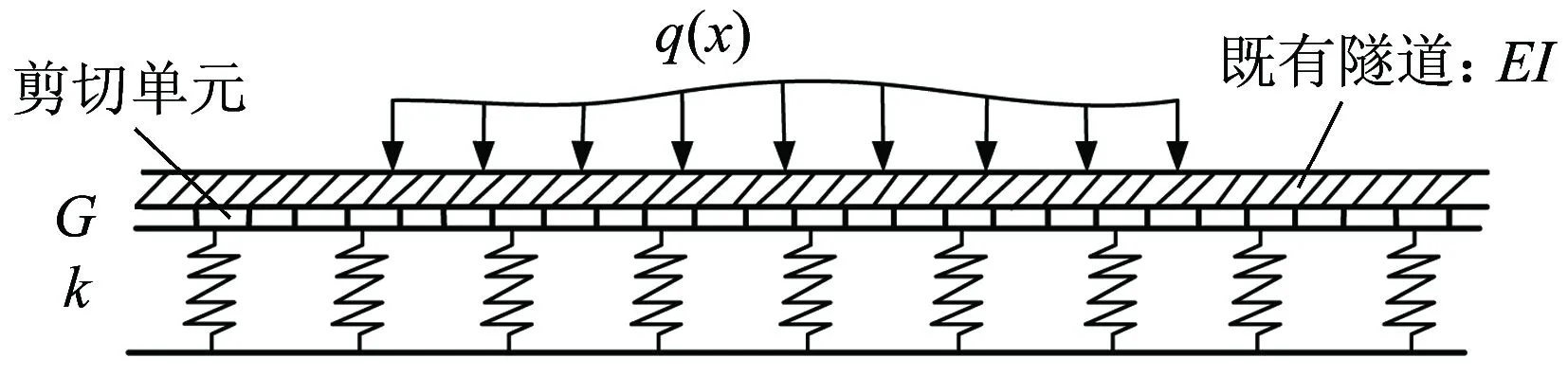
图3 Pasternak地基模型示意

Pasternak地基模型的基本假定为：土体与隧道均为连续均质弹性体；管线存在不影响隧道开挖；隧道存在不影响管线轴线处土体受力响应；管线与周围土体始终保持接触。

图3中，q(x)为作用在既有隧道上的土体附加应力，该附加应力可由第一阶段的土体扰动位移进行计算；EI为既有隧道刚度(考虑隧道纵向接缝折减后刚度)；G为地基剪切刚度；k为地基弹簧刚度[18]；既有隧道直径为D。

根据Pasternak地基模型，由土体自由位移场导致的作用在既有隧道上的附加荷载为

(11)

既有隧道在上述附加荷载qy(x)作用下会产生y方向的挠度变形wy(x)，因该扰度变形wy(x)导致的作用在既有隧道上的土体弹簧附加荷载为

(12)

在上述两个附加荷载作用下，既有隧道受荷的平衡微分方程为

(13)

将式(10)代入式(11)整理可得到既有隧道标准受荷平衡微分方程为

(14)

首先求出集中荷载P作用下微分方程的解为

(15)

既有隧道上任意一点ξ所受附加荷载为qy(ξ)dξ，隧道轴线上任意一点x的y方向位移dwy(x)为

αsinβ|x-ξ|)dξ

(16)

对既有隧道轴线上一定范围内的附加荷载积分，得到既有隧道某一点x位置的y方向变形wy(x)为

(17)

同理，既有隧道某一点x位置的z方向变形wz(x)为

(18)

地下空间中的任意两条隧道，采用式(17)和式(18)进行相应位移换算即可得到既有隧道的变形。

2 工程实例验证

针对平行、正交下穿及重叠(新建隧道与既有隧道上下并行布置)三种不同近接情况，分别结合具体工程实例，应用本文提出的解析解对既有隧道因新建隧道扰动产生的附加位移进行分析，结合现场实测数据及数值模拟分析结果，比较分析其正确性和准确性。

2.1 平行新建盾构隧道施工对既有盾构隧道的影响

依托某地下通道工程，采用理论公式和数值模拟对盾构隧道的施工影响进行分析，求解新建盾构隧道施工引起既有隧道附加位移，并将数值计算得到的沉降值与现场实测值比对，验证所推导解析解的正确性。

2.1.1 工程概况

该工程由南北两条地下通道构成，全长约2 540 m。整个工程由地面道路、明挖敞开和暗埋段、明挖盾构井以及地下隧道组成。本工程采用泥水平衡盾构机进行施工，该盾构机外径13.2 m，壁厚0.2 m，总长12.4 m，盾构机总重1 120 t。盾构段采用预制管片单层衬砌，管片环为9等分块，管片环外径12.8 m，管片厚度0.5 m，管片环宽度2 m。两条隧道净距9 m，两隧道中心线埋深均为16 m，其平面布置如图4所示。

2.1.2 施工扰动对既有隧道影响的解析解

针对盾构正面附加推力、侧壁摩擦力以及盾尾土体损失，采用上述公式并通过数值积分求解既有隧道轴线上土体受扰动后的位移。本次采用图1中的坐标系进行计算，本工程p=30 kPa，q=50 kPa，h=16 m，D=12.4 m，L=12.8 m，ε0=0.48%，g=0.026 4 m。土体参数加权平均后G=1.5 MPa，μ=0.31。应用式(3)、式(5)、式(7)可求出既有隧道轴线上土体受扰动后y方向的位移变化。

基于Pasternak地基模型，将盾构施工产生的土体自由位移转化为作用在既有隧道上的附加荷载，得到既有隧道受荷的平衡微分方程。针对开挖面前后120 m范围内的土体位移，通过式(11)、式(14)和式(17)对既有隧道任意一点的侧向位移进行求解，得出既有隧道因盾构施工产生的侧向水平附加位移。

2.1.3 有限元数值模型

本工况采用ABAQUS 6.10软件建立模型，并在分析过程中采用弹性介质模拟土体。隧道管片、盾体以及注浆体的材料较均匀且刚度较大，均选用线弹性本构模型。本次数值模拟采用三维建模，所有部件都采用实体建模，具体参数及单元类型见表1。

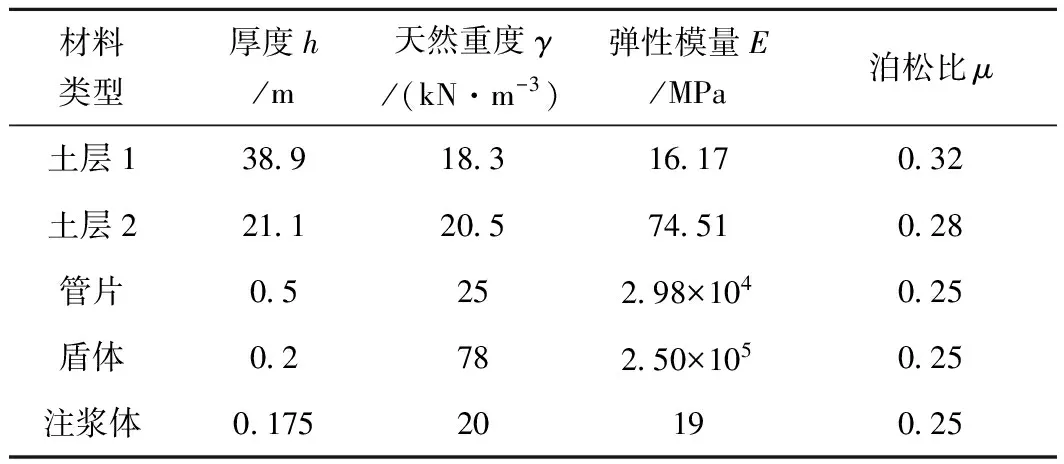
表1 材料参数及单元类型

考虑到两隧道埋深、间距以及有限元离散误差和计算误差，计算范围一般选取沿洞径各个方向均不小于3～4倍洞径[19]，故本次数值模型确定为200 m×100 m×70 m，如图5所示。该模型共计227 800个单元，251 928个节点。

图5 双线平行隧道数值模型

盾构施工是动态连续的过程，本文采用数值软件分步开挖方法模拟这一过程[20]，如图6所示。

图6 模拟盾构开挖过程示意

2.1.4 结果分析

图7为平行新建隧道盾构施工引起既有隧道土体扰动位移曲线。从图7可以看出，盾构施工对周围地层的扰动以盾构侧壁摩擦力为主，其中盾构侧壁摩擦力、盾构正面附加推力和盾尾土体损失的影响分别占85%、12%和3%。盾构正面附加推力、盾构侧壁摩擦力引起的土体扰动位移沿既有隧道轴线均呈现以掌子面为界的反对称分布形态，即掌子面前方地层受压，产生移向新建隧道方向的附加位移，掌子面后方地层受拉，产生背离新建隧道方向的附加位移。在距掌子面11 m处，土体水平侧向位移分别达到最大值，位移方向相反；随着与开挖面距离的增大其产生的土体扰动位移逐渐减小，超过100 m范围后其影响可忽略。同时，盾尾土体损失引起的土体扰动位移，沿既有隧道轴线负向，在开挖面后方逐渐增大，在约30 m后趋于稳定；在开挖面前方其影响可忽略。

注：“+”代表移向在建隧道；“-”代表背离在建隧道

图7 盾构施工导致土体y方向位移

图8为解析解得出的既有隧道因盾构施工产生的侧向水平位移变形曲线。既有隧道轴线产生的侧向变形同周围土体的水平侧向位移变形趋势一致，在距盾构11 m处分别达到极值，因此对于平行隧道近接施工而言，施工中应该重点关注盾构侧壁摩擦这一影响因素。两种方法计算结果吻合较好，开挖面前后土体及既有隧道变形趋势一致，但由于数值模拟未考虑开挖过程中的土体损失，同时考虑了开挖应力释放、注浆压力及顶推力对控制土体变形的影响，因此，由图8可以看出，数值解在峰值处较解析解小。

注：在建隧道盾构开挖面位于坐标0位置；“+”代表移向在建隧道；“-”代表背离在建隧道。

图8 既有隧道轴线水平位移的理论分析和数值模拟结果

图9为盾构掘进过程中地表横向沉降的发展变化情况。随着南线盾构的掘进，地表沉降槽以南线隧道为轴线左右对称，同时在影响范围和深度上逐渐增大，当北线盾构隧道开始掘进后，地表沉降逐渐扩展到北线隧道上方并产生两个峰值点，两个峰值点分别位于南线和北线隧道轴线上，沉降值分别为19.2 mm、17.1 mm。

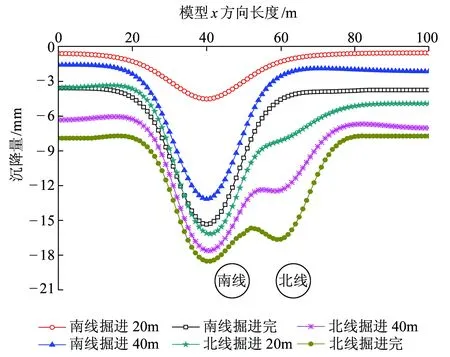
图9 数值模拟地表沉降槽变化

通过数值模拟和施工监测得到南线盾构施工完成和北线盾构施工完成后的地表沉降，如图10所示。南线盾构施工完成后，数值模拟和施工监测都得到单峰地表沉降曲线，数值模拟结果比实测结果略大，二者的整体变形趋势一致。随着北线盾构施工的完成，数值模拟和实测数据都得到双峰的地表沉降曲线，并且最终沉降槽的两个峰值点分别位于南线和北线隧道轴线上。

图10 地表沉降的数值模拟与实测结果对比

2.2 正交新建盾构隧道施工对既有隧道的影响

选取西安地铁某区间，采用ANSYS 11.0软件模拟分析新建盾构隧道从既有盾构隧道下方正交穿过时对既有隧道的影响，模型如图11所示。新老隧道管片衬砌的外径均为6 m，内径均为5.4 m，管片厚30 cm，管片幅宽为1.5 m。模型长80 m，宽80 m，高45 m。既有隧道埋深6 m，新建隧道距既有隧道1D距离，埋深18 m。

图11 双线正交隧道数值模型

针对盾构正面附加推力、侧壁摩擦力以及盾尾土体损失，采用理论公式求解得到既有隧道轴线上土体受扰动后的竖直方向位移。计算结果如图12、图13所示。

注：“+”代表向下移动；“-”代表向上移动。

图12 盾构施工导致土体竖直方向位移

图13 既有隧道轴线竖向位移的理论分析和数值模拟结果

正交新建隧道盾构施工对上方土体竖直方向附加位移的影响程度不同，如图12所示。当新建隧道掌子面恰好位于既有隧道轴线下方时，盾尾土体损失成为主要因素，盾尾土体损失、盾构侧壁摩擦力和盾构正面附加推力影响程度分别占64%、36%和0%。盾构侧壁摩擦力的作用与盾尾土体损失相反，其在掌子面正上方土体中产生压力，形成竖直向上的附加位移，上述因素引起的附加位移均沿既有隧道轴线向两侧迅速减小，在30 m范围内影响变化较明显。因此对于正交盾构隧道近接施工而言，施工中应重点控制盾尾土体损失。

通过数值模拟和解析求解得到正交隧道盾构近接施工引起的既有隧道竖向位移曲线，如图13所示。由图13可以看出，盾构施工沿轴线在交汇区域前后38 m范围内对既有隧道产生影响。解析解与数值解的变化趋势一致，且幅值较接近，进一步验证了解析解的正确性。

2.3 重叠新建盾构隧道施工对既有隧道的影响

选取与2.2节相同工程地质情况，采用ANSYS 11.0软件模拟分析新建盾构隧道从既有盾构隧道正下方平行穿过时对既有隧道的影响，模型如图14所示。新老隧道管片衬砌的外径均为6 m，内径均为5.4 m，管片厚30 cm，管片幅宽为1.5 m。模型长160 m，宽80 m，高45 m。既有隧道埋深6 m，新建隧道距既有隧道1D距离，埋深18 m。

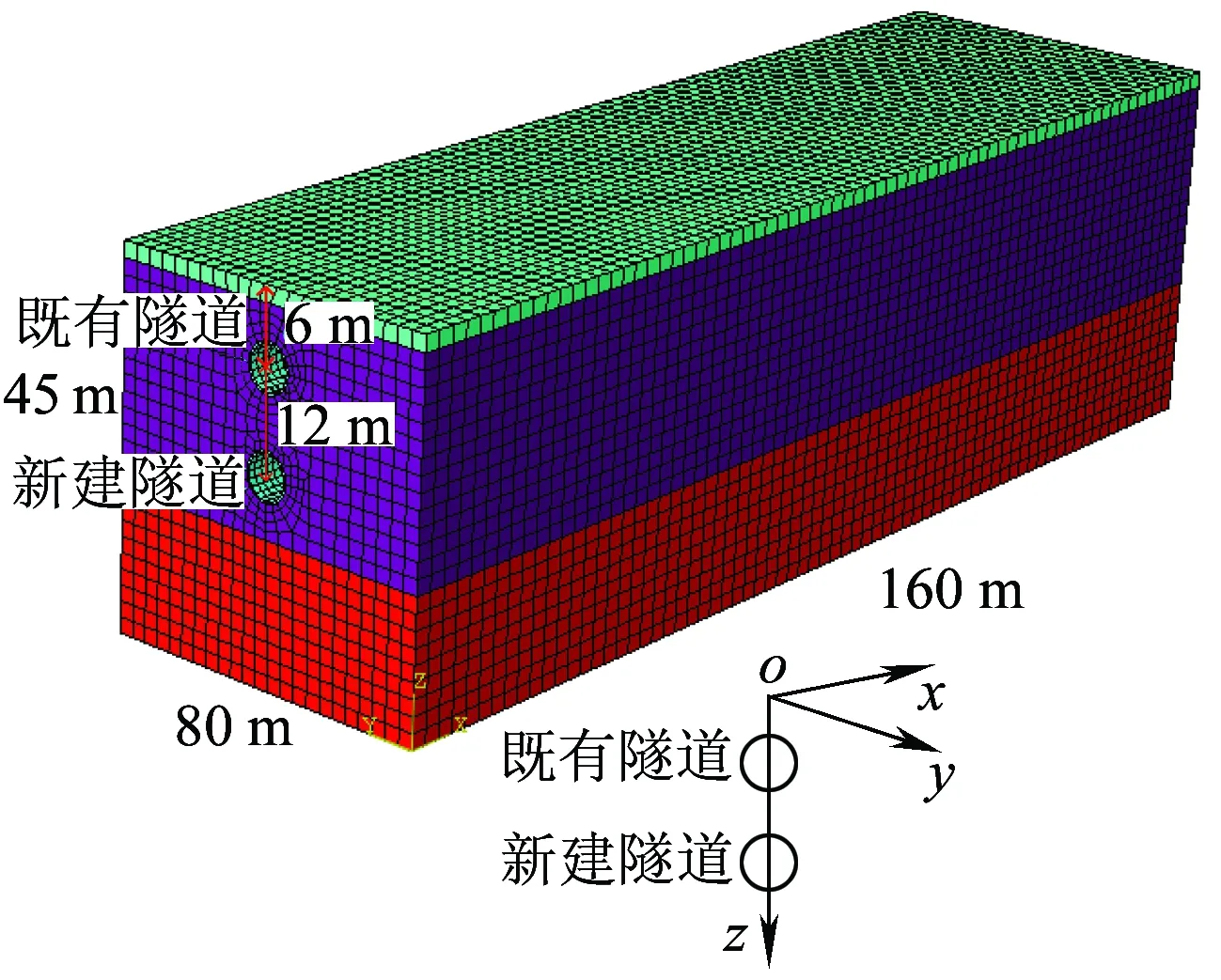
图14 双线重叠隧道数值模型

针对盾构正面附加推力、侧壁摩擦力以及盾尾土体损失，采用理论公式经求解得到既有隧道轴线上土体受扰动后的竖直方向位移。计算结果如图15、图16所示。

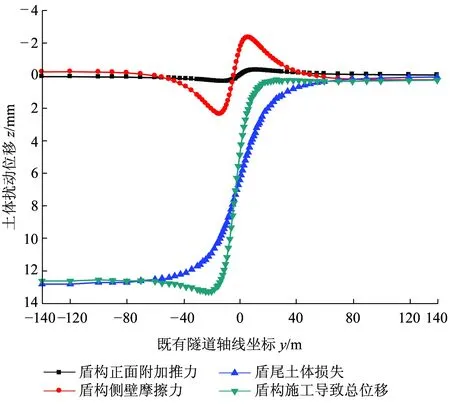
注：“+”代表向下移动；“-”代表向上移动。图15 盾构施工导致土体z方向位移

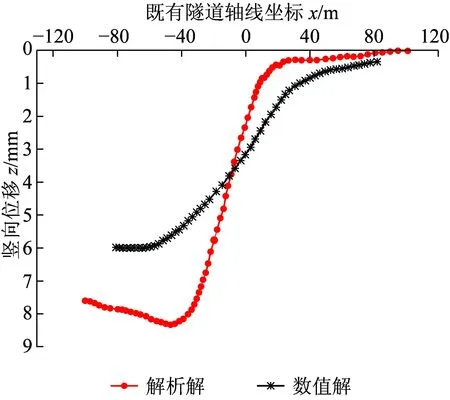
图16 既有隧道轴线竖向位移的理论分析和数值模拟结果

重叠新建隧道盾构近接施工过程中各影响因素对上方土体竖直方向位移的影响程度不同，盾尾土体损失影响最大，盾尾土体损失、盾构侧壁摩擦力和盾构正面附加推力的影响分别占86%、11%和3%。盾构正面附加推力、盾构侧壁摩擦力引起的土体扰动位移沿既有隧道轴线均呈现以掌子面为界的反对称分布形态，即掌子面前方地层受压，产生竖直向上的附加位移，掌子面后方地层受拉，产生竖直向下的附加位移。在距掌子面11 m处，土体竖向位移达到最大值，随着与开挖面距离的增大其产生的土体位移逐渐减小，超过50 m范围后其影响可忽略。同时，盾尾土体损失引起的土体扰动位移，沿既有隧道轴线负向逐渐增大，在掌子面后方约40 m处趋于稳定，在掌子面前方则逐渐减小。因此对于重叠隧道盾构近接施工而言，施工中同样应重点控制盾尾土体损失。

通过数值模拟和解析求解得到的重叠隧道盾构近接施工引起的既有隧道竖向位移曲线，如图16所示。由图16可以看出，盾构施工沿轴线在掌子面前方20 m、后方40 m范围内对既有隧道产生较大影响。解析解与数值解的变化趋势一致，两种方法的计算结果在盾尾后方有一定差异，原因在于数值分析求解通过注浆压力以及管片拼装等过程限制土体变形，而解析解的盾尾土体损失对于其后一定范围土体的竖向位移影响较大。在开挖面及盾尾周围一定范围内的土体变形和大小具有较好的相似性，在一定程度上验证了解析解的正确性。

3 结论

(1)基于Mindlin解和Loganathan公式对盾构施工正面附加荷载、侧壁摩擦力及盾尾土体损失的作用进行数值积分求解，得出既有隧道轴线位置处土体的竖向和侧向自由位移场的计算表达式。

(2)将盾构施工正面附加荷载、侧壁摩擦力及盾尾土体损失等因素引起的土体扰动总位移施加于既有隧道，借助Pasternak地基模型建立既有隧道受荷变形平衡微分方程，得到既有隧道任意位置的附加位移表达式。

(3)针对平行、正交以及重叠三种近接形式的隧道工程实例，借助本文推导的解析解得到不同近接施工情况下既有隧道的纵向变形曲线，结果表明盾构侧壁摩擦力是平行盾构隧道近接施工过程中的主要影响因素，对于正交和重叠双线盾构隧道而言，盾尾土体损失是主要影响因素。将解析解与数值模拟、实测结果进行对比分析发现，三者整体上具有较好的吻合性，验证了建立的新建盾构隧道对既有隧道纵向变形理论分析方法的正确性。

参考文献：

[1]李磊,张孟喜,吴惠明,等.近距离多线叠交盾构施工对既有隧道变形的影响研究[J].岩土工程学报,2014,36(6):1 036-1 043.

LI Lei,ZHANG Mengxi,WU Huiming,et al.Influence of Short-distance Multi-line Overlapped Shield Tunnelling on Deformation of Existing Tunnels[J].Chinese Journal of Geotechnical Engineering,2014,36(6):1 036-1 043.

[2]毕继红,江志峰,常斌.近距离地铁施工的有限元数值模拟[J].岩土力学,2005,26(2):277-281.

BI Jihong,JIANG Zhifeng,CHANG Bin.Numerical Simulation for Constructions of Metro Tunnels with Short Distance Between Them[J].Rock and Soil Mechanics,2005,26(2):277-281.

[3]姜忻良,贾勇,王涛.近距离平行隧道盾构施工对老隧道影响的数值模拟[J].天津大学学报,2007(7):30-34.

JIANG Xinliang,JIA Yong,WANG Tao.Numerical Simulation of Influence of Shield Tunneling on Short Distance Parallel Existing Tunnel[J].Journal of Tianjin University,2007(7):30-34.

[4]DO N A,DIAS D,ORESTE P P.Three-dimensional Numerical Simulation of Mechanized Twin Stacked Tunnels in Soft Ground[J].Tunnelling and Underground Space Technology,2014,42(11):40-51.

[5]LING C B.On the Stresses in a Plate Containing Two Circular Holes[J].Journal of Applied Physics,1948,19(1):77-82.

[6]KOOI C B,VERRUIJT A.Interaction of Circular Holes in an Infinite Elastic Medium[J].Tunnelling and Underground Space Technology,2001,16(1):59-62.

[7]曼莉,阳军生,刘宝琛.浅埋双孔平行隧道开挖围岩应力和位移分析[J].岩土工程学报,2011,33(3):413-419.

MAN Li,YANG Junsheng,LIU Baochen.Stress and Displacement of Surrounding Rock with Shallow Twin-parallel Tunnels[J].Chinese Journal of Geotechnical Engineering,2011,33(3):413-419.

[8]ATTEWELL P B,YEATES J,SELBY A R.Soil Movements Induced by Tunneling and Their Effects on Pipelines and Structures[M].London:Blackie and Son Ltd.,1986.

[9]张晓清,张孟喜,李磊,等.软土盾构隧道近接施工应力迁移规律研究[J].地下空间与工程学报,2014,10(6):1 324-1 329.

ZHANG Xiaoqing,ZHANG Mengxi,LI Lei,et al.Study on Stress Migration Patterns of Approaching Construction for Shield Tunnel in Soft Soil[J].Chinese Journal of Underground Space and Engineering,2014,10(6):1 324-1 329.

[10]张冬梅,宗翔,黄宏伟.盾构隧道掘进引起上方已建隧道的纵向变形研究[J].岩土力学,2014,35(9):2 659-2 666.

ZHANG Dongmei,ZONG Xiang,HUANG Hongwei.Longitudinal Deformation of Existing Tunnel Due To Underlying Shield Tunneling[J].Rock and Soil Mechanics,2014,35(9):2 659-2 666.

[11]孙钧,袁金荣.盾构施工扰动与地层移动及其智能神经网络预测[J].岩土工程学报,2001,23(3):261-267.

SUN Jun,YUAN Jinrong.Soil Disturbance and Ground Movement under Shield Tunneling and Its Intelligent Prediction by Using ANN Technology[J].Chinese Journal of Geotechnical Engineering,2001,23(3):261-267.

[12]CHAPMAN D N,AHN S K,HUNT D V L.Investigating Ground Movements Caused by the Construction of Multiple Tunnels in Soft Ground Using Laboratory Model Tests[J].Canadian Geotechnical Journal,2007,44(6):631-643.

[13]张桓,张子新.盾构隧道开挖引起既有管线的竖向变形[J].同济大学学报,2013,41(8):1 172-1 178.

ZHANG Huan,ZHANG Zixin.Vertical Deflection of Existing Pipeline Due to Shield Tunnelling[J].Journal of Tongji University,2013,41(8):1 172-1 178.

[14]MINDLIN R D.Force at a Point in the Interior of a Semi-infinite Solid[J].Journal of Applied Physics, 1936,7(5):195-202.

[15]LOGANATHAN N,POULOS H G.Analytical Prediction for Tunneling-induced Ground Movements In Clays[J].Journal of Geotechnical and Geoenvironmental Engineering,1998,124(9):846-856.

[16]魏纲,庞思远.双线平行盾构隧道施工引起的三维土体变形研究[J].岩土力学,2014,35(9):2 562-2 568.

WEI Gang,PANG Siyuan.Study of Three-dimensional Soil Deformation Caused by Double-line Parallel Shield Tunnel Construction[J].Rock and Soil Mechanics,2014,35(9):2 562-2 568.

[17]PASTERNAK P L.On a New Method of Analysis of an Elastic Foundation by Means of Two Foundation Constants[D].Moscow:Gosudarstvennoe Izdatelstvo Literaturi po Stroitelstvu I Arkhitecture,1954.

[18]KERR A D.Elastic and Viscoelastic Foundation Models[J].Journal of Applied Mechanics,1964,31(3):491-498.

[19]裴丽.立交隧道近接施工对既有隧道力学特性的影响研究[D].重庆:重庆大学,2010:51-52.

[20]MOLLON G,DIAS D,SOUBRA A.Probabilistic Analyses of Tunneling-induced Ground Movements[J].Acta Geotechnica,2013,8(2):181-199.