基于载荷标定的城际列车转向架载荷及应力分布特征研究
2016-05-08孙守光
邹 骅,李 强,孙守光
(北京交通大学 机械与电子控制工程学院,北京 100044)
车辆构架是列车运行中的关键结构,对其进行安全测试至关重要。目前对构架的测试及评价主要是通过对构架进行载荷与应力的测试,然后进行疲劳损伤的估计。疲劳损伤寿命估计是以数据处理及数据统计方法为基础的,现代设计技术表明,载荷特征掌握越具体,结构寿命预计越准确[1-3]。对大量数据进行合理有效地处理,才能够掌握载荷的真实特征,本文以某城际列车构架载荷标定及线路实测试验为基础,对标定及测试试验的数据进行处理,研究载荷、应力分布特征及相互关系,完成了对线路实测载荷、真实作用载荷、线路实测应力三者分布的估计及相互关系的梳理,形成了城际列车载荷测试研究的系列方法。
1 载荷标定及载荷系关系
对于列车构架载荷的测试,主要的方法是利用有限元分析软件对构架单独施加横向载荷、浮沉载荷、扭转载荷、侧滚载荷、制动载荷、电机载荷等,获得只对各载荷中的某一个载荷响应强烈的点作为载荷识别点[4-6]。然后在各点上组桥路贴应变片,进行载荷标定。分别逐级加载各载荷系,得到载荷识别点对载荷的响应,从而得到识别点的响应结果和实际加载载荷的关系。标定工作在试验室专用疲劳试验台上完成,将工况理想化,假设了各载荷识别点足够理想,且各载荷系完全独立不相互影响,每一个识别点的结果是对所加载载荷的唯一响应。
本文按照上述假设,对某城际列车的构架进行实验室载荷标定试验,逐级加载各系载荷,得到各载荷系识别点及其他测试点对加载载荷的响应。以侧滚载荷加载为例,加载侧滚载荷后各载荷系识别点的响应结果见表1。

表1 各载荷系识别点对侧滚载荷的响应
侧滚载荷的加载及响应结果表明,单系载荷的加载会对所有载荷系识别点造成影响,形成响应。即由于构架结构及测试条件的限制,各载荷系的响应点并不能完全达到假设状态,单一载荷的加载下,各响应均会产生与之对应的唯一响应,因此在多项载荷加载的情况下,各识别点的响应结果是所加所有载荷的叠加,以表1侧滚载荷为例,其关系可表示为
FCC=aCFHJ+bCFFJ+cCFNJ+dCFCJ+
eCFDJ+fCFZJ
(1)
式中:FCC为侧滚载荷系的测试结果;FHJ,FFJ,…,FZJ为加载的横向、浮沉等载荷系的加载数值;aC,bC,…,fC为加载载荷对侧滚载荷识别点的响应系数。
本次测试主要涉及横向载荷FH、浮沉载荷FF、扭转载荷FN、侧滚载荷FC、电机载荷FD、制动载荷FZ,其关系可表示为
(2)
载荷应力测试中,由于部分数据的幅值较小,不对疲劳寿命造成影响[7],因此在数据处理中可以将该部分信号过滤忽略。按照线路测试数据处理经验,可将小于最大响应值5%的数值做归零处理,即将表1中普遍小于侧滚响应5%的响应值设为0,得到部分响应的传递系数为0。为方便处理,将系数进行归一化处理,将所加载荷对最大响应的传递系数设为1。按照以上方法,结合标定结果可得各传递系数为
(3)
式(3)利用标定试验结果将测试响应结果用加载载荷进行表示,将该式应用于线路实测中,其含义为,某一载荷实际测试结果是由各独立的真实载荷系的线性叠加。
载荷标定试验的意义在于寻找加载载荷与实际响应各点的传递关系,所求得的传递关系是基于假设理想的真实载荷,因此利用式(3)反求得到真实载荷,是利用载荷传递系数的基础和前提。同时,载荷标定过程中,加载载荷是理想的真实载荷,为得到与线路实测载荷谱同等效果的实验室载荷谱,需要将测试载荷还原成真实载荷。反解式(3)结果如式(4)所示。
(4)
式(4)利用测试载荷求解出了真实载荷,表明线路实测载荷结果是真实载荷的叠加,直接按照测试载荷进行寿命估算是有重复量的计算,还需要进行一次真实载荷的求解。同时表明本文载荷标定及线路测试中,扭转载荷对横向载荷的影响、侧滚载荷对浮沉载荷及电机载荷的影响均是不可忽略的。
2 真实载荷谱还原
真实载荷是载荷传递及变换的前提,是线路实测载荷转换成实验室试验加载的等效载荷谱的基础。为比较线路实测载荷与真实载荷的区别,将线路实测载荷按照雨流计数法进行编谱处理,得到线路实测各系载荷谱见表2。
同时利用式(4)对线路实测载荷时间历程运算,得到真实载荷的载荷时间历程,按照同样的方法编谱,得到横向载荷、浮沉载荷、电机载荷的真实载荷谱见表3(侧滚、扭转、制动载荷受其他载荷影响较小,本文忽略其影响,可看做真实载荷与线路实测载荷一致,此处不再重复)。

表2 实测数据所得载荷谱
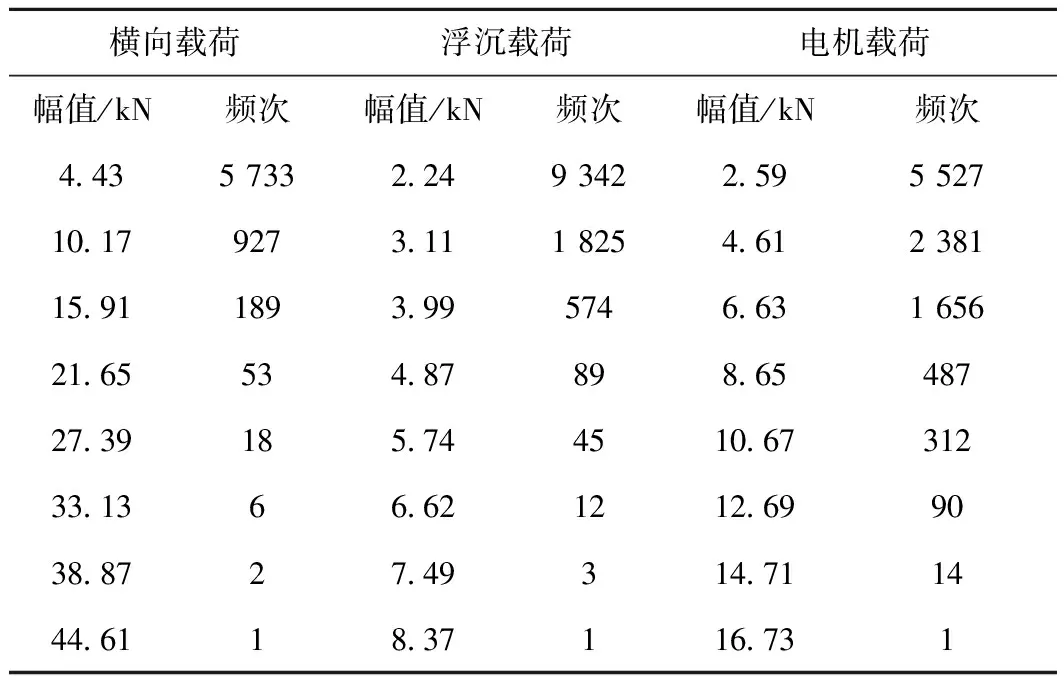
表3 还原后的真实载荷谱
将真实载荷谱与实测载荷比较,还原后的横向真实载荷比实测横向载荷小,还原后的真实浮沉载荷及电机载荷比实测大。进一步证明了线路测试载荷受各系载荷的共同影响,横向载荷、浮沉载荷、电机载荷所受影响较大,不可忽略。
3 载荷谱分布估计
3.1 威布尔分布
为比较载荷的实际区别,对表2、表3中的载荷谱进行分布估计,通常采用的假设理论分布有威布尔分布、对数正态分布[7-9]和截尾正态分布[4],数据处理中发现,威布尔分布对城际列车载荷谱拟合效果最好,对数正态分布次之,截尾正态分布最差。此处利用威布尔分布对载荷谱进行拟合。
三参数威布尔分布其分布函数为
x>γβ>0η≥0
(5)
概率密度函数为
x>γβ>0η>0γ≥0
(6)
式中:β为形状参数;η为尺度参数;γ为位置参数,两参数威布尔分布γ=0。
3.2 卡方检验法分布估计
卡方检验法假设实测应力谱服从某一特定分布,利用分布拟合的卡方检验原理,求解在某分布下数据的最小卡方值,求得卡方值越小时,所对应的参数越接近该特定分布的实际参数[10]。在该基础上,利用计算机程序优化使得载荷谱分布函数的卡方值最小,从而解得分布函数,并同时可对卡方值进行检验。
利用求最小卡方值的方法分别求解实测载荷谱和还原后的真实载荷谱的威布尔分布,其参数估计结果见表4,以横向载荷的真实载荷为例,载荷分布估计如图1所示。

表4 各系载荷谱的分布拟合参数

图1 横向真实载荷的分布拟合
对比表4各参数,同一载荷系的实测载荷和真实载荷,其分布拟合的部分参数接近,表明线路实测载荷谱和真实载荷谱所服从的分布类型接近,这符合具体数据的特性,即各真实载荷系对实测载荷会有影响,但主体载荷分步趋势不会偏差太远。而分布的具体参数又有差异,说明所采用的估计分布函数的卡方检验法对分布变化的灵敏性和合理性。
比较各系载荷分布参数与载荷谱,各位置参数基本都接近载荷谱的最小值(载荷谱的幅值为每一级的中间值,最小值为载荷谱最小中间值减去一半的载荷谱级间距)。
比较实测载荷与真实载荷的分布参数,实测载荷的尺度参数普遍大于真实载荷,说明实测载荷由于载荷的叠加,每个叠加载荷的集中区不一致,故而分布较为分散。实测载荷的形状参数普遍较大,形状参数决定分布的走向和形状,因此实测载荷较真实载荷相比,其分布走向更加陡峭一些。
相互比较各载荷系的参数,电机载荷和浮沉载荷的形状参数较为接近,这与实测过程中,浮沉载荷可能引起构架浮沉从而影响电机载荷的实际情况相一致。
比较实测谱与还原后的真实谱拟合威布尔分布,还原后的谱卡方值更小,更接近于威布尔分布,实测谱是多种理想载荷系的叠加载荷,还原后的载荷系是近似理想的独立载荷,因此,独立载荷更接近服从威布尔分布,所测的载荷是多重载荷的叠加,其拟合的威布尔分布实际是多个威布尔分布的叠加,这也是所测载荷往往并不能精确拟合威布尔分布的原因。
3.3 最值估计与比较
在随机载荷及应力的测试研究中,一般将超越概率10-6所对应的载荷或应力值作为可预测的最大值[11-12]。利用已估计的载荷谱分布可进行载荷谱最大值的估计,反解超越概率下分布函数的概率密度累积函数,得到各估计最值见表5。

表5 各系载荷谱最值估计
比较以上各载荷系分布估计,实测载荷与真实载荷相比,实测载荷的估计最值与实测最值的变化率不够稳定,甚至出现负值,这与最值估计的现实情况不相符,其中横向载荷的变化率43.82%,使得估计最值为71.45 kN,在现实情况中该值偏大。相比而言,真实载荷的最值估计相对合理,变化率为10%~30%。以上结果说明,对真实载荷的还原,影响有两方面,一方面是直接对最大值的影响,即求解后横向载荷减小,浮沉和电机载荷增大。另一方面,是对载荷分布的影响,叠加后的载荷分布受到多载荷系的影响,与独立载荷系分布差别较大。最值估计结果表明,叠加后的载荷系即实测载荷的分布远不及真实载荷的分布有意义。显然,真实载荷对分布的影响大于对最值的影响。
为比较真实载荷最值估计效果,结合本次试验条件进行比对,本次测试车辆及转向架参数见表6。

表6 本次测试车辆及转向架参数
根据UIC615-4标准,转向架构架的垂向载荷Fz和横向载荷Fy为[13]
(7)
Fy=0.5(Fz+0.5m+g)
(8)
式中:nb为转向架数量,本次测试车辆转向架数为2;mv为车辆不同运行级别(如果有必要,应包括燃料和水等负载物)的车辆自重;m+为转向架自重;c2为乘客质量,空车实验此值为0。
求得垂向载荷Fz=70.266 kN,横向载荷Fy=54.145 kN。根据UIC615-4标准建议,构架侧滚载荷系数α=0.1,浮沉载荷系数β=0.2。则侧滚载荷为7.0 kN,浮沉载荷为14.0 kN,横向载荷为54.1 kN。本次估计侧滚载荷最值6.81 kN,浮沉载荷最值10.32 kN,横向载荷最值53.67 kN。
对比实验数据,该线路测试载荷比UIC标准中的设计载荷略小,原因为本次测试是新车上路,工况有所不同。同时浮沉、侧滚载荷谱各级变化较为舒缓,在测试数据量增大的情况下其最值还会增加,此处主要研究载荷及应力最值估计的方法,篇幅限制不再赘述。
3.4 载荷谱外推
线路载荷实测相比列车运行寿命,由于诸多客观条件,只能是一个很有限的样本,其代表性不足。载荷及应力最值估计的重要意义在于载荷谱应力谱的扩展,实测的载荷及应力谱仅能反映实测公里数内的载荷应力状态。利用分布估计及最值估计的结果,反推出更加标准的载荷谱,该谱的特点在于其总频次为106,且包含了测试过程中可能的最大值,同时该谱严格符合某一分布函数。该谱是一种客观的统计结果,能够反映更大公里数范围的载荷及应力的特征,包含了阶段寿命中可能出现的所有载荷值及其出现概率,是最能够代表所测载荷系特性的谱。
利用得到的分布函数,每一级载荷的频次可按式(9)进行推断。
pi=[F(bi)-F(ai)]×hi∈[1,21]
(9)
式中:F(bi)和F(ai)分别为每一区间的上下限所对应的分布函数值,本次测试横向真实载荷的外推谱见表7。
该谱能够为实验室测试提供参考和指导,能够将线路工况更好地转换为实验室可加载的载荷系。
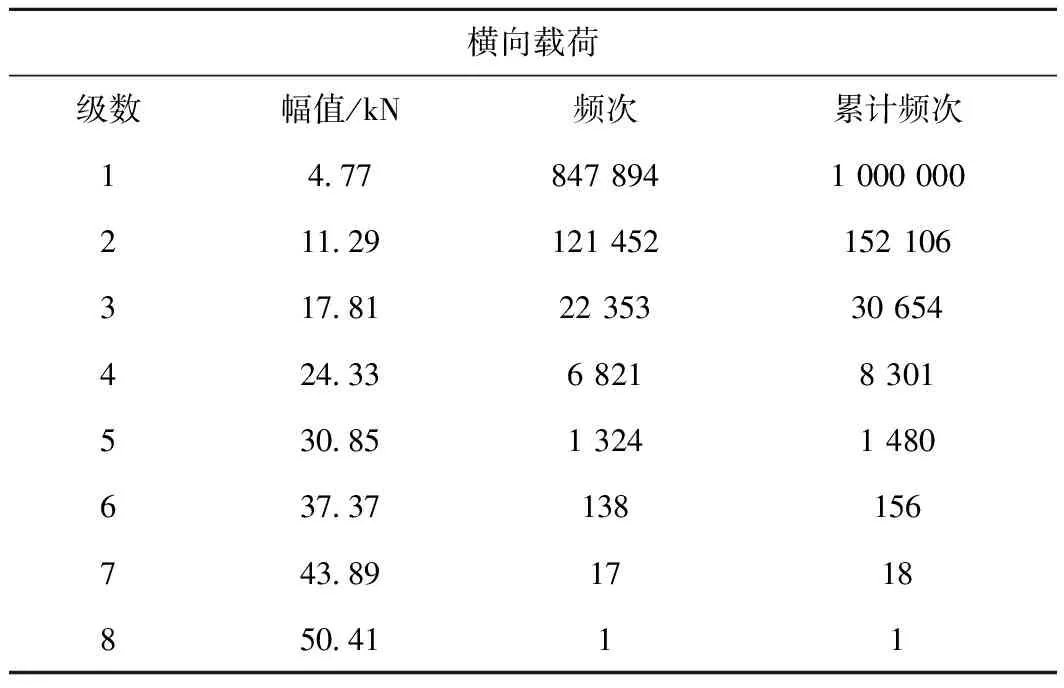
表7 横向真实载荷的推断载荷谱
4 应力谱分布估计
实测载荷为真实载荷的叠加,同理,构架各应力测试点的测试应力也是各个载荷的叠加传递,其叠加过程与载荷相比更加复杂,在数据处理的过程中,利用威布尔分布拟合应力谱分布,其结果并不理想,卡方值往往超出理想范围。
分析其原因,应力是各项载荷的叠加,因此应力的独立性比载荷系差,更容易受其他载荷的影响,所测应力值是诸多载荷重复叠加后的结果,而实际测试中只测试了其叠加结果的某一分量。因此,对于应力的拟合,需比威布尔分布适应性更强的分布。将通常采用的假设理论分布威布尔分布、对数正态分布进行组合,可实现更大适应性地拟合应力分布[12]。按照权重配比组合两个分布,参数φ(1>φ>0)作为权重系数。其组合后的分布概率密度为
f(x)Z=φ·f(x)D+(1-φ)·f(x)W=
x>0β>0η>0
(10)
积分可得累积概率分布函数为
F(x)Z=φ·F(x)D+(1-φ)·F(x)W=
x>0β>0η>0
(11)
选取构架上关键测试点1、2、3、4数据,进行数据处理,并按照上述方法分别进行威布尔分布及组合分布拟合,关键点的选取如图2所示,选取关键点3的组合分布拟合效果如图3所示,分布拟合的卡方值见表8。

图2 关键测试点
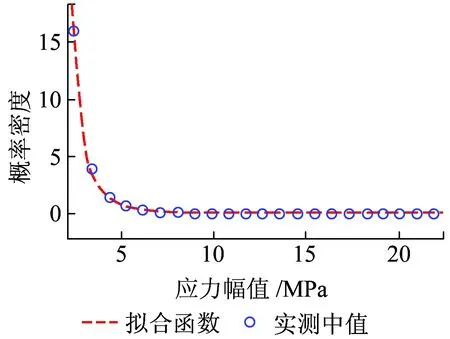
图3 应力谱的组合分布拟合
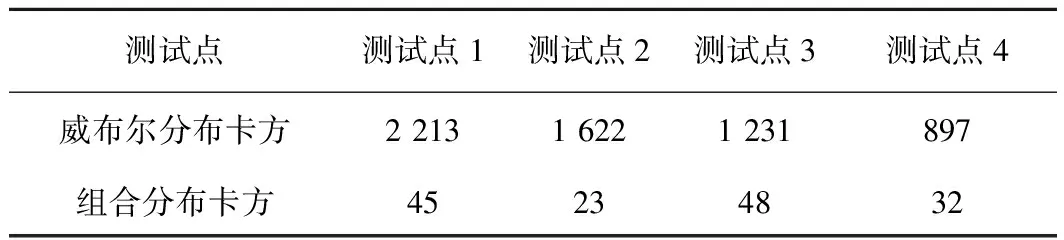
表8 分布拟合卡方值
通过分布估计的卡方值比较,发现威布尔分布和对数正态分布的组合分布对应力谱的适应性远高于某单一分布,也应证了应力是诸多独立载荷的动态叠加结果,其分布的影响因素远多于载荷影响因素,与单一的载荷分布无对应的线性关系。
得到应力分布后,可以进行最值估计及应力谱推断,进而进行损伤计算及寿命估计,篇幅限制不再赘述。
5 结论
本文通过载荷标定及线路实测,引入真实载荷/应力概念,梳理了从载荷标定到线路实测整个过程中的各载荷/应力的关系,估计了各载荷系及关键点应力分布。
(1)由于测试条件及构架结构限制,实测载荷其实质是真实载荷的叠加,求解标定系数方程组还原出独立的真实载荷,真实载荷对分布估计、最值估计、载荷谱推断校准等过程至关重要,是载荷处理的基础。
(2)相比实测载荷谱,还原后的真实载荷谱能够更好地服从威布尔分布。
(3)真实载荷对载荷谱最大值和分布两方面都有重要影响;疲劳寿命估计中,载荷谱分布方面影响更大,因为分布决定了某一载荷出现的频次。
(4)应力是多项载荷系动态传递叠加的结果,威布尔分布难以实现对应力谱分布的拟合,威布尔分布和对数正态分布的组合分布能够良好地实现对应力谱分布的拟合。
(5)真实载荷系虽相互独立,但是依然可以考虑确定载荷系分布参数,对分布参数接近的载荷系进行载荷模型的简化处理。
参考文献:
[1]高镇同.疲劳应用统计学[M].北京:国防工业出版社,1986.
[2]庄楚强,何春雄.应用数理统计基础[M].广州:华南理工大学出版社,2009.
[3]张曙光.高速列车转向架载荷谱测试与建立方法的研究[J].中国科学,2008,38(11):1 805-1 814.
ZHANG Shuguang.Load Test and Spectrum Establish-ment of the High Speed Train[J].China Science,2008,38(11):1 805-1 814.
[4]李强,刘志明,张桂青,等.提速客车转向架动应力分布拟合的研究[J],铁道学报,2001,23(4):105-108.
LI Qiang,LIU Zhiming,ZHANG Guiqing,et al.Research on Distribution of Dynamic Stress for Speed Increased Passenger Car Bogies[J].Journal of the China Railway Society,2001,23(4):105-108.
[5]袁金荣.CRH2-300型动车组转向架构架动载荷识别研究[D].北京:北京交通大学,2008.
[6]刘克格,闫楚良,张书明.飞机主起落架载荷谱实测的台架标定[J].吉林大学学报,2006,36(6):1 025-1 028.
LIU Kege,YAN Chuliang,ZHANG Shuming.Bench Calibration of Load Spectrum Measurement for Fighter Airplane Main Undercarriage[J].Journal of Jilin University, 2006,36(6):1 025-1 028.
[7]凌静,高镇同.多工况机械结构疲劳载荷的统计处理[J].机械强度,1992,4(2):31-34.
LING Jing,GAO Zhentong.The Statistical Treatment for Fatigue Load of a Mechanical Structure under Multioperating Condition[J].Journal of Mechanical Strength,1992,4(2):31-34.
[8]陈爱雅,高镇同.二维随机疲劳载荷的统计处理及其应用[J]. 北京航空学院学报,1986(1):75-85.
CHEN Aiya,GAO Zhentong.The Statistical Processing and Application of Two-dimensional Random Fatigue Load[J].Journal of Beijing Institute of Aviation,1986(1):75-85.
[9]顾明,陈建元.非对称循环载荷二维载荷谱编制的分析及计算程序[J]. 机械强度,1987,9(1):62-68.
GU Ming,CHEN Jianyuan.Asymmetrical Cyclic Load Analysis of the Two-dimension Load Spectrum Compiling and Application[J].Mechanical Strength,1987,9(1):62-68.
[10] 盛骤,谢式千,潘承毅.概率论与数理统计[M].北京:高等教育出版社,2008:199-201.
[11]易当祥,吕国志,周雄伟.用概率推断法确定多工况二维疲劳设计谱的载荷最大值[J]. 应用力学学报,2006,23(3):484-487.
YI Dangxiang,LÜ Guozhi,ZHOU Xiongwei.Maximal Loading Calculation for Two Dimensional Fatigue Design Spectrum under Multiple Working Conditions with Probability Extrapolation Method[J]. Chinese Journal of Applied Mechanics,2006,23(3):484-487.
[12]薛广进,李强.轨道车辆结构动应力谱分布的估计[J].机械工程学报,2013,49(4):102-106.
XUE Guangjin,LI Qiang.Estimation of Distribution for Rail Vehicle Dynamic Stress[J].Journal of Mechanical Engineering,2013,49(4):102-106.
[13]刘德刚,刘宏友,李庆升.转向架构架强度试验标准对比[J].铁道车辆,2011,49(9):12-17.
LIU Degang,LIU Hongyou,LI Qingsheng.Comparison of Strength Test Standards[J].Rolling Stock,2011,49(9):12-17.
