基于RBPF的轨道车辆悬挂系统参数估计方法

方 宇，李晓斌，金子博，高 伟

(上海工程技术大学 城市轨道交通学院，上海 201620)

悬挂系统的状态直接影响轨道车辆运行的安全性、平稳性和舒适性。据统计，在轨道车辆产生的众多故障中，转向架悬挂系统故障频率最高，占总数的1/3左右[1]，是车辆故障中比例最大的一部分。目前悬挂系统在线监测主要依赖于信号分析方法，需在轨道车辆上布置数目较多的传感器，主要遵循研究关键部件检测信号特性的突变，包括幅值、频率特性以及对动力学参数的统计特征进行分析，检测结果可靠性较低，具有一定的局限性[2]。

参数估计是近年来提出的一种全新的车辆状态监测方法，在实际应用时只需利用少量的传感器获取车辆振动状态信息，就能够估算出车辆关键部件实际参数值，因此相对信号分析方法具备一定的优势。文献[3，4]提出了一种基于卡尔曼滤波和粒子滤波的参数估计算法，利用该算法估计了轨道车辆正常状态下二系横向减震器阻尼、抗蛇行减震器阻尼及轮对等效锥度的参数值，获得较为理想的效果，但是没有深入研究车辆故障状态下这些部件的参数估计算法。文献[5]提出一种新型的轨道车辆悬挂系统状态监测方法，引入了再次均匀采样策略，有效克服了传统参数估计算法因粒子枯竭而无法对悬挂系统故障进行监测的缺陷，但是算法中所需的观测值是通过车辆系统仿真模拟得到，没有深入研究从轨道车辆SIMPACK整车模型或实车试验中获得观测信息。

本文主要研究RBPF参数估计方法，利用多体动力学仿真和实车试验获取振动数据，结合RBPF算法估计轨道车辆在不同工况下的二系横向减震器实际参数值，估计结果验证了参数估计方法的有效性和准确性。

1 轨道车辆SIMPACK整车模型的建立

以国内某典型轨道车辆为研究对象，车辆部分参数见表1，利用SIMPACK软件建立轨道车辆整车模型。在多体系统中，拓扑结构建立是系统建模的一个十分关键的前期工作，多体系统拓扑图建立的好坏直接和模型建立的正确与否密切相关。拓扑关系主要由车体、构架和轮对三大部件组成[6]，通过约束形式、铰接形式以及力元形式来表示不同刚体之间的连接关系，轨道车辆系统拓扑图如图1所示。

表1 车辆参数

利用SIMPACK软件建立的轨道车辆整车模型如图2所示，文中主要利用建立的整车模型获得车体、构架、轮对的振动加速度、角加速度等后处理信息，作为RBPF算法中的实际观测值，对轨道车辆悬挂系统关键部件参数进行估计。

图1 轨道车辆系统拓扑图

图2 轨道车辆整车模型

2 轨道车辆系统横向动力学半车模型和状态空间模型建立

轨道车辆后半车模型平面图如图3所示，对应于图2中轮对1、轮对2、后转向架构架及半个车体，由于只建立半车模型，因此车体只考虑1个横向运动的自由度，而轮对和构架均有横向和摇头运动2个自由度。图中：yw1和yw2分别为轮对1、轮对2的横移量；ψw1和ψw2分别为轮对1、轮对2的摇头角；yb和ybd分别为构架和车体的横向位移；ψb为构架的摇头角。同理，也可建立由轮对3、轮对4、前转向架构架及半个车体构成的前半车模型。

图3 轨道车辆后半车模型平面图

轨道车辆系统横向动力学半车模型振动方程为

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

式中：yt1和yt2分别为作用在2个轮对上的轨道横向不平顺；yd1和yd2分别为2个轮对在轮轨接触点处的横向位移；Iw1和Iw2分别为2个轮对的转动惯量；Ib为构架的转动惯量；f11和f22分别为纵向和横向蠕滑系数；λ为轮对等效锥度；v为车辆运行速度。将系统横向动力学模型变换为状态空间模型如下

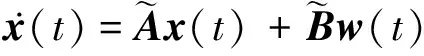
(11)

y(t)=Hx(t)+v(t)

(12)

式(11)为时间t的连续函数，将其离散化[7]并结合式(12)可得到离散化后的系统横向动态空间模型为

xk+1=A(θ)xk+B(θ)wk

(13)

yk+1=H(θ)xk+1+vk+1

(14)

式中：w和v分别为相互独立的状态噪声和观测噪声向量；A(θ)，B(θ)和H(θ)是由θ决定的矩阵。

3 RBPF算法在轨道车辆悬挂系统参数估计中的应用

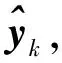
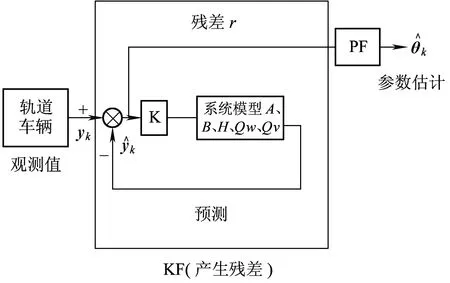
图4 RBPF参数估计算法流程图

此时，系统动态空间模型可以表示为

xk=A(θ)xk-1+B(θ)wk-1

(15)

yk=H(θ)xk+vk

(16)

参数估计过程中状态噪声w为轨道横向不平顺，方差阵Q[9]为

式中：Ar为轨道粗糙度因素，取Ar=2×0.33×10-3；Ts为采样时间间隔，取Ts=0.001 s。

观测噪声协方差矩阵设为均值为零的定长平稳随机白噪声序列，方差阵R为[10]

R=0.001|max(yk(n))-min(yk(n))|

n=1，2，3，4，5，6，7

式中：max(yk(n))和min(yk(n))分别是第n个观测量在整个时间历程中的最大值和最小值。

假设初始状态估计值为x0，初始的状态估计方差P0是17阶稀疏矩阵，一般方差P0设置较小，这样可避免因对滤波值造成过大的扰动而导致失真。未知参数向量θ的变化范围为[θmin，θmax]，粒子数量为M。RBPF算法步骤如下：

步骤1初始化。在区间[θmin，θmax]内均匀采样，组成粒子集θ1|0(i)，初始状态x1|0(i)=x0，初始状态方差P1|0(i)=P0，i=1，2，3，…，M。

步骤2在每个时刻k(k=1，2，…)，重复以下步骤：

yk|k-1(i)=H(θk|k-1(i))xk|k-1(i)

(17)

Rk(i)=H(θk|k-1(i))Pk|k-1(i)HΤ(θk|k-1(i))+R

(18)

(19)

(20)

式中：各时刻观测向量yk可从SIMPACK整车模型和实车试验中获得，各个粒子的权值服从多维正态分布函数。

(21)

(3)重采样。首先产生M个在[0，1]区间均匀分布的随机数up(p=1，2，…，M)，通过搜索算法找到满足以下条件的整数l。

(22)

l=1，2，3，…，M

记录第l个粒子，即对该粒子进行了M重复采样，同时保留相应的θk(i)，xk|k-1(l)，Pk|k-1(l)，得到新的参数、状态和方差组合。

(4)卡尔曼滤波测量更新。获得k时刻卡尔曼滤波增益Kk(i)、状态估计值xk(i)估计均方误差Pk(i)分别为

Rk(i)=H(θk(i))Pk|k-1(i)HT(θk(i))+R

(23)

(24)

xk(i)=xk|k-1(i)+Kk(i)(yk-H(θk(i))xk|k-1(i))

(25)

Pk(i)=Pk|k-1(i)-Kk(i)H(θk(i))Pk|k-1(i)

(26)

(5)粒子滤波时间预测更新。

(27)

(6)卡尔曼滤波测量更新，得到k+1时刻估计的状态xk+1|k(i)和估计方差Pk+1|k(i)一步预测更新。

xk+1|k(i)=A(θk+1|k(i))xk(i)

(28)

Pk+1|k(i)=A(θk+1|k(i))Pk(i)AT(θk+1|k(i))+

B(θk+1|k(i))QBT(θk+1|k(i))

(29)

4 正常情况下算法验证

4.1 试验目的及条件

选取既定的轨道车辆进行试验，目前该车转向架二系横向减震器处于工作正常状态，利用真实的振动测试数据作为RBPF参数估计算法中观测值，估计前、后转向架二系横向减震器实际阻尼值，从而验证车辆关键部件正常情况下参数估计算法的正确性。

4.1.1 试验平台和系统组成

整个车载系统主要由数据采集器、工业交换机、车载服务器和GPS(测速模块)构成，车载服务器通过车内局域网对整个采集系统进行控制。车载服务器系统采集各部件的振动状态信息。速度信息由GPS提供，并获取当前车辆运行工况。在整个试验过程中，车辆检测系统通过存储卡将原始信号数据全部本地存储，待停止试验后取出振动数据。

4.1.2 车辆参数和传感器布置

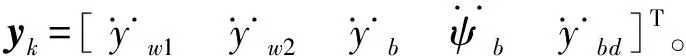
图5 车体加速度计安装实物图

图6 构架加速度计安装实物图

图7 轴箱加速度计安装实物图

图8 构架陀螺仪安装实物图

4.2 试验结果分析

文中主要以后半车模型悬挂系统为例，估计二系横向减震器阻尼值。整个计算过程中，选取一段时间的数据，其速度-时间关系曲线如图9所示。

图9 速度-时间关系曲线

对现场数据采集器采集的实际振动测试数据，采用巴特沃斯低通滤波器进行预处理，利用MATLAB软件编写程序来验证正常情况下RBPF算法的正确性，选取粒子数量M=200，图10分别给出了车速为v=5 km/h、v=10 km/h、v=15 km/h、v=20 km/h四种不同工况下的参数估计结果。

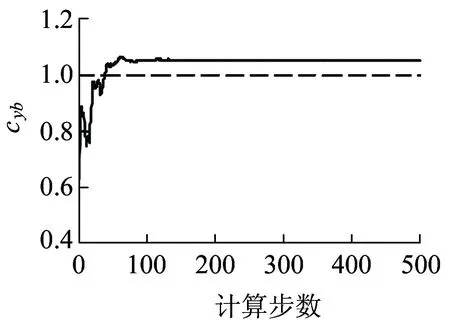
(a)v=5 km/h

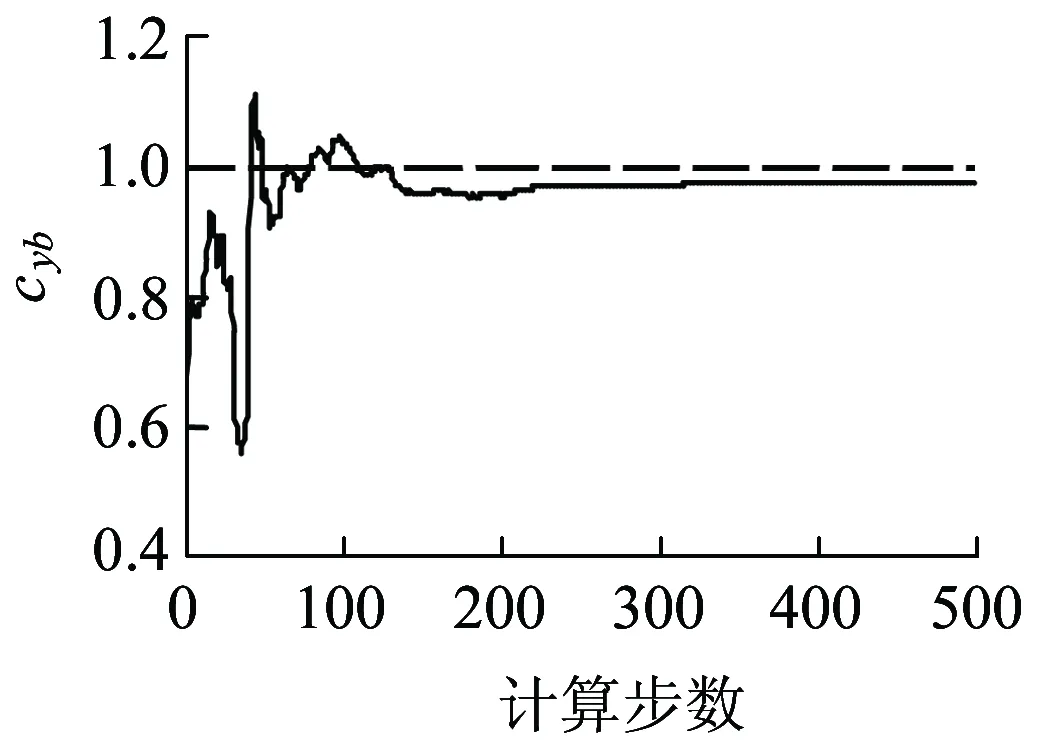
(b)v=10 km/h

(c)v=15 km/h

(d)v=20 km/h图10 不同速度下cyb估计结果

图10中，二系横向减震器cyb估计值已进行归一化处理，即图中纵坐标数值为“1”代表二系横向减震器部件正常(cyb=29 500 N·s·m-1)；纵坐标数值为“0.5”代表二系横向减震器阻尼参数值缩小1倍(cyb=14 750 N·s·m-1)；纵坐标数值为“0”代表二系横向减震器已完全失效，以此类推。由图10可知：实车试验获得的观测值虽然少了轮对摇头角加速度，估计值仍能够很快的收敛到正常值(这里指cyb无故障时实际参数值)附近，并且车速快慢对参数估计结果影响不大。虽然在整个试验过程中可能会因为传感器的测量误差及安装位置会造成估计值与正常值有一定的偏差，但参数估计值整体趋势基本与正常值相吻合，参数估计结果与实际情况相符，验证了正常情况下参数估计算法的正确性，用同样的方法估计得到前转向架二系横向减震器目前同样处于正常状态，估计结果与实际情况也相符。

5 模拟故障情况下算法验证

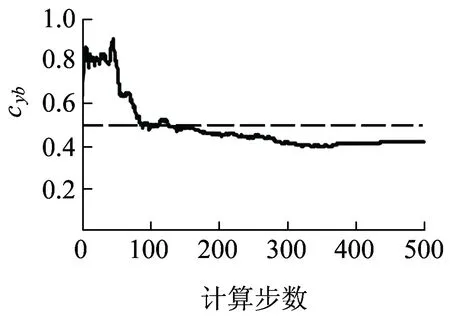
(a)前转向架cyb缩小至0.5

(b)后转向架cyb正常

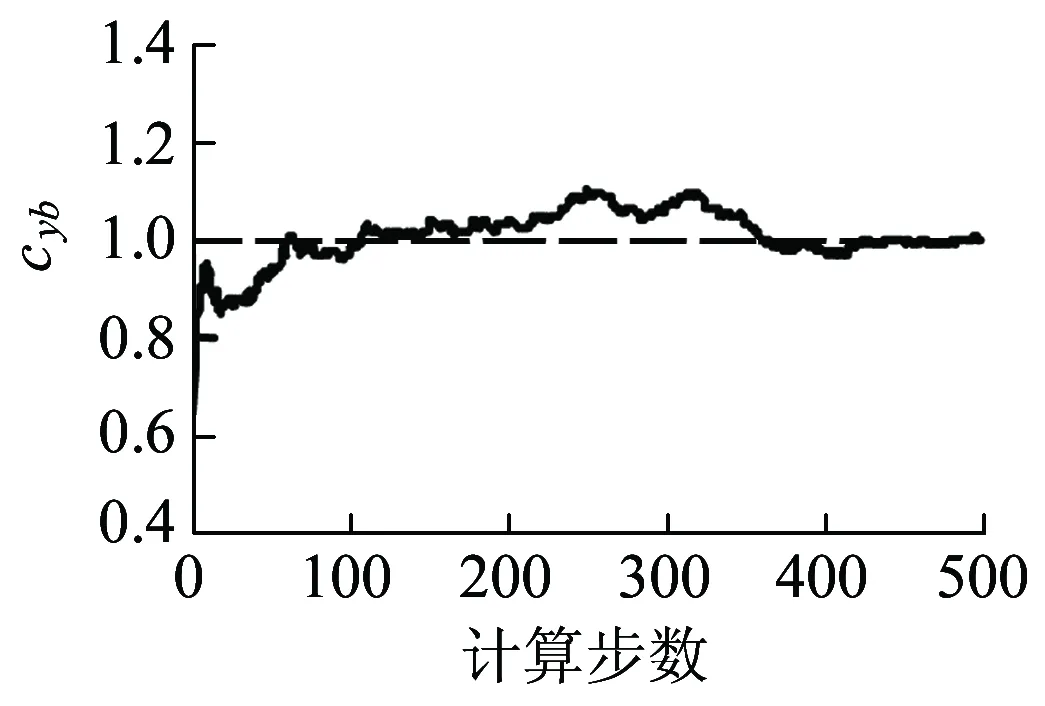
(c)前转向架cyb正常

(d)后转向架cyb缩小至0.5

(e)前转向架cyb缩小至0.7

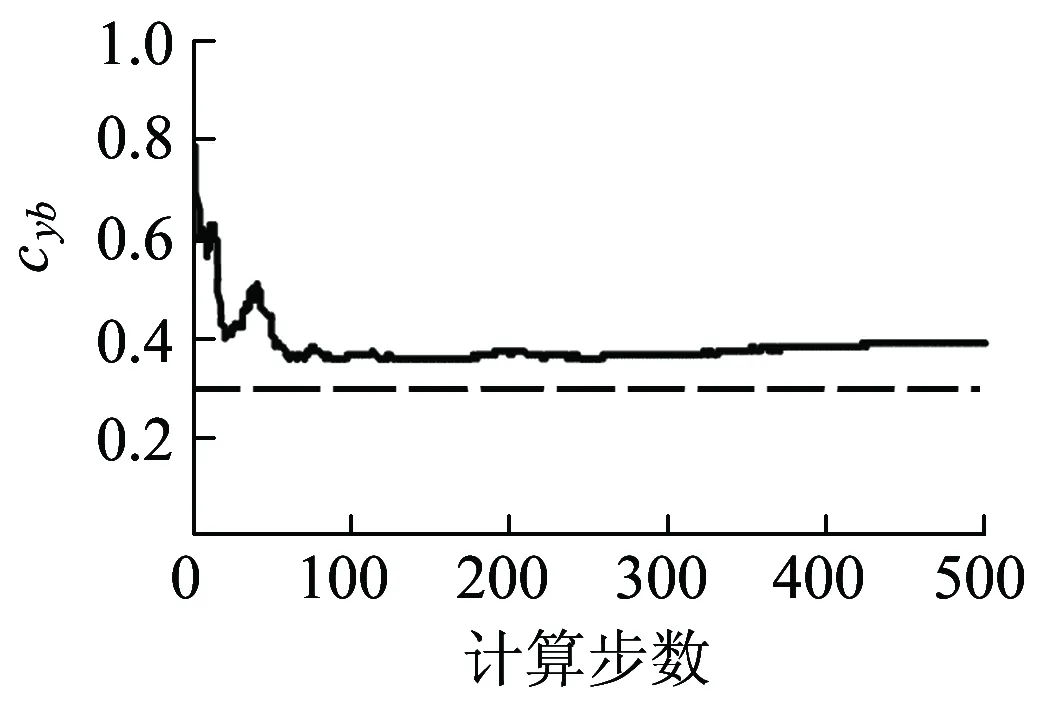
(f)后转向架cyb缩小至0.3

(h)前转向架cyb正常

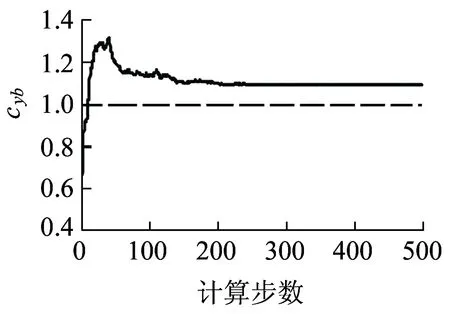
(g)后转向架cyb正常图11 前后转向架参数估计结果

图11是轨道车辆前、后转向架二系横向减震器不同故障下进行的参数估计，分为前转向架cyb故障，后转向架cyb正常；前转向架cyb正常，后转向架cyb故障；前、后转向架cyb均故障；前、后转向架cyb均正常四种工况。以前、后转向架cyb均故障为例，图11(e)表示前转向架cyb阻尼值缩小至正常值0.7倍左右，而图11(f)表示后转向架cyb阻尼值缩小至正常值0.3倍左右，相比得到后转向架二系横向减震器故障程度比前转向架更严重。从图11可以看出，利用SIMPACK整车模型输出的观测向量yk，结合RBPF参数估计算法都能够有效对二系横向减震器cyb故障情况下实际参数值进行估计。计算步数达到约500时估计值就能收敛到真实值附近，并且估计值非常接近参数的真实值，故障情况下算法的正确性得到验证，监测实时性也得到保障。

6 结束语

本文建立了国内某型轨道车辆横向动力学半车模型和状态空间模型，引入RBPF算法，结合多体动力学仿真和实车试验的振动数据，对轨道车辆悬挂系统关键部件之一的二系横向减震器参数进行估计，结果表明：该方法能准确有效地估计得到悬挂系统关键部件正常或故障工况下实际参数值，为车辆关键部件在线状态监测和安全预警提供了重要的理论依据。

参考文献：

[1]陈龙.基于粒子滤波的城轨车辆状态监测方法研究[D].上海:上海工程技术大学,2013:56-58.

[2]漆瑾.高速机车走行部实时在线监测与诊断方法的研究[D].成都：西南交通大学,2006:4-6.

[3] LI P,GOODALL R, WESTON P.Estimation of Railway Vehicle Suspension Parameters for Condition Monitoring[J].Control Engineering Practice,2007,15(1):43-55.

[4]LI P,GOODALL R, KADIRKAMANATHAN V. Estimation of Parameters in a Linear State Space Model Using a Rao Blackwellised Particle Filter[J].Control Theory Application,2004,151(6):727-738.

[5]方宇，陈龙，李晓斌，等.基于再次均匀采样策略改进轨道车辆二系悬挂系统参数估计方法[J].中国铁道科学,2013,34(3)：72-78.

FANG Yu,CHEN Long,LI Xiaobin,et al.Estimation Method for the Secondary Suspension System Parameters of Railway Vehicle Improved by Repeated Uniform Sampling Strategy[J].China Railway Science,2013,34(3):72-78.

[6]缪炳荣，罗仁，王哲，等.SIMPACK动力学分析高级教程[M].成都：西南交通大学出版社，2010.

[7]方宇，陈龙，郑树彬，等.基于参数估计的轨道车辆悬挂系统状态监测方法[J].铁道学报，2013，35(5)：15-20.

FANG Yu,CHEN Long,ZHENG Shubin,et al.Condition Monitoring of Rail Vehicle Suspension System Based on Parameter Estimation[J].Journal of the China Railway Society,2013,35(5):15-20.

[8]DOUCET A,GODSILL S,ANDRIEU C.On Sequential Monte Carlo Sampling Methods for Bayesian Filtering[J].Statistics and Computing,2000,10(3):197-208.

[9]LI H.Measuring Systems for Active Steering of Railway Vehicles[D]. Loughborough: Loughborough University, 2001.

[10]林棻，赵又群，徐朔南.基于粒子滤波算法的汽车状态估计技术[J].农业机械学报,2011,42(2)：23-27.

LIN Fen,ZHAO Youqun,XU Shuonan.Vehicle States Estimation Technology Based on Particle Filter Algorithm[J].Transactions of the Chinese Society for Agricultural Machinery,2011,42(2)：23-27.

[11]丁建明.车辆动力学性能参数估计方法研究[D].成都:西南交通大学，2011:38-39.

[12]刘春生，胡寿松.一类基于状态估计的非线性系统的智能故障诊断[J].控制与决策,2005,20(5):557-561.

LIU Chunsheng,HU Shousong.Intelligent Nonlinear Fault Diagnosis Based on State Estimator[J].Control and Decision,2005,20(5):557-561.