碳酸盐岩地层电成像测井孔隙度谱截止值计算方法

史飞洲, 王彦春, 陈剑光

(1.中国地质大学(北京)地球物理与信息技术学院, 北京 100083;2.中石化地球物理公司云南分公司, 云南 昆明 650233)

0 引 言

碳酸盐岩地层中,常规测井资料计算的孔隙度常与试油结论不符,即孔隙度高的储层产量低,而孔隙度低的储层产量高。这是因为碳酸盐岩地层具有由基质孔隙和次生孔隙组成的双孔隙结构。因此,将基质孔隙与次生孔隙区分开,有利于储层有效孔隙度计算和储层有效性评价。但是,利用常规测井资料很难区分基质孔隙与次生孔隙。斯伦贝谢公司的Newberry等[1]将电成像测井资料转换为孔隙度谱,计算孔隙度谱的截止值,并计算次生孔隙度;Ramakrishnan等[2]也提出了计算孔隙度谱截止值的方法。中国对电成像测井孔隙度谱的研究以定性研究为主,有关孔隙度谱截止值计算方法的研究还比较少[3-9]。

本文利用高斯函数拟合法计算了电成像测井孔隙度谱的截止值,并将其同Newberry和Ramakrishnan的方法进行了对比,在此基础上,将3种方法应用到实际井中,尝试着分析了次生孔隙度大小与储层产能之间的关系。

1 电成像测井孔隙度谱的基本原理

孔隙度谱是孔隙度值的频率直方图。如图1所示,电成像测井仪所测量的是井壁的视电导率值,通过转换就能够获得井壁的视电阻率值,利用阿尔奇公式将井壁的视电阻率矩阵转换为井壁的孔隙度矩阵,对某一深度范围内的孔隙度值在不同的孔隙度值区间内进行数量统计,将统计的结果在坐标系内绘制成频率直方图,就得到了所谓的孔隙度谱。

2 电成像测井孔隙度谱截止值

研究区碳酸盐岩地层具有基质孔隙和次生孔隙组成的双孔隙结构,且次生孔隙以裂缝和孔洞为主,由于基质孔隙与次生孔隙的大小存在一定的差异,因此在孔隙度谱上出现了典型的双峰响应特征,一般认为孔隙度谱的前部(孔隙度较小处)是基质孔隙,孔隙度谱的后部(孔隙度较大处)是次生孔隙。孔隙度谱的截止值即基质孔隙与次生孔隙的分界点(见图1)。

3 电成像测井孔隙度谱截止值计算方法

3.1 高斯函数拟合法

高斯函数拟合法是利用高斯函数对孔隙度谱的双峰进行拟合,然后对拟合后的高斯函数在孔隙度区间内求取函数的交点,该交点就是孔隙度谱的截止值。高斯函数

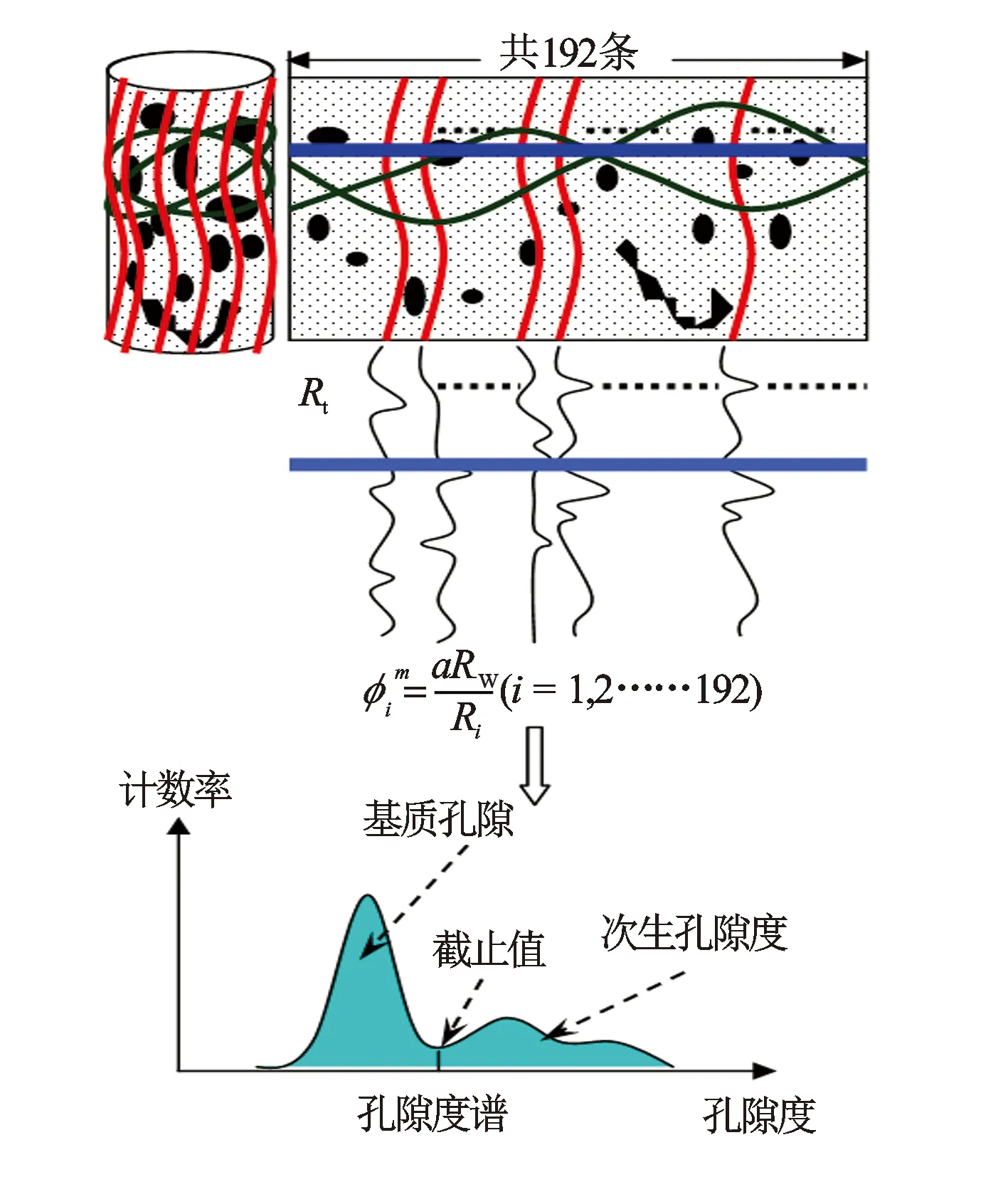
图1 电成像测井孔隙度谱原理图[10]

(1)

对函数两边取自然对数,得

(2)

y=cx2+bx+a

(3)

运用最小二乘法计算a、b、c的值,如式(4)所示。将a、b、c带入式(3),得到拟合公式。

用该方法对实验数据求取了截止值。如图2所示,蓝色实线为用实验数据绘制的孔隙度谱,红色实线为孔隙度谱前部的拟合曲线,粉色实线为孔隙度谱后部的拟合曲线,红色实线和粉色实线的交点横坐标为5,即求取的截止值T=5。

图2 高斯函数拟合法计算的截止值

(4)

3.2 Newberry方法

Newberry等[1]提出了Newberry方法,其思路:①计算最小孔隙度与最大孔隙度之间的孔隙度中值(即最小孔隙度与最大孔隙度之和除以2);②计算最小孔隙度与孔隙度中值区间的孔隙度计数率的和并求取该区间内每个孔隙度的计数率占总计数率的百分比(即每点的概率);③计算最小孔隙度与孔隙度中值区间的孔隙度期望;④计算最小孔隙度与孔隙度中值区间的孔隙度方差,用该方差乘以一个固定的系数(一般取3,但是也可以根据实际情况进行调整),得到孔隙度谱的截止值。用该方法对图2中的实验数据计算了截止值,T≈5.6。

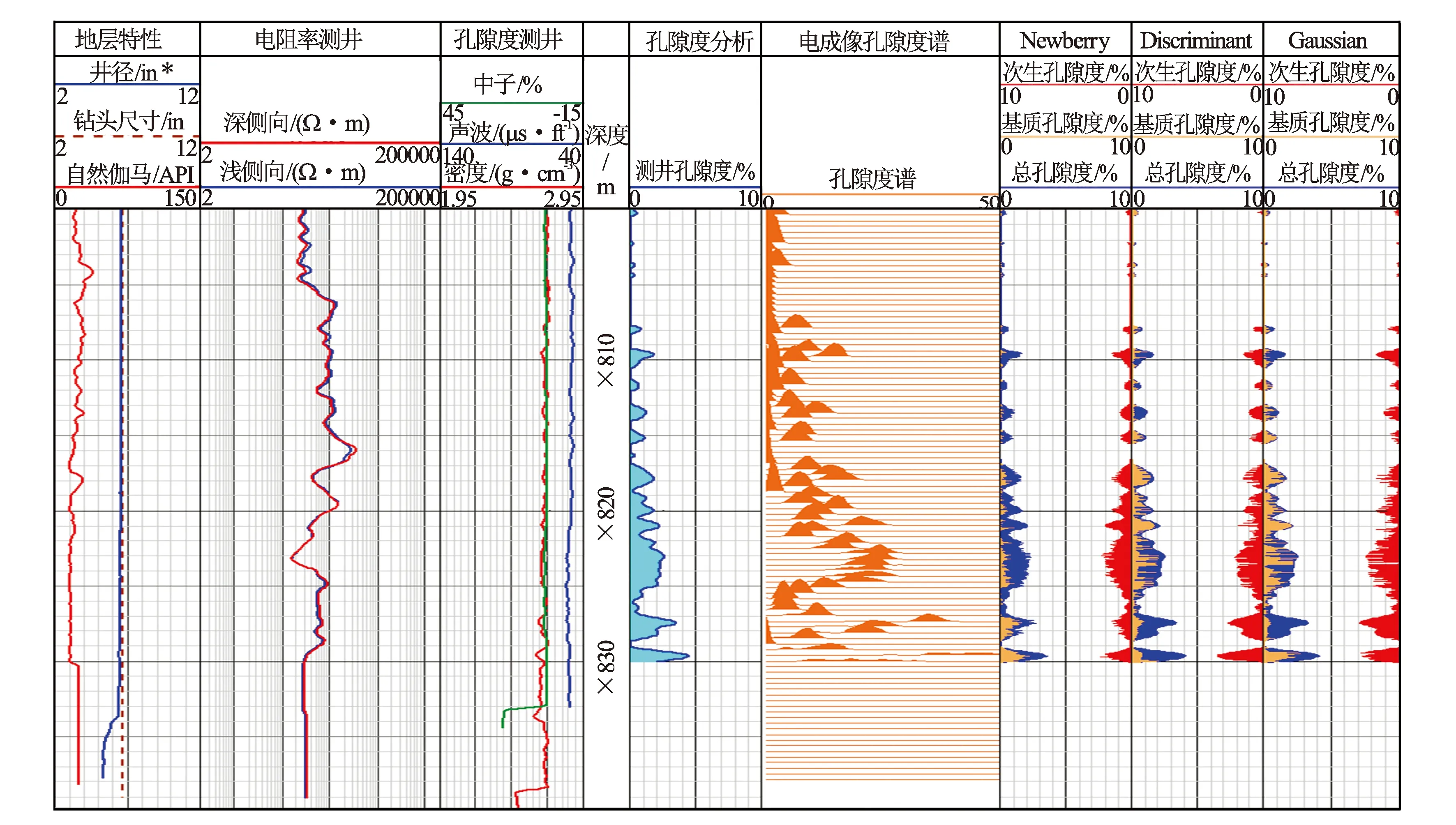
图3 A井电成像测井孔隙度谱分析成果图*非法定计量单位,1 ft=12 in=0.304 8 m,下同

3.3 判别式截止值选择法

斯伦贝谢公司道尔研究中心的Ramakrishnan等[2]提出了这种截止值的计算方法,被称为判别式截止值选择法。该方法是基于模式识别以及统计学领域的标准线性判别式分析方法。该方法的基本思路:计算每个孔隙度值处的判别式的值,求取最大的判别式值,认为最大判别式值处的孔隙度值就是截止值的位置。该判别式为

(1≤k≤N)

(5)

最佳截止值的位置用式(6)求取

G(k*)=maxG(k) (1≤k≤N)

(6)

用该方法对图2中的实验数据计算了截止值,T=6。

4 实例分析

研究区碳酸盐岩地层中,次生孔隙主要包括溶孔和裂缝,其孔隙度相对于基质孔隙要高,孔隙间的连通性较好,有利于储层流体的储集和运移。因此,如果储层含有油气的话,次生孔隙组分高的储层对油气产量的贡献应该大于次生孔隙组分低的储层对油气产量的贡献。

图4 B井电成像测井孔隙度谱分析成果图

分别用Newberry方法、判别式截止值选择法和高斯函数拟合法对A井和B井的电成像测井孔隙度谱计算了截止值,并利用截止值计算了基质孔隙度和次生孔隙度。图3和图4分别为A井和B井的电成像测井孔隙度谱分析成果图。图3和图4中第7、8、9道分别为用Newberry方法、判别式截止值选择法和高斯函数拟合法求取的孔隙度谱截止值计算的基质孔隙度和次生孔隙度,图3和图4中灰色充填部分为基质孔隙度,蓝色充填部分为次生孔隙度,将蓝色充填单独挖出来放到右侧并用红色充填。图5和图6分别为A井和B井的静态电成像测井图像。

图5 A井电成像测井图像 图6 B井电成像测井图像

对比图3和图4,A井和B井的总孔隙度均在2%左右,而A井的次生孔隙度明显高于B井的次生孔隙度,说明A井的储层有效性要好于B井。对A井的井段×685～×825 m进行了试油,用4 mm油嘴求产,日产油142.99 m3,测试结论:油层。对B井的井段×974～×980 m进行了试油,用4 mm油嘴求产,折日产油92 m3,测试结论:差油层。从试油结果可以看到,A井的产量较高于B井的产量,而A井的次生孔隙度也高于B井的次生孔隙度,2井产量之间的差异与2井次生孔隙度之间的差异存在着较好的匹配关系。

3种方法在稳定性和准确性上存在较大的差异。稳定性方面,Newberry方法和判别式截止值选择法要强于高斯函数拟合法。高斯函数拟合法主要是基于孔隙度谱的形状,对于大多数的双峰该方法是适用的,但是也存在特殊情况,如果孔隙度谱双峰的距离过大,在求取高斯拟合函数的过程中就可能出现c值为正数的情况,这时程序会提示错误而终止;而Newberry方法和判别式截止值选择方法均是基于孔隙度值的数学运算,与孔隙度谱的形状没有太大的关系,对任何形状的孔隙度谱均能计算出截止值。准确性方面,高斯函数拟合法的准确性要强于Newberry方法和判别式截止值选择法。A井×820～×825 m井段的孔隙度谱相对于其他深度段的孔隙度谱整体呈现出靠后以及双峰的特征,且孔隙度谱的后部要明显高于前部,说明该深度段的孔隙性较好且次生孔隙也比较发育,高斯函数拟合法所计算的次生孔隙度与孔隙度谱匹配较好(见图3)。B井×972～×990 m井段的孔隙度谱整体呈现出靠前以及单峰的特征,说明该深度段的孔隙性较差,并且以基质孔隙为主,高斯函数拟合法计算的次生孔隙度与孔隙度谱匹配较好(见图4)。

5 结 论

(1) 在碳酸盐岩地层中,次生孔隙组分高的储层对油气产量的贡献大于次生孔隙组分低的储层对油气产量的贡献。

(2) 3种计算孔隙度谱截止值的方法在稳定性和准确性上存在较大的差异。稳定性方面,Newberry方法和判别式截止值选择法的稳定性要好于高斯函数拟合法。准确性方面,高斯函数拟合法的准确性要高于Newberry方法和判别式截止值选择法。

参考文献:

[1] Newberry B M, Grace L M, Stief D D. Analysis of Carbonate Dual Porosity Systems from Borehole Electrical Images [C]∥Permian Basin Oil & Gas Recovery Conference. Midland, Texas: Richardson, 1996: 123-129.

[2] Ramakrishnan T S, Ramamoorthy R, Fordham E, et al. A Model-based Interpretation Methodology for Evaluating Carbonate Reservoirs [C]∥SPE Annual Technical Conference and Exhibition. New Orleans, Louisiana: Richardson, 1997: 1-15.

[3] 曹毅民, 章成广, 杨维英, 等. 裂缝性储层电成像测井孔隙度定量评价方法研究 [J]. 测井技术, 2006, 30(3): 237-239.

[4] 孟凡顺, 冯庆付, 杨祥瑞. 利用电成像测井资料分析次生孔隙率 [J]. 石油地球物理勘探, 2006, 41(2): 221-225.

[5] 李晓辉, 周彦球, 缑艳红, 等. 电成像测井孔隙度分析技术及其在碳酸盐岩储层产能预测中的应用 [J]. 吉林大学学报: 地球科学版, 2012, 42(4): 928-934.

[6] 朱小露, 贺洪举, 刘瑞林, 等. 川中地区震旦系灯影组白云岩储层成像孔隙度分布谱响应特征研究 [J]. 石油天然气学报: 江汉石油学院学报, 2013, 35(4): 83-88.

[7] 周彦球, 李晓辉, 范晓敏. 成像测井孔隙度频谱技术与岩心孔隙分析资料对比研究 [J]. 测井技术, 2014, 38(3): 309-314.

[8] 刘丹, 潘保芝, 房春慧, 等. 利用成像测井评价储层孔隙空间的二维非均质性 [J]. 世界地质, 2014, 33(3): 640-646.

[9] 王宏建, 李庆峰, 赵杰, 等. 塔东古城地区碳酸盐岩储层测井评价 [J]. 大庆石油地质与开发, 2014, 33(5): 215-219.

[10] 吴兴能, 刘瑞林, 雷军, 等. 电成像测井资料变换为孔隙度分布图像的研究 [J]. 测井技术, 2008, 32(1): 53-56.