基于SAPSO优化灰色神经网络的空中目标威胁估计

刘海波, 王和平,2, 沈立顶

(1.西北工业大学 航空学院, 陕西 西安　710072; 2.西北工业大学 深圳研究院, 广东 深圳　518057)



基于SAPSO优化灰色神经网络的空中目标威胁估计

刘海波1, 王和平1,2, 沈立顶1

(1.西北工业大学 航空学院, 陕西 西安710072; 2.西北工业大学 深圳研究院, 广东 深圳518057)

摘要：针对目标威胁估计有很多不确定性的特点，分析了传统目标威胁估计方法和灰色神经网络初始参数随机选择的不足。采用模拟退火改进的粒子群算法代替梯度修正法，对网络参数初始值进行寻优，并通过该方法搜寻到的最优粒子，建立了基于模拟退火粒子群算法优化的灰色神经网络模型，以提高预测模型的稳健性和精确度。与灰色神经网络和没有改进的粒子群灰色神经网络等方法进行比较，仿真实验结果表明，模拟退火粒子群优化的灰色神经网络具有很好的预测能力，可以准确地完成空中目标威胁估计。

关键词：灰色系统；神经网络；模拟退火；粒子群算法；目标威胁估计

随着航空科学技术的高速发展，空中来袭目标类型多样，运动特征多变，多目标拦截能力已经成为防空武器系统的研究方向和衡量防空作战能力的一个重要指标，根据空防态势对敌方目标威胁性做出合理评估是多目标攻击的关键技术之一，它是目标和火力分配的前提。目前常用的目标威胁估计方法有直觉模糊集[1-4]、贝叶斯推理[5-6]、多属性决策法[7]、优劣解距离法[8]、折衷排序法[9]等。上述方法在确定威胁指标权重时，一定程度上依据专家经验，对各因素权值的处理主观性强，不能随作战环境的变化迅速变化，很难准确映射出威胁因素间的复杂关系。近年来以神经网络为代表的智能技术在预测领域得到了广泛发展。文献[18]采用优化BP(back propagation)神经网络方法解决目标评估问题，取得了较好的评估结果，但是普通的BP神经网络理论存在一些不可避免的的缺陷，如过学习、局部极值以及推广能力差等。灰色系统理论，是由我国学者邓聚龙教授首创的一种系统科学理论。它是一种研究少数据、贫信息、不确定性问题的一种新方法。灰色建模要求的样本点少，分布规律要求不高，神经网络具有并行计算、分布式信息存储、自适应学习功能等优点，本文将两者融合起来，建立灰色神经网络(grey neural networks model,GNNM)，可充分弥补单纯使用灰色模型和单纯使用神经网络的不足。GNNM的性能取决于网络的权值和阈值，因此合理选择网络初始参数十分重要。粒子群算法(particle swarm optimization,PSO)是一种群体智能优化算法，它具有搜索速度快、效率高等优点，但是基本粒子群算法存在容易陷入局部最优解的缺点，所以本文借鉴模拟退火算法(simulated annealing,SA)中的概率突跳能力，使粒子跳出已搜索的最优区域，在更大空间中开展搜索。

基于以上分析，本文采用模拟退火粒子群算法修正灰色神经网络的初始参数，使网络输出不断逼近期望输出，并在此基础上建立了基于SAPSO-GNNM目标威胁估计模型。

1灰色神经网络算法原理

1.1灰色理论

灰色模型(grey model,GM)是以原始数据序列为基础建立的微分方程。灰色建模中最有代表性的

模型是针对时间序列的GM建模，它直接将时间序列数据转化为微分方程，利用系统信息，使抽象的模型量化，进而在缺乏系统特性知识的情况下预测系统输出[14]。

GM模型首先对原始数据序列做一次累加，使累加后的数据呈现一定规律，然后用典型曲线拟合该曲线。设有时间数据序列:

(1)

对x(0)做一次累加得到新的数据序列x(1)，新的数据序列x(1)第t项为原始数据序列x(0)前t项之和，即

(2)

根据新的数据序列x(1)，建立白化方程，即

(3)

该方程的解为

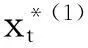
(4)

1.2灰色神经网络

n个参数的灰色神经网络模型的微分方程表达式为

(5)

式中，y2,y3,…,yn为系统输入参数；y1为系统输出参数；a,b1,b2,…,bn-1为微分方程系数。

(5)式的时间响应式为

z(t)=

(6)

(7)

将变化后的式映射到一个扩展的BP神经网络中就得到n个输入参数、1个输出参数的灰色神经网络，其网络拓扑结构如图1所示。

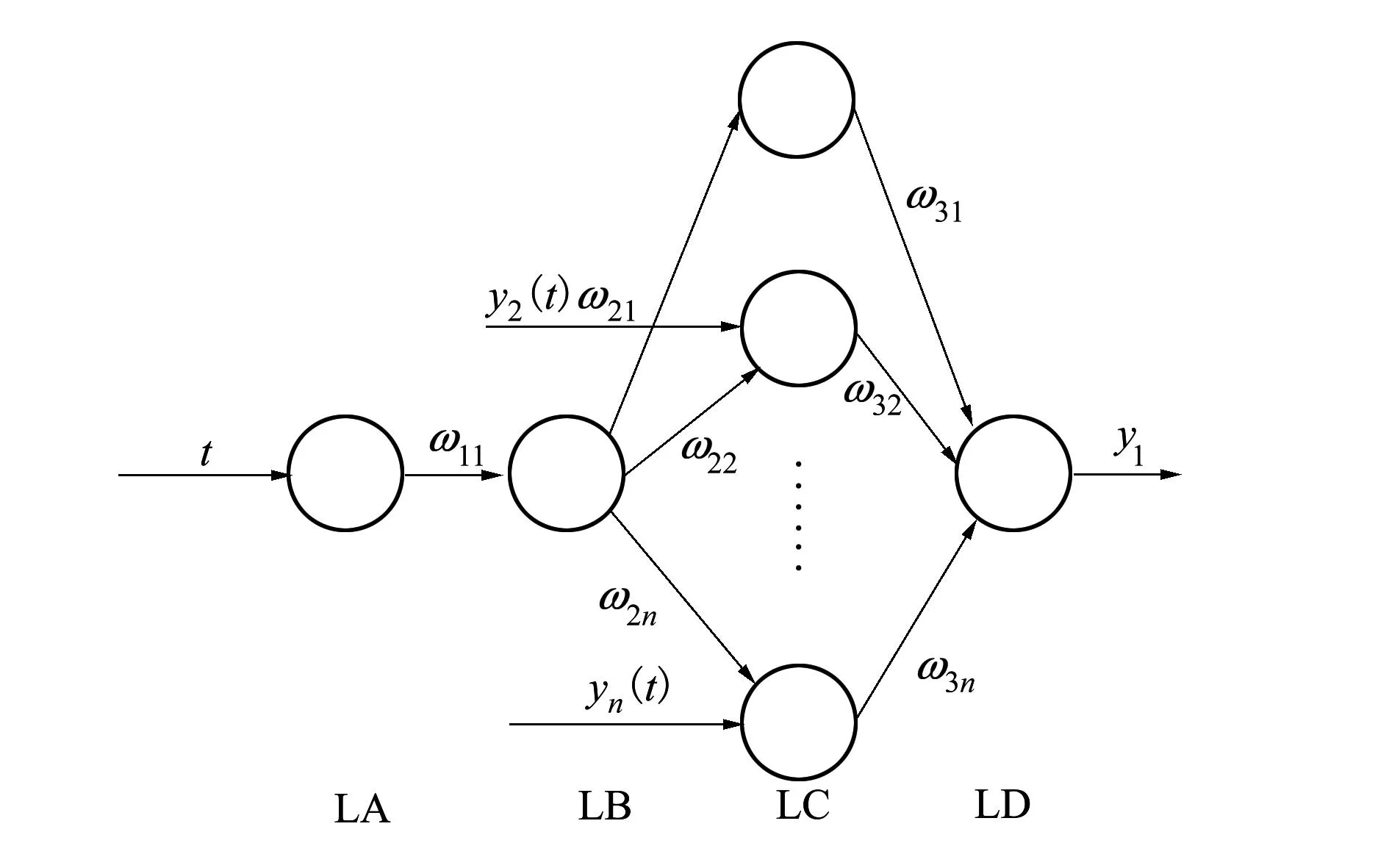
图1　灰色神经网络拓扑结构

2基本粒子群算法

PSO(particle swarm optimization)算法源于对鸟类捕食行为的研究，鸟类捕食时，每种鸟找到食物最简单有效的方法就是搜寻当前距离食物最近的鸟的周围区域[15-17]。

设在一个N维的目标搜索空间中，有n个粒子组成一个种群X=(X1,X2,X3,…,Xn)，其中第i个粒子表示为一个D维的向量Xi=(xi1,xi2,xi3,…,xin)T，i=1,2,…,n,代表第i个粒子在N维搜索空间中的位置，亦代表问题的一个潜在的解。将Xi代入一个目标函数就可以算出其适应值，根据适应值得大小衡量解的优劣。第i个粒子的飞翔速度为Vi=(Vi1,Vi2,Vi3,…,ViD)T。其个体极值为Pi=(Pi1,Pi2,Pi3,…,PiD)T，种群的全局极值Pg=(Pg1,Pg2,Pg3,…,PgD)T。

在每一次迭代过程中，粒子通过个体极值和全局极值更新自身的速度和位置，更新公式如下：

(8)

(9)

式中，k为当前迭代次数；c1和c2为非负的常数，称为学习因子或加速常数，r1和r2为0～1之间的随机数。

3模拟退火改进的PSO算法

模拟退火的基本思想是：用热力学系统来模拟求解的优化问题，把系统的能量看成优化问题的目标函数，用系统逐步降温以达到最低能量状态的退火过程来模拟优化过程。SA算法在搜索过程中具有概率突跳能力，能够有效地避免搜索过程陷入局部极小解。理论已经证明，SA算法在一定条件下以概率1收敛于全局最优解。

基于模拟退火的粒子群算法采用带压缩因子的PSO优化算法，因为带压缩因子的PSO优化算法通过选取合适参数，可确保PSO算法的收敛性，并可取消对速度边界限制。速度和位置更新公式如下：

(10)

(11)

将公式(10)改写为

(12)

性能好的pi应该被赋予较高的选中概率。借用SA算法的机制，认为pi是比pg差的特殊解，从而可计算温度t时pi相对pg的突跳概率，即e-(fp1-fpg)/t，其中f表示目标函数值。如果将此突跳概率值当作pi的适配值，则用pi替代pg的概率。

突跳概率，即e-(fp1-fpg)/t，可按(13)式计算：

(13)

式中，N为种群大小。

算法寻优步骤如下：

1)初始化微粒的位置和速度。

2)计算种群中每个微粒的目标函数值。

3)更新微粒的pbest和gbest。

4)重复执行下列步骤。

①对微粒的pbest进行SA邻域搜索。

②更新各微粒的pbest。

③执行最优选择操作，更新种群gbest。

④gbest是否满足算法终止条件？若是，则转步骤4)，否则转步骤5)。

5)输出种群最优解。

4SAPSO优化的灰色神经网络

SAPSO优化灰色神经网络分为灰色神经网络结构确定、SAPSO搜索算法优化和灰色神经网络预测3个部分。其中灰色神经网络结构确定部分根据样本输入输出参数确定灰色神经网络的结构，进而确定待优化的网络参数，网络参数个数即为粒子群优化算法的个体维数。把个体对应灰色神经网络预测误差作为个体适应度值，SAPSO算法通过种群寻优、SA邻域搜索、最优选择找到最优个体。灰色神经网络预测用SAPSO算法得到的最优个体对网络参数赋值，网络经训练后预测结果输出。具体算法步骤如下：

1) 对初始数据归一化，再对数据进行累加。

2) 网络初始化，对SAPSO算法的加速系数,最大迭代步数，种群规模，速度范围，模拟退火降温常数进行初始设定。

3) 根据输入输出样本确定灰色神经网络结构，并依据网络结构确定待优化的网络参数，网络参数个数即为粒子维度。

4) 种群初始化，随机产生sizepop个初始种群，用训练数据训练灰色神经网络后预测系统输出，把预测输出和期望输出之间的误差绝对值和E作为个体适应度值F，计算公式为

(14)

式中,n为测试集个数;Xi为测试集真实值；Oi测试集预测值；k为系数。

5) 根据(9)式和(12)式更新粒子的位置和速度，重复执行SA领域搜索，最优选择，计算适应度值。

6) 粒子适应度值比较，保留最优个体。

7) 把SAPSO搜索出来的最优个体赋给灰色神经网络，进行下一步的计算和结果输出。

5基于SAPSO灰色神经网络的目标威胁评估建模与仿真

空中目标威胁评估需要考虑多重因素的影响，比如保护目标所处的天气情况、地理环境、经济地位等方面，还有我方雷达设备的情报获取能力和机载或地面武器的空防能力。

5.1目标威胁估计的主要因素

本文主要考虑目标的空防态势来建立空中目标威胁估计模型，采用目标类型、干扰能力、目标高度、目标距离、目标速度和目标航向角6个主要性能指标建立SAPSO-GNNM目标威胁估计模型。

选用目标威胁数据库[18]中的75组作为训练和测试数据，部分数据见表1。选取其中60组数据作为训练集，剩下15组作为测试集，为了适应灰色神经网络模型，在原始数据输入网络之前，需要对数据进行预处理，对各因素进行量化和归一化，目标威胁评估因素量化和归一化计算方法和依据[10-13]:

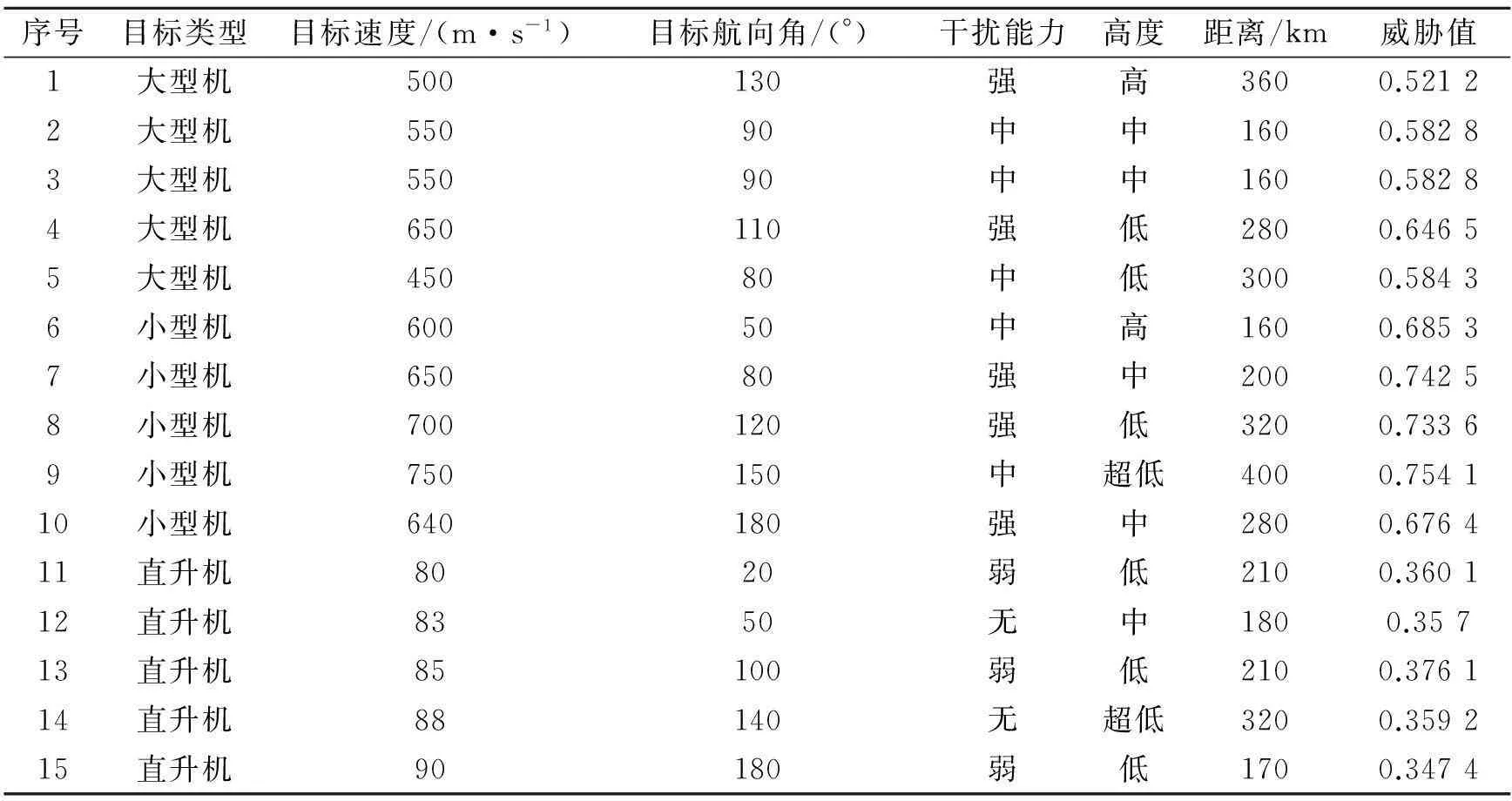
表1　部分目标威胁数据库数据

1) 目标类型：根据目标特征及其威胁程度分为5类：TBM、大型机、小型机、直升机和导弹等。以Miller的人类认知理论为量化依据，对各目标类型隶属度分别依次赋值为0.5、0.4、0.3、0.2、0.1；

2) 目标干扰能力：目标干扰能力越强，防控武器对其命中率越低，威胁程度越大，按干扰能力从强到弱分为5个等级：很强、强、一般、弱、无依次量化为0.9、0.7、0.5、0.3、0.1。

3) 目标航向角：目标航向角决定了目标航路捷径，航路捷径越小，威胁程度越高，其隶属度值从0°～360°等间隔依次量化为0.9、0.8、0.7、0.6、0.5、0.4、0.3、0.2、0.1。

4) 目标高度：空中目标高度越高，我方对其采取措施的时间约充分，所以其威胁程度就越小，目标高度的隶属度值从超低、低、中、高分别量化为0.8、0.6、0.4、0.2。

5) 目标距离：空中目标距离反映了地方的攻击企图和达成攻击的可能性。目标距离越远，威胁程度越小，目标距离的隶属度值由下式等到：

(15)

6) 目标速度：空袭目标速度直接关系到防空武器的系统反映时间和毁伤概率。目标速度越快，其威胁程度越大，目标速度的隶属度值可由下式计算得到：

(16)

5.2模型建立

灰色神经网络构建是根据输入/输出数据维数来确定灰色神经网络的结构。因为目标威胁估计输入数据为6维，输出为一维，所以灰色神经网络结构为1-1-7-1，即LA层为一个节点，输入为序列t，LB层有一个节点，LC层有7个节点，第2～7分别输入目标类型、目标速度、目标航向角、目标干扰能力、目标高度、目标距离6个因素的隶属度数据，输出为预测目标威胁值。粒子群优化算法的惯性权重取0.6，加速因子均取2.05，维数为7，粒子群规模为100，最大迭代步数为100，最小适应值为0.1，速度范围为[-1,1],模拟退火降温常数设为0.5,GNNM的迭代次数设置为200。具体算法流程如图2所示。

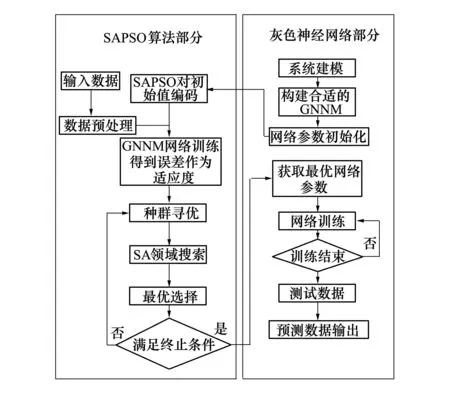
图2　SAPSO-GNNM算法流程图

6仿真结果与验证

因为SAPSO算法粒子的位置和速度初始值是随机的，所有，每一次仿真的结果是不一样的，为验证SAPSO优化的灰色神经网络的性能，本文对所建模型程序运行10次，每次运行都产生15个误差值，其计算结果与测试值得误差绝对值如表2所示。

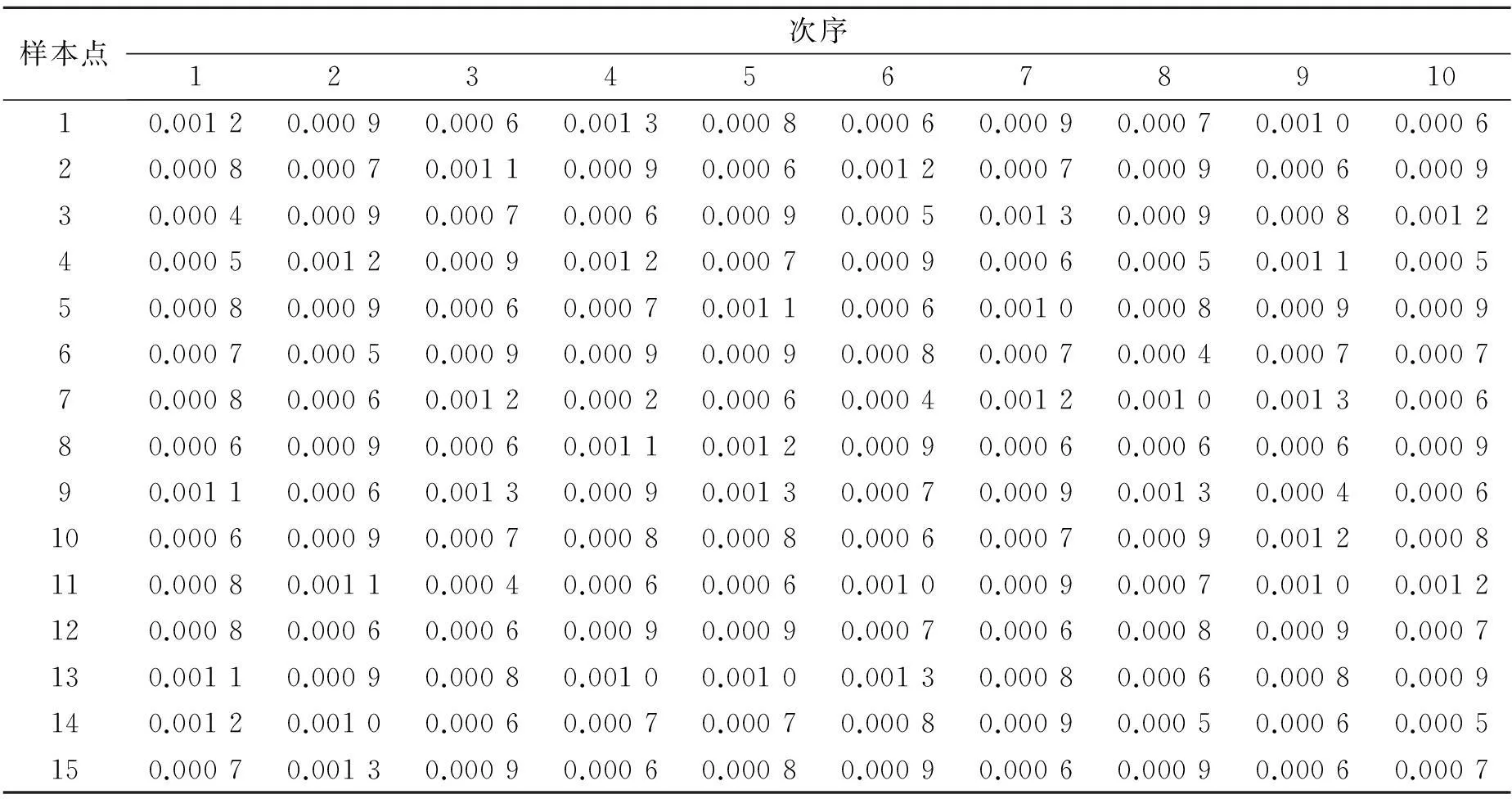
表2　SAPSO-GNNM仿真结果(绝对误差值)

这10次计算误差绝对值的平均值分别是0.000 81、0.000 87、0.000 79、0.000 82、0.000 86、0.000 79、0.000 83、0.000 77、0.000 83、0.000 78。从以上数据可以看出通过SAPSO-GNNM模型预测的结果非常理想，绝对误差值非常小，而且性能稳定。

为了验证基于SAPSO优化的灰色神经网络是否性能上比灰色神经网络和PSO优化的神经网络优越，本文分别用上述3种建模方法进行仿真，其预测的目标威胁值结果见表3。

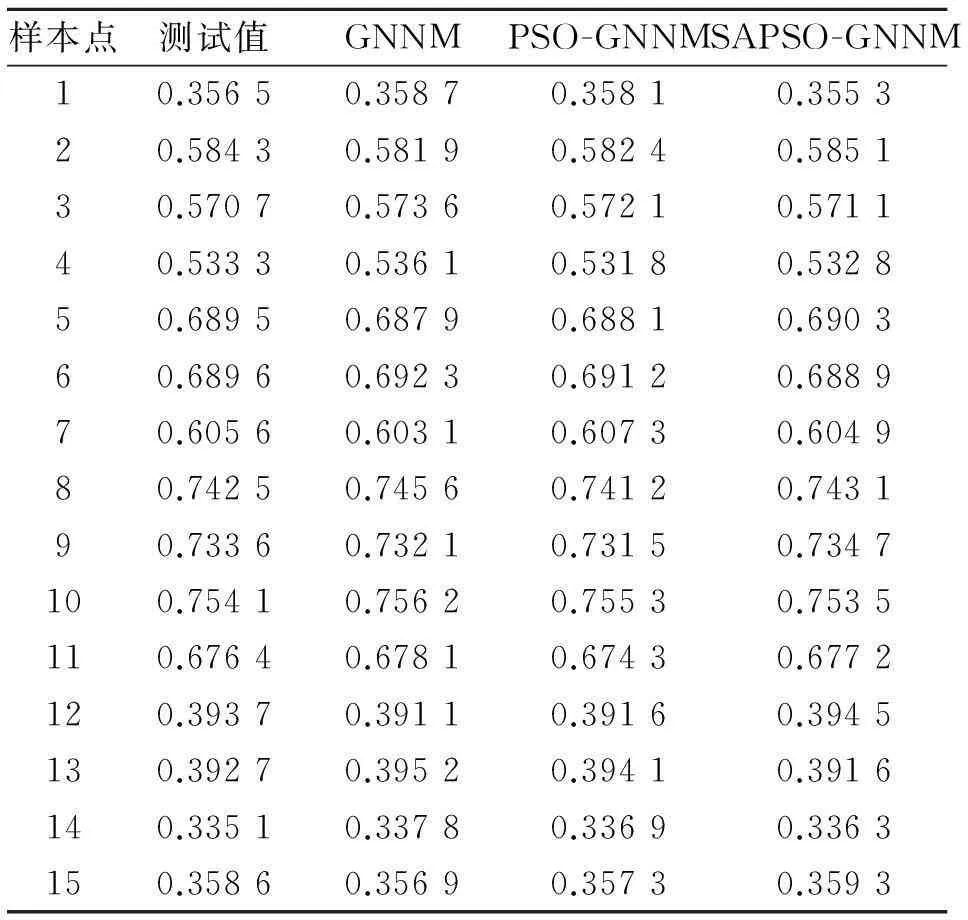
表3　3种模型的仿真结果

绝对误差平均值分别为0.002 3、0.001 6、0.000 8。由于这3种算法预测值与实际值的绝对误差相比测试数据都不算大，所以图3显示3种模型计算出的预测值与测试实际值非常接近，以至于几乎重合。无法看清这3种算法的差别。由图4就可以清晰地看出，GNNM模型预测值与实际威胁值绝对误差最大，而且波动也最大，这说明单纯的灰色神经网络对数据的学习能力较其他2种还是有所欠缺的。虽然PSO-GNNM模型与PSO-GNNM 2种模型预测结果都相对比较稳定，但是基于模拟退火粒子群优化的灰色神经网络目标威胁估计模型计算结果与实际威胁值得绝对误差明显小于其他2种模型。从而近一步验证了SAPSO-GNNM目标威胁估计模型的优越性和准确性。

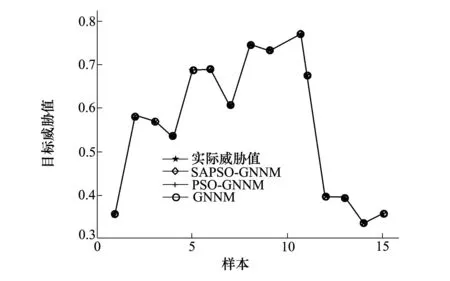
图3　测试集实际威胁值与预测值

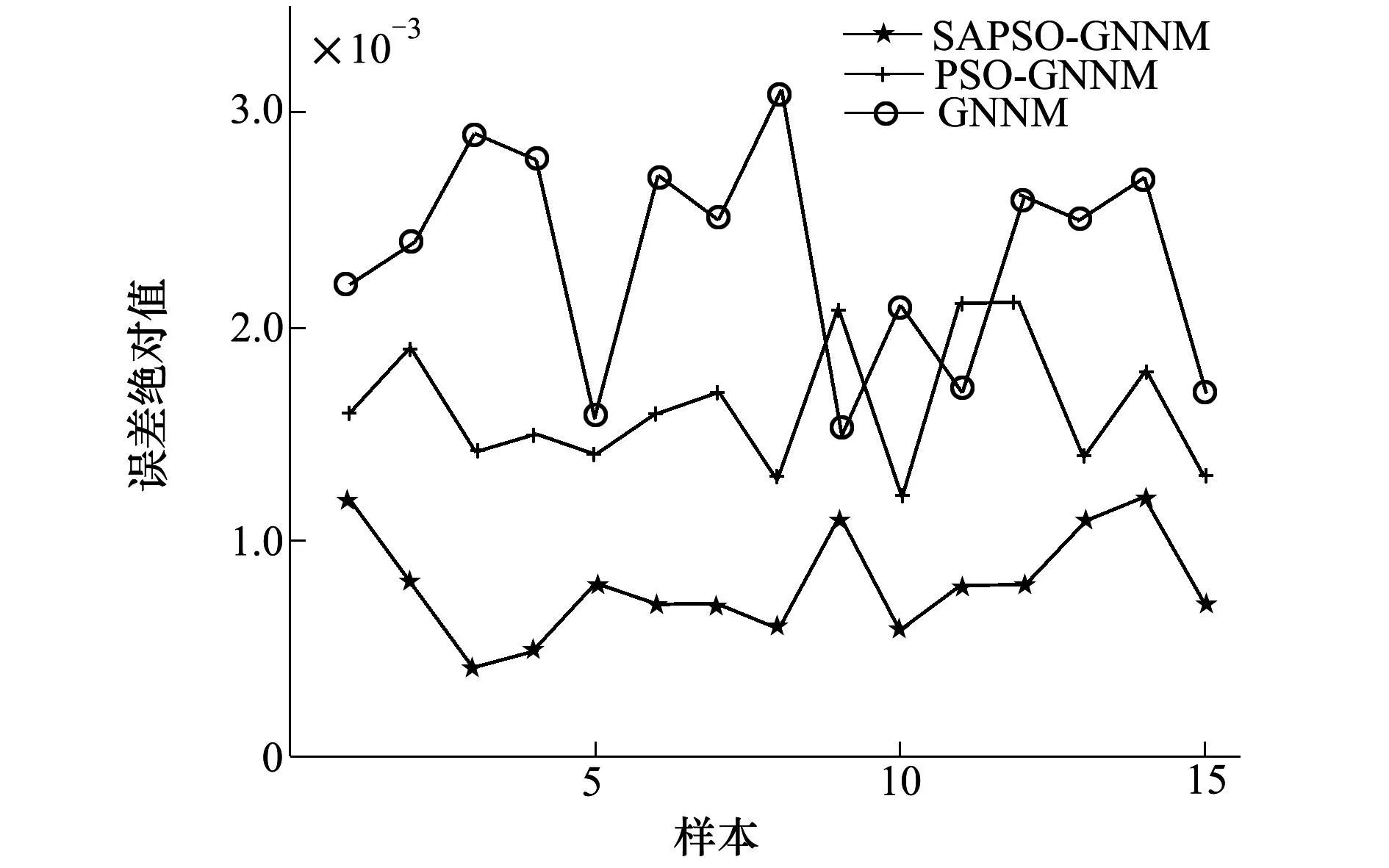
图4　3种估算方法的绝对误差

7结论

空中目标威胁度评估是数据融合需要解决的关键问题之一，考虑目标威胁估计有很多不确定性问题的特点，结合灰色神经网络可以通过对无规律系统已知信息研究，揭示未知信息，并且引入模拟退火、粒子群优化算法，提出了一种基于SAPSO-GNNM的空中目标威胁估计方法，仿真实验结果表明该算法的平均误差远优于GNNM、PSO-GNNM得出的结果，具有优异的预测能力，能够更准确完整地提供空中目标威胁估计。为目标威胁估计提供了科学有效的新途径，为6个目标威胁的主要性能指标与目标威胁度关系提供了一个总体认识。

参考文献：

[1]Wang Y, Miao X. Intuitionistic Fuzzy Perceiving Methods for Situation and Threat Assessment[C]∥Proc of IEEE Int Conf on Fuzzy Systems and Knowledge Discovery Sichuan, 2012: 578-582

[2]雷英杰, 王宝树, 王毅. 基于直觉模糊推理的威胁评估方法[J]. 电子与信息学报, 2007, 29(9): 2077-2081

Lei Yingjie, Wang Baoshu, Wang Yi. Techniques for Threat Assessment Based on Intuitionistic Fuzzy Reasoning[J]. J Electronics & Information Technology, 2007, 29(9): 2077-2081 (in Chinese)

[3]Xu Y, Wang Y, Miu X. Multi-Attribute Decision Making Method for Air Target Threat Evaluation Based on Intuitionistic Fuzzy Sets[J]. J of Systems Engineering and Electronics, 2012, 23(6): 891-897

[4]夏博龄, 贺正洪, 雷英杰. 基于直觉模糊推理的威胁评估改进算法[J]. 计算机工程, 2009, 35(16): 195-197

Xia Boling, He Zhenghong, Lei Yingjie. Improved Algorithm of Threat Assessment Based on Intuitionistic Fuzzy Reasoning[J]. Computer Engineering, 2009, 35(16): 195-197 (in Chinese)

[5]Wang Y, Sun Y, Li J Y, et al. Air Defense Threat Assessment Based on Dynamic Bayesian Network[C]∥Proc of IEEE Int Conf on Systems and Informatics, Yantai, 2012: 721-724

[6]刘跃峰, 陈哨东,赵振宇,等. 基于FBNs的有人机/UCAV编队对地攻击威胁评估[J]. 系统工程与电子技术,2012,34(8):1635-1639

Liu Yuefeng, Chen Shaodong, Zhao Zhenyu, et al. Threat Assessment of Manned/Unmanned Combat Aerial Vehicle Formation Air-to-Ground Attack Based on FBNs[J]. Systems Engineering and Electronics, 2012, 34(8): 1635-1639 (in Chinese)

[7]王小艺, 刘载文, 侯朝桢, 等. 基于模糊多属性决策的目标威胁估计方法[J]. 控制与决策, 2007, 22(8): 859-863

Wang Xiaoyi, Liu Zaiwen, Hou Chaozhen, et al. Method of Object Threat Assessment Based on Fuzzy MADM[J]. Control and Decision, 2007, 22(8): 859-863 (in Chinese)

[8]王宝成, 栗飞, 陈正. 基于模糊TOPSIS法的空袭目标威胁评估[J]. 海军航空工程学院学报, 2012, 27(3): 323-326

Wang Baocheng, Li Fei, Chen Zheng. Air-Attack Targets Threat Assessment Based on Fuzzy TOPSIS[J]. J Naval Aeronautical and Astronautical University, 2012, 27(3):323-326 (in Chinese)

[9]王鑫, 吴华, 赵玉,等. 电子战目标威胁评估的折衷排序方法[J]. 电光与控制, 2013, 20(8): 14-17

Wang Xin, Wu Hua, Zhao Yu, et al. A Compromise Sorting Method for Electronic Warfare Target Threat Assessment[J]. Electronics Optics & Control, 2013, 20(8): 14-17 (in Chinese)

[10] 邢清华, 刘付显. 直觉模糊集隶属度与非隶属度函数的确定方法[J]. 控制与决策, 2009, 24(3): 393-397

Xing Qinghua, Liu Fuxian. Method of Determining Membership and Nonmembership Function in Intuitionistic Fuzzy Sets[J]. Control and Decision, 2009, 24(3): 393-397 (in Chinese)

[11] Miller G A. The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information[J]. Psychological Review, 1956, 63(2): 81-97

[12] 孙海永, 陈阳晔, 韩会刚. 基于灰色聚类的空袭目标威胁评估与排序[J]. 空军雷达学院学报, 2011, 25(5): 355-357

Sun Haiyong, Chen Yangye, Han Huigang. Assessing and Ranking of Air-Raid Target Threat Based on Grey Clustering[J]. Journal of Air Force Radar Academy, 2011, 25(5): 355-357 (in Chinese)

[13] 武华，苏秀琴. 基于群广义直觉模糊软集的空袭目标威胁评估方法[J]. 控制与决策,2015，30(8)：1462-1467

Wu Hua, Su Xiuqin. Threat Assessment of Aerial Targets Based on Group Generalized Intuitionistic Fuzzy Soft Sets[J]. Control and Decision, 2015, 30(8): 1462-1467 (in Chinese)

[14] 邓聚龙. 灰色系统基本方法[M]. 武汉：华中科技大学出版社，2005: 38-42

Deng Julong. The Primary Methods of Grey System Theory[M]. Wuhan: Huazhong University of Science and Technology Press,2005: 38-42 (in Chinese)

[15] Kennedy Jeberhart R. Particle Swarm Optimization[C]∥Proceedings of the IEEE International Conference on Neural Networks,1995(4):1942-1948

[16] Eberhart T, Kennedy J. A New Optimizer Using Particle Swarm Theory[C]∥Proceedings of the Sixth International Sympsoium on Micro Machine and Human Science,1995: 39-43

[17] Eberhart R C, Shi Y H. Particle Swarm Optimization: Decelopments, Applications and Resources[C]∥Proceedings of the IEEE Conference on Evolutionary Computation, 2001(1):81-86

[18] 王改革. 基于智能算法的目标威胁估计[D]. 长春:中国科学院长春光学精密机械与物理研究所, 2013: 67-71

Wang Gaige. Target Threat Assessment Using Intelligence Algorithms[D]. Changchun: Changchun Institute of Optics, Fine Mechanics and Physics Chinese Academy of Sciences, 2013: 67-71

Target Threat Assessment Using SAPSO and Grey Neural Network

Liu Haibo1, Wang Heping1,2, Shen Liding1

(1．College of Aeronautics，Northwestern Polytechnical University，Xi'an 710072，China 2．Shenzhen Research Institute of Northwestern Polytechnical University，Shenzhen 518057，China )

Abstract:According to the characteristics of target threat estimation has a lot of uncertainty, Analyzed the defects of traditional target threat estimation method and gray neural network (GNNM) initial parameters randomly selected. Using simulated annealing (SA) improved particle swarm optimization (PSO) algorithm to search for the optimal values of initial parameters of network, The establishment of a simulated annealing particle swarm algorithm to optimize the gray neural network model, Improved the robustness and accuracy of prediction model. Comparing with GNNM and PSO-GNNM, The simulation results show that SAPSO-GNNM has good prediction ability, Have the ability to accurately estimate air targets threat Can be accurately estimated air targets threat.

Keywords:backpropagation algorithms, computer simulation, differential equations, eigenvalues and eigenfunctions, errors, estimation, flowcharting, forecasting, mathematical models, membership functions, neural networks, optimization, particle swarm optimization (PSO), probability, regression analysis, simulated annealing, temperature, time series, topology, GNNM(Grey Neural Networks Model), grey system, SAPSO(simulated annealing particle swarm optimization), Target threat optimization.

中图分类号：TP391.9

文献标志码：A

文章编号:1000-2758(2016)01-0025-08

作者简介：刘海波(1981—)，西北工业大学博士研究生，主要从事智能算法与飞行器控制系统研究。

基金项目：深圳市科技研发基金(CXZZ20120831170042239)资助

收稿日期：2015-04-25