考虑弹流润滑效应的高速角接触球轴承刚度特性研究

余永健, 陈国定, 李济顺

(1.西北工业大学 机电学院, 陕西 西安　710072; 2.河南省机械设计及传动系统重点实验室, 河南 洛阳　471003)



考虑弹流润滑效应的高速角接触球轴承刚度特性研究

余永健1, 陈国定1, 李济顺2

(1.西北工业大学 机电学院, 陕西 西安710072; 2.河南省机械设计及传动系统重点实验室, 河南 洛阳471003)

摘要：高速角接触球轴承的刚度特性对航空发动机转子系统的动态特性有着重要影响。为获得油润滑条件下角接触球轴承刚度特性,需要考虑弹流润滑效应对轴承刚度的影响。基于Jones拟静力学模型,建立了考虑弹流润滑影响的耦合滚动体/套圈接触刚度和油膜刚度的滚动轴承刚度计算模型。应用滚动轴承刚度计算模型分析了弹流润滑效应对角接触球轴承刚度的影响规律。研究结果表明:与不考虑弹流润滑效应的情况相比,考虑弹流润滑效应的角接触球轴承刚度有较明显的降低;较之轴承轴向刚度,轴承径向刚度对弹流润滑效应更为敏感;在考虑弹流润滑效应的情况下,润滑油动力黏度和黏压系数的增大均使得轴承刚度减小,黏温系数的增大仅使得轴承径向刚度增大,但对轴向刚度几乎没有影响;随着转子转速的升高,弹流润滑效应对轴承径向刚度的影响愈加明显,但对轴向刚度的影响逐渐弱化;随着轴向载荷的增加,弹流润滑效应对轴承刚度的影响缓慢增大;随着径向载荷的增加,弹流润滑效应对轴向刚度的影响缓慢减小,而对径向刚度的影响则几乎保持不变。

关键词：高速球轴承;弹流润滑效应;接触刚度;油膜刚度;轴承刚度

高速滚动轴承是高速旋转主轴的关键元件,广泛应用于航空航天领域,其DN值大于0.6×106mm·(r/min)。高速滚动轴承刚度直接影响着主轴转子系统的稳定性和动态性能[1],是主轴转子系统的关键参数。当主轴转子系统的共振频率与其所受的激励频率相近时,转子系统将产生强烈振动,导致主轴转子系统的损坏。因此,精确计算滚动轴承刚度,为主轴转子系统合理设计提供参数依据,保证主轴转子系统运行时的可靠性和稳定性,是十分重要的。

有关滚动球轴承的刚度分析,国内外学者已进行了广泛研究。Jones等通过其提出的滚动轴承拟静力学模型[2-4],根据滚动控制理论分析了离心力和陀螺力矩对轴承刚度的影响;文献[5-9]基于Jones拟静力模型和Hertz接触理论,建立了角接触球轴承的刚度计算模型,考虑了轴承过盈量、离心膨胀和轴承温升导致的内圈径向变形,研究了这些因素对角接触球轴承刚度的影响;袁幸等建立了考虑内外圈表面波纹度的滚动轴承拟静力学模型,计算了考虑波纹度的轴承刚度[10];黄浩等建立了角接触球轴承拟静力学模型,在轴承几何相容方程中考虑了油膜厚度的影响,分析了主轴转速和载荷对轴承刚度的影响[11];Kang等把轴承的几何尺寸和工况参数与角接触球轴承的刚度之间复杂的函数关系通过神经网络来表征,从而计算出轴承刚度[12];文献[13-14]基于Jones拟静力学模型和Hertz接触理论,对轴承刚度进行了计算;Guo等利用有限元软件建立了滚动轴承的有限元模型,计算了各类滚动轴承的刚度[15],但没有考虑离心力和润滑等的影响。Hagiu等建立了高速轴承动力学模型,给出了轴承的刚度计算方法,其中考虑了进油口油膜刚度和接触区油膜刚度的影响[16]。

纵观已有轴承刚度计算的研究工作,大多数的研究没有考虑弹流润滑效应的影响,仅有个别文献

的分析虽考虑了润滑因素,或仅是在滚动轴承力学模型的几何相容方程中考虑了油膜厚度,以此形式将润滑影响反映到轴承刚度的计算中;或是通过经典的Hamrock-Dowson弹流润滑油膜厚度公式计算出弹流油膜刚度,并将其嵌入到轴承刚度计算模型中。由于滚动体/套圈间的油膜厚度影响轴承载荷分布,进而影响滚动体/套圈的接触刚度,而轴承载荷分布又反过来影响油膜厚度的大小,进而影响到油膜刚度大小,但迄今同时包含考虑油膜厚度影响的滚动体/套圈接触刚度和油膜刚度在内的滚动轴承刚度计算模型和方法尚未见报道,亦即现有的滚动轴承刚度计算难以反映轴承实际刚度。

本文以Jones拟静力学模型为基础,建立了基于油膜厚度影响的轴承几何相容方程,提出了考虑油膜厚度影响的钢球/套圈接触刚度计算模型,通过计入弹流油膜刚度形成了钢球与套圈的等效刚度,并最终提出了滚动轴承径向刚度和轴向刚度的计算公式。基于上述计算流程开展了球轴承刚度分析,探讨了润滑油性能参数(动力黏度、黏温系数和黏压系数)、主轴转速和载荷对球轴承刚度的影响规律,以体现弹流润滑效应对球轴承刚度的影响。

1滚动球轴承刚度计算模型

基于考虑油膜厚度的滚动轴承拟静力学模型,计算钢球/套圈的接触刚度和油膜刚度,把钢球/套圈的接触刚度与油膜刚度串联,从而计算出钢球/套圈的等效刚度,结合Harris轴承刚度计算方法,最终获得滚动轴承的轴向刚度和径向刚度。

1.1钢球/套圈的接触刚度

图1所示为滚动球轴承任意位置处的钢球(定义为第q个钢球)球心与内外沟道曲率中心受载前后的位置关系。图1中n点表示外沟道曲率中心,分析中假设其固定不动。滚动轴承旋转时,在载荷、离心力和陀螺力矩共同作用下,内沟道曲率中心由受载前的位置m点移至受载后的m′点,球心则由受载前的位置C点移至受载后的C′点。

对于图1所示的第q个钢球,考虑钢球与套圈之间的油膜厚度和弹性变形,内外沟道曲率中心与受载后球心之间的距离Δiq和Δeq分别为

(1)

(2)

式中,ri和re分别为内圈沟道曲率半径和外圈沟道曲率半径;Dw为钢球直径;δiq和δeq分别为第q个钢球与内圈和外圈之间的弹性变形;hicq和hecq分别为第q个钢球与内圈接触区域、外圈接触区域的中心油膜厚度。

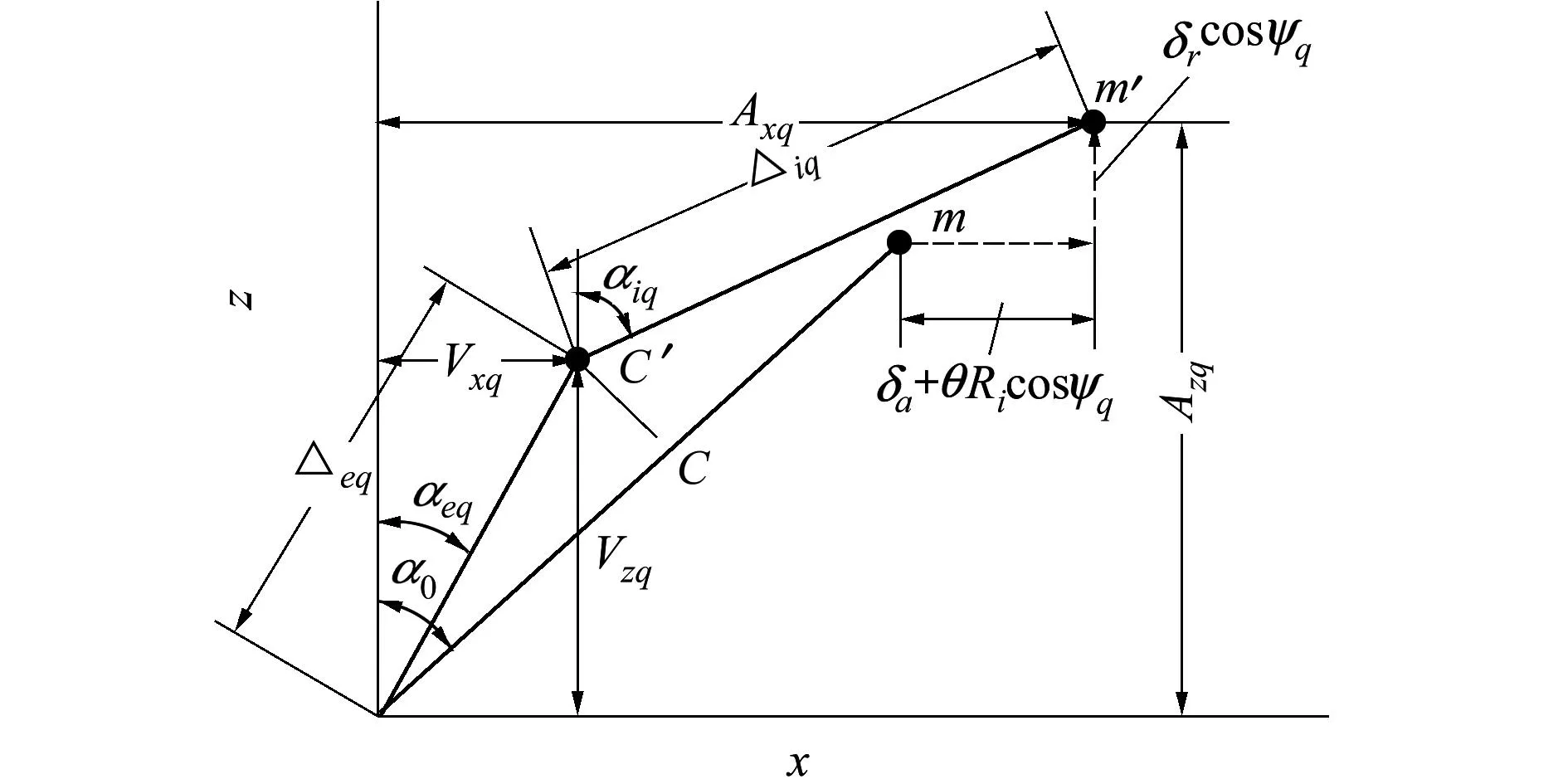
图1　任意位置钢球球心与内外沟道曲率中心相对位置

受载后内沟道曲率中心的坐标为

(3)

(4)

式中：Ri=dm/2+(fi-0.5)Dwcosα0,B=fi+fe-1,其中,fi、fe分别为内、外圈的沟曲率半径系数;ψq为第q个钢球的位置角;θ为轴承内圈的倾角;δa为轴承内圈轴向位移量;δr为轴承内圈径向位移量;α0为受载前的接触角。

由公式(1)～(4),结合图1所表示的几何关系,考虑油膜厚度的变形几何相容方程可表示为

(5)

(6)

图2　钢球受力图

根据图2所示的第q个钢球的受力情况,钢球的受力平衡方程为

(7)

(8)

式中,Qiq和Qeq分别为钢球/内圈、钢球/外圈的接触法向上的载荷;Mgq为钢球承受的陀螺力矩;Fcq为钢球承受的离心力;αiq和αeq分别为钢球与内圈的接触角和钢球与外圈的接触角;λiq和λeq分别为内圈和外圈的修正系数。

当轴承承受轴向力Fa和径向力Fr时,轴承内圈的受力平衡方程为

(9)

(10)

公式(5)～公式(10)构成了一个非线性方程组,在已知轴承几何参数和工况参数的条件下,求解此方程组可以获得轴承的载荷分布,并进而获得每个钢球/套圈的接触载荷。

根据Hertz接触理论,钢球与套圈之间的接触载荷和弹性变形关系为[17]

(11)

式中,E、F分别为第一类完全椭圆积分和第二类完全椭圆积分;∑ρ为钢球/套圈接触点主曲率和;k为钢球/套圈椭圆接触率;E′为钢球/套圈的等效弹性模量;Q为钢球/套圈的接触载荷。

对方程(11)中的Q关于δ求导,可得钢球与套圈的接触刚度为

(12)

1.2钢球/套圈的油膜刚度

钢球/套圈的油膜刚度是根据钢球/套圈接触载荷与接触区最小油膜厚度的关系推导出来的。如果认为钢球/套圈之间的润滑状态是弹性流体动压润滑状态,则考虑热效应弹流润滑最小油膜厚度公式为[18-19]

(13)

式中:P0为钢球与套圈的最大接触压应力;S为钢球与套圈接触点的滑滚比;L为热承载系数,L=βη0u2/λ,β为润滑油的黏温系数;E′为钢球与套圈的等效弹性模量;k为钢球与套圈的椭圆接触率;η0是润滑油在大气压下的动力黏度;Rx是当量曲率半径;u是接触点卷吸速度;α是润滑油黏压系数;λ为润滑油的热导率。

对方程(13)中的Q关于hmin求导,从而计算出钢球/套圈间的油膜刚度,即

(14)

1.3钢球/套圈的等效刚度

钢球/套圈的等效刚度是其接触刚度与油膜刚度的串联,这样,第q个钢球与套圈的等效刚度表示为

(15)

根据Harris推导的滚动轴承等效刚度计算公式,第q个钢球与套圈的等效刚度在径向和轴向上的刚度分量分别为[20]

(16)

(17)

式中,αq为第q个钢球与套圈的受载后的接触角。

对于滚动轴承而言,其轴向刚度和径向刚度可以通过每一个钢球/套圈的等效刚度叠加而获得,即表示为[22]

(18)

(19)

式中:Ka和Kr分别为轴承的等效轴向刚度和等效径向刚度;Kr-iq和Ka-iq分别为第q个钢球与内圈的径向等效刚度和轴向等效刚度;Kr-eq和Ka-eq分别为第q个钢球与外圈的径向等效刚度和轴向等效刚度;Z为钢球的个数。

2计算结果及分析

本文算例高速角接触球轴承的主要结构及润滑参数为:外沟道曲率系数为0.515,内沟道曲率系数为0.52,轴承节圆直径为168.4 mm,钢球直径为22.225 mm,钢球个数为20;润滑油参数为:动力黏度为0.036 4 Pa·s,黏压系数为1.85×10-8Pa-1,黏温系数为0.031 5 ℃-1。

2.1润滑油动力黏度对球轴承刚度的影响

图3给出了内圈转速为10 000 r/min、轴向载荷为10 000 N和径向载荷为4 000 N时,润滑油动力黏度对轴承轴向刚度和径向刚度的影响。由图3可以看出,在考虑弹流润滑效应的情况下,润滑油动力黏度的增大使轴承轴向和径向刚度都呈现出减小的趋势。当润滑油动力黏度增大时,钢球与套圈间的油膜厚度增大,从而使油膜刚度减小,进而使钢球与套圈的等效刚度减小,最终使轴承的轴向和径向刚度减小。

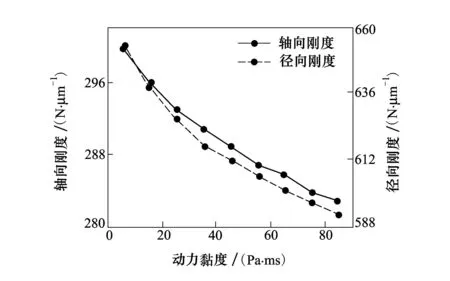
图3　动力黏度对轴承刚度的影响

2.2润滑油黏温系数对球轴承刚度的影响

图4给出了内圈转速为10 000 r/min、轴向载荷为10 000 N和径向载荷为4 000 N时,润滑油黏温系数对轴承轴向刚度和径向刚度的影响。

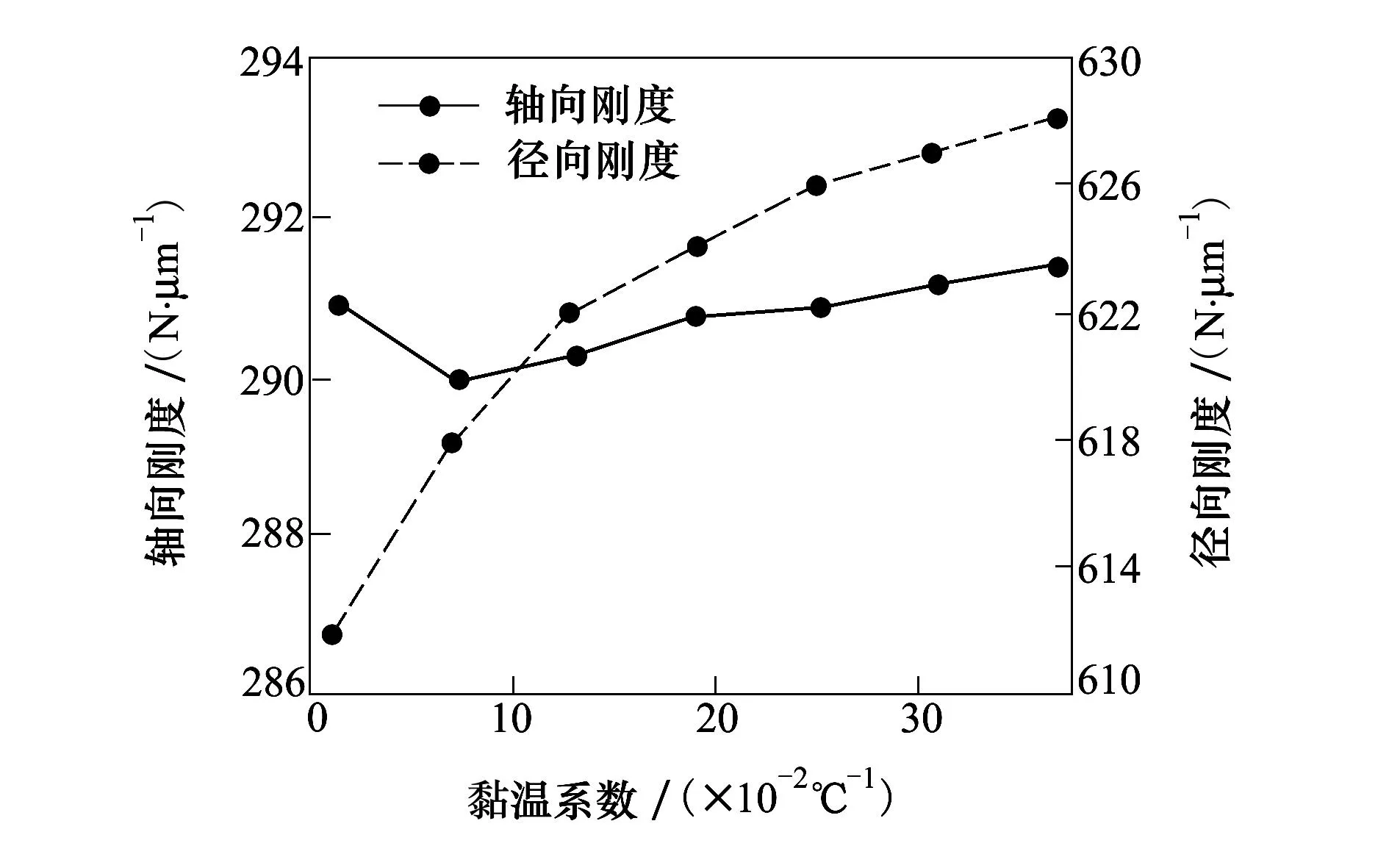
图4　黏温系数对轴承刚度的影响

由图4可以看出,随着润滑油黏温系数的增大,弹流润滑效应对轴承轴向刚度影响很小,而径向刚度则呈现出逐渐增大的趋势。这是因为润滑油黏温系数的增大使钢球与套圈间油膜厚度减小,从而导致钢球与内圈接触角减小,同时使钢球与套圈等效刚度增大,上述2个因素的共同作用使得径向刚度随着黏温系数的增大而明显增大,而使轴向刚度随着黏温系数的增大而变化较小。

2.3润滑油黏压系数对球轴承刚度的影响

图5给出了内圈转速为10 000 r/min、轴向载荷为10 000 N和径向载荷为4 000 N时,润滑油黏压系数对轴承轴向刚度和径向刚度的影响。由图5可以看出,随着润滑油黏压系数的增大,弹流润滑效应使轴承轴向和径向刚度均呈现出近似直线的下降趋势。这是由于黏压系数的增大使钢球与套圈间油膜厚度增大,从而使钢球与套圈间等效刚度减小,进而使轴承轴向刚度和径向刚度随之减小。

图5　黏压系数对轴承刚度的影响

2.4主轴转速对球轴承刚度的影响

图6给出了轴向载荷为10 000 N和径向载荷为4 000 N下主轴转速对轴承轴向刚度和径向刚度的影响。图6中可以看出,随着主轴转速的增加,轴向刚度先迅速减小后又逐渐趋于稳定,而对径向刚度的影响则是逐渐增大。与不考虑润滑时计算的轴承刚度相比,考虑润滑后轴向刚度和径向刚度都减小。这是由于钢球与套圈间Hertz接触刚度与油膜刚度串联后的等效刚度小于Hertz接触刚度所导致的结果。图6中还可以看出,径向刚度较轴向刚度对润滑效应敏感。这是由于弹流润滑效应使钢球与套圈接触角增大,同时也使钢球与套圈等效刚度减小,钢球与套圈接触角增大使得等效刚度轴向分量增大,而钢球与套圈等效刚度减小使得等效刚度轴向分量减小,上述2个因素的共同作用使得轴向刚度对润滑效应不敏感;同理,可以解释轴承径向刚度对润滑较敏感。随着转速的增加,弹流润滑效应对轴向刚度的影响越来越小,而对径向刚度的影响则越来越大。

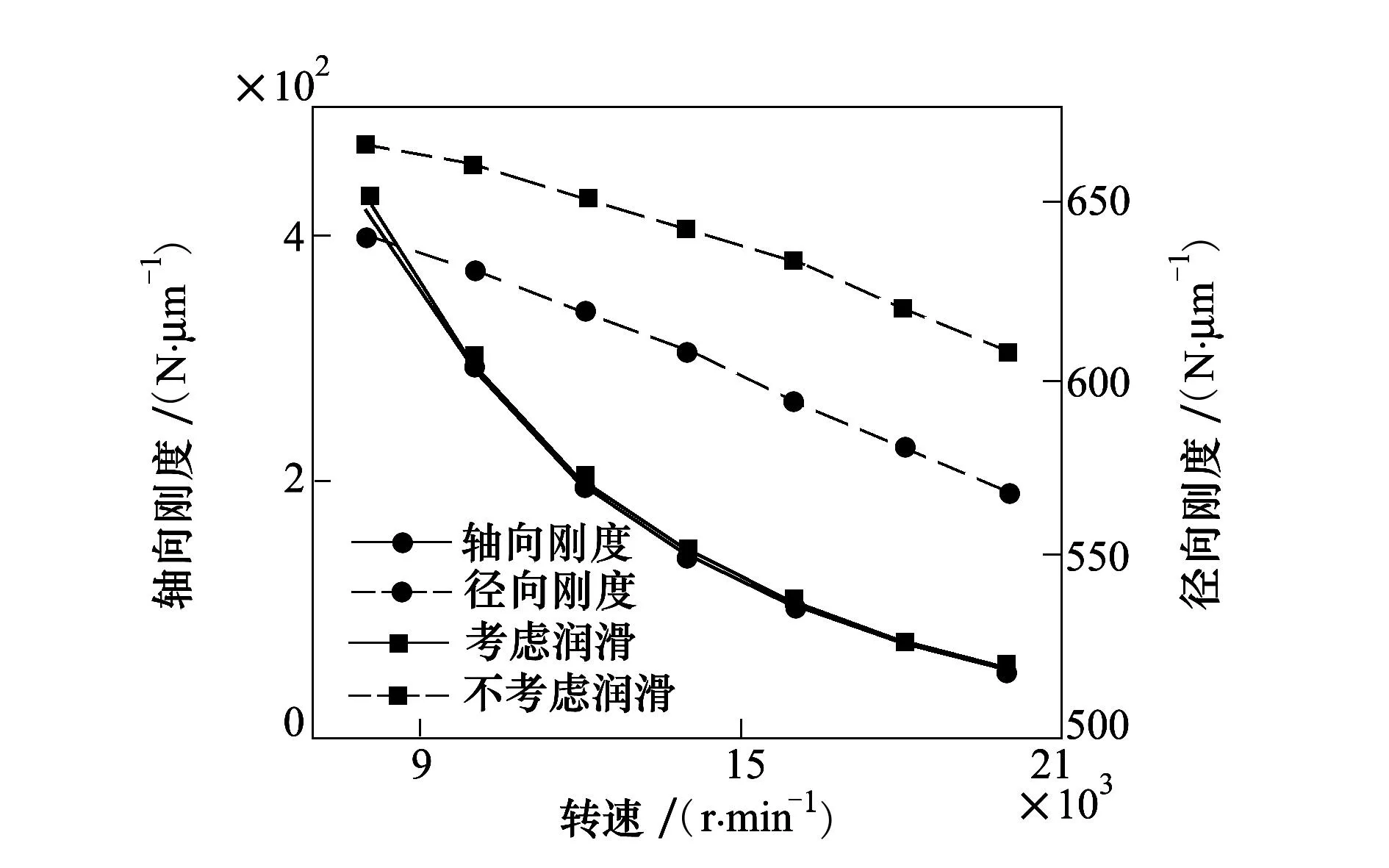
图6　主轴转速对轴承刚度的影响

2.5载荷对球轴承刚度的影响

图7给出了主轴转速为10 000 r/min和径向载荷为4 000 N时,轴向载荷对轴向刚度和径向刚度的影响。图7中可以看出,轴向刚度和径向刚度都随着轴向载荷的增加而逐渐增大。与不考虑润滑时的轴承刚度相比,随着轴向载荷的增加,弹流润滑效应对轴承刚度的影响缓慢增大,且弹流润滑效应对径向刚度较轴向刚度敏感。这是由于弹流润滑效应使钢球与套圈间的等效刚度减小,同时使钢球与套圈接触角增大,两者共同作用使弹流润滑效应对径向刚度较轴向刚度影响大。

图7　轴向载荷对轴承刚度的影响

图8给出了在主轴转速为10 000 r/min和轴向载荷为10 000 N时,径向载荷对轴向刚度和径向刚度的影响。图8中可以看出,轴向刚度随着径向载荷的增加而减小,而径向刚度则随之逐渐增大。与不考虑润滑时的轴承刚度相比,随着径向载荷的增加,弹流润滑效应对轴向刚度的影响缓慢减小,而对径向刚度的影响则几乎保持不变,且弹流润滑效应对径向刚度较轴向刚度敏感。这是由于弹流润滑效应使钢球与套圈间的等效刚度减小,同时使钢球与套圈接触角增大,两者共同作用使弹流润滑效应对径向刚度较轴向刚度影响大。

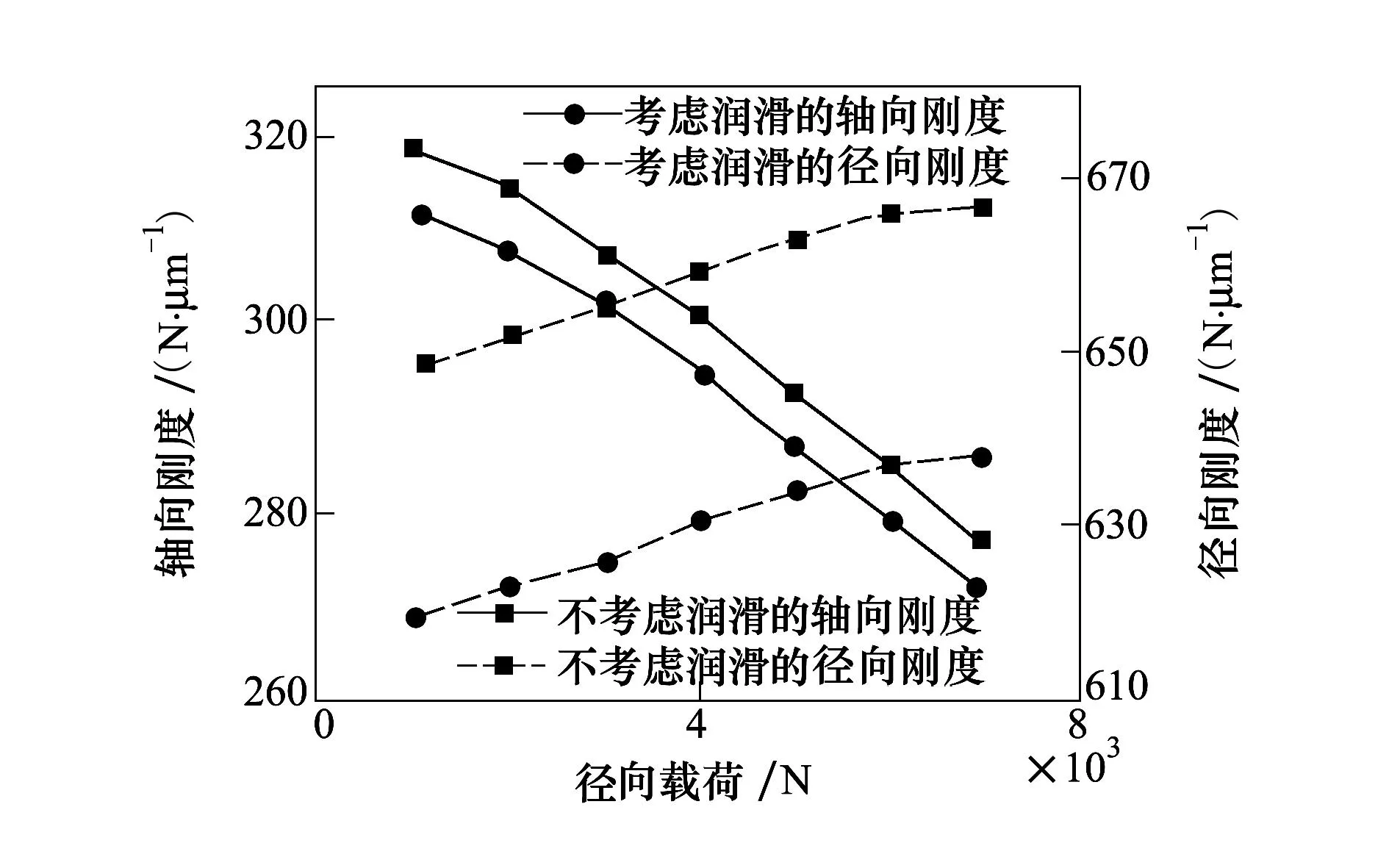
图8　径向载荷对轴承刚度的影响

由图7和图8可以看出,润滑效应对轴承径向刚度影响较大,对轴承径向刚度影响较小。

3结论

本文给出了计及轴承钢球/套圈间润滑油膜和油膜刚度,建立了基于弹流润滑的球轴承刚度计算方法,分析了润滑油动力黏度、黏温系数和黏压系数对球轴承刚度的影响,同时还分析了不同工况参数下弹流润滑对球轴承刚度的影响,其主要结论如下:

1) 在考虑弹流润滑效应的情况下,润滑油动力黏度和黏压系数的增大均使得轴承刚度减小,黏温系数的增大仅使得轴承径向刚度增大,但对轴向刚度几乎没有影响。

2) 与不考虑弹流润滑效应的情况相比,考虑弹流润滑效应的角接触球轴承刚度有较明显的降低;较之轴承轴向刚度,轴承径向刚度对弹流润滑效应更为敏感。

3) 随着转子转速的升高,弹流润滑效应对轴承径向刚度的影响愈加明显,但对轴向刚度的影响逐渐弱化;随着轴向载荷的增加,弹流润滑效应对轴承刚度的影响逐渐增强;随着径向载荷的增加,弹流润滑效应对轴向刚度的影响逐渐减弱,而对径向刚度的影响则几乎保持不变。

参考文献：

[1]Kim S M, Lee K J, Lee S K. Effect of Bearing Support Structure on the High-Speed Spindle Bearing Compliance[J]. International Journal of Machine Tools and Manufacture, 2002,42(3):365-373

[2]Jones A B. The Mathematical Theory of Rolling Elements Bearings[M]. Mechanical Design and Systems Handbook. New York, Mc Graw-Hill, 1966

[3]Jones A B, McGron J M. Rotor-Bearing Dynamics Technology Design Guide. Part2: Ball Bearing[R]. OH: Wright Patterson Air Force Aero Propulsion Lab, AFAPLTR-78-6: 1-62

[4]Jones A B. A General Theory for Elastically Constrained Ball and Radial Roller Bearing[J]. Trans ASME J Basic Eng,1960, 82: 309-320

[5]王硕桂,夏源明. 过盈配合量和预紧力对高速角接触球轴承刚度的影响[J]. 中国科学技术大学学报, 2006,36(12): 1314-1320

Wang Shuogui, Xia Yuanming. Effect of the Interference Fit and Axial Preload in the Stiffness of the High-Speed Angular Contact Ball Bearing[J]. Journal of University of Science and Technology of China, 2006, 36(12): 1314-1320 (in Chinese)

[6]王保民,梅雪松,胡赤兵,等. 内圈离心位移对高速角接触球轴承刚度的影响[J]. 计算力学学报,2010,27(1): 145-150

Wang Baomin, Mei Xueshong, Hu Chibing, et al. Influence of Inner Ring Centrifugal Displacement on the Stiffness of High-Speed Angular Contact Ball Bearing[J]. Chinese Jouranl of Computational Mechanics, 2010,27(1): 145-150 (in Chinese)

[7]曹宏瑞,李兵,陈雪峰,等. 高速主轴离心膨胀及对轴承动态特性的影响[J]. 机械工程学报,2012,48(19): 59-64

Cao Hongrui, Li Bing, Chen Xuefeng, et al. Centrifugal Expansion of High-Speed Spindle and Its Influences on Bearing Dynamic Characteristics[J]. Journal of Mechanical Engineering, 2012,48(19): 59-64 (in Chinese)

[8]田久良,洪军,朱永生,等. 机床主轴-轴承系统热-力耦合模型及其动态性能研究[J]. 西安交通大学学报,2012, 46(7): 63-68

Tian Jiuliang, Hong Jun, Zhu Yongsheng, et al. Thermo-Mechanical Coupling Model and Dynamical Characteristics of Machining Spindle-Bearing System[J]. Journal of Xi′an Jiaotong University, 2012, 46(7): 63-68 (in Chinese)

[9]方兵,张雷,曲兴田,等. 角接触球轴承刚度理论计算与实验[J]. 吉林大学学报:工学版, 2012, 46(7):63-68

Fang Bing, Zhang Lei, Qu Xingtian, et al. Theoretical and Experimental Research of Stiffness of Angular Contact Ball Bearing[J]. Journal of Jiling University: Engineering and Technology Edition, 2012, 46(7): 63-68 (in Chinese)

[10] 袁幸,朱永生,洪军,等. 精密球轴承不可重复跳动影响主轴动特性的预测[J]. 吉林大学学报:工学版,2012, 42(2): 382-387

Yuan Xing, Zhu Yongsheng, Hong Jun, et al. Prediciton Model of Spindle Dynamic Characteristics Affected by Non-Repetitive Run-Out of Precision Ball Bearing and Its Application[J]. Journal of Jiling University: Engineering and Technology Edition, 2012, 42(2): 382-387 (in Chinese)

[11] 黄浩,张鹏顺. 航空发动机角接触球轴承刚度的一种实用分析方法[J]. 南京航空航天大学学报,2000,32(4): 422-427

Huang Hao, Zhang Pengshun. An Analytical Method of Stiffness for Angular Contact Ball Bearing of Aeroengine[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2000, 32(4): 422-427 (in Chinese)

[12] Yuan Kang, Huang Chihching. Stiffness Determination of Angular-Contact Ball Bearings by Using Neural Network[J]. Tribology International, 2006, 39: 461-469

[13] David Noel. Complete Analytical Expression of the Stiffness Matrix of Angular Contact Ball Bearings[J]. Journal of Tribology, 2013, 135(10):1-8

[14] Cao Yuzhong, Yusuf Altintas. A General Method for the Modeling of Spindle Bearing Systems[J]. Journal of Mechanical Design, 2004, 126: 1089-1104

[15] Guo Y, Parker R G. Stiffness Matrix Calculation of Rolling Element Bearings Using a Finite Element/Contact Mechanics Model[J]. Mechanism and Machine Theory, 2012, 51:32-45

[16] Hagiu G D, Gafitanu M D. Dynamic Characteristics of High Speed Angular Contact Ball Bearings[J]. Wear, 1997, 211(1): 22-29

[17] 哈姆罗克 B J, 道森 D. 滚动轴承润滑[M]. 北京:机械工业出版社,1988

Hamrock Bernard J, Dowson D. Rolling Bearing lubrication[M]. Beijing, China Machine Press, 1988 (in Chinese)

[18] Gupta P K, Cheng H S, Forster N H. Viscoelastic Effects in MIL-L-7808-Type Lubrication PartⅠ: Analytical Formulation[J]. Tribology Transactions, 1992, 35(2): 269-274

[19] Hamrock B J, Dowson D. Isothermal Elastohydrodynamic Lubrication of Point Contacts, Part Ⅲ Theoretical Formulation[J]. ASME Journal of Lubrication Technology, 1977, 98(2): 264-272

[20] Harris T A. 滚动轴承分析[M]. 北京:机械工业出版社,1997

Harris T A. Rolling Bearing Analysis[M]. Beijing, China Machine Press, 1977 (in Chinese)

Research on Stiffness Characteristics of High Speed Angular-Contact Ball Bearing Considering Elastohydrodynamic Lubrication Effect

Yu Yongjian1, Chen Guoding1, Li Jishun2

(1．Department of Mechanical Engineering，Northwestern Polytechnical University，Xi'an 710072，China 2．Henan Key Laboratory of Modern Mechanical Design and Transmission System，Luoyang 471003，China)

Abstract:The stiffness characteristics of high-speed angular contact ball bearing have important influence on the dynamic characteristics of an aero-engine′s rotor system. To obtain them under oil lubrication condition, the elastohydrodynamic lubrication (EHL) effect on the stiffness characteristics of the ball bearing needs to be considered. Based on Jones pseudo-static mechanical model, a ball bearing stiffness calculation model is established by coupling the contact stiffness between ball and ring and its oil film stiffness, taking into consideration the EHL effect. The ball bearing stiffness calculation model is used to study the influence of EHL effect on the ball bearing stiffness. The exploration results show that the ball bearing stiffness with the EHL effect considered is obviously lower than the ball bearing′s stiffness without considering the EHL effect. The ball bearing′s radial stiffness is more sensitive to the EHL effect than the ball bearing′s axial stiffness. With the EHL effect considered, the ball bearing stiffness decreases with increasing dynamic viscosity coefficient and pressure viscosity coefficient respectively. The ball bearing′s radial stiffness increases with its temperature viscosity coefficient, but temperature viscosity coefficient has no effect on its axial stiffness. The influence of the EHL effect on the ball bearing′s axial stiffness becomes more obvious when the rotor speed increases, but its influence on the ball bearing′s radial stiffness is waning. Its influence on the ball bearing stiffness does not change with the load variation.

Keywords:ball bearings, calculations, elastic deformation, elastohydrodynamic lubrication, film thickness, geometry, liquid films, pressure, stiffness, temperature, viscosity; bearing stiffness, contact stiffness, elastohydrodynamic lubrication effect, high-speed ball bearing, oil film stiffness

中图分类号：TH133

文献标志码：A

文章编号:1000-2758(2016)01-0125-07

作者简介：余永健(1979—)，西北工业大学博士研究生，主要从事滚动轴承性能分析及理论研究。

基金项目：国家自然科学基金(51375148)资助

收稿日期：2015-09-10