模糊控制辅助的GNSS/INS深耦合跟踪算法

何伟, 廉保旺, 张玲玲

(西北工业大学 电子信息学院, 陕西 西安　710072)



模糊控制辅助的GNSS/INS深耦合跟踪算法

何伟, 廉保旺, 张玲玲

(西北工业大学 电子信息学院, 陕西 西安710072)

摘要：深耦合跟踪环路在INS的辅助下可以有效提高GNSS接收机在高动态条件下的跟踪性能。但是如果INS模块发生故障，会导致GNSS跟踪环路的失锁或处于误跟踪状态，从而导致整个GNSS系统的发散。针对这种发散问题，在不降低系统动态性能的前提下，提出了一种模糊控制辅助的深耦合跟踪算法，该算法通过动态控制INS实现对GNSS深耦合跟踪的辅助，并建立了相应的切换准则。仿真分析结果表明，该深耦合跟踪算法在不降低GNSS跟踪环路动态性能的前提下，可以有效降低由于INS模块失效对GNSS跟踪环路的影响。同时由于GNSS接收机在INS单元故障的情况下依然可以正常工作，因此可有效地提高整个深耦合系统的鲁棒性。

关键词：模糊控制；组合导航；深耦合系统；鲁棒性

许多学者针对GNSS/INS组合导航系统展开了研究[1-3]。而组合导航系统中，数据融合是最关键的研究方向之一。在现有的数据融合算法中，Julier针对非线性系统的最优估计问题提出了UKF算法[4]，该算法相对于传统的EKF算法有效地提高了数据融合的精度，Chang Guobin提出了边缘UKF算法[5]，在不降低数据融合精度的前提下，该算法相对于传统的UKF算法降低了运算的复杂度以及UKF算法的实现难度。为了适应更加复杂的高动态外部环境，Babu等提出了多种INS辅助GNSS接收机跟踪环路的深耦合导航方法[6-7]，Dah-Jing Jwo等人在该类方法的基础上提出了基于模糊控制辅助无迹粒子滤波的深耦合跟踪算法(FUPF)[8]，该算法有效地提高了高动态条件下深耦合跟踪环路的定位、定速结果。Wang Jinling等则在传统深耦合跟踪环路的基础上设计了GNSS/INS/PL深耦合导航系统，该系统在传统的深耦合系统的基础上引入了伪卫星信号作为新的观测量以提高深耦合系统的抗干扰性能[9]。但上述的方法和技术主要关注于GNSS/INS组合导航的性能，而对INS传感器错误数据的影响是不予以考虑的。导致GNSS或者INS系统中发生错误时，整个系统定位准确性下降。在GNSS/INS深耦合系统环境下，由于2个独立的系统之前互相辅助，因此当INS单元出现故障时会影响GNSS接收机的跟踪环路，从而造成失锁或误跟踪。

为了避免深耦合导航系统中，单一系统出现故障而导致整个系统出现错误，通常需要采用相应的抗野值算法与自适应完好性监测算法对INS的故障进行监测。Abdelhadib Benoudjit针对抗野值算法展开了大量的研究，文献[10]根据Kalman滤波新息正交性采用一个活化函数加权于新息序列，实时改变活化函数的取值,使野值对滤波的影响最小化，而不必考虑野值的分布情况。文献[11]基于稳健滤波的M估计技术,在卡尔曼滤波的基础上引进由影响函数导出的加权因子，对滤波过程中的新息进行修正，能够有效地对野值进行抑制。以上的这些算法在位置、速度出现突变时，可以有效地对INS单元的完好性进行监测并对野值点进行抑制，但是对于INS来说，INS器件出现故障虽然是突发性的，但是由INS故障所引起的位置、速度误差则是渐变性的。因此当INS器件出现故障时，以上的抗野值算法难以完成对INS单元的完好性监测。

综上所述，文献[8-9]中所提出的深耦合跟踪环路虽然可以提高GNSS接收机的环路跟踪性能，但是由于引入了2种导航系统导致整个系统出现故障的概率也大大增强，同时现有的抗野值算法难以对INS造成的渐变式误差进行判决，因此需要一种方法能够在不降低性能的前提下对GNSS接收机与INS进行部分隔离以降低系统发散的概率。基于以上分析，本文提出一种新的GNSS/INS深耦合跟踪算法来控制INS辅助环路自适应切换控制，在不降低GNSS接收机跟踪环路性能的前提下，该方法相对于现有的深耦合算法能有效地实现了GNSS接收机与INS的有条件隔离，降低了整个深耦合系统发散的概率，提高了系统的性能。

1GNSS/INS深耦合跟踪环路

针对传统的GNSS/INS深耦合系统[8](见图1)，GNSS接收机可以对INS系统进行数据传递对准并完成对INS传感器的校准。此外，INS单元结合星历数据可以实时计算出载体相对于卫星的多普勒频移的估计值，该估计值可应用于GNSS接收机的跟踪环路以提高GNSS接收机跟踪环路的动态性与灵敏度。

但是对于深耦合系统，INS与GNSS之间相互辅助会带来性能的提高以外，还会导致系统面临整体发散的风险。例如，当INS出现故障时会导致GNSS跟踪环路的失锁或误跟踪，而GNSS跟踪环路的失锁与误跟踪会影响对INS的传递对准，导致整个系统的发散。由以上分析可以看到GNSS/INS深耦合系统虽然可以提高2个系统各自的性能，但是深耦合系统会造成系统故障概率的增加。同时在外部环境较好以及载体动态性较低时，INS对GNSS跟踪环路辅助性能的提高也不是十分明显，此时2个系统完全可以相互独立工作以降低整个导航系统出错的风险。针对上述问题，本文提出了一种模糊控制辅助的GNSS/INS深耦合跟踪算法，该算法动态的对深耦合跟踪环路的INS辅助状态以及GNSS接收机跟踪环路的环路带宽进行调整。在不降低深耦合系统跟踪性能的条件下，有效降低了由INS故障所造成的深耦合系统发散的概率，从而提高了系统的鲁棒性。

2模糊控制辅助的深耦合跟踪算法

为了消除INS故障对深耦合系统的影响，本文设计了相应的模糊控制下的鲁棒深耦合跟踪算法，该鲁棒深耦合跟踪算法的结构如图2所示。由于需要对INS的辅助状态进行切换，因此，在本文中锁相环选取三阶锁相环以避免INS辅助分离时，导致GNSS跟踪环路失锁。该算法由辅助判决器1、辅助判决器2以及模糊控制器三部分构成，其中辅助判决器1和辅助判决器2分别在INS辅助分离或辅助状态下工作来决定深耦合跟踪环路的工作状态，模糊控制器在INS辅助分离式工作对三阶锁相环的带宽进行控制从而提高INS辅助分离式环路的跟踪性能。

该模糊控制下的鲁棒深耦合跟踪算法的流程如图3所示。

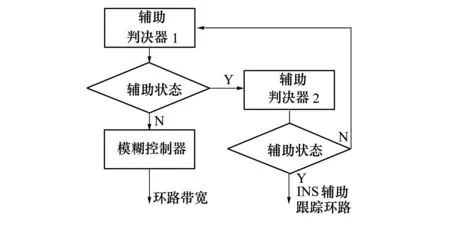
图3　算法流程图

在INS辅助分离状态下，系统进入辅助判决器1进行辅助状态判决，若辅助状态判决为辅助分离(N)， 则保持INS辅助分离的状态并进入模糊控制器来控制环路带宽。若辅助状态判决为辅助(Y)，则由INS辅助分离状态转为INS辅助状态并切换至辅助判决器2。辅助判决器2对辅助状态进行判决，若辅助状态为辅助(Y)，则继续维持INS辅助的状态，否则转入INS辅助分离的状态并切换至辅助判决器1。

2.1辅助判决器1

为了避免INS故障对GNSS接收机跟踪环路的影响，在GNSS接收机与INS辅助单元断开时，应避免使用INS辅助单元所提供的参数来确定深耦合跟踪环路的INS辅助状态。因此选取鉴相误差Δθ作为判决控制量以避免INS故障所造成的误判决。控制规则如表1所示，当开关控制的结果为0时，继续保持GNSS接收基于INS的深耦合分离状态，当开关控制量为1时，则跟踪环路由深耦合分离状态转换为INS辅助下的深耦合跟踪环路。

表1　辅助判决控制表1

2.2辅助判决器2

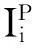
(1)

(2)

(3)

利用计算得到的载噪比与加加速度信息来对INS对深耦合跟踪环路辅助进行控制，需要建立相应的判决控制表。由(4)式可以得到在跟踪环路在不同的动态条件、载噪比以及环路带宽下的环路跟踪相位误差σ，从而得到三阶环路在不同载噪比与加加速度的条件下的最优环路带宽BL[12]，其计算公式如(5)式所示，从而得到在不同载噪比与加加速度条件下三阶锁相环的最优环路跟踪相位误差θL。

(4)

(5)

辅助判决器2的控制边界需要分别对最优化的环路跟踪带宽以及最优化的环路跟踪相位误差进行约束，约束式如(6)式、(7)式所示，由2个约束式可以得到辅助判决控制器2的边界，修正后可得到辅助判决控制表如表2所示。

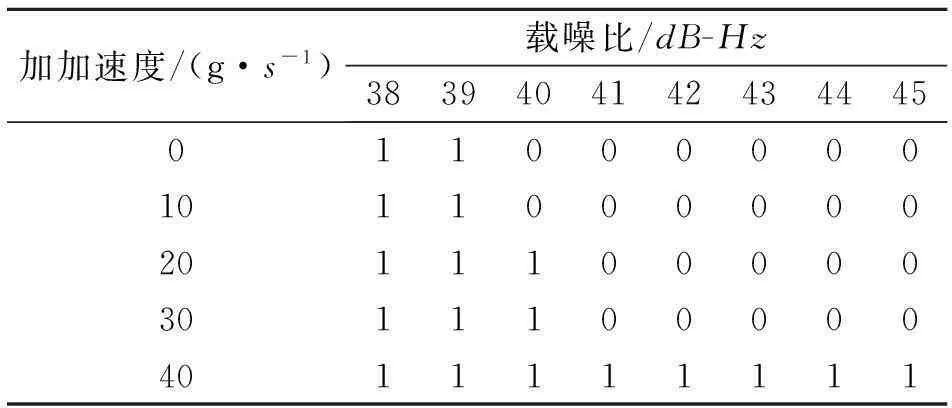
表2　辅助判决控制表2

(6)

(7)

当加速度较大时，耦合状态从INS辅助状态转换为INS不辅助状态时会造成环路的抖动。为了避免这种情况所引起的环路辅助反复切换的问题，本文对加速度进行约束。图4是在不同加速度的情况下由INS辅助转为INS不辅助的前100ms的时间内GNSS跟踪环路的相位跟踪误差的标准差，由该图可以看到，在加加速度为0时，由INS辅助状态转入INS辅助断开状态时，由于三阶锁相环需要一定的稳定时间，在最初的100ms的时间里跟踪环路的相位跟踪误差随着加速度的增加而增大。若状态切换过程中环路的抖动超过了辅助判决器1的门限则跟踪环路会立刻由分离状态转入深耦合辅助状态。在这种情况下，系统会出现反复切换深耦合跟踪环路的工作状态。

为了防止深耦合跟踪环路工作状态的频繁切换，以提高整个改进的深耦合跟踪算法的稳定性。本文引入了加速度约束条件作为对辅助判决器2的辅助。结合辅助判决器1的设计得到该加速度约束条件如下式所示，当(8)式不成立时，则保持深耦合跟踪环路处于辅助状态。

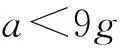
(8)

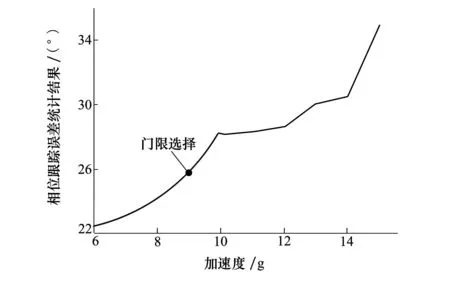
图4　不同加速度条件下切换造成的环路抖动

2.3模糊控制器的设计

为了保证在INS辅助分离的条件下，GNSS接收机的环路跟踪精度可以优于INS辅助下的环路跟踪精度，本文设计了相应的模糊控制器以获得最佳的环路跟踪带宽。

模糊输入量为：载噪比C/N0，环路跟踪相位误差Δθ

模糊输出量为：环路带宽BL

载噪比C/N0的论域为非常小(PSS)，很小(PS)，稍小(MS)，中(M)，稍大(MB)，很大(B)，隶属度函数采用三角形函数如图5所示。

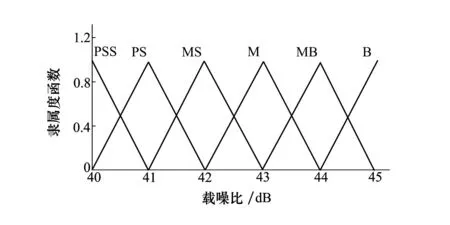
图5　载噪比的隶属度函数

环路跟踪相位误差Δθ的论域为零(Z)、小(S)、中(M)、稍大(MB)、大(B)，隶属度函数采用三角形函数如图6所示。

图6　相位跟踪误差的隶属度函数

环路带宽BL的论域为很小(PSS)、小(PS)、稍小(PMS)、中(PM)、稍大(PMB)、大(PB)、很大(PBB)，隶属度函数采用三角形函数如图7所示。

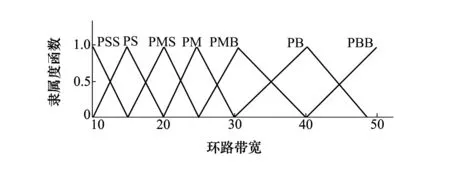
图7　环路带宽的隶属度函数

模糊控制规则表如表3所示。

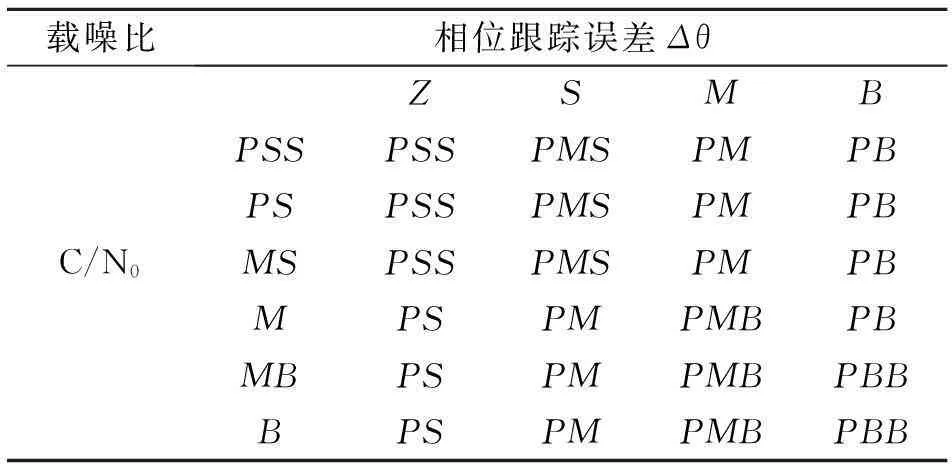
表3　模糊控制规则表

模糊控制规则共24条，关系词采用if-and-then，例如

IfΔθisZandC/N0isPSSthenBLisPSS

其中模糊推理方法采用Mamdani极大极小推理法，模糊判决采用重心法。以上是整个模糊控制器的设计方法。

3跟踪环路切换规则

在深耦合跟踪条件下，INS实时辅助着GNSS接收机的载波跟踪环路，INS单元完成了对载波频率的跟踪，此时GNSS接收机的跟踪环路可以等效为静止状态下的载波跟踪环路，因此载波跟踪环路中不会保留跟踪过程中的载波频偏。此时如果直接取消INS单元对GNSS跟踪环路的辅助，则会造成载波频偏的急剧增大，进而导致跟踪环路的发散。为了验证以上的分析，做如下的仿真。

在2 g动态，载噪比为44dB-Hz的条件下，分别针对条件1)、在INS单元辅助；条件2)、INS单元不辅助；条件3)、INS单元辅助但在第3s断开3种情况进行仿真，载波频率跟踪误差的仿真结果如图8所示，由仿真图可以看到，在2 g的动态条件下，INS辅助下的深耦合跟踪环路以及INS不辅助的三阶锁相环路均可以正确地对载波频率进行跟踪。由图8可以看到，INS辅助单元直接断开的情况下，载波跟踪环路无法正常对载波频率进行跟踪，跟踪环路发散，系统进入误跟踪状态，严重的影响了系统的性能。

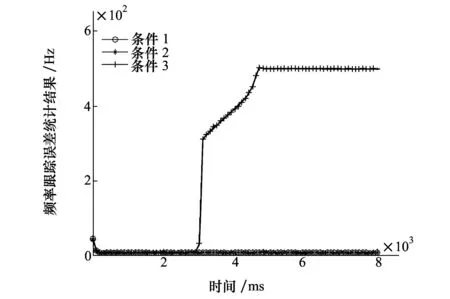
图8　3种条件下的频率跟踪误差

因此对于深耦合系统来说，不能简单地接通或断开INS对GNSS接收机载波跟踪环路的辅助，必须设计一套相应的断开接通方法以及相应的环路切换单元，以保证深耦合系统在切换跟踪状态是仍然可以正常工作，不影响系统的整体性能，同时避免误跟踪情况的发生。

设计的环路切换单元如图9所示，由INS获得的载波频率估计量fINS与切换频率fSwitch相减，频率累加锁存量fCal相加即可得到载波跟踪环路辅助量fAid，具体运算如(9)式所示，其中KSwitch为INS辅助开关量，当INS单元辅助GNSS接收机载波跟踪环路时KSwitch为1，不辅助时为0。

(9)

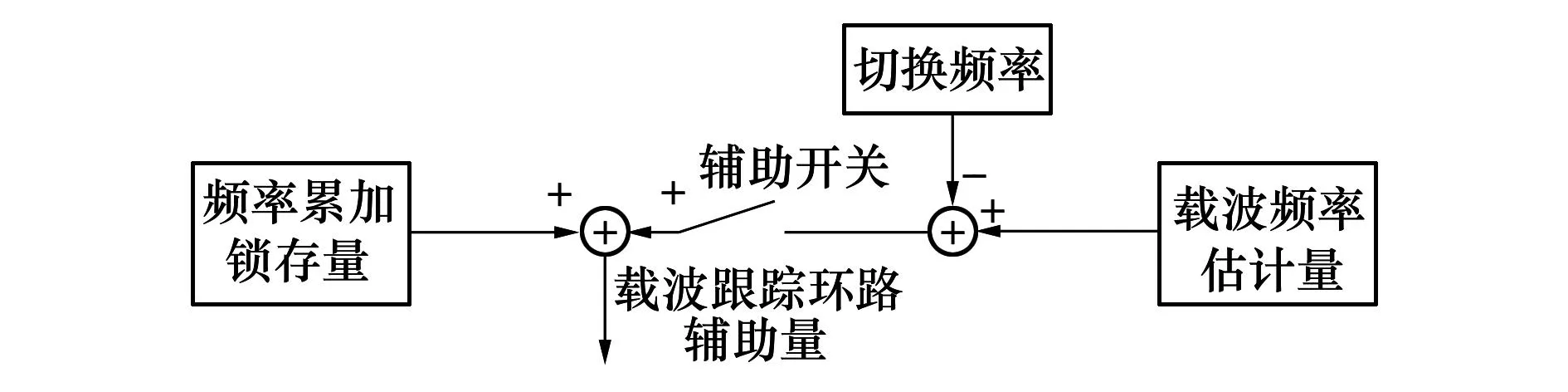
图9　环路切换单元原理图

INS辅助状态切换时应对切换频率fSwitch、频率累加锁存量fCal以及INS辅助开关量KSwitch进行更新，具体更新准则如下：

1) 由断开改为连通

当模糊控制器1给出连通信号时，此时INS单元对深耦合跟踪环路的辅助状态应由断开改为连通，此时，INS单元开始对GNSS接收机的载波跟踪环路进行辅助，因此，需要更新切换频率fSwitch与INS辅助开关量KSwich，具体的更新结果如(10)式、(11)式所示，其中fC-Loop为载波跟踪环路得到的当前的载波频率。

(10)

(11)

2) 由连通改为断开

当模糊控制器2给出断开信号时，此时INS单元对深耦合跟踪环路的辅助状态应由连通改为断开(INS单元并未对GNSS接收机的载波跟踪环路进行辅助)，此时应更新频率累加锁存量fCal以及INS辅助开关量KSwitch，具体更新结果如(12)式、(13)式所示

(12)

(13)

在引入该切换单元之后，为了比较性能，在第3节条件3)下再次进行仿真，得到载波频率的跟踪结果如图10所示。从图10可以看出，在引入了该环路切换单元后，可以实现深耦合系统跟踪环路的实时切换，增加了系统设计的灵活性，有效避免了INS辅助状态的切换对整个系统的影响。

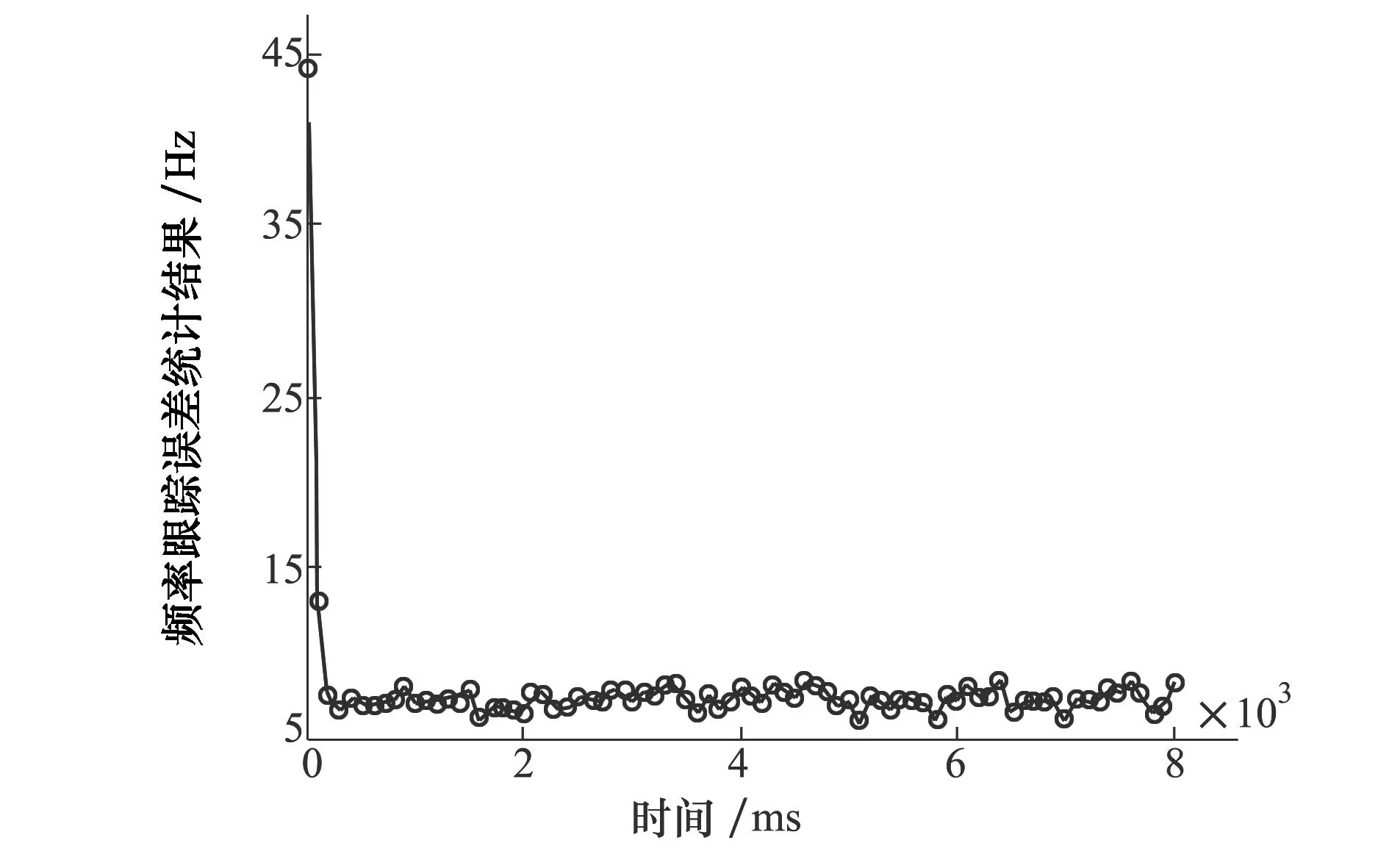
图10　切换单元控制下的深耦合跟踪环路频率跟踪误差

4仿真分析

为了对设计的基于模糊控制深耦合跟踪算法进行验证进行了仿真分析，设定了仿真条件和动态场景(见表4)如下：载体相对于卫星之间的初始速度为10m/s，模糊控制下的鲁棒深耦合跟踪算法每100ms进行一次判决操作并利用该跟踪判决的结果来调整跟踪环路的带宽。仿真分别对文献[7]提出的传统深耦合跟踪算法，文献[8]提出的基于模糊控制辅助无迹粒子滤波的深耦合跟踪算法以及本文提出的模糊控制辅助的深耦合跟踪算法进行了仿真，仿真结果如图11、12所示。

表4　仿真动态场景

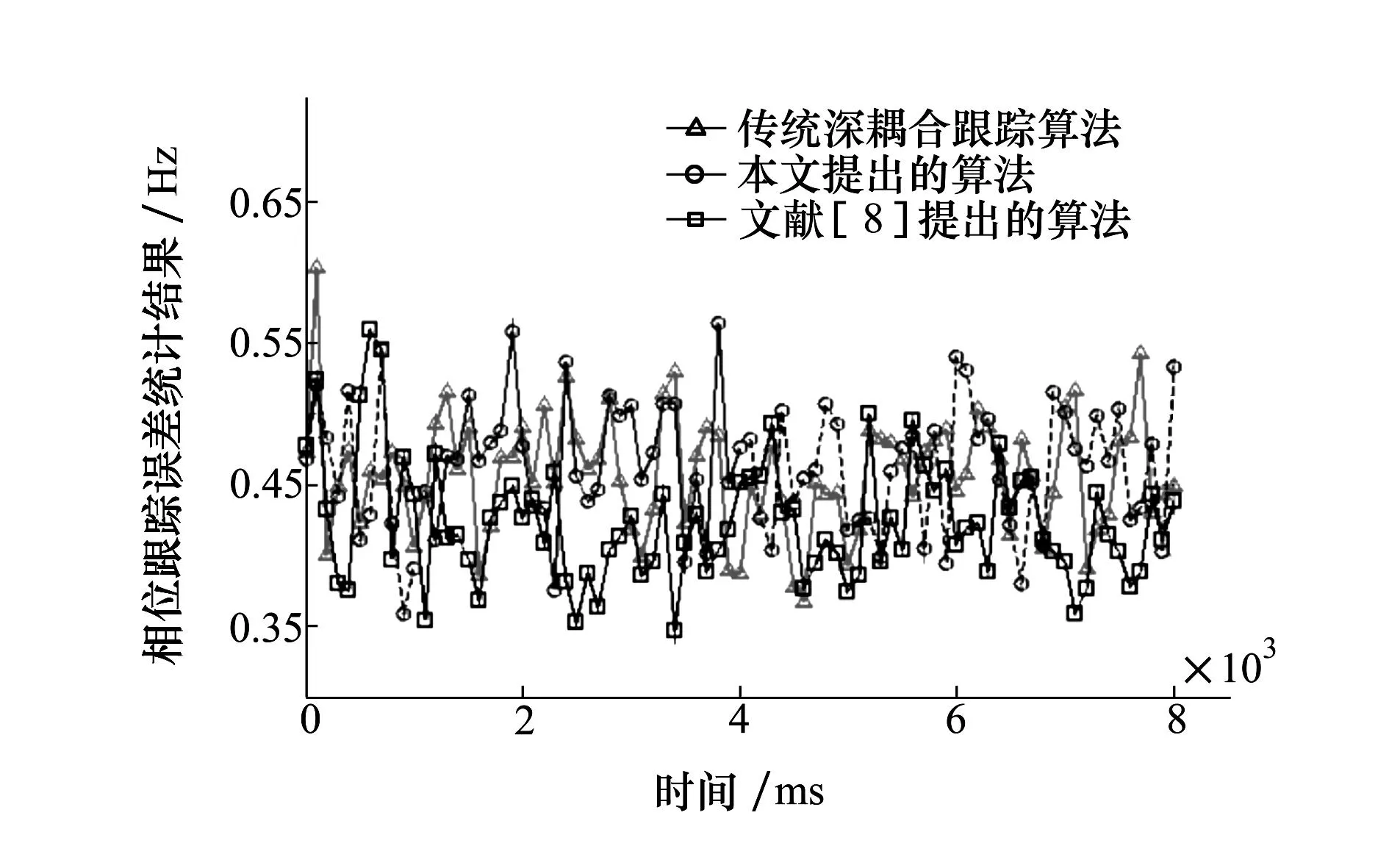
图11　相位跟踪精度对比

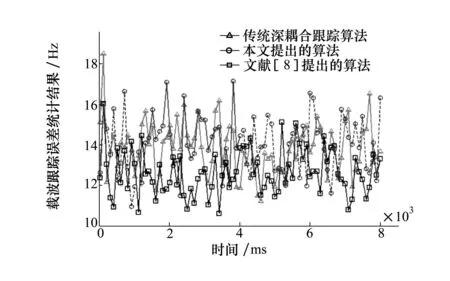
图12　频率跟踪精度对比

3种方法的环路相位跟踪误差与频率跟踪误差的对比如图11、12所示，其中实线代表INS的状态为辅助状态，虚线代表INS的辅助状态为分离状态。由仿真结果可以看到，模糊控制辅助的深耦合跟踪算法相对于其他2种深耦合跟踪算法来说相位跟踪精度与频率跟踪精度基本持平。由图11、12可以看到，在低动态条件下并且载噪比状况较好时，在模糊控制辅助的深耦合跟踪算法的控制下INS对于跟踪环路的辅助处于分离状态，此时INS若出现故障则不会对GNSS接收机造成影响，同时GNSS接收机还可以对INS进行传递对准，用于消除传感器故障对于定位解算结果的偏差影响。该算法从物理上将INS模块和GNSS接收机进行隔离，有效避免了由于INS故障而造成整个系统发散的风险。

为了对比模糊控制辅助的深耦合跟踪算法的系统性能，在上述仿真场景的第4.5～5.0s加入加速度扰动，即假设加速度计出现故障，加速度扰动的计算速度结果最大具有20 g的误差。3种深耦合跟踪算法的频率跟踪精度对比结果如图13所示。

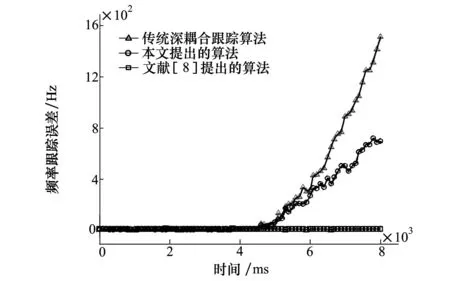
图13　器件故障条件下的频率跟踪精度对比

由仿真结果可得，本文所提出的深耦合跟踪算法在4.5～5.0s时，由于环路辅助状态为分离状态，所以加速度误差不会对GNSS接收机跟踪环路造成影响，整个环路保持稳定跟踪的状态。而其他2种深耦合跟踪算法在第4.5～5.0s之间载波频率无法锁定，处于发散状态。同时由于在4.5～5.0s之间环路无法正确的对INS单元进行对准，会导致在5.0s之后即器件故障消失后载波频率仍然处于发散的状态，跟踪环路无法对载波频率进行持续的跟踪。此外，基于模糊控制辅助无迹粒子滤波的深耦合跟踪算法由于数据融合精度较高，可以得到更高精度的多普勒频移估计量来辅助GNSS接收机跟踪环路，因此其载波频率偏移相对于传统的深耦合跟踪算法也较小。

5结论

本文提出了一种模糊控制辅助的GNSS/INS深耦合跟踪算法。该算法结合现有的接收机设计方法设计了相应的辅助判决器来控制INS对于GNSS接收机环路的辅助，并提出了相应的辅助切换方法。为了不降低整个深耦合跟踪环路的性能，该深耦合跟踪算法在GNSS接收机跟踪环路的INS辅助状态为分离时，通过本文所提出的模糊控制算法对环路带宽进行调整以保证深耦合跟踪环路的性能。仿真分析结果表明，在低动态条件下本文所提出的方法相对于现有的深耦合跟踪方法可以有效避免由于器件故障所造成的跟踪环路发散，并且在深耦合条件下能保证GNSS接收机的跟踪精度。在高动态环境下，该方法可以有效提高GNSS接收机系统的抗干扰能力。

参考文献：

[1]MuradyanPaytsar,HaaseJenniferS,XieFeiqinetal.GPS/INSNavigationPrecisionandItsEffectonAirborneRadioOccultationRetrievalAccuracy[J].GPSSolutions, 2011, 15(7): 207-218

[2]NoureldinA,KaramatTB,EbertsMD,etal.PerformanceEnhancementofMEMS-BasedINS/GPSIntegrationforLow-CostNavigationApplications[J].IEEETransonVehicularTechnology, 2009, 58(3): 1077-1096

[3]唐成凯，廉保旺，张玲玲. 卫星通信系统双向中继转发自干扰消除算法[J]. 西安交通大学学报, 2015,49(2):74-79

TangChengkai,LianBaowang,ZhangLingling.AnAlgorithmtoEliminateSelf-InterferenceofBidirectionalRelayingforSatelliteCommunicationSystems[J].JournalofXi′anJiaotongUniversity, 2015, 49(2): 74-79 (inChinese)

[4]JulierS,UhlmannJ,Durrant-WhyteH.ANewMethodfortheNonlinearTransformationofMeansandCovariancesinAltersandEstimators[J].IEEETransonAutomaticControl, 2002,47(8): 477-482

[5]ChangGuobin.LooselyCoupledINS/GPSIntegrationwithConstantLeverArmUsingMarginalUnscentedKalmanFilter[J].TheJournalofNavigation, 2014, 67(1): 419-436

[6]BabuR,WangJ.ImprovingtheQualityofIMU-DerivedDopplerEstimatesforUltra-TightGPS/INSIntegration[C]∥GNSS2004,Rotterdam,TheNetherlands, 2004: 16-19

[7]BabuR,WangJ.AnalysisofINS-DerivedDopplerEffectsonCarrierTrackingLoop[J].TheJournalofNavigation, 2005, 58(3): 493-507

[8]JwoDahjing,YangChifan,ChuangCihhsun,etal.ANovelDesignfortheUltra-TightlyCoupledGPS/INSNavigationSystem[J].TheJournalofNavigation, 2012, 65(2): 717-747

[9]BabuRavindra,WangJinling.Ultra-TightGPS/INS/PLIntegration:aSystemConceptandPerformanceAnalysis[J].GPSSolutions, 2009, 13(1): 75-82

[10]BenoudjitAbdelhadib.ApplicationofGeneticAlgorithmwithaNovelAdaptiveSchemefortheIdentificationofInductionMachineParameters[J].IEEETransonEnergyConversion, 2005, 20(3): 284-291

[11]HauptrL.AdaptiveCrossedDipoleAntennasUsingaGeneticAlgorithm[J].IEEETransonAntennasandPropagation, 2004, 52(8): 1976-1982

[12]KaplanE.UnderstandingGPS:PrincipleandApplication[M]. 2ndEditionArtechHouse, 2006

GNSS/INS Ultra-Tightly Integrated Tracking Algorithm Assisted by Fuzzy Control

He Wei, Lian Baowang, Zhang Lingling

(Department of Electronics Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:Ultra-Tightly integrated tracking loop aided by INS can effectively improve the tracking performance of GNSS receivers under high dynamic conditions. However, in the event of INS faults, it will lead to loss of lock in the GNSS tracking loop or an error tracking statement, resulting in the divergence of the GNSS system. In view of the divergence problem, we present a high robustness GNSS/INS ultra-tightly integrated tracking algorithm based on Fuzzy Control. On the premise of not decreasing the dynamic performance of the system, we dynamically control the aid of the INS to the deeply coupled GNSS tracking loop, and establish the corresponding switching criteria. Simulation results show that the presented ultra-tightly integrated algorithm can effectively reduce the influence resulting from the faults of the INS module without decreasing the dynamic performance of the GNSS tracking loop. At the same time, as the GNSS receiver can still work properly in case of failure of the INS module, the robustness of the whole ultra-tightly integrated system has been improved effectively.

Keywords:acceleration, algorithms, calculations, calibration, computer simulation, controllers, data fusion, Doppler effect, efficiency, errors, estimation, flowcharting, fuzzy control, fuzzy rules, matrix algebra, membership functions, navigation, optimization, probability, robustness(control systems), sensors, signal receivers, switching frequency, target tracking, vectors, velocity; integrated navigation system, ultra-tightly integrated

中图分类号：TN967.2

文献标志码：A

文章编号:1000-2758(2016)01-0098-08

作者简介：何伟(1988—),西北工业大学博士研究生，主要从事卫星导航与组合导航系统研究。

基金项目：陕西省科技统筹创新工程重点实验室项目(2013SZS15-K01)资助

收稿日期：2015-09-29