基于遗传算法的半开环单侧副翼卡死控制

闫冰, 吴成富, 邵朋院, 程鹏飞

(西北工业大学 无人机特种技术重点实验室, 陕西 西安　710072)



基于遗传算法的半开环单侧副翼卡死控制

闫冰, 吴成富, 邵朋院, 程鹏飞

(西北工业大学 无人机特种技术重点实验室, 陕西 西安710072)

摘要：无人机副翼卡死会严重影响无人机的操纵性和安全性。针对单侧副翼极限位置卡死故障,提出了一种根据侧滑配平的半开环控制方法,该方法在不引入侧滑角反馈的情况下,通过侧滑角指令与洗出网络代替偏差量,利用副翼和方向舵产生一定的侧滑角来平衡滚转力矩。首先,分析了在不同侧滑下配平卡死故障的可能性,并提出了半开环控制方案; 然后,基于经典 PID结构研究了侧滑角指令生成和控制的方法;最后,为了改善半开环系统的性能,通过遗传算法对参数进行优化。仿真结果表明通过遗传寻优的半开环控制方案能使无人机在单副翼极限卡死时快速稳定,恢复操纵性能,该方案具有一定的可行性和合理性。

关键词：无人机;副翼极限卡死;半开环;侧滑角;洗出网络;遗传算法

无人机操纵面卡死故障会对其飞行安全性和操纵性产生不利的影响[1-3]。当故障发生时,通过容错控制,有可能使无人机从故障中恢复并安全返航,在减少损失的同时提高无人机的生存性[2]。

无人机在单副翼有限卡死时极易进入荷兰滚模态[1],当卡死角度较大时,不能利用剩余操纵面来进行补偿[1,4]。美国科林斯国际公司提出了使用迎角和侧滑角对故障飞机进行全姿态控制[2]的自适应容错控制方案,这种全姿态控制在试飞试验中取得了巨大的成功。佐治亚理工学院采用神经网络自适应容错控制的方法在双引擎飞机上进行了舵机卡死、机翼大面积损伤下的飞行试验[5]。以上文献中仅研究了零位附近有限位置的卡死,而实际遇到的操纵面卡死角度可能较大。文献[3]针对副翼极限卡死提出了一种基于侧滑配平的控制方法,但所需的外置侧滑角传感器价格昂贵,测量不准确且增加机载,不利于工程实现。

本文在文献[2-3]的基础上,针对某小型验证无人机,从侧滑角配平的思路出发,为利于试验应用,在不引入侧滑角反馈的情况下,研究了单副翼极限卡死(30°)的半开环控制方案。当无人机单侧副翼极限位置卡死时,自动产生侧滑角指令,通过洗出网络重构偏差量,产生滚转和偏航指令,提供额外的滚转力矩,以补偿副翼卡死带来的不对称力矩。为改善系统的动态性能,本文通过遗传算法[6]对参数进行寻优。仿真结果表明,在单侧副翼极限位置卡死故障下,不引入侧滑角反馈也能使无人机稳定姿态,恢复操纵。

1侧滑角配平的半开环控制方案

1.1单侧副翼卡死配平

当单侧副翼在极限位置卡死时,机体产生的气动力矩无法平衡卡死舵面产生的滚转力矩[1],飞机将失去操纵性。由文献[3]可知,若将左右副翼的舵效单独考虑,则整机的滚转力矩系数组成如下

(1)由(1)式可知,可以使用侧滑角β和左副翼同时进行配平,当右副翼在30°极限卡死时,随着配平中侧滑角的不断增加,各个舵面的变化曲线如图1所示。

侧滑角主要影响滚转力矩,在右副翼极限30°卡死时,随着侧滑角的增大,左副翼的配平值逐渐减

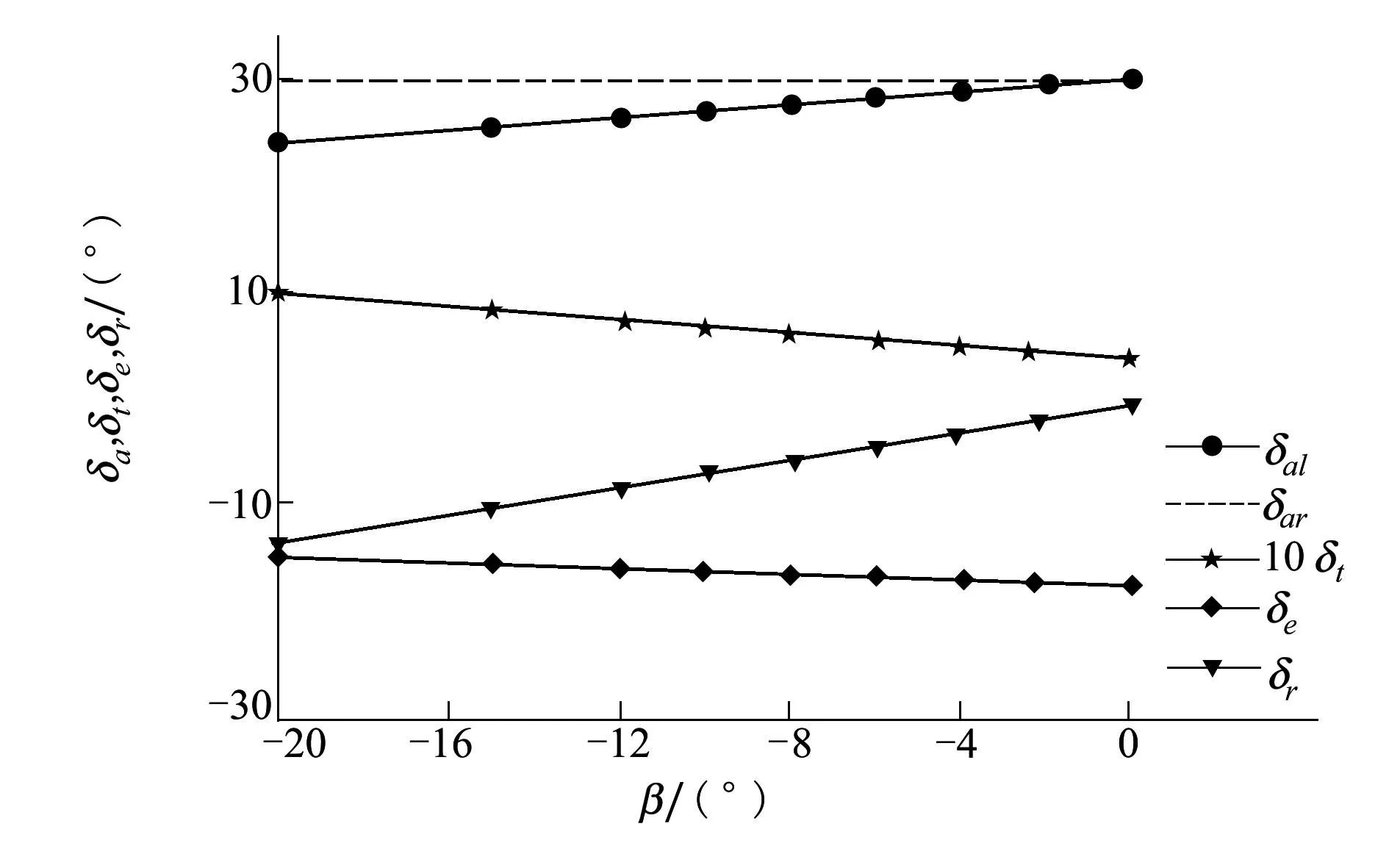
图1　不同侧滑下配平曲线

小,所激发出的剩余操纵量增大。但加入侧滑角会影响侧力,需要增大方向舵,用升力分量来平衡侧力,并且侧滑角会增加飞机的阻力,为了维持空速,需要消耗更多的动力,油门逐渐增加。由图1可知,在不同的侧滑角下,无人机都能达到一定的平衡,并且还有一定操纵余量。

1.2半开环控制方案

闭环控制方案是指通过副翼与最大操纵余量的偏差产生一定的侧滑角指令,引入侧滑角反馈并通过滚转和偏航指令稳定侧滑角,补偿滚转力矩[3],使副翼稳定到最大偏转量以下保持原有的操纵余量。闭环控制虽然可以快速使无人机稳定到给定的侧滑角上,系统性能良好,但由于侧滑角的测量需要外置传感器,无形中会增加机载,测量时受气流影响较大测量不准确,且价格昂贵。

本文从实际试验出发,在闭环控制的基础上,不引入侧滑角反馈,提出了半开环的控制方案,使用洗出网络代替反馈的偏差量,具体结构图如下:

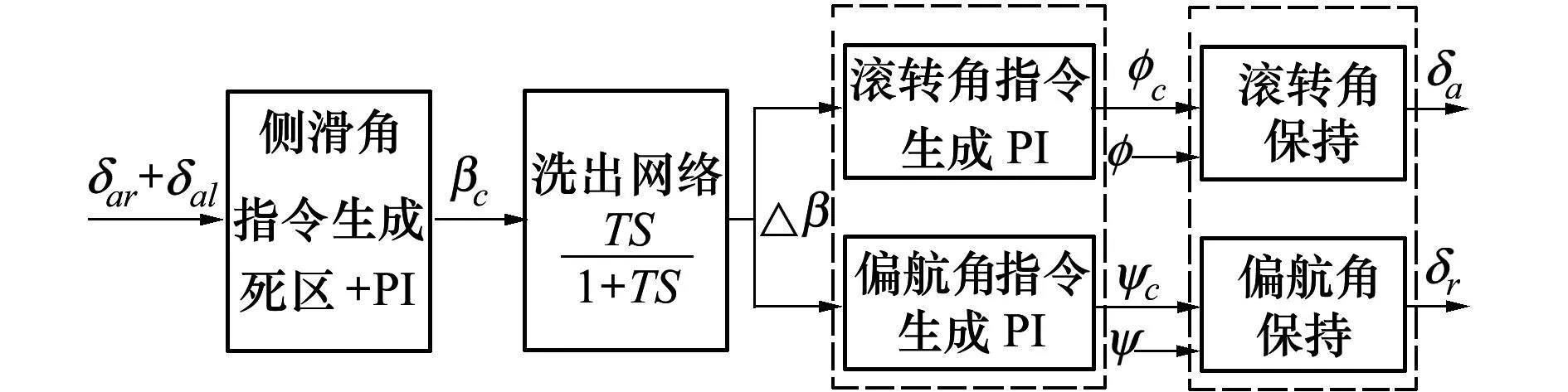
图2　半开环控制方案

半开环是指没有侧滑角反馈只有姿态角反馈,其中侧滑角指令通过死区环节和经典的PI结构自动生成,通过观测两副翼与给定门限之间的偏差判断是否卡死并自动生成侧滑角指令。洗出网络将侧滑角指令迅速衰竭到零,模拟反馈作用消除侧滑角误差。分别采用经典的PI结构产生滚转和偏航的指令,通过有反馈的姿态角保持,使无人机自动稳定到一个侧滑角上。这里的半开环控制是指横侧向的控制,纵向采用高度保持与自动油门控制。

使用洗出网络的半开环控制结构可以在卡死故障下稳定侧滑角的原因如下:

从洗出网络本身特性来看,洗出网络将输入信号迅速衰竭到零,这与侧滑角反馈的偏差信号的变化趋势一致,消除死区产生的信号,相当于最外环的反馈,进而使副翼稳定到死区门限内,达到保持操纵余量,稳定侧滑角的目的。

从控制结构上看,洗出网络与前面的PI控制器组合后为同阶次,相当于一个超前滞后控制器,再分别与后面滚转角偏航角指令生成中的PI相结合,本质上等效于图3的闭环控制结构,由最外环的死区特性的输出生成一定的滚转角和偏航角指令,经过姿态保持稳定一定的侧滑角,这里的偏航角保持也是为了稳定侧滑角,最终达到补偿滚转力矩,稳定另一个副翼的操纵余量的目的。

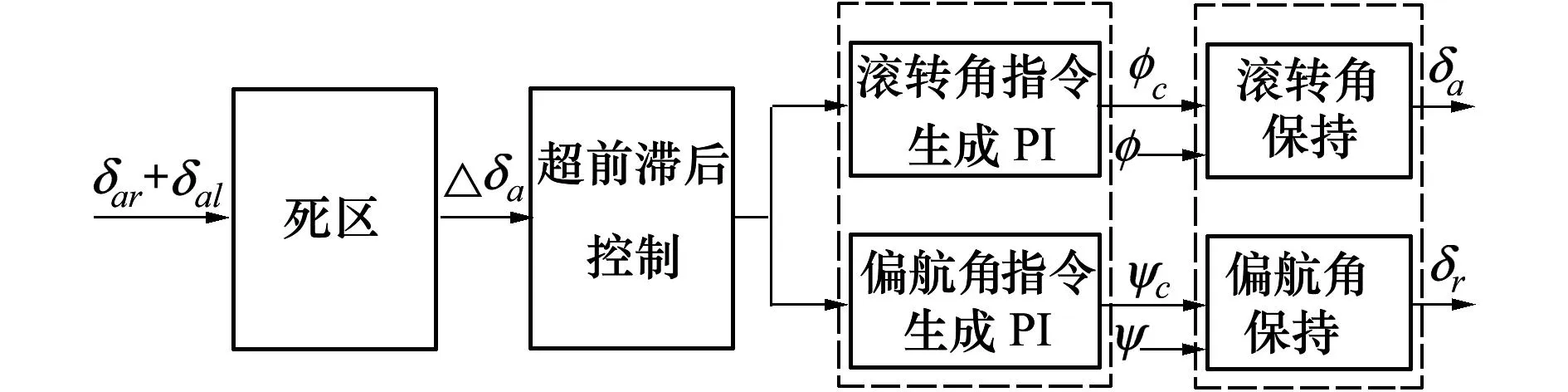
图3　半开环等效控制结构

由此可知半开环的控制方案可以在卡死故障下使无人机稳定在一个侧滑角上,运算简单,成本便宜,但加入洗出网络会造成一定的延迟,需要对系统的动态性能进行改进。以下我们都采用图2最初的半开环控制结构进行讨论,针对侧滑角指令生产模块,我们采用遗传PID算法进行参数全局优化,提高系统的动态性能。滑角指令生产模块如下:

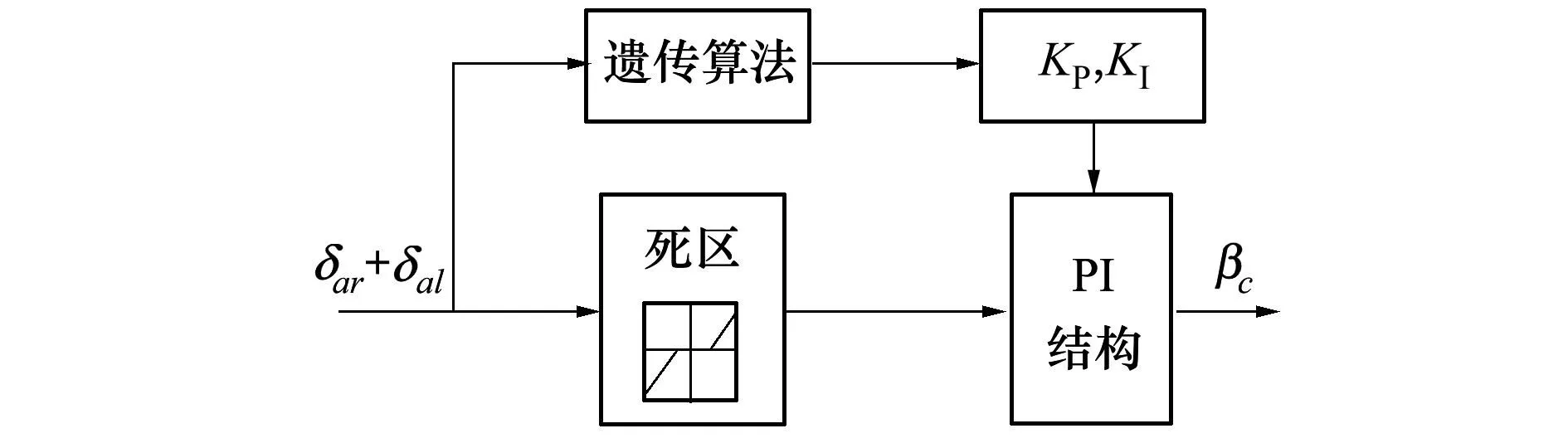
图4　侧滑角指令生成

2卡死控制器设计

2.1侧滑指令自动生成

本文涉及的无人机,副翼只做滚转使用,正常飞行状态下副翼差动,左右副翼之和在零附近。通过检测左右副翼之和可以判断卡死故障,根据两副翼的状态判断是否需要产生侧滑角来保证另一副翼的操纵余量,并自动生成相应的侧滑角指令。

首先通过检测两边副翼舵面的响应进行故障判断,若两边副翼之和在零附近很小的邻域内,则认为副翼正常工作,若在短时间内,左右副翼的和急剧增加,不再具有差动响应,则认为有副翼故障,当某一舵面响应不跟随时间变化时,则可以认为该副翼卡死,以下只考虑卡死故障。

当检测出一端副翼卡死时,需要根据飞行所需要的剩余操纵性来判断是否需要生成侧滑角指令,卡死位置较小时光靠自身的操纵面就可以配平,卡死位置较大时需要产生侧滑角指令,这里使用两舵面和的自适应侧滑角指令生成器。

(2)

(3)

(4)

侧滑角自动生成器主要由一个死区环节和PI结构组成。其中,δmax为副翼卡死的极限位置,本文中取30°,δlim为去除最小剩余操纵量的最大偏度,其取值跟高度有关,如在低空时可给定较大的δlim来生成较小的侧滑角指令,便于安全着陆,本文只考虑等高平飞状态,这里取定值20°,即用于稳定的两副翼和最大为50°,最小的操纵余量为10°。k为取符号结果,根据(|δal|-|δar|)的正负判断侧滑指令的正负,例如右副翼在极限位置+30°或-30°卡死时,(|δal|-|δar|)取符号后为-1,需要与Δδa反方向的侧滑来平衡滚转力矩,当左副翼±30°卡死时,需要与Δδa同方向的侧滑来平衡滚转力矩,|δal|-|δar|为正。这样的自适应指令生成器可以自动监测故障,并在超过操纵界限时产生相应的侧滑角指令。

侧滑角指令的生成采用经典的PI控制结构。比例项KP影响系统的响应速度和系统的调节精度,积分项KI用来消除误差,影响调节精度。对于这2个参数的优化,第3节有详细介绍。

2.2控制律设计

半开环的侧滑角控制分为3个部分,侧滑角偏差洗出网络,横侧向姿态角指令生成以及姿态保持。洗出网络结构如(5)式所示,其中T为时间常数,分解为单位一与惯性环节之差,在一定时间内,输入的信号将衰减到0,T越小衰减越快,这里取T=1。在侧滑指令生成器后面加入洗出网络,可以模仿反馈作用将输入的βc迅速衰减到零,其响应可以用来重构βc-β的偏差信号,这样虽不能准确跟踪指定侧滑角但可以稳定到某个侧滑角上,保持一定剩余操纵量。

(5)

(6)

当一侧副翼卡死时,通过副翼和方向舵的配合产生侧滑,横侧向姿态角指令生成器是指用经过洗出网络的Δβ产生滚转角和偏航角指令,这里采用PI的控制结构:

(7)

内环的姿态控制器使用经典的PID控制,滚转角保持和偏航角保持控制律如下:

(8)

在高度700 m,速度25 m/s平飞300 s时,将右副翼卡死在30°极限位置,分别使用半开环控制和有闭环控制的副翼变化如图5所示:

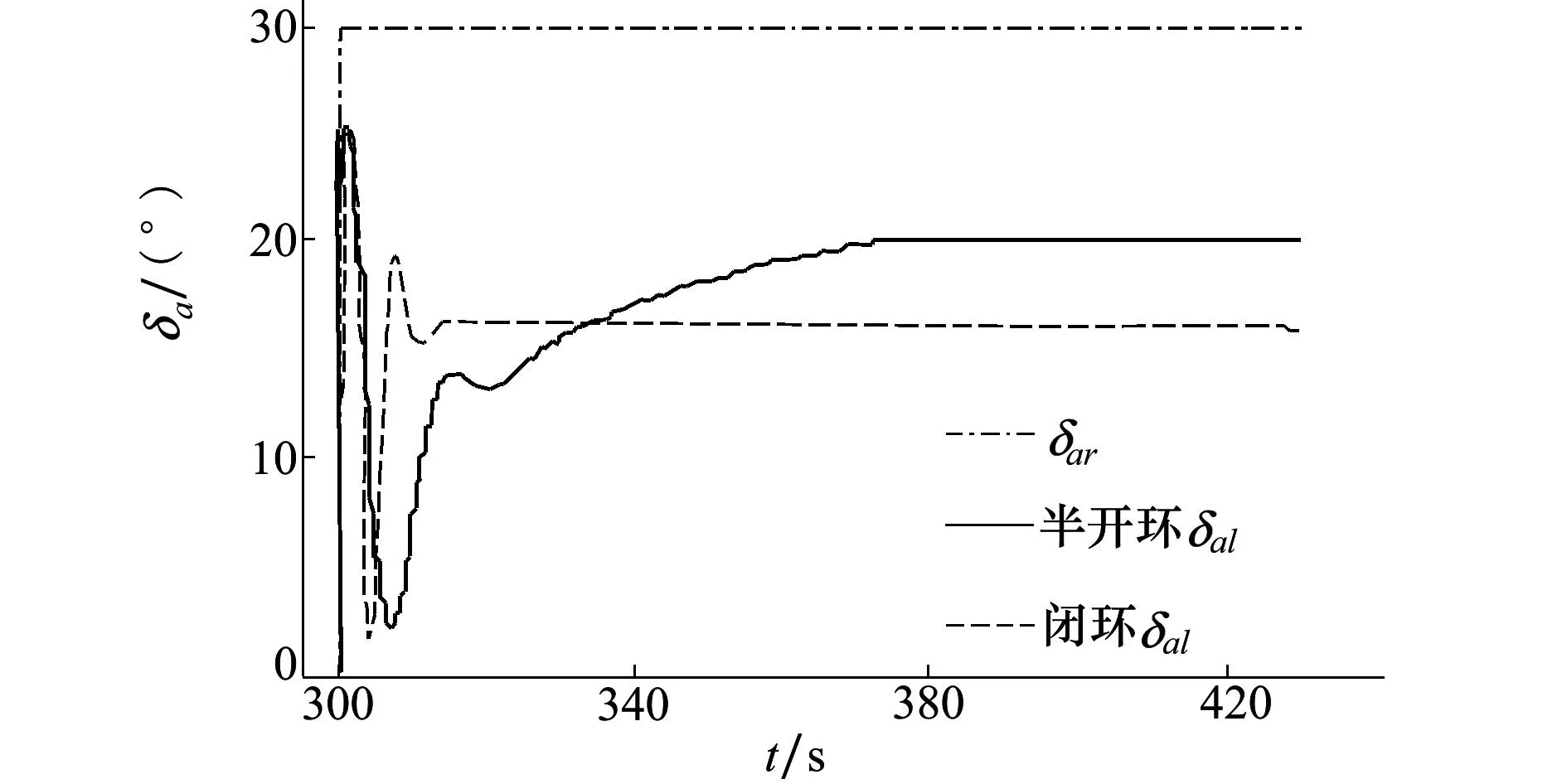
图5　侧滑角指令生成

左副翼在闭环控制下快速稳定到20°以下,性能恢复后剩余操纵量较大,正如之前分析,半开环的控制策略也可以使左副翼稳定在20°,恢复一定的操纵性能,但是较闭环系统相比调节时间较长,延迟较大,为了改善系统的动态性能,我们需要对半开环控制器参数进行优化。

3遗传算法参数优化

为改善半开环系统的性能,针对侧滑指令生成器(4)式中的PI控制参数进行遗传算法的寻优,首先,将参数(KP,KI)看作种群中的个体并初始化,计算每组参数下系统的目标函数,通过交叉和变异,不断筛选,直到找到最优个体,即控制器的最优参数。

3.1遗传算法实现

1) 编码与译码方式

遗传算法是从一个带有基因编码的种群开始的,而每个基因需要一定的编码。考虑到系统的寻优精度,这里采用10位无符号二进制数对参数KP、KI进行编码,每个基因长度为30,共同构成一条染色体,寻优结束后进行解码得到相应参数。

2) 初始化

根据预先估计的参数范围,等概率随机产生参数KP、KI的初始值。

3) 适应度函数与选择操作

适应度函数可以看作参数优化问题的代价函数,而选择操作就是选择最小代价进行遗传,对于如上系统,在调节过程中,首先要考虑卡死后达到稳定的快速性,这就需要加入调节时间的代价,其次还要考虑在调节过程中的震荡程度,这里用最大偏差和相对误差的代价来反应波动性。可将侧滑角指令生成器中死区的界限看作输入,两副翼舵值和看作输出,下面讨论右副翼在正极限位置+δmax卡死的情况,控制器使δal+δar在超过限定的剩余操纵量时向δmax+δlim靠近,这里的代价函数J为无量纲量,计算公式如下:

(9)

式中:第1项表示调节时间的代价值,ts为调节时间,Tl为总时间,用来反应系统的快速性;第2项为超调量的代价值,用来反应系统的最大偏差;第3项为相对误差的平方项,用来衡量系统整体的波动性。其中权值分别取λ1=0.4,λ2=0.3,λ3=0.3。

4) 交叉和变异

交叉是通过2个染色体基因的交换组合,产生新的优良品种,变异是对某些基因位作0和1的突变[6]。本文交叉概率和变异概率分别为:(其中Nsize为基因长度)

(10)

3.2算法流程图及结果

根据遗传算法的基本运算过程得到如下的算法流程图6。

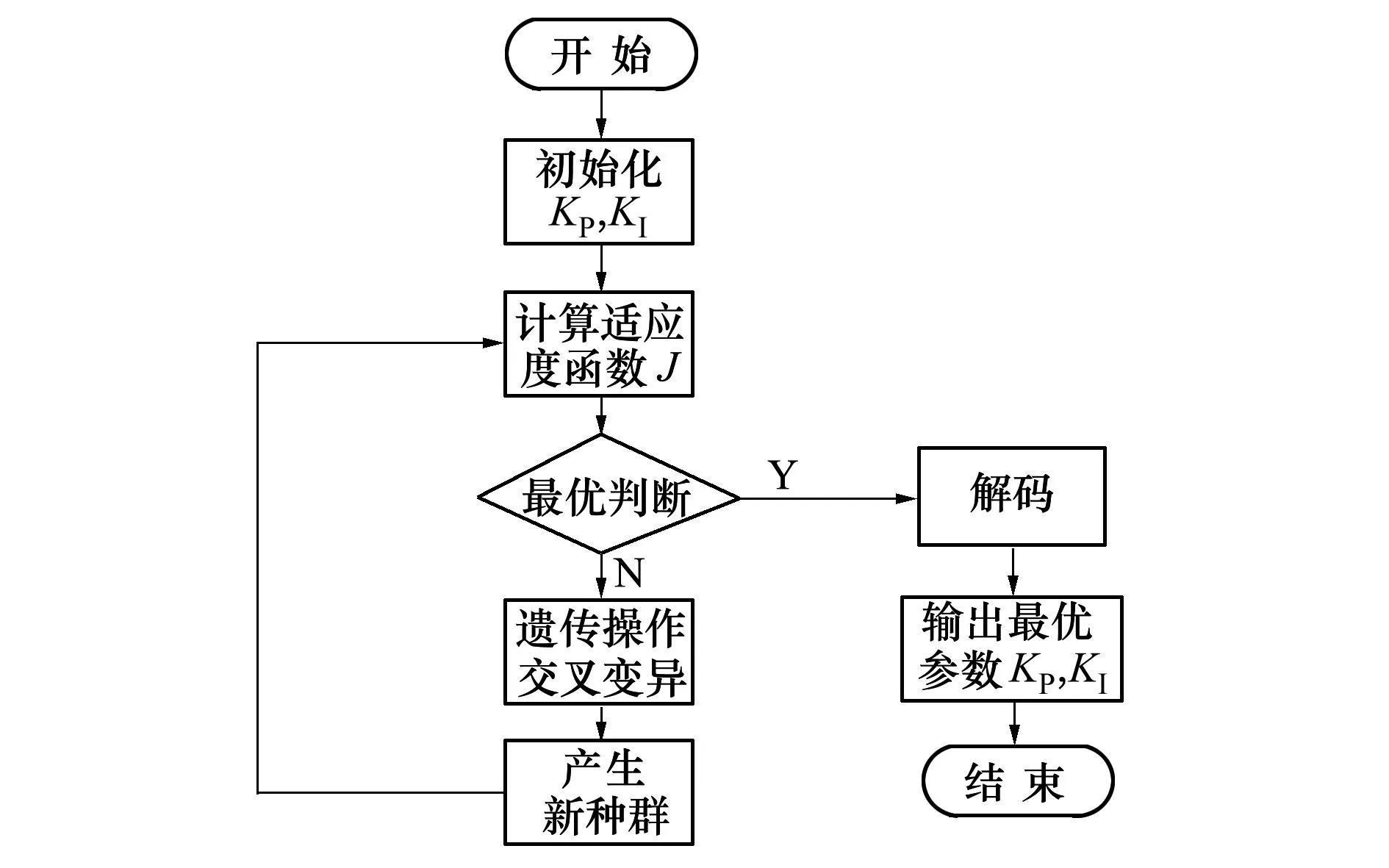
图6　遗传算法流程图

在右副翼30°卡死时,δmax+δlim为50°,在非线性系统中计算每组参数的适应度函数,对KP,KI2个参数在线寻优,得到KP=2.038 1,KI=1.910 1,其适应度函数及响应如图7所示:

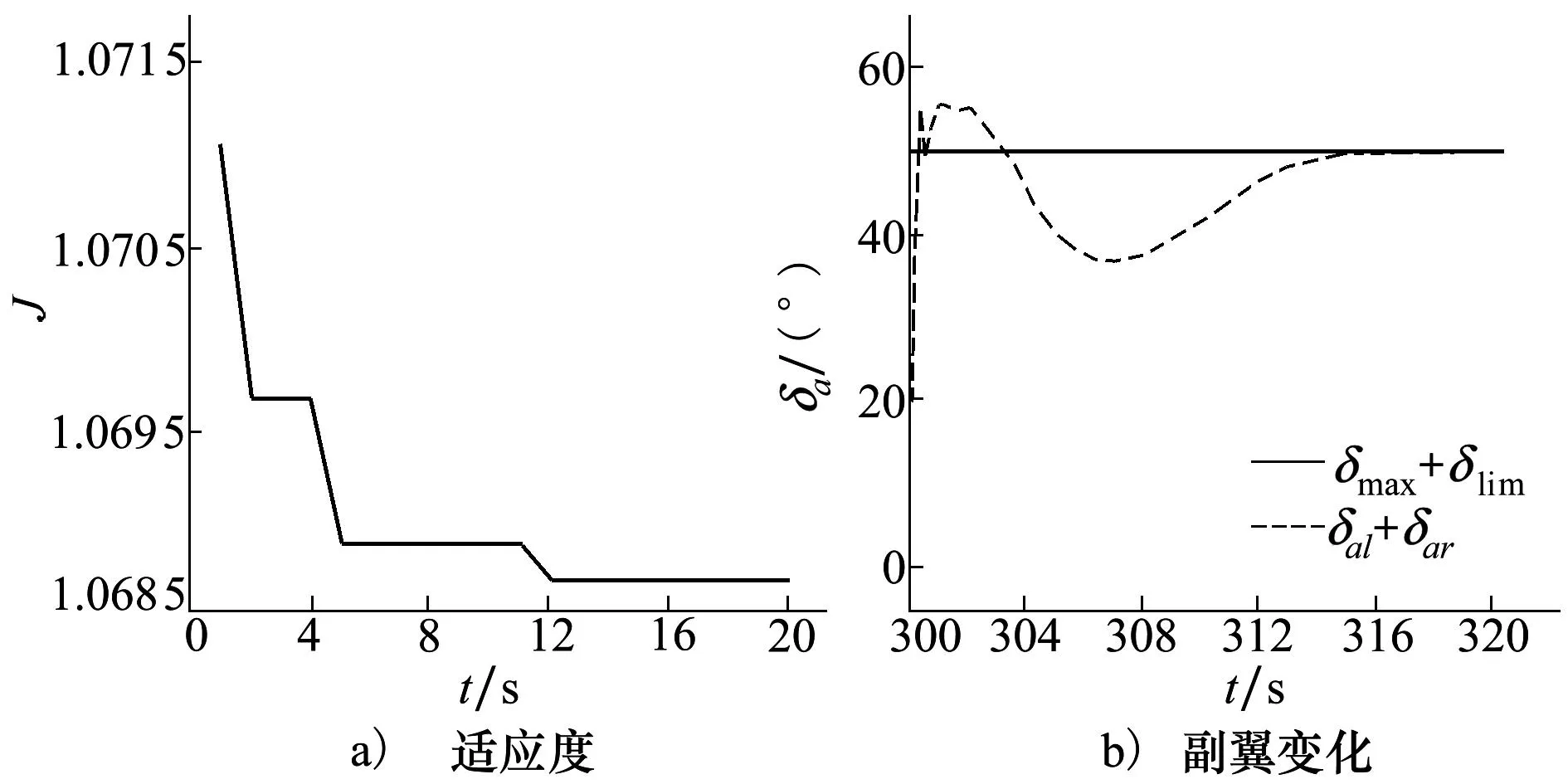
图7　适应度函数及副翼变化曲线

由图7可知,在算法寻优过程中,适应度函数一直在减小,响应的快速性和波动性的代价减小,系统的动态性能有所提高,与图5相比左副翼稳定到20°的时间从75 s下降到15 s,调节过程也更加平滑。

4仿真结果及分析

为了验证优化后半开环控制方案的可行性,需要在非线性模型中仿真，并定性比较半开环和闭环控制的结果。在700 m高度,25 m/s速度平飞300 s时,将右副翼卡死在30°极限位置,分别使用遗传算法寻优后的半开环控制方法和闭环控制方法进行仿真,其中相关量变化曲线如图8、图9所示。

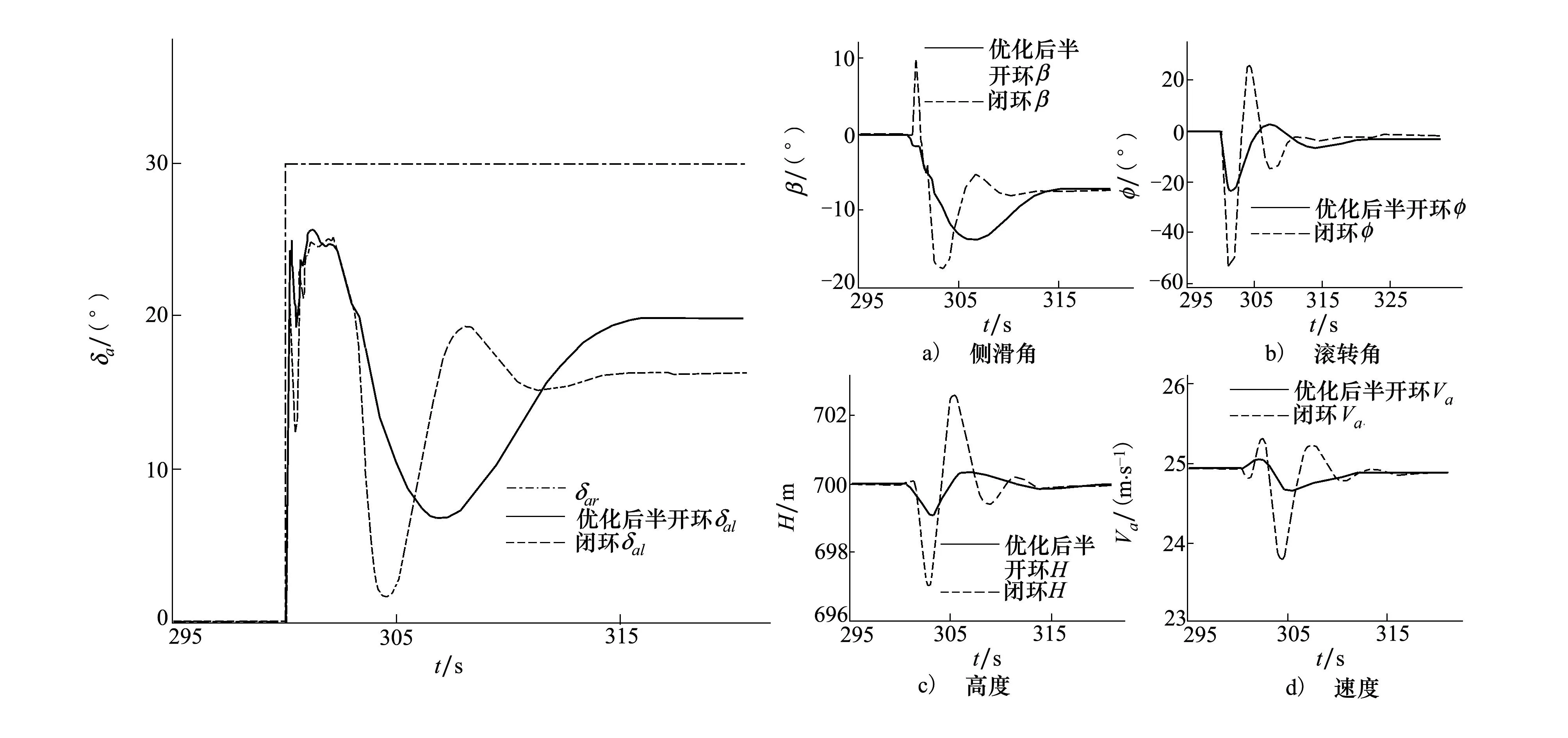
图8　优化后的半开环与闭环控制下的副翼曲线图9　优化后的半开环与闭环控制下的其他相关变化量

根据图8、图9对2种方案进行定性的对比,闭环控制经过12 s的时间就将侧滑角稳定下来,左副翼迅速稳定到20°以下,剩余操纵量较大,但调节过程中震荡较大,高度和速度在卡死调整过程中都有一定浮动的变化,稳定下来后基本与之前持平。在半开环控制器的作用下,15 s后左副翼稳定到20°左右,剩余操纵量为10°,调节过程较平缓,高度速度经过小幅震荡后恢复之前值。经过优化的半开环控制方案虽不如闭环响应迅速,但也具有一定的快速稳定性,计算简单且不需要昂贵的外置传感器。

5结论

本文针对单副翼极限卡死故障,分析了不同侧滑下卡死配平的可能性,提出了一种侧滑配平的半开环控制方法,半开环是指没有侧滑角反馈,通过侧滑角指令与洗出网络代替偏差量实现。详细介绍了半开环侧滑角指令生成及控制方法,为改善系统性能,提出一种遗传算法的 PID 参数优化策略。非线性仿真结果表明,无人机在单侧副翼极限位置卡死时,半开环的控制方案在不引入侧滑角反馈的情况下,能够快速稳定姿态,恢复一定的操纵性,在实际飞行试验中具有一定的可行性。

参考文献：

[1]王娜,席剑辉,黄宇,等. 无人机单副翼有限卡死时荷兰滚运动分析[J]. 仪器仪表学报,2009,30(6):838-842

Wang Na, Xi Jianhui, Huang Yu, et al. Analysis on Dutch Roll Modal of Unmanned Aerial Vehicle with the Limited Deadlocking of Single Aileron[J]. Chinese Journal of Scientific Instrument, 2009,30(6):838-842 (in Chinese)

[2]Damien B Jourdan, Michael D Piedmont, Vlad Gavrilets, et al. Enhancing UAV Survivability through Damage Tolerant Control[R]. AIAA-2010-7548

[3]吴成富, 邵朋院, 戢凤. 基于侧滑配平的单副翼极限位置卡死控制方法研究[J]. 西北工业大学学报, 2014, 32(1):137-141

Wu C F, Shao P Y, Ji F. An Effective Control Design for Single Aileron Jam at Ultimate Point via Trimming with Sideslip[J]. Journal of Northwestern Polytechnical University, 2014,32(1):137-141 (in Chinese)

[4]Barton J Bacon, Irene M Gregory. General Equations of Motion for a Damaged Asymmetric Aircraft[R]. AIAA-2007-6306

[5]Chowdhary G, Johnson E N, Chandramohan R, et al. Guidance and Control of Airplanes under Actuator Failures and Severe Structural Damage[J]. Journal of Guidance, Control, and Dynamics, 2013(4):1093-1104

[6]Matt Sorgenfrei, Sanjay S. Joshi, Amit K. Sanyal. On the Performance of a Genetic Algorithm for Spacecraft Controller Gain Optimization[R]. AIAA 2013-5029

A Method for Semi-Open Loop control of Single Aileron Jam Based on Genetic Algorithm

Yan Bing, Wu Chengfu, Shao Pengyuan, Cheng Pengfei

(State Key Laboratory of UAV Special Technology at Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:The aileron jam of an unmanned aerial vehicle (UAV) seriously affects its flight safety and maneuverability. This paper studies the UAV that has a single aileron jam at its extreme position and then proposes a semi-open loop control method based on sideslip trimming. Without introducing the feedback of a sideslip angle, the method uses the sideslip instruction and washout network instead of deviation in order to balance the rolling moment with the sideslip generated by the aileron and rudder of the UAV. The paper first studies different sideslips that may trim jam faults and proposes the semi-open loop control method. Then it presents the sideslip instruction generation and control method based on the classical PID structure. Finally, in order to enhance the performance of semi-open loop control system, it uses the genetic algorithm to optimize its parameters. The simulation results show that the semi-open loop control method based on the genetic algorithm can quickly stabilize the UAV and recover its operation performance when the single aileron jam occurs, indicating that the control method is feasible and reasonable.

Keywords:ailerons, attitude control, controllers, cost functions, genetic algorithms, safety engineering, unmanned aerial vehicles (UAV); semi-open loop control, sideslip angle, single aileron jam, washout network

中图分类号：V279

文献标志码：A

文章编号:1000-2758(2016)01-0079-06

作者简介：闫冰(1990—)，女，西北工业大学博士研究生，主要从事飞行控制与仿真技术研究。

收稿日期：2015-09-12