大扰动下Buck电源变换PCL控制器设计
2016-05-07许佳妮皇甫宜耿卓生荣庞圣钊
许佳妮, 皇甫宜耿, 卓生荣, 庞圣钊
(西北工业大学 ,陕西 西安 710072)
大扰动下Buck电源变换PCL控制器设计
许佳妮, 皇甫宜耿, 卓生荣, 庞圣钊
(西北工业大学 ,陕西 西安710072)
摘要:为提高系统在大扰动下的响应的快速性和鲁棒性,针对纯电动汽车上的DC-DC变换器,设计了一种基于prescribed convergence law(PCL)算法的鲁棒滑模控制器。以Buck变换器为例,验证该滑模算法在有限时间内的收敛性,并与PI和传统滑模控制效果进行对比。结果表明:①无扰动时,PCL滑模算法稳态精度高,调节时间短,输出纹波小;②输入电压和负载电阻大扰动时,PCL滑模算法响应速度更快,鲁棒性更强。
关键词:Buck变换器;滑模;PI;鲁棒性
随着石油枯竭、环境污染等问题的日益加剧,电动汽车成为近年来发展迅速的一种新型汽车, 其中纯电动汽车被认为是汽车工业的未来。而纯电动汽车行驶过程中,蓄电池组端电压和负载电阻的变化使电动机输入电压无法保持恒定,造成电动机驱动性能的恶化,所以有必要在蓄电池组与电动机之间加入DC-DC变换器,并对其控制。
经典的PID控制因其算法简单,适应性好,可靠性高而被广泛应用于工程实际中[1-2]。但其动态响应慢,控制效果差,无法满足电源变换器日益提高的动态响应和控制精度的要求。近年来,为改善变换器的控制性能,研究人员提出了很多先进的控制方法,如滑模控制、鲁棒控制[3-4]、双线性控制等[5]。其中滑模控制以其结构简单、对内部参数和外部扰动均不敏感的强鲁棒性得到了广泛应用[6]。然而传统滑模由于自身控制律的离散性存在抖振和控制精度问题,影响了滑模控制的效果。高阶滑模是传统滑模的推广,它既消除了传统滑模的缺陷,又保持了传统滑模优点。高阶滑模将不连续项放在滑模面的高阶导数中,实现了系统的平滑输出[7-9]。
本文采用高阶滑模中的prescribed convergence law(PCL)算法,并基于此算法设计了一种滑模控制器,将其应用于Buck变换器。然后从以下三方面对设计的变换器进行性能测试,并与典型PI和传统滑模控制效果对比:①无扰动时变换器稳态精度和调节时间;②大负载扰动下变换器的鲁棒性;③输入电压大扰动下变换器的鲁棒性。
1Buck变换器
1.1Buck变换器建模
Buck变换器是直流降压变换器,它是一种输出电压小于等于输入电压的单开关管非隔离型的直流电压变换器。
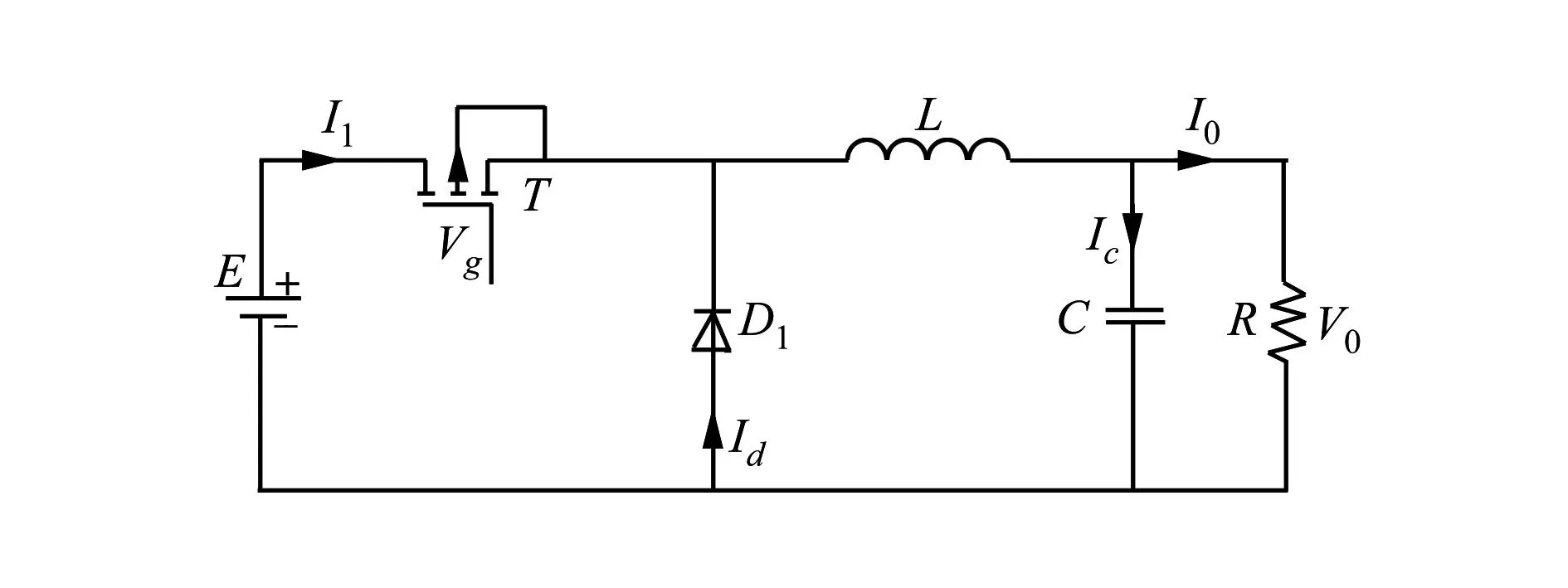
图1 Buck变换器拓扑结构
E为输入直流电压,T为开关管,Vg负责整个电路的通断,D1为续流二极管,L、C分别表示电感、电容,R为负载电阻,V0表示输出电压。
改变开关管T导通的占空比D达到降压的效果,可以推出一个周期Ts中输出电压的直流平均值
V0=D·E
(1)
假定负载为阻性负载,以电感电流iL与电容电压vc为状态变量,忽略电感和电容上的串联电阻,可得Buck变换器的状态空间方程[10]
(2)
1.2Buck变换器参数设计

表1 Buck变换器基本参数
电感L:
滤波电感的选择与负载电流的变化范围和期望的工作状态有关。假设电路工作在电感电流连续工作模式。当Buck变换器处于临界状态时,电感电流峰峰值2ΔiL与电感电流最小值Imin满足如下关系ΔiL=Imin。当开关管T导通时,即u=1,电感电流变化的斜率为
(3)
根据电感电流曲线斜率可得电感电流峰峰值
(4)
可得
(5)
计算可得L=6×10-6H,通常电路滤波电感取临界值的2~3倍,这里L取18×10-6H;
电容C:
滤波电容的值会影响电路输出电压,电流纹波和超调量的大小,通常,电容越小,超调越小,输出电压,电流纹波越大。
根据Buck变换器输出电压纹波要求计算如下
(6)
计算可得C=2.6×10-3F,C取3.0×10-3F。
2prescribed convergence law算法
高阶滑模实际上是在Filippov意义下,不连续动态系统的一种特殊类型的积分滑模面上的运动。高阶滑模将离散控制律转移至更高阶的滑模面,使滑模变量σ和直至σ的r阶导数均收敛于0。二阶滑模控制算法是最先出现的高阶滑模控制算法,prescribed convergence law算法是二阶滑模算法中的一种[11-12]。
设非线性控制系统
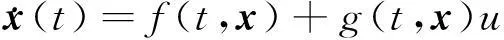

(7)
式中,x∈Rn,u∈R是控制律,σ是滑模变量。系统的控制目标是通过不连续反馈控制律使σ在有限时间内收敛于0
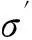
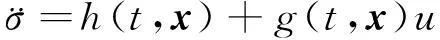
(8)
g和h满足不等式
(9)
上式对所有相对阶数为2的系统均满足。
prescribedconvergencelaw算法控制律定义如下[13]:
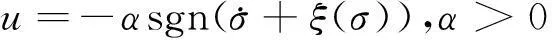
(10)
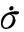
(11)
控制律变为
(12)
(12)式成立的前提条件
(13)
prescribedconvergencelaw算法收敛轨迹:
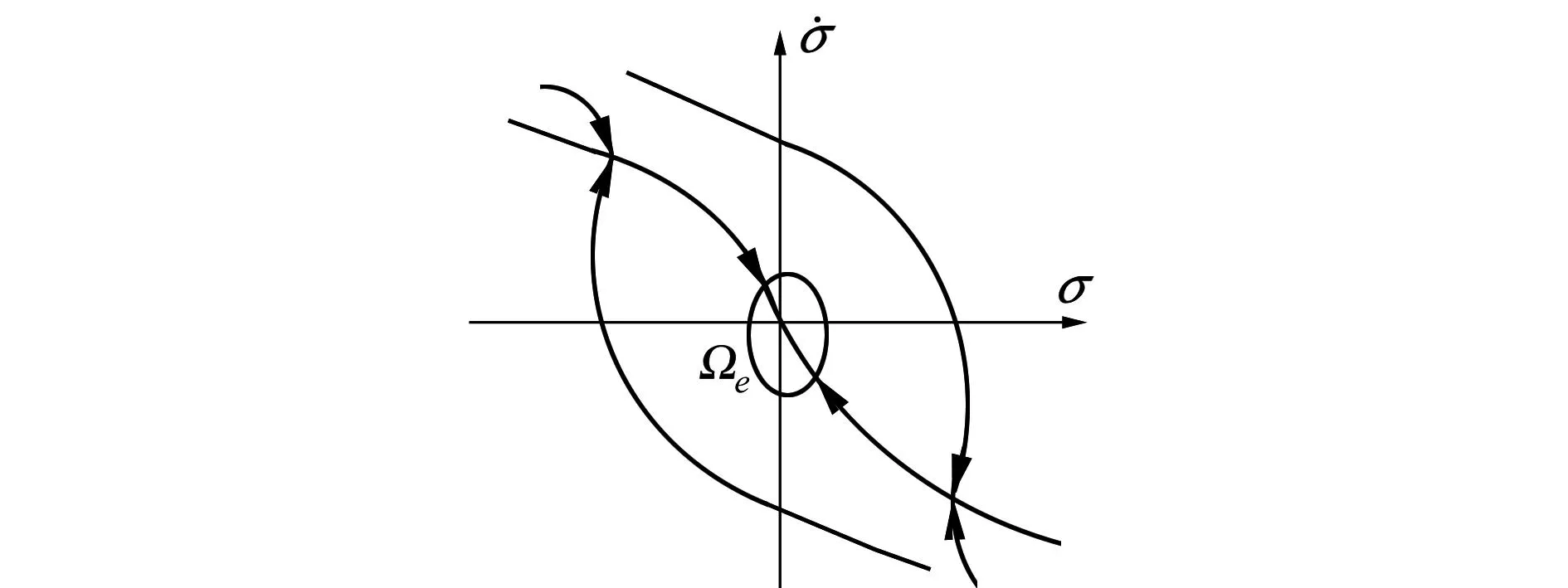
图2 PCL算法收敛轨迹
3控制器设计
对于Buck变换器,滑模变量σ=V0-Vref,σ的二阶微分表达式
(14)
将(2)式带入(14)式中可得
(15)
根据(8)式和(9)式可得
(16)
α=1时,(13)式可简化为
(17)
满足(17)式条件下,通过试验获得β值。β值越大,控制系统收敛速度越快。
4仿真结果对比分析
本文对基于prescribedconvergencelaw算法的Buck变换器在simulink中进行仿真,仿真中采用固定步长ode1,步长为1×10-6,经调试,α取1,β取1×104。
从图3可知,系统轨迹从某点出发,迅速到达滑模面,并进行滑模运动,最终稳定在(0,0)点附近振动。由此得出,系统实现了Buck变换器滑模变结构,验证了prescribedconvergencelaw控制的系统收敛性。
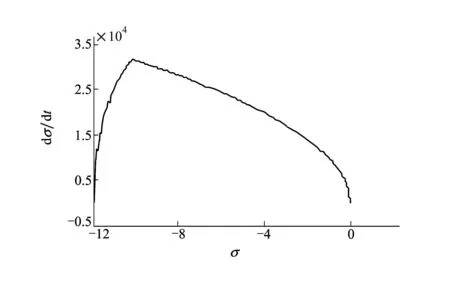
图3 PCL算法控制的变换器滑模变量收敛轨迹
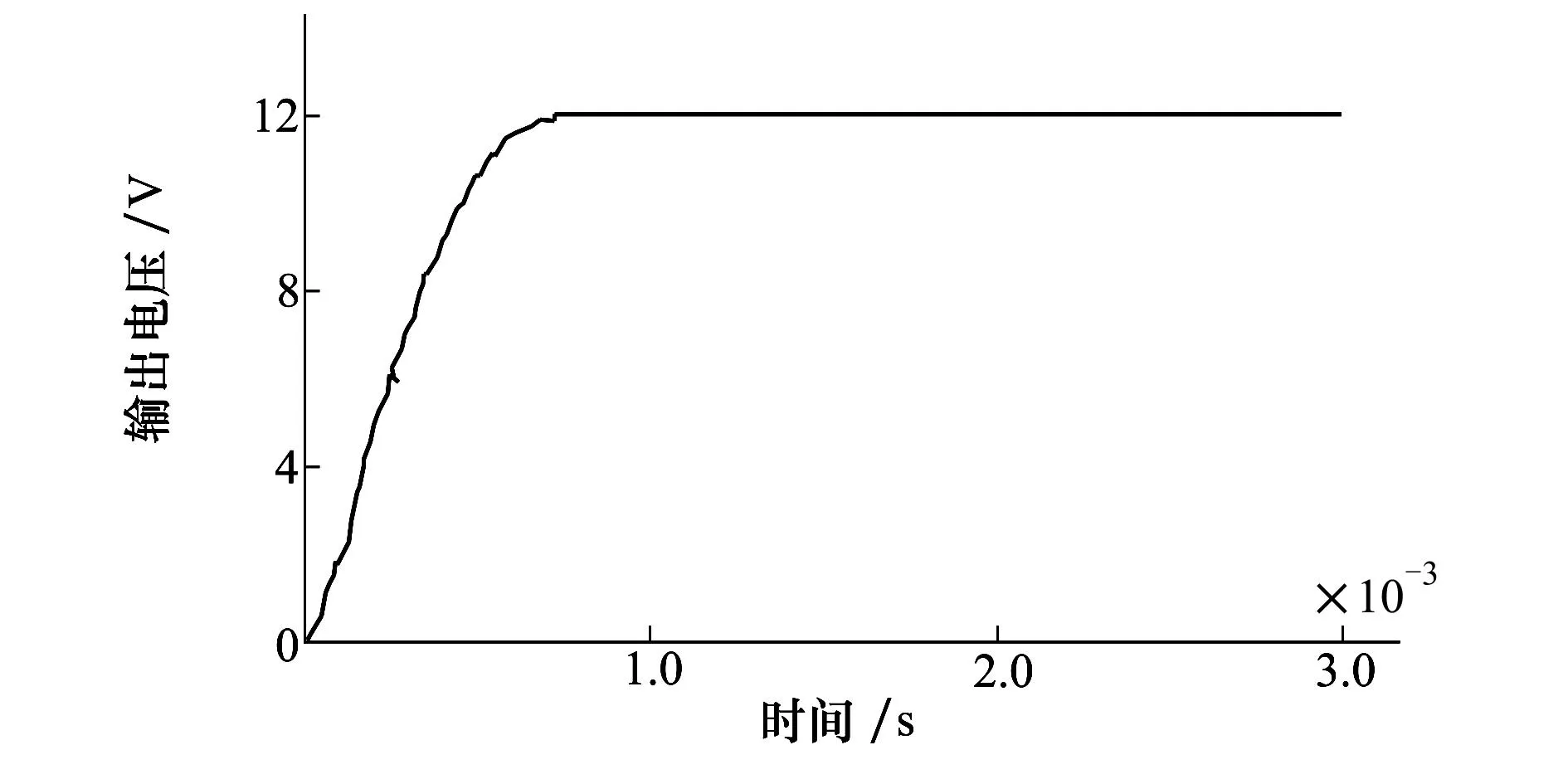
图4 PCL算法控制的变换器输出电压波形
根据图4可知,Buck变换器输出电压12V,调节时间为0.006 4s,电压纹波极小可忽略,无稳态误差,说明采用PCL算法控制的Buck变换器输出电压能很好的跟踪参考电压。
为说明PCL算法控制的Buck变换器输出的高精度,强鲁棒性和响应的快速性,从下面3个方面分别与PI和传统滑模进行对比:
4.1无扰动时变换器性能对比分析
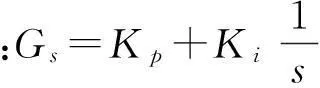
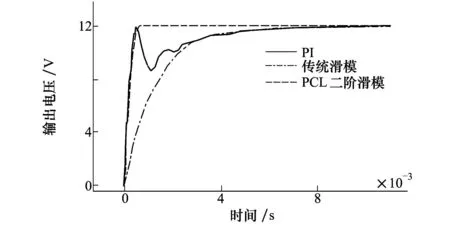
图5 Buck变换器输出电压过渡过程对比图

控制方法调节时间/s稳态电压/V电压纹波/VPI0.006012.0000.031传统滑模0.005611.8670.001PCL二阶滑模0.006412.0000.005
观察图5和表2,采用3种控制方法时输出电压调节时间相差较小,传统滑模控制时输出电压有0.133 V(1.1%)的静差,从PI,传统滑模到PCL二阶滑模控制,电压纹波逐渐减小。从稳态精度和响应快速性角度考虑,PCL二阶滑模算法的控制效果更佳。
4.2输入电压扰动时变换器性能对比分析
变换器输入电压在0.03 s时由24 V突然上升至48 V,电压增加100%。
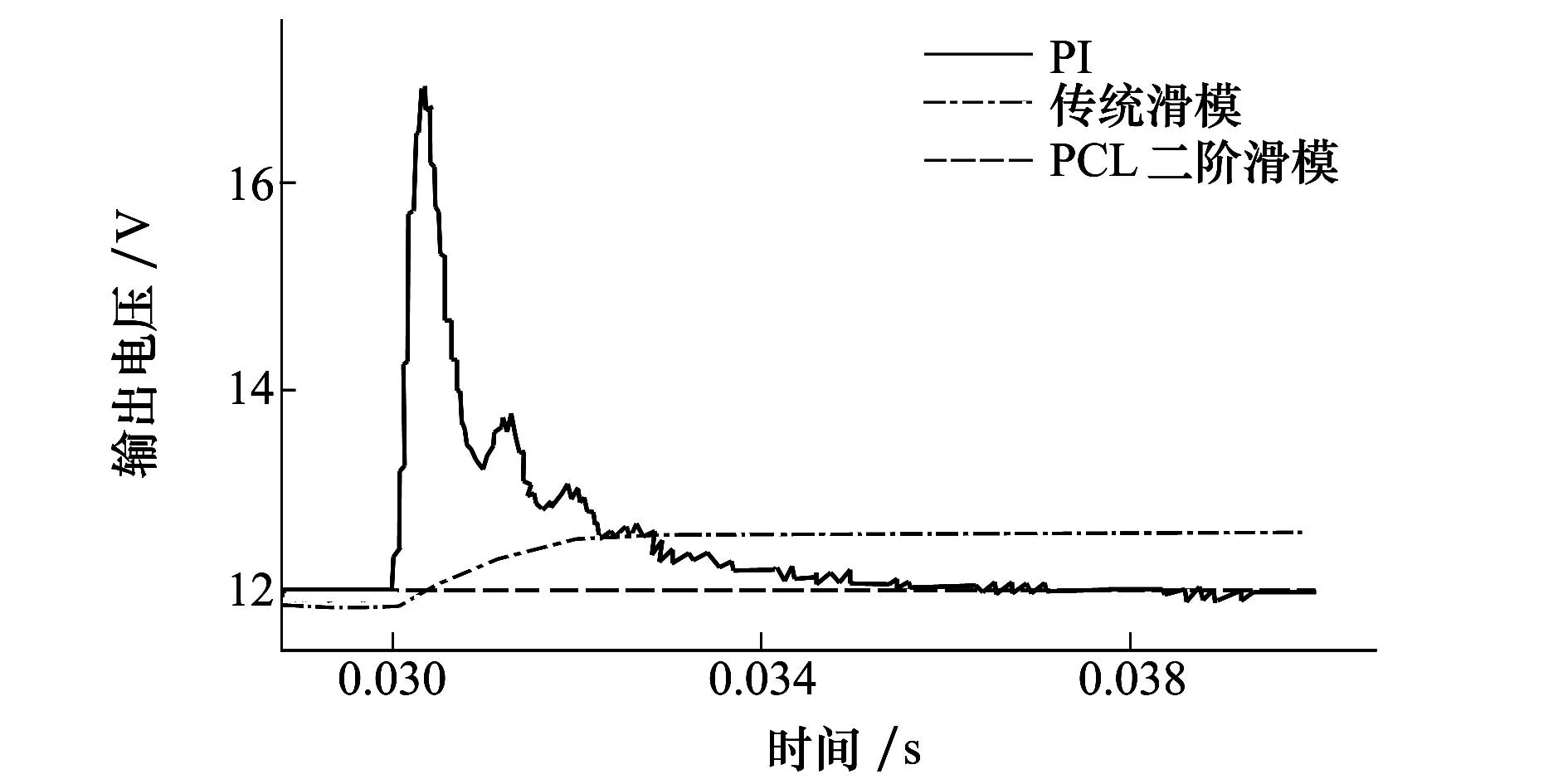
图6 Buck变换器输入电压扰动时输出电压对比图
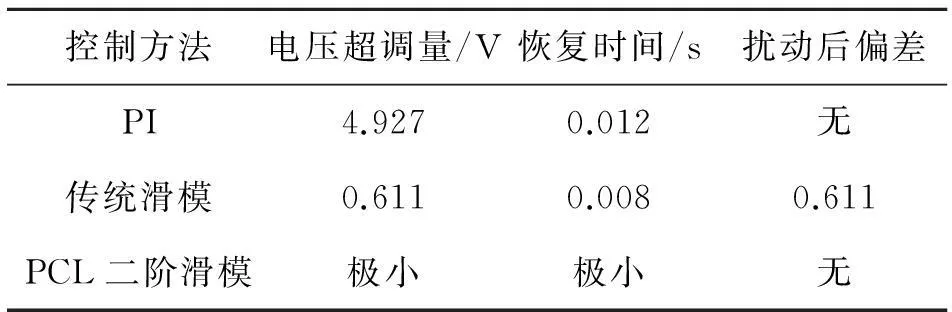
控制方法电压超调量/V恢复时间/s扰动后偏差PI4.9270.012无传统滑模0.6110.0080.611PCL二阶滑模极小极小无
观察图6和表3,在0.03 s输入电压发生扰动时,从PI,传统滑模到PCL二阶滑模控制,输出电压超调量和恢复时间逐渐减小。传统滑模在大扰动后输出电压有0.611 V(5.1%)的静差,而传统滑模本身存在1.1%稳态误差,由于扰动的原因,稳态误差大幅度增加。对比来看,PCL二阶滑模算法对输入干扰极不敏感,鲁棒性更强。
4.3负载电阻扰动时变换器性能对比分析
变换器负载电阻在0.05 s时由0.45 Ω下降至0.225 Ω,负载减少100%。
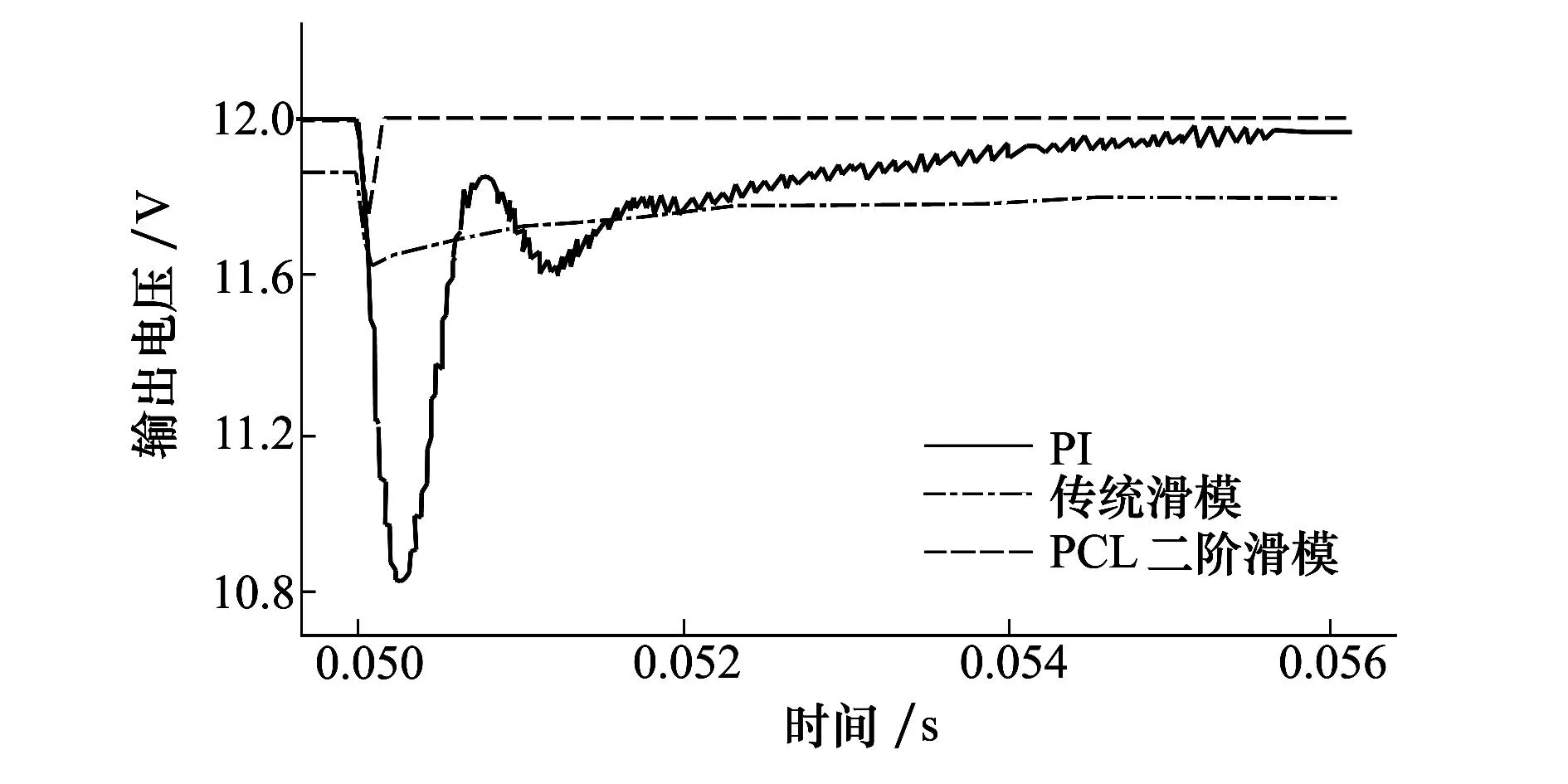
图7 Buck变换器负载电阻扰动时输出电压对比图
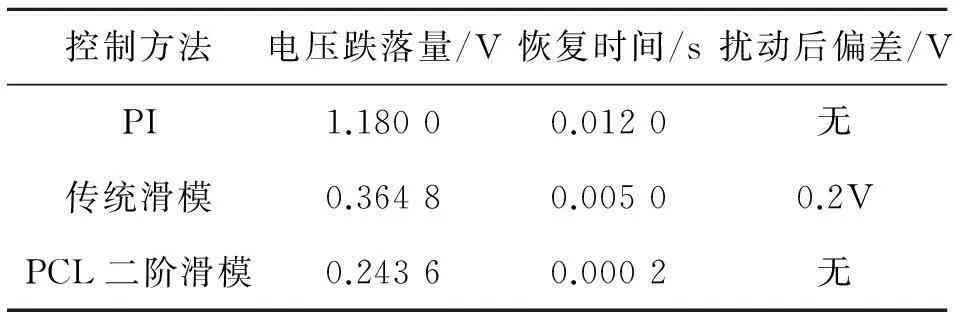
控制方法电压跌落量/V恢复时间/s扰动后偏差/VPI1.18000.0120无传统滑模0.36480.00500.2VPCL二阶滑模0.24360.0002无
观察图7和表4,在0.05 s负载电阻发生扰动时,从PI,传统滑模到PCL二阶滑模控制,输出电压跌落量逐渐减小。PCL二阶滑模控制时恢复时间明显少于传统滑模和PI、传统滑模扰动后输出电压相比期望值有0.2 V的静差,系统输出电压在扰动前本身具有。综上分析,PCL二阶滑模算法在大负载扰动时具有强鲁棒性,响应速度快的特点。
5结论
本文针对纯电动汽车上的DC-DC变换器,为提高系统在大扰动下的响应的快速性和鲁棒性,设计了一种基于prescribed convergence law算法的鲁棒滑模控制器。
以Buck变换器为例,prescribed convergence law算法能使系统输出电压很好的跟踪参考电压,并与PI和传统滑模控制效果进行对比。结果表明prescribed convergence law算法响应速度更快,精度更高,鲁棒性更强。
参考文献:
[1]嵇保健,赵剑锋.DC/DC 变换器数字控制方法研究[J].电力电子技术,2010,44(4):29-31
Ji Baojian, Zhao Jianfeng. Study on the Digital Control Methods for DC/DC Converter[J]. Power Electronic Technology, 2010,44(4):29-31 (in Chinese)
[2]马红波,冯全源.BUCK型开关变换器最优PID控制器设计[J].电机与控制学报,2008,12(6): 639-643
Ma Hongbo, Feng Quanyuan. Optimized PID Controller Design for Buck DC-DC Switching Converters[J]. Electric Machines and Control, 2008,12(6): 639-643 (in Chinese)
[3]Liu Jianxing, Laghrouche Salah, Harmouche Mohamed, Wack Maxime. Optive-Gain Second-Order Sliding Mode Observer Design for Switching Power Converters[J]. Control Engineering Practice, 2014, 30: 124-131
[4]Huangfu Y, Ma R, Mraoui A. Avoidance High-Frequency Chattering Second-Order Sliding Mode Controller Design:Buck Converter in Wind Power System[J]. International Journal of Antennas and Propagation, 2012, 2012(1): 1-5
[5]张涌萍,张波, 丘东元. DC-DC变换器双线性系统建模及基于李亚普诺夫直接法的控制方法[J]. 中国电机工程学报,2008,28(9):7-11
Zhang Yongping, Zhang Bo, Qiu Dongyuan. Bilinear System Model and Lyapunov-Based Control Method for DC-DC Converters[J]. Journal of Chinese Electrical Engineering Science, 2008,28(9): 7-11 (in Chinese)
[6]李军红,王飞,李君兰.变换器滑模控制的研究与实现[J].电源技术,2010,134(2):190-191
Li Junhong, Wang fei, Li Junlan. Research and Realization of Sliding Model Control for Buck Converter[J]. Power Technology, 2010, 134(2): 190-191 (in Chinese)
[7]皇甫宜耿,王毅,赵冬冬,等. 一种鲁棒高阶滑模super-twisting算法的全桥逆变器[J].西北工业大学学报,2015,33(2):315-319
Huangfu Yigeng, Wang Yi, Zhao Dongdong, et al. A Super-Twisting Algorithm of Robust High Order Sliding Mode Control for Full-Bridge Inverter[J]. Journal of Northwestern Polytechnical University, 2015,33(2):315-319 (in Chinese)
[8]皇甫宜耿,吴宇,马瑞卿.一种鲁棒无抖颤滑模控制的Buck-Boost变换器[J].西北工业大学学报,2014,32(2):285-289
Huangfu Yigeng, Wu Yu, Ma Ruiqing. A Robust Chattering-Avoiding Sliding Mode Control for Buck-Boost Converter[J]. Journal of Northwestern Polytechnical University, 2014,32(2):285-289 (in Chinese)
[9]Huangfu Yigeng, Wu Yu. A Robust Flyback Converter Based on High Order Sliding Mode Control for Fuel Cell[C]∥Industrial Electronics Society,IECON 2014-40th Annual Conference of the IEEE, 2014: 3936-3940
[10] Kumar A, Patil S L, Panday S K. Modeling and Control of DC-DC Buck Converter Using SMC[C]∥2015 International Conference on Industrial Instrumentation and Control, IEEE, 2015: 1406-1411
[11] Shtessel Y, Edwards C, Fridman L, et al. Sliding Mode Control and Observation[M]. Birkhäuser, New York, 2014
[12] Noori A, Farsi M, Esfanjani R M. Design and Implementation of a Robust Switching Strategy for DC-DC Converters[C]∥ IET Power Electronics, 2015
[13] Levant A. Higher-Order Sliding Mode, Differentiation and Output-Feedback Control[J]. International Journal of Control, 2003, 76(19): 924-941
PCL Sliding Mode Controller Design for Buck Converter under Large Disturbances
Xu Jiani, Huangfu Yigeng, Zhuo Shengrong, Pang Shengzhao
(Northwestern Polytechnical University, Xi′an 710072, China)
Abstract:On the basis of Prescribed Convergence Law(PCL) algorithm, this paper presents a robust sliding mode controller for the DC-DC converter in the pure electric vehicle in order to improve the rapidity and robustness under large disturbances.Taking Buck converter as an example, this paper verifies the convergence of the sliding mode algorithm in finite time, and compares it with PI and the traditional sliding mode control. The simulation results and their analysis show preliminarily that:① without disturbances PCL control has high steady state accuracy, short regulation time, and small output ripple,② under large disturbances in the input voltage and output load, PCL control shows faster response and stronger robustness.
Keywords:algorithms, computer simulation, controllers, convergence of numerical methods, DC-DC converter, design, diodes, electric vehicles, mathematical models, MATLAB, robustness(control systems), sliding mode control, topology, trajectories; buck converter, PCL(Prescribed Convergence Law) algorithm
中图分类号:TM423
文献标志码:A
文章编号:1000-2758(2016)01-0073-06
作者简介:许佳妮(1993—),女,西北工业大学硕士研究生,主要从事电源变换技术研究。
基金项目:航空科学基金(2014ZC53037)与高等学校博士学科点专项科研基金(20126102120050)资助
收稿日期:2015-10-28
