非定常求解的内迭代初值对计算效率的影响研究

贡伊明, 张伟伟, 刘溢浪

(西北工业大学 航空学院, 陕西 西安　710072)



非定常求解的内迭代初值对计算效率的影响研究

贡伊明, 张伟伟, 刘溢浪

(西北工业大学 航空学院, 陕西 西安710072)

摘要：基于非定常流场的双时间求解方法,提出了一种提高非定常流场求解效率的有效策略。通过对前几个时刻的流场信息进行外插来确定下一时刻的迭代初值,使之更接近于收敛解,降低内迭代初始残值,进而提高了非定常流场的求解效率。将流场中每个点的守恒量在时间方向上进行泰勒级数展开,设计了若干种外插格式。采用绕圆柱非定常流动的求解来验证本方法的计算效果,并研究了不同初值外插格式、空间离散格式、时间步长和收敛标准对初值外插方法效果的影响。研究表明,在双时间步法基础上,采用初值外插策略可普遍提高计算效率,其中交替外插策略可以普遍将求解效率提高1倍左右。相比于迎风格式,该方法对中心格式的求解效率提高更显著,并且对于不同的收敛标准和时间步数均有非常明显的效果。

关键词：初值外插;非定常流场求解;泰勒级数展开;双时间步法

近些年来,随着计算机性能的提高,计算流体力学(computational fluid dynamics,简称CFD)在很多工作中得到广泛运用。在实际的工程应用中,很多问题涉及到非定常流动,并且其计算量远大于定常流动,比如,气动弹性动力学问题、涡轮叶片绕流问题、分离涡脱落问题、动导数的求解等等。由此而促进了各种加速收敛技术和时间推进格式的发展。

为了提高计算效率,前人发展了很多加速收敛措施,如当地时间步长、隐式残值光顺方法和多重网格方法[1]。隐式时间推进方法可以在保证稳定性的同时大幅提高时间步长,进而提高计算效率,常用的有近似因子分解(AF)[2]、超松弛迭代方法(SSOR)[3]、直接求解方法和Newton-Krylov方法[4]。在近似因子分解方法中应用最广的是LUSGS算法[5]。后来Chen和Wang[6]对LUSGS进行了改进,在有限体积方法中发展了BLUSGS算法。Newton-Krylov方法中最受欢迎的是Newton-GMRES[7],其中无矩阵存储的GMRES方法[8]在CFD中应用更为广泛。

非定常流场的计算方法可分为2大类:双时间步方法(dual-time stepping)和物理时间迭代方法(physical time subiteration)。双时间步法引入了伪时间项,对于每一个物理时刻看做定常流动来求解。双时间步法的好处是原来用于定常计算的预处理、当地时间步、对角化、多重网格都可以应用到计算中;真实时间步长可以取得很大;双时间法可以降低通量线性化误差和近似因子分解误差,放宽了稳定性限制[9]。这些方法都能有效的提高收敛速度。

流场求解效率不仅仅与收敛速度有关,还与初值与收敛解间的差距有关。因此,在基于双时间方法的非定常流场求解中,为了提高计算效率,通常将上一个时刻的流场作为下一个时刻流场求解的初值。至于从初值角度进一步提高计算效率,相关研究鲜有报道。本文从该研究角度出发,将前2～3个物理时刻的流场信息外插求解出待求时刻的流场作为伪时间步迭代的初场,这样就进一步缩小了初值与收敛解的差距,以期减小迭代步数,提高计算效率。

基于以上的思想,本文通过采用内迭代初值外插,发展了一种提高非定常流场求解效率的有效策略。采用绕圆柱非定常流动的求解算例来验证本方法的计算效果,并研究了不同初值外插格式、空间离

散格式、时间步长和收敛标准对初值外插方法效果的影响。

1数值方法

1.1双时间步方法

为了提高非定常流场的时间计算精度,同时又要求具有较高的计算效率,Jameson 提出了一种双时间步方法,即在冻结的物理时间点上加入类似 Newton 迭代的虚拟时间迭代过程,通过增加内迭代过程提高 LU-SGS 等隐式线性化方法所损失的时间精度。双时间步法思想简单,且在定常流计算程序基础上进行改造的工作量小,得到了广泛应用,其实现形式如下。

非定常流动控制方程离散后的形式为

(1)

(2)

这里的Qn表示第个物理时间步的守恒量,Δt代表物理时间步长。

方程(2)直接求解比较困难,双时间步法采用虚时间迭代技术对方程(2)进行求解,引入一个虚拟时间τ,将控制方程(2)改写为

(3)

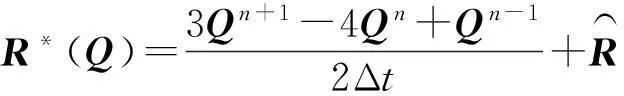
(4)

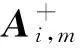
1.2初值外插方法

初值外插方法是通过记录前几个时刻的流场的基本信息进行外插得到下一个物理时刻的内迭代初值。

一般情况下,采用外插时必须要保证插值对象的连续性。若其出现比较强的间断,则外插出现的偏差往往会比较大,这样就会与我们的初衷背道而驰。因此,合理选择外插对象至关重要。相对于原始变量,守恒变量的连续性更好,因此我们将流场的守恒量进行外插。但对于流场本身存在强间断情况,比如有激波出现,此时用初值外插方法容易造成更大偏差,不宜使用。在时间方向上的泰勒级数展开如下:

(5)

如果时间方向上取一阶精度,时间导数采用一阶向后差分,即

(6)

代入(5)式并忽略二阶项可得一阶外插格式

(7)

同样的,如果时间方向上取二阶精度,一阶时间导数采用中心差分, 二阶导数采用二阶向后差分并忽略三阶项可得二阶外插格式

(8)

同理可得三阶精度的外插格式

(9)

本文还提出了一阶与三阶交替的外插格式。即在第n个物理时刻,取2m为周期有:

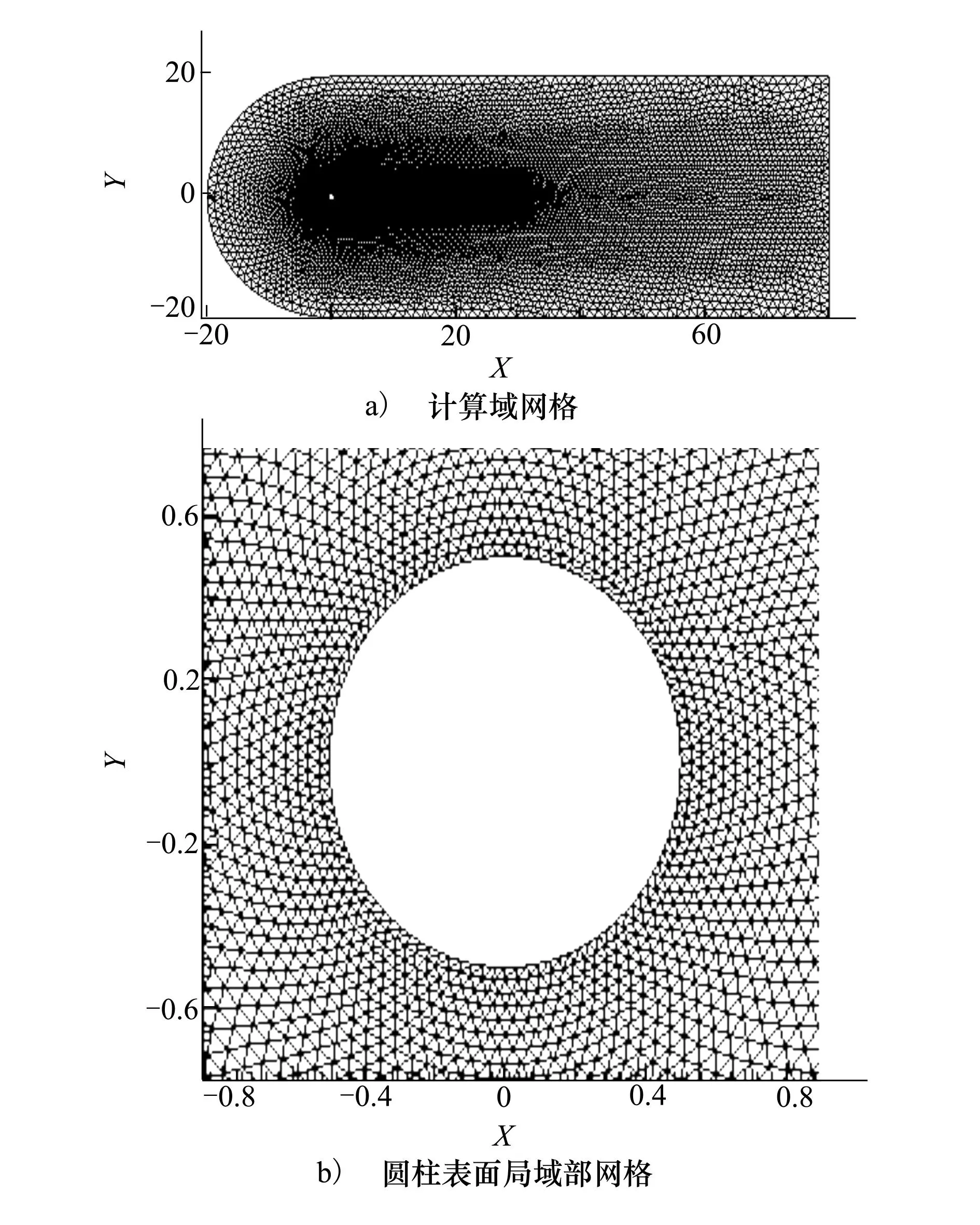
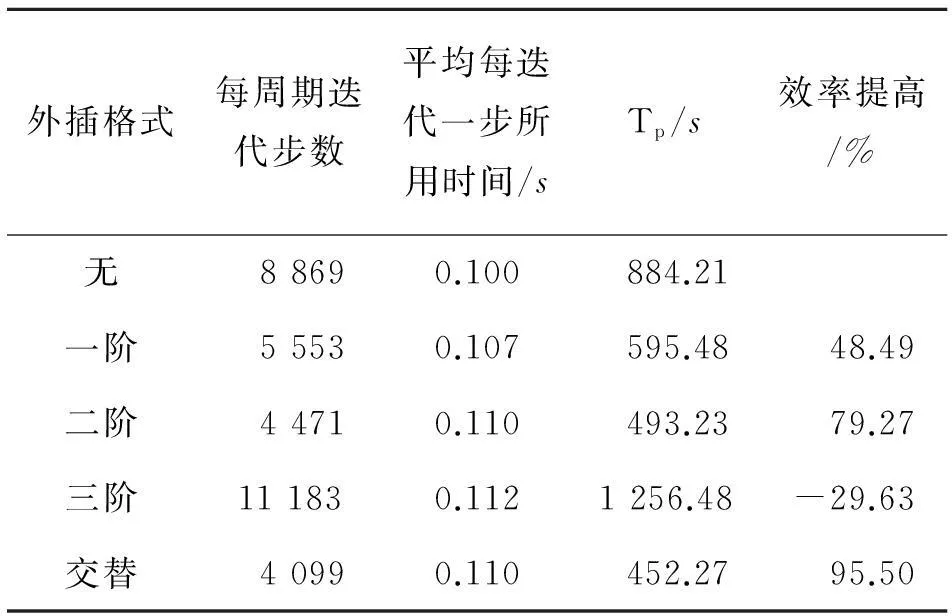
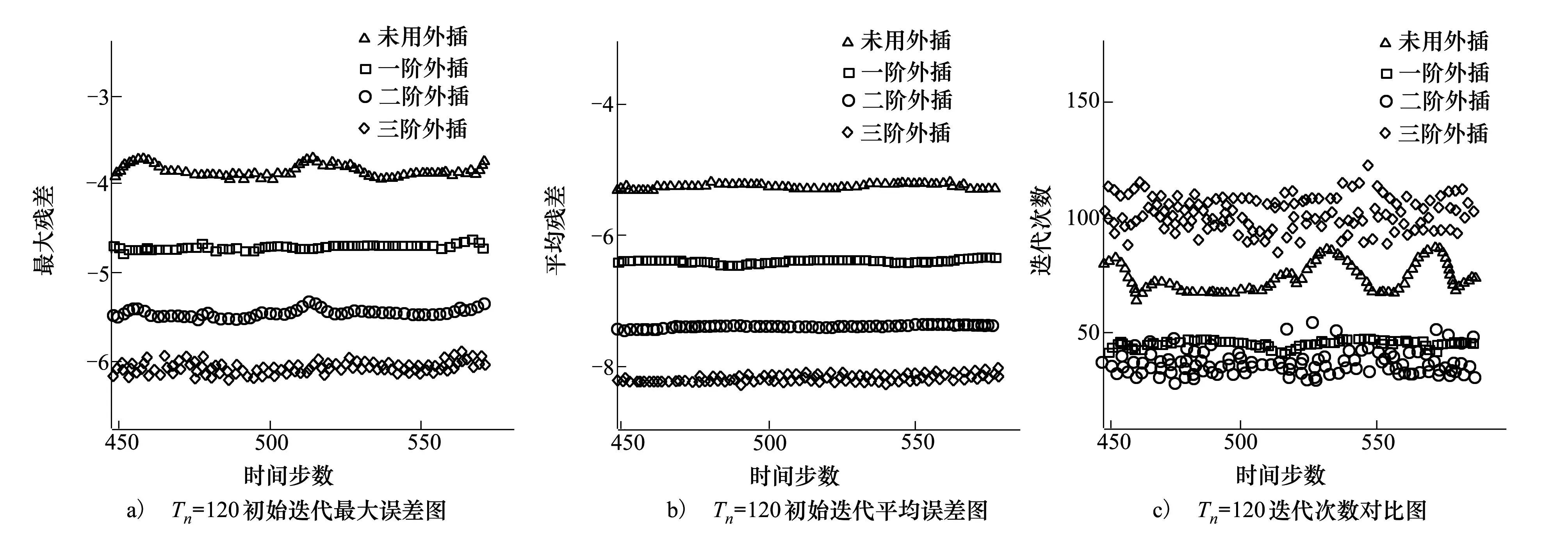
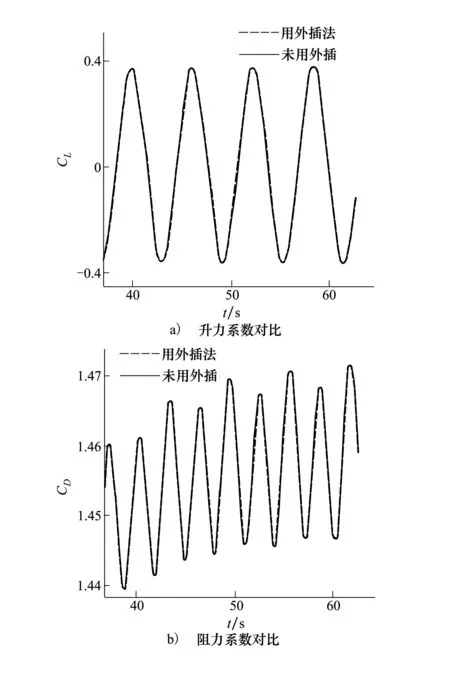
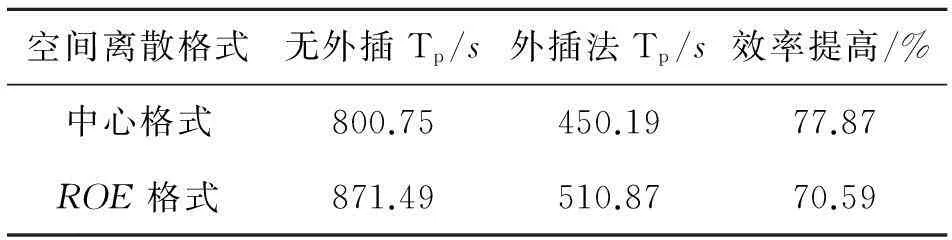
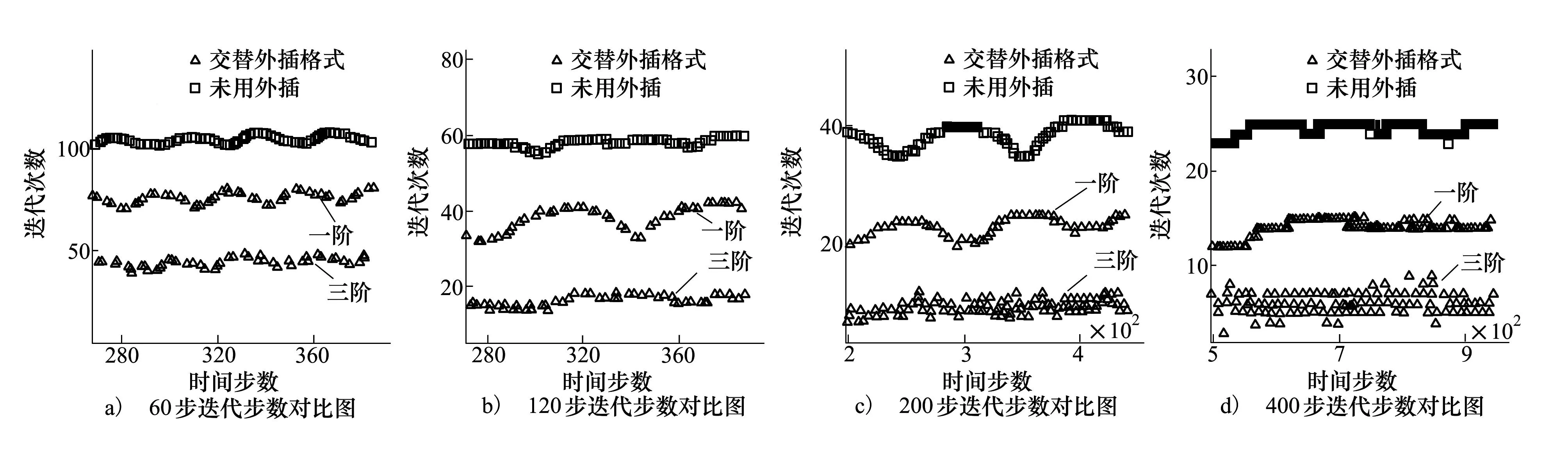
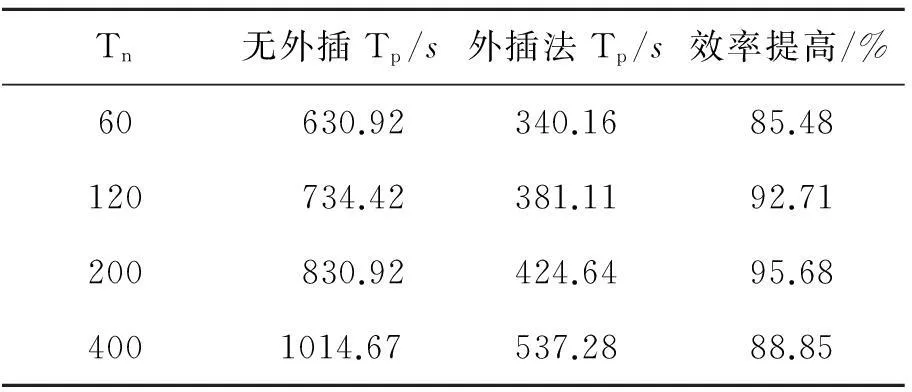
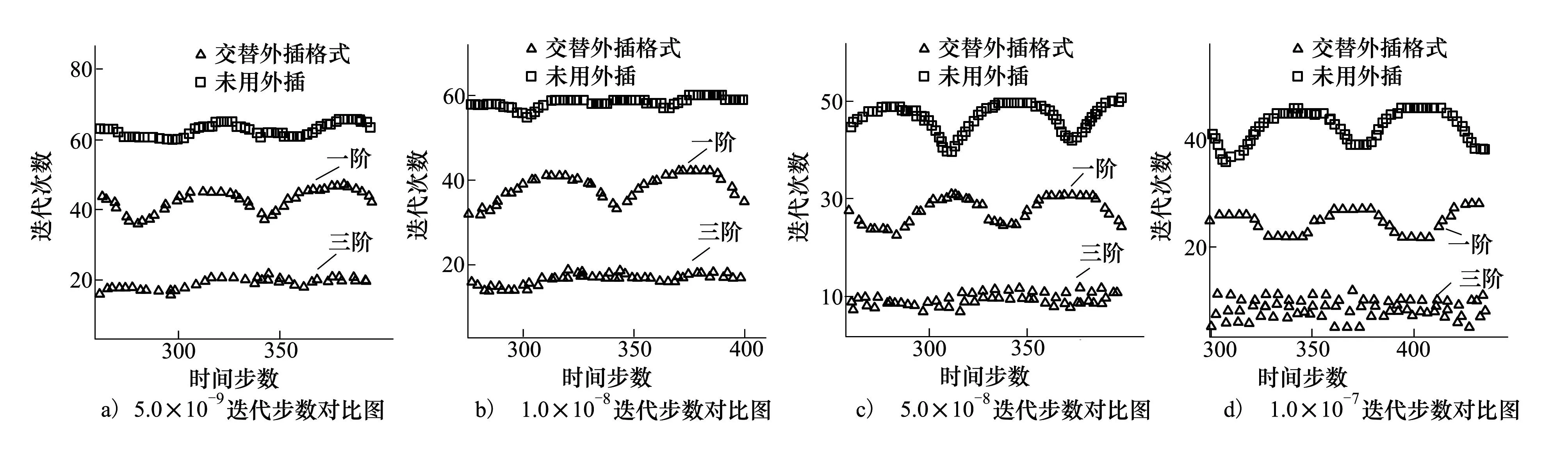
若mod(n,2m)

若mod(n,2m)>m-1,则下一时刻的初值为Qn+1=4Qn-6Qn-1+4Qn-2-Qn-3

根据多次计算对比结果,取m=3时效果更好。因此后面的交替外插都采用的是每6个时间点为1个周期,三步一阶外插三步三阶外插的格式。

2数值算例验证

2.1算例介绍

以非定常静止圆柱绕流为例,对于不同外插格式和空间离散格式下的初值外插方法进行效率对比并分析时间步长和收敛标准对初值外插方法效率的影响。来流马赫数为0.1,雷诺数为100,层流,采用非结构三角形网格,圆柱表面网格节点数为100,网格总数为29 788,计算域网格和圆柱表面局部网格示意图如图1所示。

图1　层流圆柱绕流计算网格示意图

2.2不同因素影响对比

在初值外插方法介绍中给出了一阶、二阶、三阶和交替外插4种外插格式。本节针对采用不同的外插格式、空间离散格式对初值外插方法效率的影响进行分析并确定使该方法效率最好的外插格式和空间离散格式,并分析不同的时间步长和收敛标准对初值外插方法效率的影响。

在非定常圆柱绕流算例中,空间离散采用中心格式,取时间步长为1个周期120步,设1个周期的步数为Tn,则有Tn=120。设每个周期平均耗时为Tp。收敛要求为最大残值小于5.0×10-9。具体状态在2.1节中已经交代。对一阶、二阶、三阶和交替外插精度的外插效果进行对比。以下是计算结果:

表1　4种格式效率对比表

图2　不同外插精度计算效果图

由图2可以看出,无论是初始迭代的最大误差还是平均误差,均随着外插精度的提高而降低。而迭代步数并不满足该规律,初始迭代误差最小的三阶精度外插的迭代步数反而是最多的,换而言之,采用三阶精度外插格式会出现收敛困难的现象。对于出现收敛困难现象的原因,在下一节中会具体分析。

从表1中不难看出一阶精度、二阶精度和交替外插格式均可明显减少每周期迭代步数,但由于采用初值外插方法每一步迭代增加了计算量和存储因而每一步迭代所用的时间会有所增加。比较后发现平均每迭代一步所用的时间增加量很小,大约10%左右。因此整体的效率仍然是提高的。在4种格式中采用三步一阶三步三阶的交替外插格式效率最高。因此,本文后面的计算没有特殊说明均采用三

图3　采用初值外插法前后的升力与阻力系数对比

步一阶三步三阶的交替外插格式。从图3中可以看出采用初值外插方法前后计算结果完全吻合,证明了初值外插方法的准确性。

采用不同的空间离散格式,分析对初值外插方法的效率是否会有所影响以及影响程度如何。本文对比了中心格式和迎风ROE格式2种空间离散格式,时间步长取1个周期120步,收敛标准为5.0×10-9。以下是对比结果:

表2　不同空间离散格式计算效率表

从表2中可以看出采用不同的空间离散格式对于初值外插方法效率会有一定的影响。空间离散采用中心格式初值外插方法的效果更好。对比中心格式和迎风格式不难发现,中心格式利用了较多的网格系统作为模板,因此对于模板的迭代初值更为敏感。当迭代初值更接近收敛解时,采用中心格式比采用迎风格式提高的效率就会更多。

时间步长和收敛标准选取的不同对初值外插方法的效率也会有所影响。本文通过改变时间步长和收敛标准观察初值外插方法的效率变化情况。

不改变其他的参数,仅对时间步长进行改变,分析对该方法效率的影响。以中心格式为例,对于时间步长分别取1个周期60步、120步、200步和400步的情况,收敛标准为最大残值小于1.0×10-8。图4和表3显示了初值外插方法的效率变化情况。

图4　不同时间步长初值外插法迭代步数图

Tn无外插Tp/s外插法Tp/s效率提高/%60630.92340.1685.48120734.42381.1192.71200830.92424.6495.684001014.67537.2888.85

从以上图表中不难看出,时间步长的改变虽对外插方法的计算效率提升量有一定影响,但影响不大。因此,可以认为在很大的时间步数变化范围内初值外插方法均有非常明显的效果。

下面研究收敛标准对外插方法效率提升的影响。空间离散采用中心格式,固定时间步长为1个周期120步,收敛标准分别取最大误差小于5.0×10-9、1.0×10-8、5.0×10-8和1.0×10-7时观察初值外插方法的效果。

图5　不同收敛标准初值外插法迭代步数图

收敛标准无外插Tp/s外插法Tp/s效率提高/%5.0×10-9884.21452.2795.501.0×10-8728.50354.17105.695.0×10-8642.26289.72121.681.0×10-7609.29262.40132.20

从以上图表中可以看出在一定范围内随着收敛标准降低,初值外插法的效率会提高。但即使对于高精度的数值求解,初值外插法的效率仍然可以将效率提高将近一倍。因此初值外插法对于不同精度的求解均具有非常明显的效果。

2.3流场误差传播分析

一般情况下,外插精度越高,流场迭代初值与收敛解越接近,初值外插方法计算效率就越高。然而三阶精度外插的计算效率却最低,甚至还没有不用初值外插方法的效果好。产生这种现象的原因归结于误差的2个分量。

不同的初值与真实解的误差可以按照误差各个傅里叶分量的衰减程度不同,分为高频振荡误差和低频光滑误差。

在线性空间内任何初始误差均可表示为

(10)

式中，E0为初始误差,vi表示第i个特征向量,ai表示误差第i个分量对应的系数。

在迭代过程中

(11)

很明显,特征向量代表误差分量,其对应的特征值代表误差分量的放大系数。误差每一个分量vi都对应一个误差频率k,当1≤k

高频振荡误差是局部行为,来源于附近几个网格点之间的相互耦合,与边界距离较远的网格点的信息无关;而低频光滑误差是全局行为,主要来源于边界信息。通过局部松弛后误差呈现光滑性,此时误差主要来自于边界。可以设想二维N×N网格上的点松驰方法, 将边界信息传播到所有点至少需O(N)次迭代, 因此收敛速度极慢。低频光滑误差量阶很小,但在细网格上很难收敛[13]。

在迭代过程中低频误差的大小与迭代初值和迭代格式有关。采用初值外插方法会对迭代初值进行改变,低频误差的大小也会随之发生变化。在外插过程中,不仅仅是对精确解的插值,由于收敛标准的限制,存在一定的误差,因此外插的对象还包括残余的误差。高精度外插对插值对象的连续性要求较高,而残余误差的变化本身具有随机性与不连续性。低频误差由于在迭代过程中难以收敛在残余误差中占有较高的比例。通过高阶精度外插格式得到的初始迭代误差比低阶精度外插格式小,但是高阶精度外插格式只可以大幅衰减高频误差,低频误差反而被放大,低频误差收敛速度极慢因此高精度外插会出现收敛困难情况。

一阶外插能够保证误差变化的单调性,不会出现低频误差的放大。但是精度较低,高频误差分量衰减幅度小;高阶外插虽然可以大幅度衰减高频误差,但是会出现低频误差的放大。通过采用三步一阶三步三阶的交替外插格式,既可以大幅衰减高频误差分量,又能保证低频误差不会被放大。

3结论

本文在非定常流场双时间步法求解的基础上,提出了将前2～3个物理时刻的流场信息外插求解出待求时刻的流场作为伪时间步迭代初场的初值外插方法,并通过绕圆柱非定常流动算例验证了本方法的有效性,研究结果显示:

1) 相对统一精度的外插格式,交替精度的外插格式具有更高的鲁棒性和计算效率,可普遍将计算效率提高一倍左右。

2) 不同的空间离散格式对初值外插方法的效果有一定的影响,相对于迎风格式,中心格式采用初值外插方法的效率会更高。

3) 初值外插方法的效率提升量会受时间步长和收敛标准影响,但在较宽的时间步长和收敛标准范围内,效率提升仍十分可观。

参考文献：

[1]燕振国. 高精度混合线性紧致格式的隐式时间推进方法研究[D]. 成都: 中国空气动力研究与发展中心, 2013

YanZhenguo.InvestigationofImplicitTimeIntegrationMethodswithHDCSSchemes[D].Chengdu:ChinaAerodynamicsResearchandDevelopmentCenterGraduateSchool, 2013 (inChinese)

[2]PulliamTH,ChausseeDS.ADiagonalFormofanImplicitApproximate-FactorizationAlgorithm[J].JournalofComputationalPhysics, 1981, 39: 347-363

[3]YoungDM.AHistoricalReviewofIterativeMethods[C]∥TheACMConferenceonHistoryofScientificandNumericComputation, 1987

[4]LomaxH,PulliamTH,ZinggDW,etal.FundamentalsofComputationalFluidDynamics[M].Springer,Berlin, 2001

[5]YoonS,JamesonA.Lower-UpperSymmetricGauss-SeidelMethodfortheEulerandNavier-StokesEquations[J].AIAAJournal, 1988, 26: 1025-1026

[6]ChenRF,WangZJ.Fast,BlockLower-UpperSymmetricGauss-SeidelSchemeforArbitraryGrids[J].AIAAJournal, 2000, 38: 2238-2245

[7]MichalakC,Ollivier-GoochC.GlobalizedMatrix-ExplicitNewton-GMRESfortheHigh-OrderAccurateSolutionoftheEulerEquations[J].Computers&Fluids, 2010, 39: 1156-1167

[8]KnollDA,KeyesDE.Jacobian-FreeNewton-KrylovMethods:aSurveyofApproachesandApplications[J].JournalofComputationalPhysics, 2004, 193: 357-397

[9]赵慧勇, 乐嘉陵. 双时间步法的应用分析[J], 计算物理, 2008, 25(3): 253-258

ZhaoHuiyong,LeJialing.ApplicationAnalysisonDual-TimeStepping[J].ComputationalPhysics, 2008, 25(3): 253-258 (inChinese)

[10]JamesonA.TimeDependentCalculationsUsingMultigridwithApplicationstoUnsteadyFlowsPastAirfoilsandWings[C].AIAAPaper91-1596, 1991

[11] 王刚. 复杂流动的网格技术及高效、高精度算法研究[D]. 西安: 西北工业大学, 2005

WangGang.NewTypeofGridGenerationTechniquetogetherwiththeHighEfficiencyandHighAccuracySchemeResearchesforComplexFlowSimulation[D].Xi′an,NorthwesternPolytechnicalUniversity, 2005 (inChinese)

[12] 刘超群. 多重网格法及其在计算流体力学中的应用 [M]. 北京: 清华大学出版社, 1995

LiuChaoqun.MultigridmethodwithApplicationtoComputationalFluidDynamics[M].Beijing,TsinghuaUniversityPress, 1995 (inChinese)

[13] 李晓梅, 莫则尧. 多重网格算法综述[J]. 中国科学基金, 1996, 10(1): 4-11

LiXiaomei,MoZeyao.ViewpointsofMultigridAlgorithms[J].BulletinofNationalScienceFoundationofChina, 1996, 10(1): 4-11 (inChinese)

Researching how Initial Value of Internal Iteration Impacts on Computational Efficiency in Unsteady Flow Solving

Gong Yiming, Zhang Weiwei, Liu Yilang

(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:On the basis of the dual time stepping method in unsteady flow, we come up with a strategy to improve the efficiency in unsteady flow solving. By means of extrapolating the flow message of a few moments forward, we get the iterative initial value of the next moment to make it closer to the convergent solution and decrease the initial residual value of internal iteration, thus increasing the computational efficiency of unsteady flow. Taylor expand the convective term of flow field in time direction, then we design some kinds of extrapolation schemes. We use the solution of unsteady flow around circular cylinder to verify the computational efficiency of this method, and research on different initial value extrapolation schemes, spatial discretization schemes, and time steps and convergence criteria impacting on the efficiency of initial value extrapolation method. Researches show that based on the dual time stepping method, using the strategy of initial value extrapolation can improve the computational efficiency generally. Of which the alternate extrapolation strategy can doubled the efficiency generally. Compared with upwind scheme, the efficiency of this method increases more when using center scheme; all have obvious effects when using different time steps and convergence criteria.

Keywords:computational efficiency, design, dual time stepping method, errors, extrapolation, flow fields, iterative methods, laminar flow, Mach number, mesh generation, Reynolds number, initial value extrapolation, unsteady flow solving, Taylor series

中图分类号：V211.3

文献标志码：A

文章编号:1000-2758(2016)01-0011-07

作者简介：贡伊明(1993—)，西北工业大学硕士研究生，主要从事计算流体力学研究。

收稿日期：2015-09-18