网络化城市轨道交通时刻表换乘协调优化研究

白广争， 郭 进，石红国，杨 扬，张太花

(1.西南交通大学 信息科学与技术学院，四川 成都 610031；2.西南交通大学 交通运输与物流学院，四川 成都 610031；3.成都地铁运营有限公司,四川 成都 610031)

随着城市内轨道交通线路的不断增加，网络化运营模式已经成为一种趋势，网络中线路之间的相互影响也越来越显著。为了减少乘客在换乘站的滞留时间，需要对各线路的行车组织进行合理规划，加强线路间列车运行的衔接协调，进而提高整个轨道交通网络客流的畅通性。因此，优化换乘站列车的衔接关系，对提高乘客换乘效率、降低乘客出行时间及提高乘客服务水平具有重要意义。

单个换乘站的协调是根据换乘站内客流到达特征，对经过该站的各方向列车的到发时刻进行协调，使其形成良好的接续关系[1-7]，从而实现降低换乘站乘客候车时间的目的。而在网络化的运营环境中，由于列车在线路上各站之间的运行时间及各车站的停站时间具有相对确定性，虽可适当调整，但调整幅度有限，因此，列车在不同换乘站的到发时刻之间存在一定的相互制约关系。针对单个换乘站的协调优化结果放在网络中会出现运行时间冲突的问题，要求换乘站之间的协调与换乘站内各运行方向上的衔接协调结合起来，才能制定出行之有效的优化方案。

在网络化的运营条件下，既要考虑单线路的行车条件要求，将协调对单线路的行车组织影响降至最低，又要实现全路网乘客换乘等待时间最少，因此，城市轨道交通时刻表换乘协调工作是一个多目标多约束问题。本文分析单个换乘站中各方向运行列车的接续问题，得出换乘站客流的总换乘等待时间计算方法；考虑在网络化运行条件下换乘站间列车运行时间的调整问题，以网络中乘客总换乘等待时间最少及换乘站间列车运行时间调整最小为目标，建立多目标优化模型；设计非支配排序进化算法(Non-dominated Sorting Genetic Algorithm Ⅱ，NSGA-Ⅱ) 求解问题，并通过实例进行验证。

1 条件假设与符号说明

1.1 条件假设

设所协调时段为[ta，tb]，为了降低问题复杂性，对运行条件作如下假设：

(1)线路上、下行列车独立运行，各自到达与离开换乘站的时刻相互没有制约关系。

(2)乘客均能乘上所遇到的第一趟换乘列车，不会因为拥挤而错过，即运能是充足的。

(3)协调时段内，各线路列车采取均衡行车方式。

(4)同一线路的上、下行之间不产生换乘关系。

(5)列车的区间运行时间与车站停站时间可做适当调整。

1.2 符号说明

为了方便问题描述，对网络中某一个确定换乘站的运行参数作如下符号说明。

Rij：线路i的j方向，j=1，2。其中j=1表示上行；j=2表示下行；i=1，2，…，n。其中n为经过该换乘站的线路数。

nijs：[ta，tb]内，Rij方向上共开行的列车对数。

Aij：[ta，tb]内Rij上各列车到达该换乘站的时刻集合。

Dij：[ta，tb]内Rij上各列车在该换乘站的停站时间集合。

Lij：[ta，tb]内Rij上各列车驶离该换乘站的时刻集合。

hij：[ta，tb]内Rij上各列车的行车间隔。

M：[ta，tb]内该换乘站所有接续关系的集合。即：M={Rij→Rpq︱i≠p；i，p∈{1，2，…，n}；j，q∈{1，2}}。

对于网络化环境中，运行参数做如下设定：

U：网络中换乘站集合，存在Um、Un∈U。

S：网络中换乘站总个数。

2 单个换乘站乘客换乘等待时间计算

列车在线路上采取等间隔方式运行，则会在换乘站内形成稳定的“衔接周期”[1]，即当相交的两条线路上列车行车间隔分别为h1和h2时，则这两条线路在换乘站内以lcm(h1，h2)为周期形成衔接关系。文献[1]分析了“衔接周期”内乘客换乘总候车时间的计算方法，并以该值最小为优化目标。但是，在实际运营过程中，每趟列车带来的换乘客流量各不相同，乘客在每个“衔接周期”内的到站量分布并不一定相同，因此，在一个“衔接周期”内乘客换乘总候车时间最少并不能代表在其他“衔接周期”内的换乘乘客总等待时间也最少。因此，本文计算协调时段换乘站内所有换乘乘客的总候车时间，并做为网络化运营协调的基础。

为了计算单个换乘站内乘客的总换乘候车时间，首先应确定与换乘站相关的列车运行基本参数，包括到发时刻的表示及各参数受到的约束；然后计算一个换乘接续方向上所有乘客的换乘等待时间；最后，对各接续方向乘客换乘候车时间求和，即可得出换乘站中所有换乘乘客的候车时间表达式。

2.1 换乘站列车到发时刻分析

nij=0，1，2，…，nijs-1

( 1 )

式( 1 )中，nij满足

( 2 )

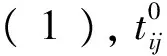
( 3 )

根据Rij上列车的离站时刻集合Lij和列车停站时间集合Dij，可以确定列车的到站时刻集合Aij为

( 4 )

2.2 线路间换乘接续关系分析

( 5 )

相邻两趟列车离站时刻满足

( 6 )

( 7 )

( 8 )

2.3 换乘站内乘客总候车时间计算

以上求得一个换乘接续方向上所有换乘乘客的候车时间。而在换乘站中通常会存在多个换乘接续方向，因此，对各接续方向乘客候车时间求和可得站内乘客换乘总候车时间为

( 9 )

3 网络化运营条件下列车运行协调优化

网络化运营条件下，换乘站的协调比单个换乘站的协调优化问题增加了换乘站之间列车运行时间及停站时间的影响，根据第2节研究所得出的单个换乘站列车离站时刻协调结果，放在网络中往往会造成换乘站之间运行时间的冲突，列车在线路上运行，无法同时满足多个换乘站各自计算的离站时刻要求。为了协调换乘站之间的离站时刻，需要对线路上车站间的运行时间及各站停站时间做一定调整。由于平峰时段网络中各线路行车间隔基本较大，因此适当调整列车站间运行时间和停站时间的方案是可行的。调整的依据是相邻换乘站Um、Un之间的运行时间TUm→Un和TUn→Um，使其满足

(10)

或者

(11)

图1 换乘站位置关系

TUm→Un由Um→Un的车站停车时间和区间运行时间组成，即

(12)

TUn→Um同理可得

(13)

(14)

(15)

为了避免调整对原有运行时间的影响过大，要求列车运行参数调整的幅度越小越好。

根据以上分析可以得出，网络条件下运行协调的第一目标是使得整个网络中在协调时段内乘客总换乘等待时间最小，如式(16)所示，即

Obj 1:

(16)

协调的第二目标是换乘站站间运行时间及停站时间调整最少，以调整后与调整前的运行时间方差来表示，则运行调整应满足

Obj 2:

(17)

式中：TUm→Un(0)表示调整前相邻换乘站之间列车的运行时间；TUm→Un表示调整后相邻换乘站之间列车的运行时间；lx表示共需要调整的换乘站间运行时间的数量。

根据以上分析，得出网络条件下线路间衔接性协调优化模型。其中式(16)、式(17)为模型目标，式( 1 )～式(15)为模型约束条件及参数间关系描述。在求解目标(16)的过程中参考第2节单个换乘站乘客等待时间的求解过程。

4 算法设计

网络化换乘站协调优化模型包含两个目标，属于多目标优化问题(MOP)。在求解MOP时，通常采用两类方法：其一为首先按照某种策略确定多种目标之间的权重，然后将多目标问题转化为单目标问题的传统求解方法，如加权求和法、理想点法等，最终求解单目标的优化解；其二为采用一些近代智能搜索算法，如NSGA、NSGA-Ⅱ、PAES、PESA、SPEA等，通过搜索多个目标的非劣(又称Pareto)解，找出可接受的“不坏”解[8]供决策者参考，实现多目标优化。多目标优化问题一般不存在单个最优解，而是一个Pareto解集。在众多的多目标进化算法中，NSGA-Ⅱ算法是目前处理2～3个优化目标中最优秀的算法之一，本文设计NSGA-Ⅱ算法求解。

采用实数编码方式，编码对象为各个换乘站内的各方向上列车在协调时段内的初始离站时刻，进化过程中的选择操作设置为二元锦标赛模式，赛制规模取2。为了简化设计，本文采取算术交叉策略，设计交叉策略为[9]

(18)

分别采取均匀变异策略和非均匀变异策略为[10]

(19)

(20)

Δ(g，y)=y×γ×(1-g/G)b

式中：b为形参，其值可取2～5，本算法中取2；γ为[0，1]的随机数，在计算过程中随机产生；G为终止代数，在本文算例中取200。

5 案例分析

5.1 初始数据设置

某城市轨道交通网络如图2所示，由3条线路构成，即R1，R2，R3。3条线路存在5个换乘车站a，b，c，d，e，其中R1与R2相交于换乘车站c，R1与R3相交于换乘车站b，d，R2与R3相交于换乘车站a，e。规定各线路运行时间如网络图中所示，例如线路R1中，由换乘站b出发到离开换乘站c的运行时间tbc=9.5 min，由换乘站c出发到离开换乘站d的运行时间tcd=7.3 min。为了计算方便，设定调整前相同两换乘站之间列车上行运行时间与下行运行时间相同。

图2 城市轨道交通网络

以10:00～12:00为例，设置换乘客流量见表1，单元格中的数据表示相交于对应换乘站的两线路所在行方向的一列车所带来的要换乘到所在列方向的客流量。

各线路上列车采取均衡行车方式， 且同一线路的上、下行行车间隔相同，R1、R2、R3行车间隔分别设置为h1=360 s，h2=330 s，h3=300 s。各车站各方向乘客换乘走行时间均设置为100 s。各换乘站对应线路上列车的停车时间设置见表2。

表1 每列车运送的换乘客流量数据 人

表2 各换乘站停站时间 s

根据图2线路网络所示，各线路上、下行方向在换乘站的离站时刻共有20个，因此，决策变量个数为20，采用实数编码方式的染色体设置见表3。

表3 实数编码染色体设置

每一代的种群规模设置为200，交叉概率取0.9，变异概率取0.1[11]。分别采取均匀变异策略和非均匀变异策略以验证计算结果。

5.2 计算结果及分析

通过均匀变异和非均匀变异两种方法计算，求得Pareto解集近似相同，图3显示了非均匀变异的计算结果。

图3 非均匀变异运算结果

图3显示的计算结果均为优化解，根据图3所示， 模型的两个目标存在“此消彼长”的博弈。若增大站间

运行时间的调整幅度，即目标f2增大，则乘客的换乘等待时间f1减小；相反，若目标f2减小，则目标f1增大。表4列出了两组调整方案，分别对应以上两种情况。

具体选择哪一组结果做调整方案，则由决策者根据以下情况判断：若期望调整对单线路的原有时刻表影响较小，即换乘站间列车运行时间调整幅度较小，则选择图3中偏右下方的优化解，例如表4中第1组优化解；而若更看重网络乘客的整体换乘时间优化，则选择图3中偏左上方的优化解，例如表4中第2组优化解。

为了检验优化效果，将模型的目标1网络乘客换乘总等待时间修改为取倒数后再求最小值，目标2不变，仍采用本文算法求解，对计算结果的目标1再取倒数变换后，由此得出一些站间运行时间调整幅度近似情况下的较劣运行时刻协调结果。表5列出了其中的一组较劣解，该组解与表4中的第1组解对比，全网换乘等待时间延长了约6.4%，与表4中的第2组解对比，换乘时间延长了约11.3%。

表4 两组优化解

表5 一组较劣解

6 结束语

本文分析了网络化运营条件下，线路间列车运行协调优化问题。针对平峰时段，以网络中乘客总换乘候车时间最少及路网列车运行参数调整幅度最小为目标建立多目标优化模型。设计了NSGA-Ⅱ算法，并对案例求解，结果验证了本模型能够有效减少乘客的换乘等待时间。研究过程及结论可为网络化的运行协调工作提供参考。

参考文献：

[1]张铭,杜世敏.基于递阶偏好的轨道交通网络化运营换乘协调优化[J].铁道学报,2009,31(6):9-14.

ZHANG Ming,DU Shimin.Transfer Coordination Optimization for Network Operation of Urban Rail Transit Based on Hierarchical Preference[J].Journal of the China Railway Society,2009,31(6):9-14.

[2]周艳芳,周磊山,乐逸祥.城市轨道网络换乘站列车衔接同步协调优化研究[J].铁道学报,2011,33(3):9-16.

ZHOU Yanfang,ZHOU Leishan,YUE Yixiang.Synchronized and Coordinated Train Connection Optimization for Transfer Stations of Urban Rail Networks[J].Journal of the China Railway Society,2011,33(3):9-16.

[3]徐瑞华,张铭,江志彬.基于线网运营协调的城市轨道交通首末班列车发车时间域研究[J].铁道学报,2008,30(2):7-11.

XU Ruihua,ZHANG Ming,JIANG Zhibin.Study on Departure Time Domain of the First and Last Trains of Urban Mass Transit Network Based on Operation Coordination[J].Journal of the China Railway Society,2008,30(2):7-11.

[4] RACHEL C W.Optimizing Timetable Synchronization for Rail Mass Transit[J].Transportation Science,2008,42(1):57-69.

[5] CUUNG M K,CHANG C S.Timetable Synchronization of Mass Rapid Transit System Using Multiobjective Evolutionary Approach[J].IEEE Transactions on Systems,Man,and Cybernetics,2008,38(5):636-648.

[6]孙鹏,赵佳虹,丁宏飞.基于换乘协调的城市轨道交通列车开行方案优化[J].铁道运输与经济,2011,33(12):67-70.

SUN Peng,ZHAO Jiahong,DING Hongfei.The Optimization of Urban Rail Transit Operation Scheme based on Coordinated Transfer[J].Railway Transport and Economy,2011,33(12):67-70.

[7]白广争,郭进,石红国,等.基于离站时刻协调的地铁换乘站列车衔接优化研究[J].交通运输系统工程与信息,2013,13(5):134-139,201.

BAI Guangzheng,GUO Jin,SHI Hongguo,et al.Optimization of Convergence Based on the Coordination of Train Departure Time in Transfer Station[J].Journal of Transportation Systems Engineering and Information Technology,2013,13(5):134-139,201.

[8]雷德明,严新平.多目标智能优化算法及其应用[M].北京:科学出版社,2009.

[9]陈小平,于盛林.实数遗传算法的交叉策略的改进[J].电子学报,2003(1):71-74.

CHEN Xiaoping,YU Shenglin.Improvement on Crossover Strategy of Real-valued Genetic Algorithm[J].Acta Electronica Sinica,2003(1):71-74.

[10]朱灿.实数编码遗传算法机理分析及算法改进研究[D].长沙：中南大学,2009.

[11]徐宗本.计算智能(第一册)——模拟进化算法[M].北京:高等教育出版社,2005.