基于扩展磁链的永磁同步牵引电机失磁在线监测
2016-05-07罗意平张昌凡赵凯辉
黄 刚,罗意平,张昌凡,赵凯辉
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.湖南工业大学 电气与信息工程学院,湖南 株洲 412007)
永磁同步电机以其优异性能和固有特点能够满足轨道车辆对动力品质、能耗和控制特性的要求[1-3]。德、法、日等国家已经相继研制出永磁同步电机的牵引传动系统,我国株洲南车时代电气股份有限公司也已完成了地铁车辆永磁同步牵引系统的研制并在沈阳地铁二号线进行了装车试验。永磁同步牵引系统已成为轨道交通牵引传动的未来发展方向[4,5]。然而由于我国幅员辽阔,列车运行跨度大,永磁同步牵引电机易受外部磁场环境和温度变化的影响导致永磁体失磁风险,这将直接导致电机发热和转矩性能变差,甚至造成电机报废,严重影响列车的安全运行[6,7]。因此针对永磁同步牵引电机的失磁进行预防,降低发生失磁的风险,具有重要的意义。
针对永磁同步电机的失磁和磁性能波动问题,国内外许多专家学者进行了广泛深入地研究。文献[8]针对不同工作状态的磁体在交变磁场作用下表面磁感应强度随时间的变化进行了研究,这是从优化磁路结构的电机设计角度出发去降低失磁风险的静态预防方法。文献[9]针对90 kW车用永磁牵引电机,利用有限元仿真方法对永磁体工作点进行了检测,这是一种发生失磁后的离线检测,此时电机很可能已经损坏。因此采用适用的现代控制理论对失磁故障进行在线检测是十分有必要的。文献[10]提出一种单相永磁同步电机不可逆失磁状况的预估方法,但需要知道电机的定转子结构和永磁体的材料特性。文献[11]把改进的反电势方法用于永磁体磁链的在线估计,但只能估计固定方向磁链幅值的波动。文献[12] 针对隐极式永磁同步电机提出了基于卡尔曼滤波器的永磁体磁场在线监测方法,但由于卡尔曼滤波器在实际应用中存在建模误差及模型线性化和离散化过程中的量化误差,限制了其实际工程应用。文献[13]提出一种基于双观测器的内置式永磁同步电机失磁故障检测方法,但其是在速度闭环控制且负载转矩小的情况下实现的,不能直接应用到转矩闭环的大负载转矩的牵引传动系统中去。
本文针对内置式永磁同步电机转矩闭环控制系统,结合对系统参数摄动、外界扰动及数学模型不准确具有很好鲁棒性的滑模变结构控制方法[14,15],设计了一种基于扩展磁链的滑模观测器,用于对永磁同步电机转矩闭环控制系统的反馈转矩和永磁体磁链进行在线计算和检测。仿真结果表明,该观测器可准确在线动态检测转子磁链信息和反馈转矩,具有较高的观测精度。结合RT-LAB和真实的DSP电机控制器搭建硬件在环仿真试验系统,通过试验验证了所提方法的有效性和实时性。
1 PMSM数学模型
按转子磁链定向的dq坐标系下PMSM数学模型可描述为
( 1 )
dq坐标系中的磁链方程为
( 2 )
式中:Rs为定子绕组电阻;Ld、Lq分别为定子绕组的d、q轴电感;ud、uq分别为定子绕组的d、q轴电压;id、iq分别为定子绕组的d、q轴电流;Ψr为转子永磁体磁链;Ψd、Ψq分别为定子绕组的d、q轴磁链分量;ω为转子电角速度;np为转子磁极对数;D为微分算子。
当永磁电机由于种种原因发生永磁体失磁故障时,永磁体磁链幅值和方向发生变化,如图1所示。

图1 内置式永磁同步电机永磁体磁链的变化
dq坐标系中的磁链方程变为
( 3 )
式中:Ψrd、Ψrq分别为永磁体磁链在dq坐标系下产生的新的磁链分量。
把式( 3 )代入式( 1 ),并考虑实际系统中DΨrd≈0、DΨrq≈0,可得发生永磁体失磁故障时的dq坐标系下电压方程为
( 4 )
由式( 1 )进行坐标逆变换得其在αβ坐标系下电压方程为
( 5 )
式中:L1=(Ld+Lq)/2;L2=(Ld-Lq)/2;uα、uβ分别为定子绕组的α、β轴电压;iα、iβ分别为定子绕组的α、β轴电流;Ψr为转子永磁体磁链;θ为转子电角度。式中带有2θ的项显示了内置式永磁同步电机的凸极特性,对永磁同步电机的观测产生了诸多不便。
为了克服内置式永磁同步电机的凸极特性对磁链观测的不利影响,对发生永磁体失磁故障时的dq坐标系下电压方程式( 4 )进行重构。

( 6 )
式( 6 )中,第2项即为dq坐标系下的扩展磁链项,且电压方程中的电感矩阵为对称矩阵,仅包含Rs和Lq。对式( 6 )进行坐标逆变换,可求得发生永磁体失磁故障时αβ坐标系下的定子电压方程为
( 7 )

( 8 )
可得
uαβ=Rsiαβ+DLqiαβ+DΨαβ
( 9 )
并有
DΨαβ=ωJΨαβ
(10)
其电磁转矩表达式为
(11)

2 滑模状态观测器设计及转矩和永磁体失磁磁链重构
根据式( 9 )和式(10)构建以扩展磁链为状态变量的状态空间表达式[16]。
(12)
式中:y为输出向量。构建扩展磁链滑模状态观测器。
(13)

=-ωe2-k1|e1|sgn(e1)
(14)
=ωe1-k2|e2|sgn(e2)
(15)
选取适当的k1和k2,可保证式(14)和式(15)确定的观测器误差方程收敛到零。
证明:选取Lyapunov函数为
(16)
对式(16)求导并代入式(14)和式(15),可得
(17)
根据Lyapunov稳定性理论,所设计的滑模观测器渐进稳定。据此,系统状态达到滑模面后有e=0,可得
(18)
对式(18)进行移项整理并进行积分可得基于定子电压模型的定子磁链观测值为
(19)
将式(19)代入式(11)可得转矩的观测值为
(20)
尽管扩展磁链的观测会受到交轴电感的影响,但研究发现通过本文方案观测到的定子磁链却不受交直轴电感的影响,式(19)获得的定子磁链既保留了电压模型法计算定子磁链的参数鲁棒性,又克服了直接电压模型的纯积分问题。即由式(20)确定的转矩观测值也不受交直轴电感的影响,进而确保了转矩观测的准确性[16]。常规的转矩控制方式是根据PMSM在同步旋转坐标系下电磁转矩公式开环计算出电流指令,并通过电流闭环控制实现对电流指令的跟踪。这种方法需要用到转子永磁体磁链等电机参数,而这些参数的变化会造成依据所接收到的转矩指令计算出的电流指令偏离实际需要值,难以保证转矩控制精度。而由式(20)确定的转矩观测式不包含永磁体磁链等信息,因此本文转矩观测亦不受转子磁链变化的影响。
由系统状态达到滑模面后和e=0式( 8 )可得发生失磁故障时等效的转子永磁体磁链dq轴分量为
(21)
3 仿真与分析
综合以上分析和设计,基于扩展磁链的内置式永磁同步电机转矩闭环控制系统如图2所示。

图2 基于扩展磁链滑模观测器的转矩闭环控制

仿真所用内置式永磁同步电机参数见表1。为了减少滑模的抖动,仿真时采用连续函数代替符号函数sgn(·)。

表1 内置式永磁同步电机参数
因牵引电机运行中实际失磁动态变化过程很难模拟,所以仿真系统中采取设置磁链幅值初始值偏差和位置偏差的方法来模拟永磁体磁链幅值和方向的变化,这两种情况下磁链观测过程是一样的,所以可以用来验证本方法的有效性。
为验证所设计观测器的鲁棒性,设置转速初始值为200 rad/s,0.1 s增加为400 rad/s;定子电阻初始值为0.02 Ω,在0.2 s增加为0.04 Ω;转矩给定为500 Nm,在0.3 s时增加为1 000 Nm。分3种情况进行讨论。
3.1 无失磁时
仿真结果如图3~图7所示。

图3 定子d、q轴电流

图4 转矩给定值、实际值、观测值及观测误差

图5 扩展磁链观测值

图6 d轴转子磁链的实际值、观测值及观测误差

图7 q轴转子磁链的实际值、观测值及观测误差
图3为定子d、q轴电流波形,在0.3 s由于转矩增大,q轴电流变大,d轴电流跳变后迅速恢复到零;图4为转矩给定值、实际值、观测值及观测误差波形;图5为扩展磁链观测值波形,由于在0.1 s转速变大而使电角速度频率变大;图6和图7分别为d、q轴转子磁链的实际值、观测值及观测误差波形。从图中波形可知,转矩及永磁体磁链的观测对定子电阻、转速及转矩等参数变化不敏感,系统鲁棒性强,转矩及转子d、q轴磁链观测值可以迅速跟踪其给定值或实际值,观测精度高。
3.2 发生幅值失磁时
其他条件不变,假设在0.4 s时,转子磁链幅值由0.892 Wb变为0.7 Wb。仿真结果如图8~图12所示。

图8 定子d、q轴电流

图9 转矩给定值、实际值、观测值及观测误差

图10 扩展磁链观测值

图11 d轴转子磁链的实际值、观测值及观测误差

图12 q轴转子磁链的实际值、观测值及观测误差
图8为定子d、q轴电流波形,从图8可知定子q轴电流由于在0.4 s发生幅值失磁而变大;图9为转矩给定值、实际值、观测值及观测误差波形,刚发生幅值失磁时观测值有波动,但能很快跟踪给定值;图10为扩展磁链观测值波形,由于在0.4 s发生幅值失磁而变小;图11和图12分别为d、q轴转子磁链的实际值、观测值及观测误差波形,幅值失磁导致磁链d轴分量减小,q轴分量不变,磁链观测值可以迅速跟踪相应的实际值。
3.3 同时发生幅值失磁和角度失磁时
其他条件不变,为方便观察,假设在0.4 s时,转子磁链幅值由0.892 Wb变为0.7 Wb,在0.45 s时,转子磁链位置偏差由0°变为30°。图13为定子d、q轴电流波形,从图13可知在发生幅值失磁和角度失磁时,定子q轴电流均变大;图14为转矩给定值、实际值、观测值及观测误差波形,在刚发生失磁时观测值有小的波动,但亦能迅速跟踪给定值;图15为扩展磁链观测值波形,从波形可知由于幅值失磁导致扩展磁链变小,而角度失磁对扩展磁链的大小没有影响;图16和图17分别为d、q轴转子磁链的实际值、观测值及观测误差波形,从图中可知磁链观测值能迅速跟踪相应的实际值。

图13 定子d、q轴电流
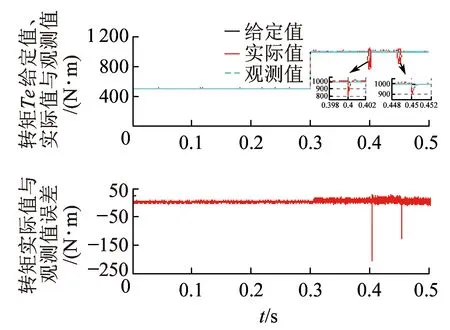
图14 转矩给定值、实际值、观测值及观测误差

图15 扩展磁链观测值

图16 d轴转子磁链的实际值、观测值及观测误差

图17 q轴转子磁链的实际值、观测值及观测误差
通过仿真及分析充分验证了所设计的基于扩展磁链的自适应滑模观测器的跟踪性能优良,观测精度高,对系统参数变化具有鲁棒性。
4 硬件在环试验及结果
为了验证所设计的在线监测方法,搭建RT-LAB硬件在环仿真测试系统。RT-LAB是由加拿大Opal-RT公司开发的一套模块化的实时仿真平台,可以直接应用MATLAB建立的动态数学模型应用于实时仿真、控制、测试及其他相关领域。图18为永磁同步电机控制系统RT-LAB硬件在环配置图。包括DSP控制器TMS320F2812以及RT-LAB OP5600实时仿真模型(逆变器和永磁同步电机)。将控制对象永磁同步电机及逆变器模型编译下载到OP5600中,并将设计的控制器模型生成C代码下载到DSP控制器中,通过采集电机电流和位置等模拟输出信号,并将模拟信号转换为±10 V范围内的信号,采集实时模型输出转换后的信号并完成相应的控制算法后,输出6路PWM脉冲给实时仿真模型,即可实现永磁同步电机控制的硬件在环仿真。仿真中PWM载波频率设为5 kHz,采样周期设为20 μs,电机参数设定同表1。

图18 RT-LAB硬件在环系统
图19和图20为无失磁情况下定子d、q轴实际电流、转矩实际值及观测值和d、q轴转子磁链观测值;图21和图22为幅值失磁情况下定子d、q轴实际电流、转矩实际值及观测值和d、q轴转子磁链观测值;图23和图24为幅值和角度均失磁情况下定子d、q轴实际电流、转矩实际值及观测值和d、q轴转子磁链观测值。

图19 定子d、q轴电流及转矩实际值和观测值(电流:150 A/div;转矩:500 Nm/div;t:250 ms/div)

图20 d、q轴转子磁链观测值(磁链:0.5 Wb/div;t:250 ms/div)

图21 定子d、q轴电流及转矩实际值和观测值(电流:150 A/div;转矩:500 Nm/div;t:250 ms/div)

图22 d、q轴转子磁链观测值(磁链:0.5 Wb/div;t:250 ms/div)

图23 定子d、q轴电流及转矩实际值和观测值(电流:150 A/div;转矩:500 Nm/div;t:250 ms/div)

图24 d、q轴转子磁链观测值(磁链:0.5 Wb/div;t:250 ms/div)
通过对比不同情况下的仿真结果和试验波形,两者波形基本相似,试验结果证明了所设计观测器能够准确辨识永磁体的磁链,系统动态性能较好,实时性较高。
5 结论
本文提出一种基于扩展磁链的变速趋近律滑模观测器的转矩闭环内置式永磁同步牵引电机控制系统转矩和永磁体失磁在线监测方法。建立两相静止坐标系下基于扩展磁链的内置式永磁同步牵引电机失磁故障的数学模型,通过选择扩展磁链为状态变量,构建了估算转矩和永磁体磁链的变速趋近律滑模观测器。该方法所设计的观测器结构简单,理论推导和稳定性证明简单,对电机参数依赖较少。通过RT-LAB搭建的硬件在环实时仿真系统进行试验,其试验结果和MATLAB仿真结果均显示系统动态响应速度更快,动态过程超调更小,具有更好的系统动态性能,能以更快的速度跟踪变化量,对转矩变化和永磁体磁链能够进行精确观测辨识,且转矩观测不受交直轴电感和转子磁链变化的影响,具有较强的鲁棒性,验证了所提方法的准确性和有效性。本文方法可为转矩闭环永磁同步牵引电机控制系统提供准确的转矩反馈和永磁体磁链信息,有利于提高永磁同步电机牵引传动系统的控制性能和预防不可逆失磁风险,对于轨道列车的安全运行具有重要的意义。
参考文献:
[1]冯江华,桂卫华,符敏利,等.铁道车辆牵引系统用永磁同步电机比较[J].铁道学报,2007,29(5):111-116.
FENG Jianghua,GUI Weihua,FU Minli,et al.Comparison of Permanent Magnet Synchronous Motors Applied to Railway Vehicle Traction System[J].Journal of the China Railway Society,2007,29(5):111-116.
[2]Matsuoka Koichi.Development Trend of the Permanent Magnet Synchronous Motor for Railway Traction[J].IEEJ Transactions on Electrical and Electronic Engineering,2007,2(2):154-161.
[3]盛义发,喻寿益,桂卫华,等.轨道车辆用永磁同步电机系统弱磁控制策略[J].中国电机工程学报,2010,30(9):74-79.
SHENG Yifa,YU Shouyi,GUI Weihua,et al.Field Weakening Operation Control Strategies of Permanent Magnet Synchronous Motor for Railway Vehicle[J].Proceedings of the CSEE,2010,30(9):74-79.
[4]许俊峰,李耘茏,许建平.永磁同步电机作为机车牵引电机的应用现状及前景[J].铁道学报,2005,27(2):130-132.
XU Junfeng,LI Yunlong,XU Jianping.Present Situation and Prospect of Applying Permanent Magnet Synchronous Motors to Railway Locomotives[J].Journal of the China Railway Society,2005,27(2):130-132.
[5]冯江华.轨道交通永磁同步牵引系统的发展概况及应用挑战[J].大功率变流技术,2012(3):1-7.
FENG Jianghua.Development Overview and Application Challenges of Permanent Magnet Synchronous Traction System for Rail Transit[J].High Power Converter Technology,2012(3):1-7.
[6]唐任远.稀土永磁电机的关键技术与高性能电机开发[J].沈阳工业大学学报,2005,27(2):162-166.
TANG Renyuan.Research and Development of Rare-earth Permanent Magnet Machines[J].Journal of Shen yang University of Technology,2005,27(2):162-166.
[7]Krishnan R,Praveen Vijayraghavan.Fast Estimation and Compensation of Rotor Flux Linkage in Permanent Magnet Synchronous Machines[C]//IEEE ISIE,Bled,Slovenia,1999.
[8]黄浩,柴建云,姜忠良,等.汝铁硼稀土永磁材料交流失磁[J].清华大学学报,2004,44(6):721-724.
HUANG Hao,CHAI Jianyun,JIANG Zhongliang,et al.Excitation Loss in a Nd-Fe-B Magnetic Materials with Alternating Magnetic Fields[J].Journal of Tsinghua University,2004,44(6):721-724.
[9]陈致初,符敏利,彭俊.永磁牵引电动机的失磁故障分析及预防措施[J].大功率变流技术,2010(3):42-45.
CHEN Zhichu,FU Minli,PENG Jun.Demagnetization Analysis and Preventive Measures of Permanent Magnet Traction Motor[J].High Power Converter Technology,2010(3):42-45.
[10]Kang Gyuhong,Jin Hur,Hyuk Nam,et al.Analysis of Irreversible Magnet Demagnetization in Line-start Motors Based on the Finite-element Method[J].IEEE Transactions on Magnetics,2003,39(3):1 488-1 491.
[11]CHEN Zhiqian,Tomita Mutuwo,Doki Shinji,et al.An Extended Electromotive Force Model for Sensorless Control of Interior Permanent-magnet Synchronous Motors[J].IEEE Transactions on Industrial Electronics,2003,50(2):288-295.
[12]肖曦,张猛,李永东.永磁同步电机永磁体状况在线监测[J].中国电机工程学报,2007,27(24):43-47.
XIAO Xi,ZHANG Meng,LI Yongdong.On-line Estimation of Permanent-magnet Flux Linkage Ripple for PMSM[J].Proceedings of the CSEE,2007,27(24):43-47.
[13]何静,张昌凡,贾林,等.一种永磁同步电机的失磁故障重构方法研究[J].电机与控制学报,2014,18(2):8-14.
HE Jing,ZHANG Changfan,JIA Lin,et al.Demagnetization Fault Reconstruction for Permanent Magnet Synchronous Motor[J].Electric Machines and Control,2014,18(2):8-14.
[14]张昌凡,王耀南,何静.永磁同步伺服电机的变结构智能控制[J].中国电机工程学报,2002,22(7):13-17.
ZHANG Changfan,WANG Yaonan,HE Jing.Variable Structure Intelligent Control for PM Synchronous Servo Motor Drive[J].Proceedings of the CSEE,2002,22(7):13-17.
[15]TAN C P,EDWARDS C.Sliding Mode Observers for Detection and Reconstruction of Sensor Faults[J].Automatica,2002,38:1 815-1 821.
[16]杨淑英,占琦,张兴,等.基于扩展磁链观测的永磁同步电机转矩闭环矢量控制[J].电力系统自动化,2014,38(6):80-84.
YANG Shuying,ZHAN Qi,ZHANG Xing,et al.Torque Closed-loop Vector Control Based on Extended Flux Linkage Observer of Permanent Magnet Synchronous Motor[J].Automation of Electric Power Systems,2014,38(6):80-84.
