高速列车静态升降弓时弓网电弧稳态特性仿真与分析
2016-05-07朱光亚吴广宁韩伟峰高国强刘贤汭
朱光亚,吴广宁,韩伟峰,高国强,刘贤汭
(西南交通大学 电气工程学院,四川 成都 610031)
高速列车起动过程中,由于静态升降弓造成弓网离线,此时,接触网导线和受电弓滑板之间的离线电压高,列车起动电流大,导致离线间隙间的空气发生击穿,产生大量的电子、离子,并最终使得间隙的空气呈现离子态,产生弓网电弧。电弧的存在一方面对于维系弓网系统在离线过程中的持续受流有很重要的作用,另一方面,电弧燃烧过程中的弧柱最高温度超过10 000 K,接触线表面和滑板表面温度极高,导致接触线表面的金属熔溅,碳滑板表面也出现“麻点”,弓网接触面材料严重磨损[1,2],如图1所示。因此,开展弓网电弧燃烧过程温度场分布的研究,分析弓网系统几何参数及列车运行电气参数对电弧温度场分布的影响,并最终得出接触副材料的电气磨损机理,对于提升弓网系统的服役性能,保障高速铁路弓网系统的安全、稳定,保障列车可靠运行有着重要的现实意义。

图1 现场运行弓网接触面磨损情况
目前,国内外有关弓网电弧的研究主要是关于电弧产生过程中的电压、电流等电气参数的变化特性,电弧温度场分布及电弧形态变化等内容的研究则主要集中于开关电弧和真空电弧,对于弓网电弧温度分布和形态变化的研究较少。文献[3-5]采用净发射系数法(NEC)分析开关电弧弧柱的温度场分布。西安交通大学吴翊利用P1辐射模型仿真分析开关电弧的温度分布,指出在仿真分析电弧燃烧过程中温度分布情况时,不仅要考虑电弧高温部分对外界辐射的能量,还要考虑电弧边界低温区域对辐射能量的吸收,并指出采用P1辐射模型模拟电弧温度场分布更可靠。针对大电流真空电弧,西安交通大学王立军根据不同的离子运动状态以及阴极斑点分布,耦合求解流体方程和电磁以及电子能量方程,建立了真空电弧磁流体动力学仿真模型。
作为维持高速列车弓网受流的一种特殊的能量传输方式,弓网电弧与开关电弧和真空电弧不同,弓网系统离线电弧产生后,由于电弧对于维持弓网离线过程中的持续受流有很重要的作用,因此不能像开关电弧一样及时灭弧。同时,开关电弧处于相对密闭的灭弧室内,而弓网电弧处于列车运行过程所产生的强大气流场环境中。真空电弧的产生主要是由电极材料的蒸发和熔溅,金属蒸气电离产生金属离子,而弓网电弧主要是由于弓网间隙气体的电离击穿。随着我国高速列车运行速度的提高,亟待深入开展弓网电弧的特性研究,分析电弧等离子体的温度场等能量分布,并最终提高弓网系统的服役性能。然而,综合考虑列车运行过程中的各种因素,分析不同车速、弓网电流等情况时的电弧特性变化规律是一个复杂的物理建模过程,因此,本文就高速列车静态升降弓时的电弧特性变化情况进行分析,为后续开展相应工作奠定基础。
1 弓网电弧模型建立
1.1 列车现场运行过程静态升降弓时电弧的产生
静态升降弓时的弓网电弧燃弧过程分为接触燃弧和分断燃弧两种。列车弓网运行原理图如图2所示。

图2 弓网运行原理图
图中,1表示接触网导线,2表示受电弓滑板,3表示受电弓,弓网系统部分的阴影区域表示弓网电弧。如图2所示接线情况,当列车起动时,受电弓先升弓,然后闭合主断路器。在该过程中,弓网从分离到接触时,弓网间隙的电场强度增加,场电子发生雪崩现象,电弧中的电流强度增强,接触燃弧剧烈。列车制动时,先断开主断路器,再降弓。在该过程中,弓网从接触到分离时,电极温度高,在温度场和电场联合作用下,弓网间隙被击穿,形成电弧。
1.2 模型假设
由以上分析可知,实际的高速铁路弓网离线电弧物理化学过程较复杂,为了分析电弧的能量分布等特性,对弓网电弧模型做以下假设:
(1)弓网电弧等离子体区域处于局部热力学平衡状态,且忽略电弧等离子体的重力影响。
(2)电弧等离子体的物性参数随温度变化,忽略压力等其他参数对物性参数的影响。
(3)忽略滑板材料的焦耳热,即不考虑滑板及接触线中电流所产生的焦耳热对其内部温度场分布的影响。
(4)在电弧发生过程中,忽略电极材料的相变对温度场分布的影响。
1.3 弓网系统几何模型的建立
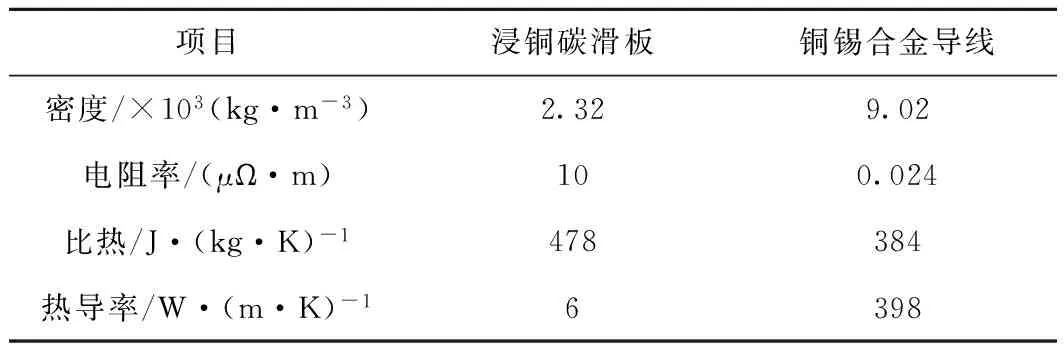
沿着接触网导线方向建立弓网系统二维几何模型,如图3所示。图中,接触线、滑板形态和尺寸与实际运行弓网系统一致。接触线弧形轮廓半径为6.5 mm,d表示弓网离线距离。在本文仿真计算过程中,将d值设置为4 mm。接触网导线为铜锡合金导线,受电弓滑板为浸铜碳滑板,其物性参数见表1。求解域内空气的物性参数随温度不断变化。

图3 弓网系统几何模型
项目浸铜碳滑板铜锡合金导线密度/×103(kg·m-3)2.329.02电阻率/(μΩ·m)100.024比热/J·(kg·K)-1478384热导率/W·(m·K)-16398
1.4 弓网电弧磁流体动力学(MHD)模型及多场耦合
弓网离线后,弓网电弧持续稳定燃烧过程中,电弧热场、电磁场以及外界环境气流场耦合并相互作用,如图4所示。各场通过相关参数的互相影响而相互耦合。弓网电弧等离子体的物性参数包括密度、黏性系数、比热、电导率和热导率。随着温度的不断变化,物性参数会不断变化。因此,在电弧燃烧过程中,随着电弧温度的不断变化,等离子体的电导率发生变化,导致电弧电场和电流的变化,电磁场发生改变。同时,由电流密度产生的单位体积焦耳热将会作为源项,直接参与电弧能量方程的计算。磁场作用下的洛伦兹力将与电弧周围气流场相互耦合,作为体积力参与电弧动量方程的计算。在列车运行过程中,强烈的走行风会导致电弧周围气流场的变化,对于电弧等离子体有冷却吹弧的效果,并导致电弧物性参数的变化。因此,在整个弓网电弧仿真过程中,各个物理场方程组的计算均通过相关参数直接或间接的耦合。

图4 弓网电弧多场耦合
弓网电弧MHD模型的建立,是在简化弓网系统几何模型的基础上,耦合各个物理场,通过求解场域方程组,得出模型的温度场分布情况,并对电弧温度场及接触网导线和受电弓滑板内部的温度分布情况进行分析,研究电弧稳态燃烧时,电流大小对弓网系统电气磨损的影响。
(1)流体动力学方程
本文采用Ansys软件的Fluent软件包建立弓网电弧MHD模型。然而,Fluent软件包只能仿真分析传统流体,而电弧等离子体是一种特殊的流体,因此需要对其进行二次开发。流体流动要受物理守恒定律的支配,基本守恒方程包括:质量守恒方程、动量守恒方程和能量守恒方程。
( 1 )
( 2 )
( 3 )
式中:ρ为等离子体密度;v是速度矢量;vi为不同方向的速度分量;η为黏性系数;p为压强;T为温度;λ为热导率;cp为比热容。Svi作为流体的动量源项,是磁场作用下电弧受到的洛伦兹力,该磁场包括电弧电流所产生的感应磁场,以及接触导线中的电流所产生的磁场。ST是电弧的能量源项,包括流体的黏性耗散、焦耳热以及电弧高温区域向外辐射的能量部分。
Svi=J×(B0+Bi)
( 4 )
( 5 )
式中:J是电弧电流密度;B0和Bi分别是电弧自身电流和接触网导线电流在电弧区域产生磁场的强度;V是黏性耗散项;σ是等离子体电导率;J2/σ是电弧电流产生的焦耳热;QR是电弧经热辐射的净耗散能量。
(2)电磁场方程
根据麦克斯韦方程组,电场φ的计算方程为
div(σgradφ)=0
( 6 )
电流密度为
j=-σgradφ
( 7 )
弓网电弧稳态燃烧过程中,弓网系统持续受流,接触网导线中的时变电流将在其周围区域产生磁场。将导线等效为一根半无限长导线,用毕奥-萨伐定律求解磁感应强度。
( 8 )
式中:i为接触网导线中的电流;μ为等离子体的磁导率;r为距接触网导线的垂直距离。
(3)电弧能量辐射
在电弧稳定燃烧过程中,电弧弧柱内部最高温度超过10 000 K,此时,辐射成为最重要的能量耗散方式[6]。因此,在仿真计算电弧温度场分布的过程中,考虑电弧等离子体的辐射能量耗散具有重要的意义。根据Stefan-Boltzman公式,电弧燃烧时的辐射量为
( 9 )
式中:α为Stefan-Boltzman常数,约为5.670 57×10-8W/(m2·K);K为吸收系数,与网格单元内的压强有关;T为网格单元内的温度;T0为外部环境温度。
1.5 模型边界条件设置
(1)热边界条件设置
为了求解电弧模型的温度场分布,必须对几何模型边界设置热边界条件。在电弧燃烧的过程中,电弧等离子体与电极表面温度存在极大的温度差,电弧弧根与电极表面的交界面处存在强烈的热传导过程,导致一部分电弧能量传导至接触网导线表面和受电弓滑板表面。根据Fluent软件的计算特点,在两电极表面处施加温度边界条件,并利用耦合求解算法,用一维热传导计算公式得出接触线和滑板的温度分布情况。
(2)电场边界条件
在电弧阴极-等离子体界面处,通过施加电流密度边界条件求解方程组。对于弓网电弧,实际的电流密度分布情况很难准确得到,所以在仿真过程中多采用假定的电流密度来计算。文献[7-9]认为,电流通道主要位于电弧等离子体的高温区域,电流密度的分布情况与电极的温度和电弧弧柱的电导率相关,因此,电流密度的分布可以用于稳态和暂态计算,且计算结果可以用于描述实际电弧的运动。
当在电极处施加电流密度I时,电流会被“划分”到每个边界元Ai,因此电流密度分布为

对于阳极-电弧等离子体界面处的边界,施加零电势边界条件。为了考虑电弧等离子体区域对阳极斑点的传热进行分析,将界面处设置为耦合界面,热边界条件设置为耦合传热边界条件。
2 仿真结果及讨论
研究表明,静态弓网电弧对接触面的烧蚀最为严重[10],接触网断线事故也多发生在站场和电力机务段内[11]。在列车启动时,弓网系统处于静态升降弓状态,起动电流大,外界气流场作用小,可以忽略。为了分析列车启动过程中弓网系统静态升降弓时的电气烧蚀情况,本文建立弓网电弧的MHD模型,仿真分析电弧的温度场分布以及接触线导线和受电弓滑板内部的温度分布情况。
2.1 初始情况电弧温度分布
初始时,设定电弧电流为100 A,得出弓网系统的温度场分布如图5所示。

(a)电弧弧柱温度分布

(b)电弧弧柱轴向温度分布曲线图

(c)接触网导线的温度分布

(d)受电弓滑板的温度分布图5 100 A时电弧温度分布图
由图5(a)可知,电弧弧柱轴心温度高于10 000 K,弧柱最高温度可以达到15 000 K,同时,靠近接触线导线表面的弧柱半径趋于压缩。在图5(a)电弧弧柱温度分布图中,取如图所示AB线上的温度数据,做电弧弧柱轴向温度分布曲线,如图5(b)所示。可以看出,电弧弧柱最高温度位于弧柱靠近接触线的部分,但是在出现最高温度点后,弧柱温度急剧下降。由图5(c)可知,弧柱到达接触线表面的最高温度约为1 500 K 左右。分析可知,接触线的主要材料为铜,在电弧稳定燃烧过程中,接触线表面的铜金属熔化变成铜蒸气,而铜蒸气的热导率高于空气的热导率。因此,铜蒸气的存在提高了电弧的热辐射量,导致靠近接触线表面的电弧弧柱出现一定的冷却。同时,铜蒸气的进入提高了接触线表面的电弧弧柱电导率,使得弧柱受到的径向洛伦兹力增加,致使弧柱收缩。图5(d)为受电弓滑板的温度分布情况,可以看出,滑板表面的最高温度已超过4 000 K。
2.2 不同电流大小情况下的电弧温度分布
本文仿真分析在弓网系统静态升降弓过程中,不同弓网电流情况下的电弧温度场分布情况。当电弧电流值为200 A时,弓网系统的温度场分布情况如图6所示。

(a)电弧弧柱温度分布

(b)接触网导线的温度分布

(c)受电弓滑板的温度分布图6 200 A时电弧温度分布图
当设置电弧电流值为300 A时,仿真得出弓网系统的温度分布如图7所示。

(a)电弧弧柱温度分布

(b)接触网导线的温度分布

(c)受电弓滑板的温度分布图7 300 A时电弧温度分布图
分析在100 A、200 A、300 A时的电弧温度分布,得出弓网系统各个部分最高温度值,见表2。

表2 不同电流时弓网系统的最高温度 K
由表2可以看出,随着弓网电流的不断增大,电弧弧柱的最高温度变化不大,但接触线表面和滑板表面的温度不断升高。结合仿真结果图分析可知,电弧电流增大对于弧柱中心温度值影响较小,但弧柱半径会增大,且电弧弧柱区域对接触线和滑板的传导热量不断升高,最终导致弓网系统的电气磨损情况更加严重。比较接触线表面和滑板表面的最高温度值,随着电弧电流的升高,滑板表面最高温度值上升幅度更大,即使在静态升降弓时,受电弓滑板的电气磨损情况较接触网导线严重。同时,在列车运行过程中,电弧在接触线上的弧根会在列车运行方向上前进,而滑板上的弧根位置仍然在滑板上“之”字形跳变,另一方面,铜导线的导热率更高,电弧对接触线的热传导量会在导线内部迅速扩散。因此,滑板的电气磨损状况比接触线的磨损情况更严重。
3 仿真模型的验证
由于弓网电弧稳定燃烧时温度很高,且电弧持续时间短,想要通过试验手段测试电弧燃烧过程中的温度分布情况难以实现。为了验证本文仿真结果的正确性,试验测试了静态升降弓时电弧稳定燃烧的电气特性参数,得出电弧的电气特性如图8所示。仿真得出的电弧电位分布如图9所示。

图8 试验弓网电弧的电气特性

图9 仿真电弧电位分布图1—0.0 V;2—3.2 V;3—6.3 V;4—9.5 V;5—12.6 V;6—15.8 V;7—19.0 V;8—22.1 V;9—25.3 V;10—28.4 V。
图8所示红实线所圈选部分为电弧稳定燃烧时的电压变化情况。可以得出,电弧稳定燃烧时的电压大小基本不变,为23 V左右。由图9可知,接触网导线设置为零电势边界条件,故电位值为零。其他位置处的电势值如图9所示,电弧两端的电位差为28.4 V,仿真结果与实测结果之间有一定的差距。造成这个差值的原因,是由于本文在建立弓网电弧模型时,为了方便仿真求解计算,对模型进行了一定的假设。同时,在仿真施加边界条件时,与实际情况也存在一定的偏差,但这并不影响模型建立与仿真结果的正确性。
4 结论
本文利用有限元仿真软件建立弓网电弧物理模型,计算得出弓网系统静态升降弓时的电弧温度场分布及接触线和滑板内部的温度分布情况,同时分析了在不同电弧电流情况下弓网系统温度场分布的变化情况。研究表明,高速列车弓网系统的受电弓滑板电气磨损情况比接触网导线更严重。
参考文献:
[1]Shunichi Kubo,Koji Kato.Effect of Arc Discharge on Wear Rate of Cu-impregnated Carbon Strip in Unlubricated Sliding Against Cu Trollu under Electric Current[J].Wear,1998,216:172-178.
[2]Hiroki Nagasawa,Koji Kato.Wear Mechanism of Copper Alloy Wire Sliding Against Iron Base Strip under Electric Current[J].Wear,1998,216:179- 183.
[3]ZHU P,LOWKE J J,MORROW R.A Unified Theory of Free Burning Arcs,Cathode Sheaths and Cathodes[J].Journal of Physics D:Applied Physics,1992(25):1 221-1 230.
[4]LOWKE J J,KOVITYA P,SCHMIDT H P.Theory of Free Burning Arc Columns Including the Influence of the Cathode[J].Journal of Physics D:Applied Physics,1992(25):1 600-1 606.
[5]ZHANG J F,FANG M T,et al.Theoretical Investigation of a 2KA DC Nitriogen Arc in a Supersonic Nozzle[J].Journal of Physics D:Applied Physics,1987(20):366-379.
[6]王伟宗,等.空气开关电弧仿真技术及其应用的研究[J].低压电器,2010(5):7-10.
WANG Weizong,et al.Research of Simulation Technique of Electric Arc in Air Switch and Its Application[J].Low Voltage Apparatus,2010(5):7-10.
[7]KARETTA F,LINDMAYER M.Simulation of the Dynamic and Electromagnetic Processes in Low Voltage Switching Arcs[J].IEEE Fransations on Components,Packaging,and Manufacturing Technology,Part A,1998,21(1):96-103.
[8]LINDMAYER M.Complete Simulation of Moving Arc in Low-voltage Switchgear.Proc[C]//14thInt.Conf.on Gas Discharge and their Application(Livepool),2002,Vol.2:318-324.
[9]KARETTA F,LINDMAYER M.Simulation of Arc Motion between Divergent Arc Runners[C]//19thInternational Conference on Electriccontact Phenomena,1998.
[10]吴积钦,钱清泉.弓网系统电弧侵蚀接触线时的热分析[J].铁道学报,2008,30(3):31-34.
WU Jiqin,QIAN Qingquan.Thermal Analysis of Arc Erosion of Contact Wire of the Pantograph & Catenary System[J].Journal of the China Railway Society,2008,30(3):31-34.
[11]周自成.大秦线铜导线断线原因浅析[J].电气化铁道,2000(3):22-26.
ZHOU Zicheng.Analysis on Breakage of Copper Contact Wire on DaqinRailway[J].Electric Railway,2000(3):22-26.
