实验：数学教学中美丽的花朵

洪三球

1.问题的提出

江苏科学技术出版社编著的义务教育教科书，《数学》（九年级上册）4.1等可能性，有这样一道例题：

一只不透明的袋子中装有1个白球和2个红球，这些球除颜色外都相同，搅匀后从中任意摸出1个球，会出现哪些可能的结果？摸出白球与红球的可能性一样吗？

在强调让实验走进数学课堂的大背景下，如何准确处理这道例题才是恰当的呢？

2.问题的分析解决

2015年9月笔者参加了昆山及苏州大市的百节优秀课评比，课题恰好就是《等可能性》。随着比赛层次的提高，对这道例题的认识也在不断深化。

2.1片级初赛——对本例题进行了简单的解读和讲评。

由于初赛是在昆山市南片几所学校之间进行，笔者对这道例题并未做深入解读，在学习了等可能性的条件后，直接按等可能性的四条要点进行逐一分析：因为袋中有两个红球和一个白球，摸到红球的可能性要大一些，所以摸到白球与摸到红球不是等可能的。但是在课后反思中，笔者觉得在对这道例题的处理过程中过分强调了形式化的逻辑推导和形式化的结果，对数学发现过程的展示和数学直观性的背景关注较少，所以讲解得很吃力，可能部分学生也只是机械地了解了答案而已。

2.2县市决赛——初步引入实验思想解读本例。

由于以第一名的成绩从南片出现，因此还得参加昆山市级决赛，课题还是《等可能性》。

新的课程理念要求教师在概念教学中注重知识的生成，引导学生从已有的知识背景和活动经验出发，提供给学生大量操作、思考与交流的机会，让他们经历观察、实验、猜测、推理、交流与反思等过程，进而在增加感性认识的基础上，帮助学生形成数学概念。基于这一教学理念，本轮在对这道例题的处理上严谨深刻了很多。

笔者设计了如下教学过程：

首先让学生讨论小明和小丽两位同学的看法，并形成了初步的意见：小丽同学说法正确。

然后设计了摸球实验：

实验分成A、B两大组，每个大组分六个小组。A组依据小明同学看法设计，盒中两个红球（没有编号）和一个白球。B组依据小丽同学看法设计，盒中两个红球（编号为红球1、红球2）和一个白球。

组长拿盒子，组织好游戏，书记负责记录（画正字）组员负责轮流摸球，摸球次数20次，要求安静、迅速、守秩序。

各小组完成下列表格数据，最后小组汇总到总表格：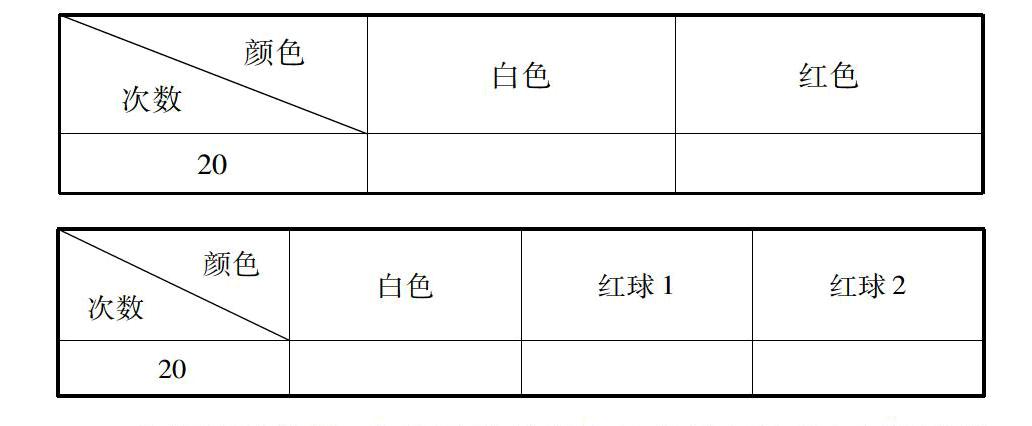

分析所得数据，此处只采用定性分析的方法（因为限于时间和实验次数实际结果同理想结果会出现偏差）。

由A组实验数据可看出红球的次数要远多一些，可见小明同学的说法是不恰当的。由B组数据可得白球，红球1、红球2的次数比较靠近，因此如果把红球编号为红球1、红球2则抽出的结果有三个：白球，红球1、红球2。而且这三个事件是等可能的，从而证实了同学们的猜想。

第二次对例题的解读已经有些接近课标对实验教学的要求，也经历了猜想，实验、验证的过程。但是在教后反思中，发现实验过程的安排缺少条理，为做实验而做实验，实验的目的，实验的步骤及最后对实验数据的分析，实验最后得到了什么结论，都没有完全科学地展示出来。

2.3地市决赛——完成用实验思想解读本例。

比赛结果我以第一名的成绩参加苏州市的决赛，课题还是《等可能》。这次更是不敢掉以轻心，对每个教学程序都做了精心的策划和安排，对本例更是做了精彩的解读和发挥。

第一步：让学生猜想哪位同学的说法正确，并做简单的分析和解释。

第二步：带着上述猜想，进入我设计的实验程序。

实验规则：（1）、（2）与昆山比赛设计相同，增加了以下规则：

（3）A组一次摸球只需要记录是红球还是白球。B组则需要记录白球，红球1、红球2.

（4）每次摸完放回，摇匀再摸。

（5）摸球时不要用眼睛看。

（6）把实验报告单填写完整。

小组实验记录：对应颜色的球下面画正字。

第三步，小组汇总到总表格（表格设计同前）：

实验结果（A）组：我们组共摸球？摇 ？摇次，其中摸到白球？摇 ？摇次，红球？摇 ？摇次，摸到？摇 ？摇球的次数多。实验证明：因为盒中有红球？摇 ？摇个白球？摇 ？摇个，所以摸到？摇 ？摇。

实验结果（B）组：我们组共摸球？摇 ？摇次，其中摸到白球？摇 ？摇次，红球1？摇 ？摇次，红球2？摇 ？摇次。实验证明：由于红球有2个，如果把它们编号为红球1、红球2，那么搅匀后从中任意摸出1个球有？摇 ？摇种可能，而且可能性？摇 ？摇。

第四步，实验结论：

（1）由于这3个球除颜色外都相同，因此搅匀后从中任意摸出1个球，摸到每一个球的可能性是相同的。

（2）由于红球有2个，如果把它们编号为红球1、红球2，那么，搅匀后从中任意摸出1个球有3种可能的结果：

摸出白球，摸出红球1，摸出红球2。并且这3种结果是等可能的，因此摸到红球的可能性大。

（3）由此说明，小明的说法是不正确的，小丽的说法正确。

第五步，结论推广：

像例3这样，由于同色球数量不对称，而导致摸球结果不等可能的例子，通过什么样的方法能使实验的结果具有等可能性？

最后，结论应用：一只不透明的袋子装有2个白球和3个红球，这些球除颜色不同外，其他都相同，搅匀后从中任意摸出1个球，有哪些等可能的结果？

通过本次实验该例题的解读和价值完全被展示出来，而且实验的程序完全合乎科学的规则。

首先，从实验程序来说，从猜想—实验验证—获取原始数据—小组收集数据—全班收集数据—分析数据—得出结论—结论的深化—深化后的挖掘运用，是一套科学的实验程序，组织的有条不紊。

其次：对实验数据的分析，从小组结论——全班结论真正体现了收集到的数据的统计价值，A组的结论证明了（1）：由于这3个球除颜色外都相同，所以搅匀后从中任意摸出1个球，摸到每一个球的可能性是相同的。B组的结论证明了（2）：由于红球有2个，如果把它们编号为红球1、红球2，那么，搅匀后从中任意摸出1个球有3种可能的结果：摸出白球，摸出红球1，摸出红球2.并且这3种结果是等可能的，因此摸到红球的可能性大。这样的分析给学生提展示了一个完整的数据分析的方法，直观明了。

再次，对结论（2）的推广有目的地解决了本节课的一个教学目标和教学难点即会列出一些类型的随机试验的所有可能结果，而这道例题的价值也正是体现在这里。

在教授这节内容的过程中，大多数教师可能只是按照作者最初的想法对这道例题进行了教学，但是现在看来，这样的处理方法是没有准确理解教材提供这道例题的目的，也没有完全认识到这道题所体现的价值。所以在课堂教学中引入数学实验是引导学生发现问题、提出猜想，验证猜想和创造性地解决问题的有效途径，也是完善学生认知结构，提高学生数学素养的重要途径。

3.问题的反思

经过课改的有效宣传，我们基本都已经接受实验必须进入数学课堂的理念，但是很多课堂教学中出现大量为实验而实验的情况。到底如何让数学实验有效地与数学课堂紧密结合是值得广大教师深思的问题，可以从以下方面入手。

3.1认真研读教材，研读教学大纲准确把握教学目标教学难点。

只有在完全解读了教学内容之后才能在适当的地方设计合适的实验，例如对本例题的实验设计是基于会列出一些类型的随机试验的所有可能结果的教学目标，通过设计红球1、红球2，然后进行摸球实验，通过数据的分析学生直观体会到原来对于这样的例题需要用编号的方法把不是等可能性的结果改编成具有等可能性的结果。

3.2选好实验对象后要精心设计实验程序。

老师在设计实验程序时要认真构思实验过程中的每个环节，对实验中可能出现的问题、现象、失败的原因要尽可能考虑得细致，不能单为做实验而做实验，要系统全面地分析实验目的、操作要求、步骤等。

在考虑本例的实验过程中，先让学生提出猜想，然后验证猜想，最后分析实验得到的数据，最后归纳出本例的三点结论，并根据教学目标适时对第二点结论进行拓展，所以实验的安排非常合乎科学研究的程序。

3.3对实验所得到的结果要进行多维度的分析。

上述例题中，对A组的数据进行分析，可以得到如下结论：袋中的三个球被摸到的可能性都是一样的，又因为有两个红球，所以实验得到的数据明显偏向红球。

对B组数据进行分析，可以得到如下结论：如果把红球编号为红球1、红球2，则袋中有三个对象，白球，红球1、红球2，且他们被摸到是等可能的，再由此引申就可以得到用编号的方法可以列举等可能事件。

参考文献：

[1]中国教育部.数学课程标准.北京师范大学出版社，2002.

[2]苏科版实验教科书九年级（上）.江苏科学技术出版社，2012.11.