怀疑逻辑的弗协调方案探赜

周龙生

(北京大学 哲学系，北京　100871)



怀疑逻辑的弗协调方案探赜

周龙生

(北京大学 哲学系，北京100871)

摘要：目的 提供一个建立在弗协调认知逻辑基础上的包含三分认知世界思想的怀疑逻辑构造方案。方法 在系统SPN内定义相关的认知模态算子。结果 怀疑逻辑三分认知世界的设想得以实现，同时由于弗协调认知逻辑的原因，一些怀疑逻辑公式的有效性发生了变化。

关键词：怀疑逻辑；三分认知世界；弗协调认知逻辑

一、怀疑逻辑与三分认知世界

人们在许多领域要运用关于怀疑的推理。怀疑逻辑的提出对于怀疑这一认知模态词作逻辑分析提供了可能。关于怀疑算子的性质是通过一系列怀疑公理[1]的设想来刻画的。如下所示，其中怀疑算子用“D”表示。

D2:Dq→D(p→q) ∨Dp

D4:D(p∨q)→Dp∧Dq

D5:D(p∧q)→Dp∨Dq

其中公理D8被称为“笛卡尔公理”，即如果怀疑p，那么对怀疑p是不可怀疑的。笛卡尔的名言“我思，故我在”在此可理解为：我怀疑，但我当下的怀疑是不可怀疑的。“公理D8为‘我思，故我在’的形式化。”[1]

“人的认知世界可划分为三个部分：信念世界(WB)、怀疑世界(WD)和无知世界(WU)。这三个世界是命题组成的集合，组成它们的元素是认知命题。”[2]

信念世界是指某人所相信的命题所组成的世界，即信念组成的集合。某个命题p属于信念世界，记作Bp。怀疑世界是由认知主体怀疑的那些命题组成的。某个命题p是怀疑世界的一个元素记为Dp。无知世界“是由那些主体没有‘考虑’的命题所构成。对于这些命题(以及它们的否定)，认知主体从没有‘接触’到它们，主体对它们一无所知，或者主体虽然‘接触’过它们，但不清楚它们的意义，因而主体既不相信它们，也不怀疑它们”[2]。主体对p无知，记为Up。3个认知世界之间的关系是：信念世界(WB)、怀疑世界(WD)和无知世界(WU)共同组成整个认知世界，并且这3个世界不会相互重叠。三者的关系如图1所示。

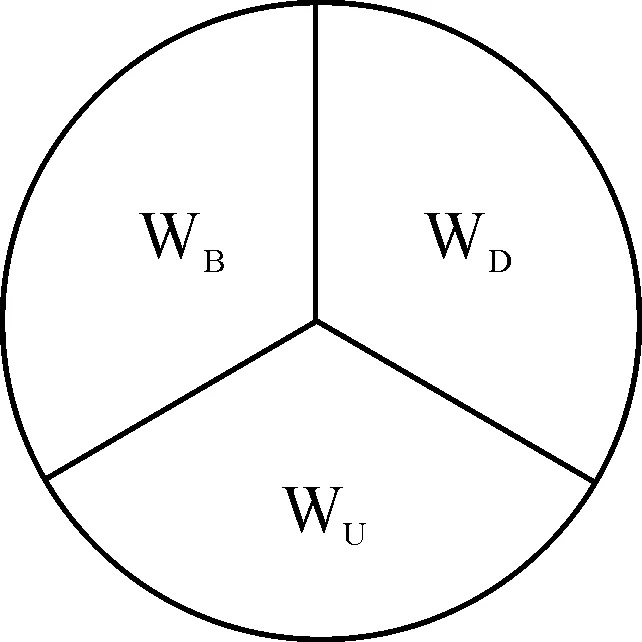
图1　设想中的认知世界关系

二、弗协调认知逻辑SPN

定义(LPN)弗协调认知逻辑SPN使用的形式语言LPN,是由弗协调命题逻辑的语言加认知算子※得到的。LPN包括4类初始符号：

[1] 命题符：p1，p2，p3，…，pk，…；k为自然数；

[3] 认知联结符：※；

[4] 标点符：(，)。

定义(Expr(LPN))一个由形式语言LPN中符号构成的任意有穷序列称为一个表达式，全体表达式组成的集合记为Expr(LPN)。

定义(Atom(LPN))A∈Atom(LPN)，即LPN中的一个表达式A是原子公式，当且仅当A是一个单独的命题符。

定义(Form(LPN))A∈Form(LPN)，即LPN中的一个表达式A是公式，当且仅当它能由(有穷次使用)下列规则得到：

[1] Atom(LPN) ⊆Form (LPN)，即原子公式是公式；

[3] 如果A，B∈Form(LPN)，则(A∧B)，(A∨B)，(A→B)∈Form(LPN)。

为叙述方便，引进以下缩写符号：

(A↔B)是指(A→B)∧(B→A)；

Ak指A00…0，这里一共有k个0，其中k为自然数；

A(n)指(…(A1∧ A2) ∧ A3∧…∧An)；

弗协调认知逻辑的公理系统是在科斯塔的弗协调命题逻辑系统Cn(1≤n<ω)上增加含认知算子※的若干公理以及新的推理规则构成。公理模式如下：

(Ax1)至(Ax12)所有Cn(1≤n<ω)的公理模式[3]

(Ax13) A(n)→(※A)(n)

(Ax14) ※(A→B) →(※A→※B)

(Ax15) ※A→A

分离规则(MP)：如果├A，├A→B，那么├B；

认知规则(N)：如果├A，那么├※A。

定义(框架、SPN框架)设〈W，R〉是任一二元组，〈W，R〉是一个正规框架(简称框架)，当且仅当，W是任一非空集，R是W上的任一二元关系，即R⊆W×W。

一个SPN框架，表示为FSPN，是同时满足下述条件的一个框架〈W，R〉，对于所有的w∈W，

[1] ∀w(Rww)；

[2] ∀w∀w′∀w′′ (Rww′∧ Rw′w″→Rww″)。

定义(赋值)设〈W，R〉是任一框架，V是〈W，R〉上对LPN公式的一个赋值，当且仅当，V是LPN公式集Form(LPN)与W的笛卡尔积Form(LPN) ×W到集合{1，0}上的映射，即

V： Form(LPN)×W → {1，0}

通过分析及居民生态城市和城市林业的内涵和特点，宣传在构建生态城市建设中发展城市林业的作用，提出推进城市林业和生态城市可持续发展的建议，充分发挥城市林业在构建生态城市中的作用。让每一位公民参与到建设生态城市的工程中，全力打造一个生态良好的发展中城市，为我国生态环境的改善及生态经济的发展贡献力量。

并满足以下条件：对任意的LPN公式A、B，任意的w∈W，

[4] V(A→B，w)=1 ⟺ V(A，w)=0或者V(B，w)=1；

[5] V(A∧B，w)=1 ⟺ V(A，w)=V(B，w)=1；

[6] V(A∨B，w)=1 ⟺ V(A，w)=1或者V(B，w)=1；

[8] V(※A，w)=1 ⟺ 对于任一w′ ∈W，若Rww′，则V(A，w′)=1。

定理如果V是框架F上的一个赋值，那么对任意的A∈Form(LPN)，w∈W：

[3] V(A，w)=0 ⟺ V(～A，w)=1；

[6] V(※※A，w)=1 ⟺ 对于任意的w，w′，w″∈W，如果Rww′并且Rw′w″，则V(A，w″)=1。

弗协调认知逻辑系统SPN具有可靠性和完备性。相关证明参见张清宇的《弗协调逻辑》[4]。

三、SPN与三分认知世界

表1　真值组合1

表2　真值组合2

由表1可知，我们定义“相信”和“怀疑”这两个算子时，如果采取如下方法：

则公式Bp∧Dp是可满足的，即存在某个认知状态w∈W，使得V(Bp∧Dp，w)=1，也就是说在某个认知状态w中有命题p既属于信念世界WB，又属于怀疑世界WD。并且可以看出，对于任何w∈W，都有V(Bp∨Dp，w)=1成立，即在状态w中不存在既不属于信念世界WB又不属于怀疑世界WD的认知命题。这样构成的认知状态中，无知世界WU变为空集了。如图2所示。

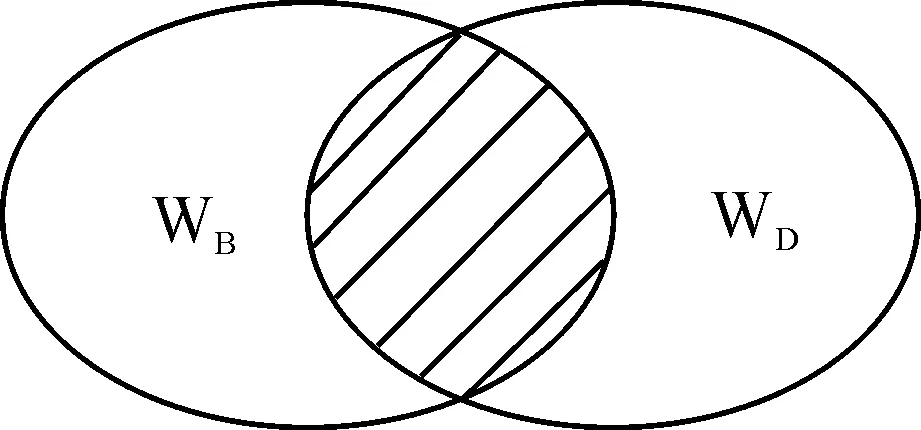
图2　SPN中的一种认知世界关系

其中W=WB∪WD，阴影部分显示的是满足Bp∧Dp的认知命题集合。这样的定义与怀疑逻辑的本意和三分认知世界的思想相去甚远。

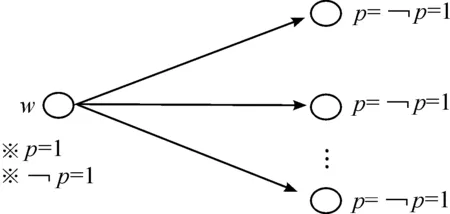
表3　真值组合3

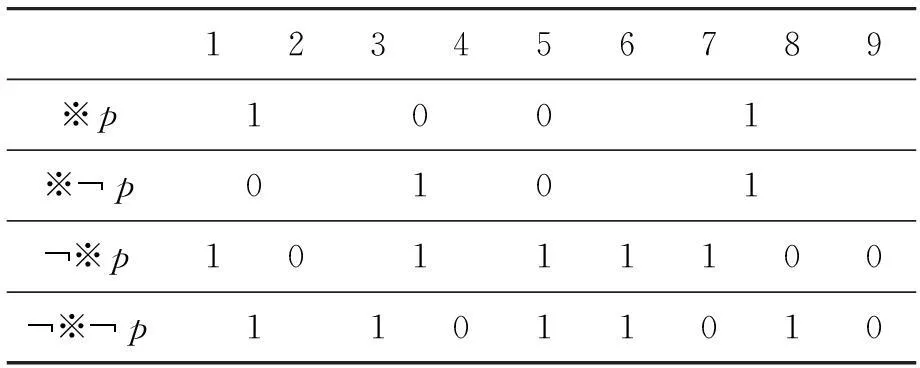
表4　真值组合4

于是，我们得到如下定义：

从得出定义的过程来看，满足Up的认知命题集，不会和满足Bp或者满足Dp的命题集相交，即不存在既属于信念世界又属于无知世界，或者既属于怀疑世界又属于无知世界的认知命题。

以上3组定义的生成和语义证明的过程可以用下面关系图表示：

表4列出了各认知命题间所有可能的真值关系。因此，对于所有的认知命题而言，要么满足公式Bp，要么满足公式Dp，要么满足公式Up；由这些认知命题构成的与之相应的信念世界、怀疑世界以及无知世界构成了全部的认知世界。

至此，我们在弗协调认知逻辑系统SPN内对于相关认知算子的定义，以及随之确定的3组命题集合，体现了三分认知世界的思想，保证了3个世界的性质与关系得到实现。

即两个互相矛盾的命题可以同时成为我们的信念。这样的结果在三分认知世界理论的最初设想中是不存在的，之所以得到这样的结果，是因为弗协调方案所致。

四、SPN与怀疑逻辑

以下是一些怀疑逻辑的SPN系统内定理：

SPND1: Dq→D(p→q)∨Dp

SPND3: D(p∨q)→Dp∧Dq

SPND4: D(p∧q)→Dp∨Dq

SPND6: D(p∧～p)

SPND7: ～Dp→～D～Dp

SPND9: Dq∧～Dp→D(p→q)

例1：D(p∧～p)是系统内定理

证明：

1. ※p→p

2.～p→～※p

3. ～～p→～※～p

4.p→～※～p

5.※p→～※～p

6.※～p→～※p

7.※～(p∧～p)→～※(p∧～p)

8. ～(p∧～p)

9. ※～(p∧～p)

10. ～※(p∧～p)

11.D(p∧～p)

例3：Dp→～DDp(笛卡尔公理)不是SPN系统内定理。

Dp→～DDp存在SPN框架上的反模型，如下所示。

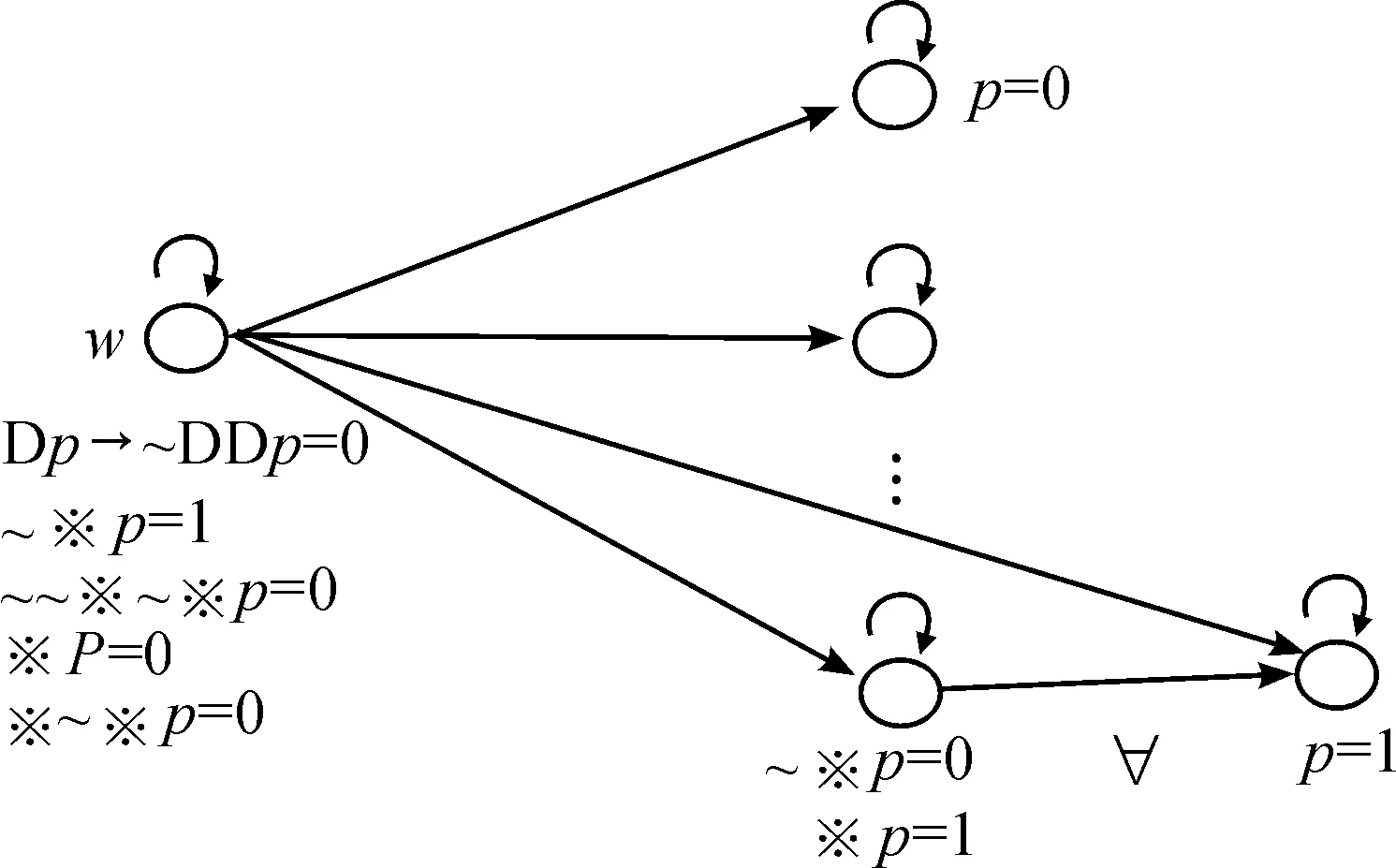
笛卡尔公理Dp→～DDp在SPN系统内的失效，说明了笛卡尔公理对于SPN系统的独立性，也说明了笛卡尔公理和其他的怀疑逻辑公理在刻画关于“怀疑”认知模态词的性质上的层次差异。然而，我们可以在SPN的基础上，将笛卡尔公理Dp→～DDp作为新的系统公理引入，构建新的形式系统。或者增加一条可以推演出笛卡尔公理的系统公理，例如：

(Ax17) ～※～A→※～※～A，

得到新系统SPN*，则笛卡尔公理Dp→～DDp在SPN*内是可证的。

证明：

1. ～※～～p→※～※～～p

2.※～※～～p→ ～～※～※～～p

3. ～※～～p→ ～～※～※～～p

4. ～※p→ ～～※～※p

5.Dp→～DDp

参考文献：

[1]潘天群.建立在“笛卡尔公理”上的一个怀疑逻辑系统[J].湖南科技大学学报(社会科学版),2004(9):33-36.

[2]潘天群.三分的认知世界与怀疑逻辑的独立性[J].湖南科技大学学报(社会科学版),2005(9):39-41.

[3]杜国平.经典逻辑与非经典逻辑基础[M].北京：高等教育出版社,2006.

[4]张清宇.弗协调逻辑[M].北京：中国社会出版社,2003.

[5]周北海.模态逻辑导论[M].北京：北京大学出版社,1997.

(责任编辑张佑法)

Preliminary Analysis of Paraconsistent Doubting Logic

ZHOU Long-sheng

(Department of Philosophy, Peking University, Beijing 100871, China)

Abstract:Objective This paper aimed to provide a formalization of doubting logic with tri-partitioning of epistemic worlds based on paraconsistent epistemic logic. Method We defined the related epistemic modal operator in SPN. Result The idea of tri-partitioning of epistemic worlds was achieved. Meanwhile, the validity of some formulas about doubting logic was changed for the paraconsistent epistemic logic reasons.

Key words:doubting logic; tri-partitioning of epistemic world; paraconsistent epistemic logic

中图分类号：B81

文献标识码：A

文章编号：1674-8425(2016)03-0025-06

作者简介：周龙生(1981—)，男，山东枣庄人，博士研究生，研究方向：符号逻辑。

基金项目：国家社会科学基金重大项目“应用逻辑与逻辑应用研究”(14ZDB014)

收稿日期：2015-08-09

doi:10.3969/j.issn.1674-8425(s).2016.03.005

引用格式：周龙生.怀疑逻辑的弗协调方案探赜[J].重庆理工大学学报(社会科学)，2016(3):25-30.

Citation format：ZHOU Long-sheng.Preliminary Analysis of Paraconsistent Doubting Logic[J].Journal of Chongqing University of Technology(Social Science)，2016(3):25-30.