一种新型混合并行粒子滤波频率估计方法

王　伟,余玉揆,郝燕玲

(哈尔滨工程大学自动化学院,哈尔滨,150001)



一种新型混合并行粒子滤波频率估计方法

王伟,余玉揆,郝燕玲

(哈尔滨工程大学自动化学院,哈尔滨,150001)

摘要：针对高动态、低信噪比环境下的载波频率信号跟踪问题,提出一种新的混合并行粒子滤波算法(Multiple Extend Kalman Filter Independent Metropolis Hastings,M-E-IMH).该算法具有并行运算结构,实时性较基本粒子滤波有较大的提高.该算法直接利用同相支路(In-phase,I)和正交支路(Quadrature,Q)作为观测量,避免了传统方法中的鉴别器引入而引起的信噪比损耗.在高斯和非高斯环境下,与现有的载波跟踪方法如扩展卡尔曼滤波器(EKF),粒子滤波器(PF),卡尔曼滤波器(KF)等仿真对比表明,该方法在低信噪比下具有更高的跟踪精度.

关键词:多普勒频率估计;并行粒子滤波;高动态;非高斯噪声;实时性

1引言

多普勒频率信号跟踪可见于各种数字通信系统,尤其是对GPS接收机,雷达而言,精确的频率估计和跟踪是能否正常工作的基础.当GPS接收机或者雷达探测的目标处于高动态环境时,即载体运动具有较高的速度、加速度、加加速度,会使得载波跟踪环路输入的载波频率信号产生较大的多普勒频移、多普勒频移变化率、多普勒二次变化率.此时对于普通的载波跟踪环路而言,必须增大载波跟踪环路的带宽,但这样会导致宽带噪声的增加,使得载波跟踪精度降低,特别在低信噪比下,噪声电平超过环路工作门限时将导致载波跟踪环路失锁[1].在低信噪比,高动态环境下,载波频率信号跟踪环路是频率估计中的难点和重点.

针对上述问题,国内外学者提出了许多解决方法,文献[1]中的最大似然估计(Maximum Likelihood Estimation,MLE)、文献[2]中扩展卡尔曼滤波(Extended Kalman Filter,EKF)、文献[3]中无迹卡尔曼滤波(Unscented Kalman Filtering,UKF)等,但它们属于开环控制,无法实时跟踪与解调.而文献[4]中的EKF为闭环跟踪,但只适用于单载波的无积分-清除环路.文献[5]中提出了有鉴别器辅助的线性Kalman Filter (KF)跟踪算法,但鉴别器需要占用一定的系统带宽,这将降低环路的信噪比,且高动态属于非线性模型,非线性模型的线性化造成的损失将使得KF环路的滤波精度降低.文献[6]提出无鉴相器辅助的EKF载波跟踪环,其模型基于线性高斯噪声假设,实际的高动态应用环境中,如战斗机、导弹等,系统受到的干扰将不可避免的存在非高斯噪声.文献[7]中将基本粒子滤波Particle Filter (PF)应用到多普勒频率估计中,但PF实时性较差[8],无法进行实时解调.

鉴于上述考虑,本文提出一种由两个EKF模块和一个Independent Metropolis Hastings (IMH)模块组成的新的载波频率信号跟踪滤波方法，称为M-E-IMH.其利用In-phase and Quadrature (IQ)支路输出作为观测量,以EKF所得量作为其重要性密度函数,使得重要性密度函数向后验概率密度函数移动,同时IMH重采样实现并行运算,避免了粒子滤波中权重归一化引起的并行运算瓶颈问题,提高了实时性,最后再次利用EKF使得粒子更接近真实值,进而降低了滤波所需的粒子数目.通过两种不同观测噪声(高斯、非高斯)环境下的仿真,验证了算法优越性.

2基于并行粒子滤波的载波跟踪环路

2.1粒子滤波跟踪环路结构

基于PF的载波跟踪环的原理框如图1所示,其中SIF(n)为中频信号,可以表示为:

SIF(tk)=A(tk)cos(ωIFtk+θk+φ0)+nk

(1)

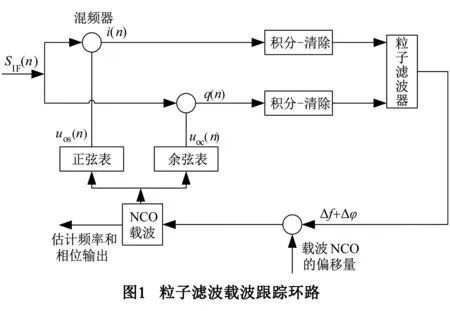
其中tk=iT,T为环路更新时间,即相干积分时间,设为1ms,采样频率为10MHz,A(tk)为载波振幅,载波振幅A(tk)设为1,ωIF为中频,θk为由多普勒频移而产生的载波相位变化量,φ0为初相位.

假设收到的信号受到零均值,平稳、窄带高斯白噪声nk的干扰,方差为σ2.信噪比SNR=A2/(2σ2).两路正交的本地载波信号由NCO产生:

(2)

其中ω0为本地复现的角频率.

环路输入信号和本地信号经过混频器后:

(3)

其中ωek表示k时刻载波频率跟NCO本地复现频率之差,θek表示相位差,此时噪声仍为高斯白噪声[6],均值为0,方差变为δ2/2.经积分-清除后,滤除高频信号成分和噪声[9]:

(4)

传统载波跟踪算法利用鉴相或鉴频器得到残留相位或残留频率,作为KF,EKF,MLE等滤波方法的量测值,但鉴别器需要足够高的信噪比,且需占用一定的带宽.为了在低信噪比的环境下能良好的工作,本文直接利用IQ支路作为量测值[6].

粒子滤波器具有简单、易于实现等特点,为非线性非高斯动态系统提供了一种有效的解决方法.根据以上分析,建立载波跟踪的非线性动态模型如下:

Xk+1=φXk+BUk+Q

(5)

Zk+1=h(Xk+1)+R

(6)

式(5)和式(6)分别为量测方程和观测方程,式中Xk和Zk分别表示第k时刻的状态向量和观测向量;h(·)为状态向量和观测向量之间的非线性函数;φ为状态转移矩阵;Uk和B分别为输入信号及输入所对应的矩阵;Q为状态转移噪声向量;R为观测噪声向量.

2.2量测方程

在k-1时刻,载波的初始相位,多普勒角频移和一阶变化率分别设为φ0(k-1),ωd(k-1),ωa(k-1),则第k时刻载波的各参数为:

(7)

其中q(k-1)=[q1(k-1)q2(k-1)q3(k-1)]T为零均值正态不相关的状态噪声,有如下形式:

(8)

其中Y(t)表示二阶变化率的抖动情况.设k时刻本地NCO初始相位为θnco(k),角频移为ωnco(k),则:

θnco(k)=θnco(k-1)+ωnco(k-1)T

(9)

设k时刻NCO和载波的相位误差为θe(k-1)=φ0(k-1)-θnco(k-1),则:

θe(k)=φ0(k)-θnco(k)

-ωnco(k-1)T+q1(k-1)

设Xk=[θeωdωa]k,则状态转移方程表示为:

(10)

其中Q为零均值的协方差矩阵.

(11)

其中Y(k)代表频率的二阶变化率的抖动情况.

本文采用的多普勒频率变化模型为JPL定义的高动态模型[9],针对不同的SNR,同样的模型中频率的二阶变化率的抖动情况Y(k)值应保持相同,可以算出Y=1E6,加上噪声,本文取Y=1E7.量测方程中φ,Uk和B的定义如下:

(12)

(13)

Uk=ωnco(k)

(14)

2.3观测方程

鉴于粒子滤波器对非线性非高斯模型的有效性,本文采用IQ支路的输出作为观测值:

(15)

(16)

(17)

观测方程可表示为:

(18)

(19)

将Xk=[θeωdωa]k中的θe反馈回NCO,进行本地载波的调整,反馈量为wnco=θe/dt+ωd.

3新型并行粒子滤波算法M-E-IMH

粒子滤波通过非参数化的蒙特卡洛(Monte Carlo)模拟方法来实现递推贝叶斯滤波,适用于任何能用状态空间模型描述的非线性系统,精度可以逼近最优估计,为分析非线性动态系统提供了一种有效的解决方法.

基本粒子滤波算法存在精度不高、实时性差等缺陷.针对其精度不高缺陷,许多改进型的粒子滤波如EPF[10]、UPF[11]等被提出,但这些方法主要在重要性密度函数环节进行改进,并未解决粒子滤波的实时性差的问题.本文提出一种新的并行混合粒子滤波算法,对重要性密度函数选择和重采样部分进行优化改进,使得其重要性密度函数更加接近后验概率密度函数,算法为并行结构,实时性得到提高,过程如下:

(1)基本粒子滤波PF采用先验概率密度函数作为重要性密度函数,并未考虑观测值,使得xk依赖模型,如果模型不准确,或者量测噪声突然加大,先验概率密度函数将不能有效地描述概率密度函数的真实分布.本文采用EPF思想,利用EKF结合最新的观测值得到xk后验概率密度作为粒子滤波的重要性密度函数.

(2)基本粒子滤波PF在重采样之前需进行权值归一化[8],即只有在所有的粒子全部产生,计算权值并归一化后才能进行重采样,这也是粒子滤波并行实现的瓶颈所在,同时基本重采样算法还会造成粒子样本枯竭.本文在粒子滤波重采样部分引入IMH算法,用于解决了粒子滤波并行运行瓶颈问题,增强了粒子的多样性.

IMH算法是一种特殊的Metropolis-Hastings算法,其建议转移函数T(x,y)为独立实验密度g(y),经过IMH算法产生的建议移动点独立于前一个状态xk-1.在信号处理中的IMH算法为主要为如下两步:

步骤1从g(·)中独立地产生一潜在的转移点y并计算其权值

(20)

其中p(·)为先验概率密度函数.可以看出IMH算法在粒子的权值计算完后即可进行粒子的取舍,避免了传统的粒子滤波算法并行瓶颈问题[8].

(3) 以EKF作为粒子滤波的重要性密度函数的EPF,在量测噪声较高时,得到的滤波精度较低.本文提出在EPF后再加入一步EKF,即以前一步的EPF得到的方差和状态量再进行一次EKF.EPF算法可最大限度地消除系统的非线性效应,即非线性系统经过EPF后可看成一弱非线性系统,此时再进行EKF滤波将达到最佳滤波效果.

整个算法结构为一个汉堡结构,由两个EKF夹着一个粒子滤波算法,相当于Iterated Extended Kalman Filter (IEKF)算法[12]中插入了一个粒子滤波算法,增强了IEKF的非线性处理能力,提高了粒子滤波算法精度.

M-E-IMH算法步骤如下:

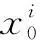
步骤2对于k=1,2…,将有如下5个步骤.

step1:重要性采样.

①从{1,2,…,N}中产生N+Nb个标志量J(i),i=1,2,…,N-Nb,其中Nb为burn-in阶段所需的粒子数(Markov链从初始状态转移到收敛稳态的过程称为burn-in阶段,Nb的大小跟初始值的选取有关,一般按经验选取),N为所需的粒子数目.

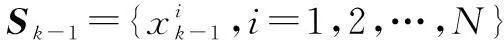
(21)

(22)

(23)

(24)

(25)

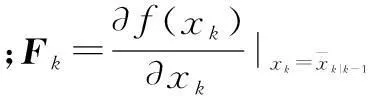
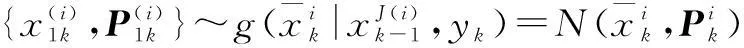
step2:权值计算.

利用权值计算公式:

(26)

step3:IMH采样.

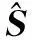
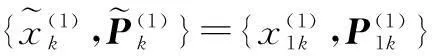
②对于i=2,3,….,N+Nb有:

(27)

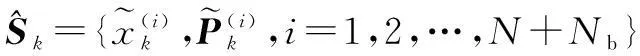
step4:第二阶段EKF更新.

(28)

(29)

(30)

Step5:计算输出.

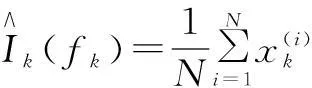
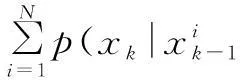
辅助粒子滤波的基本思想是引入一个粒子辅助量用以逼近后验概率密度,构造一个新的状态空间{xk,ζ},其中ζ∈[1,2,…N]代表了粒子索引量i,后验概率密度函数可以表示为:

(31)

选取重要性密度函数使其满足:

(32)

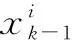
(33)

式(33)避免加和运算,减少了计算量.

在本文中,由于在进行IMH重采样前,已经利用EKF使得每个粒子都结合了最新量测值,定义:

(34)

g(ζ(i))=c

(35)

其中c为常值,此时能在不增加计算量情况下将权值计算由式(26)变为式(33).

基本粒子滤波需等所有的粒子的权值计算完毕后才能进行重采样,重采样成为了其并行运算的瓶颈所在,而M-E-IMH利用IMH采样,使得其具备了并行运算的能力,提高了算法的实时性.

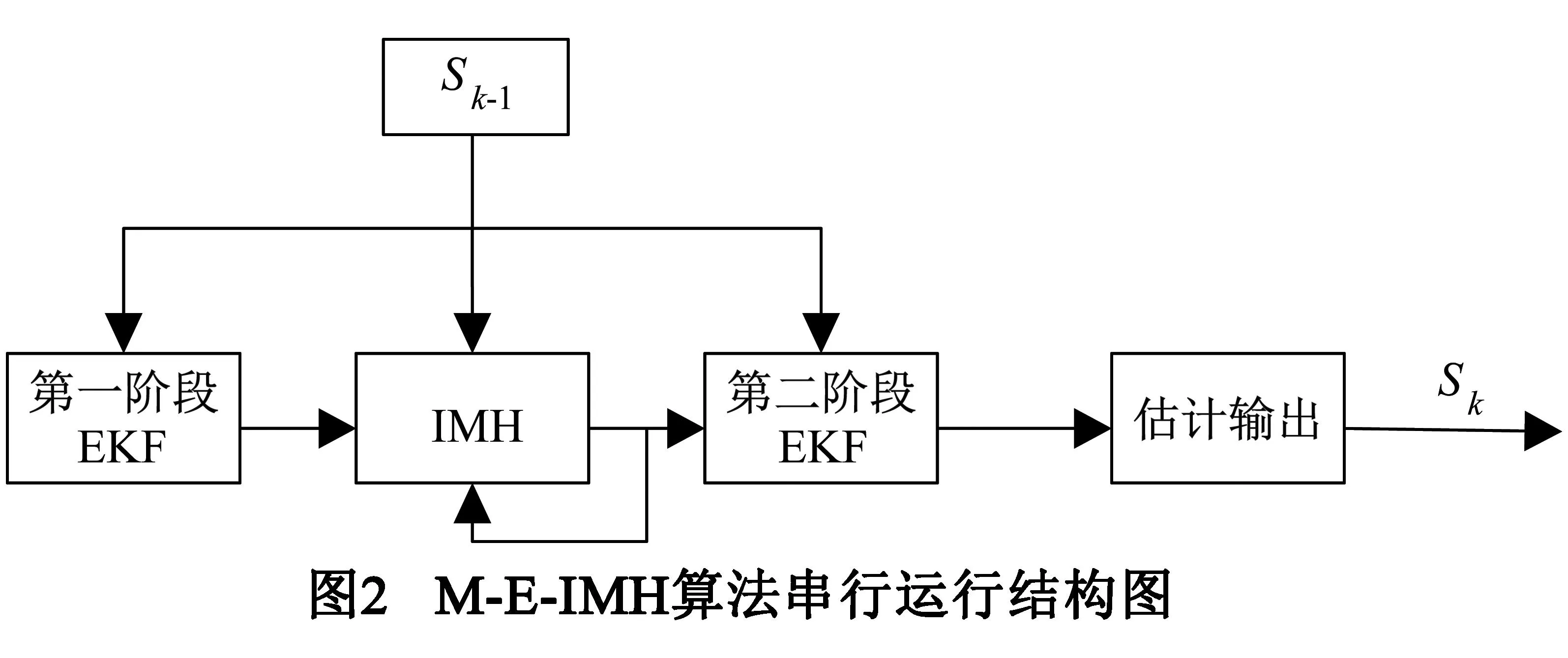
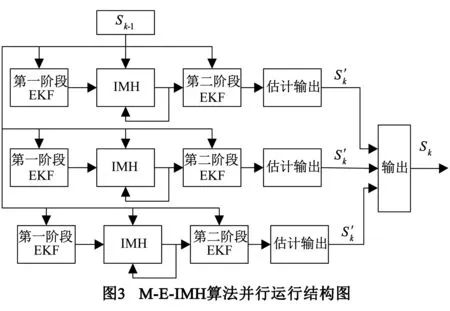
图2为M-E-IMH算法的串行运行结构,其中第一阶段的EKF用于产生IMH的建议分布,其中“第一阶段EKF”、“IMH”、“第二阶段EKF”三个模块的计算可采用流水线式操作.假设“第一阶段EKF”计算一个粒子所需的时间为T1,“IMH”环节所需的时间为T2,“第二阶段EKF”为T3,则产生第一个粒子所需的时间为T1+T2+T3,后续的每个粒子仅需要max(T1,T2,T3).如果估计一个状态需要N+Nb个粒子,则共需要的时间为(N+Nb-1)*max(T1,T2,T3)+T1+T2+T3,较基本粒子滤波算法运算速率得到较大的提高.由于重采样时无需所有的粒子交换信息,可以把重采样分为M个小块,每一个分别各自进行滤波处理,最后汇总输出,形成并行结构,其框图如图3所示.将N+Nb个粒子分为M块,这每一小块需处理N/M+Nb个粒子,如果认为一个粒子在每一小块中所需时间相同的话,则总共需时间为(N/M+Nb-1)*max(T1,T2,T3)+T1+T2+T3,算法实时性得到更大的提高.

4仿真分析

在M-E-IMH估计频率技术仿真模拟中,采用JPL实验室定义的具有典型意义的高动态模拟环境[9],用以模拟频率的快速变化,其参数描述如下:

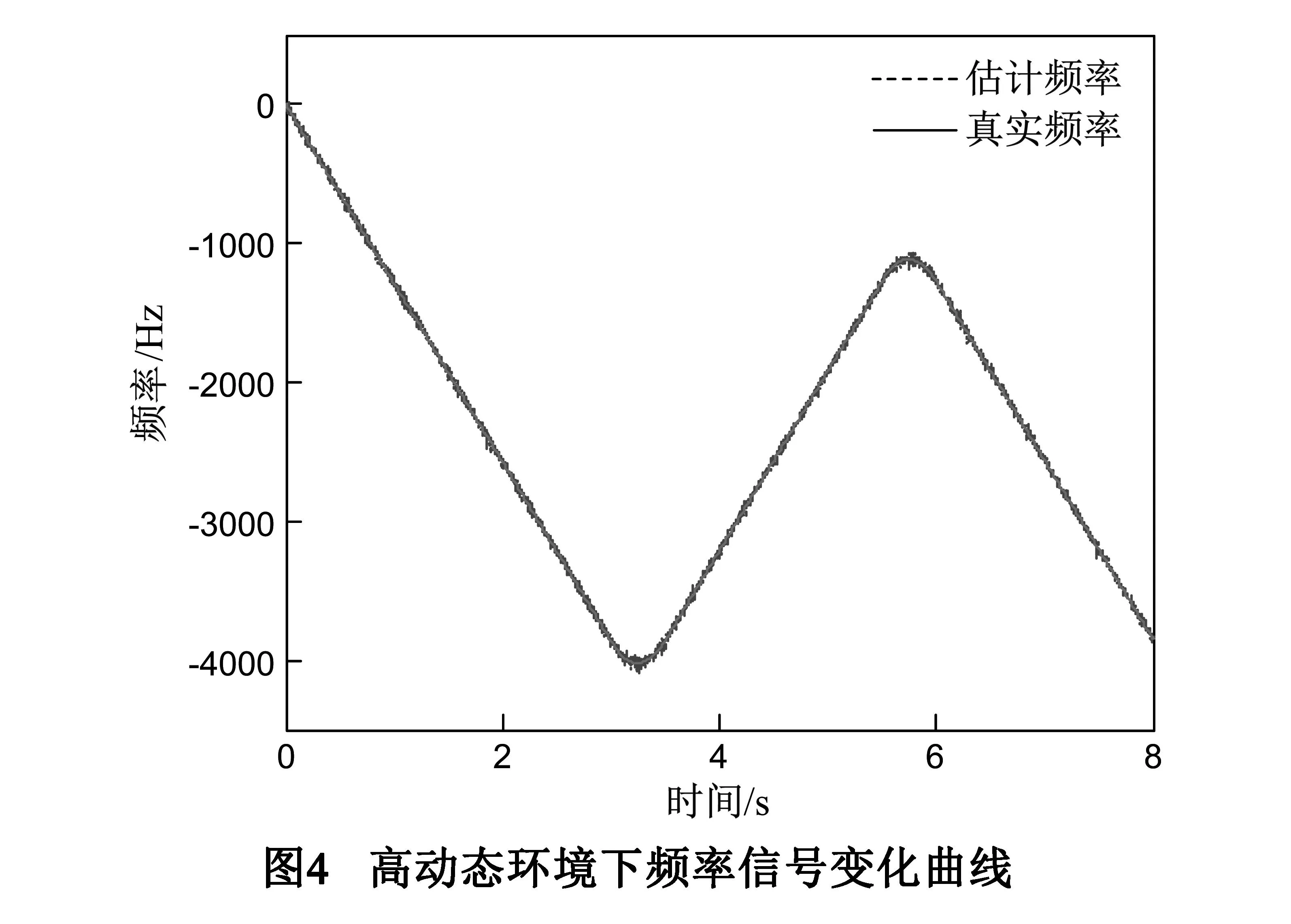
设载体的高动态含有正、负两种加速度变化率脉冲,脉冲持续时间为0.5s,幅度为100g/s,被持续2s的横加速度所分割,加速度的初始值设定为-25g,速度的初始值设定为0m/s.高动态环境下频率信号仿真波形及跟踪曲线如图4所示.

本文将针对高斯白噪声和非高斯噪声两种不同的观测噪声环境下对M-E-IMH算法的性能进行仿真,与其进行对比的环路滤波有:IQ支路的输出直接作为观测量的EKF、粒子数为1000的PF、EPF、M-E-IMH,鉴别器辅助的线性KF.

4.1观测噪声为高斯白噪声

观测噪声为高斯白噪声的仿真环境下,图5给出了基于EKF、PF、KF、EPF和M-E-IMH五种算法在SNR=-25dB时的高动态多普勒频率估计结果.从跟踪结果上看,各算法均能地锁定多普勒频移,其中M-E-IMH算法估计精度最高,可较好地适应高动态环境.

图6为各跟踪环路滤波器在不同的SNR时对测试信号的均方根(Root Mean Square,RMS)频率估计误差.可以看出,在SNR<-20dB低信噪比下,M-E-IMH频率估计效果明显优于其它方法.由于数学模型具有一定的非线性,KF的滤波估计精度较差,EKF次之.EPF估计精度较粒子滤波PF有少量提升,这是由于EPF利用EKF结合观测量更新了先验概率密度函数,使得其更接近实际值,但由于非线性的影响,精度提高有限.但粒子数目相同的情况下EPF、PF并未达到M-E-IMH精度,说明M-E-IMH只需要较少的粒子即能达到基本粒子滤波的估计精度.

总体而言,M-E-IMH在低信噪比下估计精度明显优于其它方法.表1为各算法的每个循环所用的平均时间,数据由MATLAB软件统计所得.

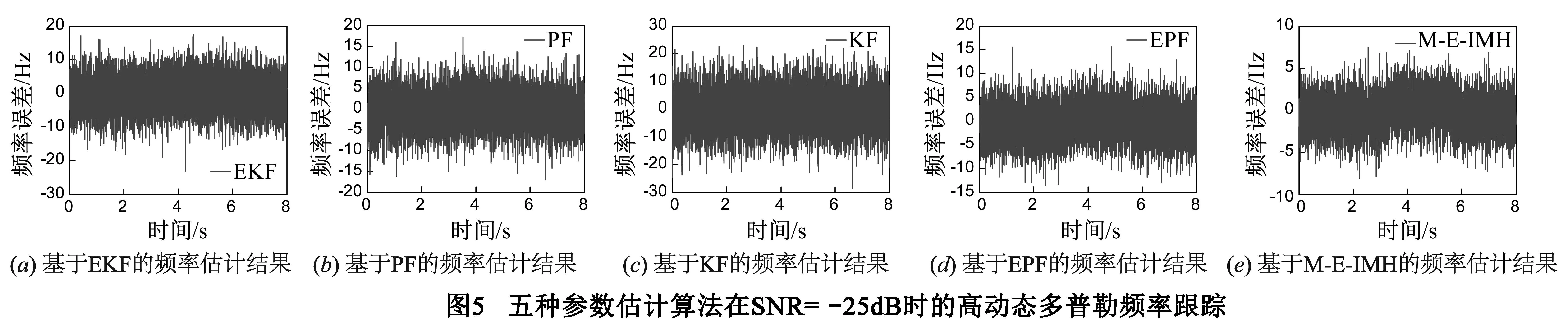
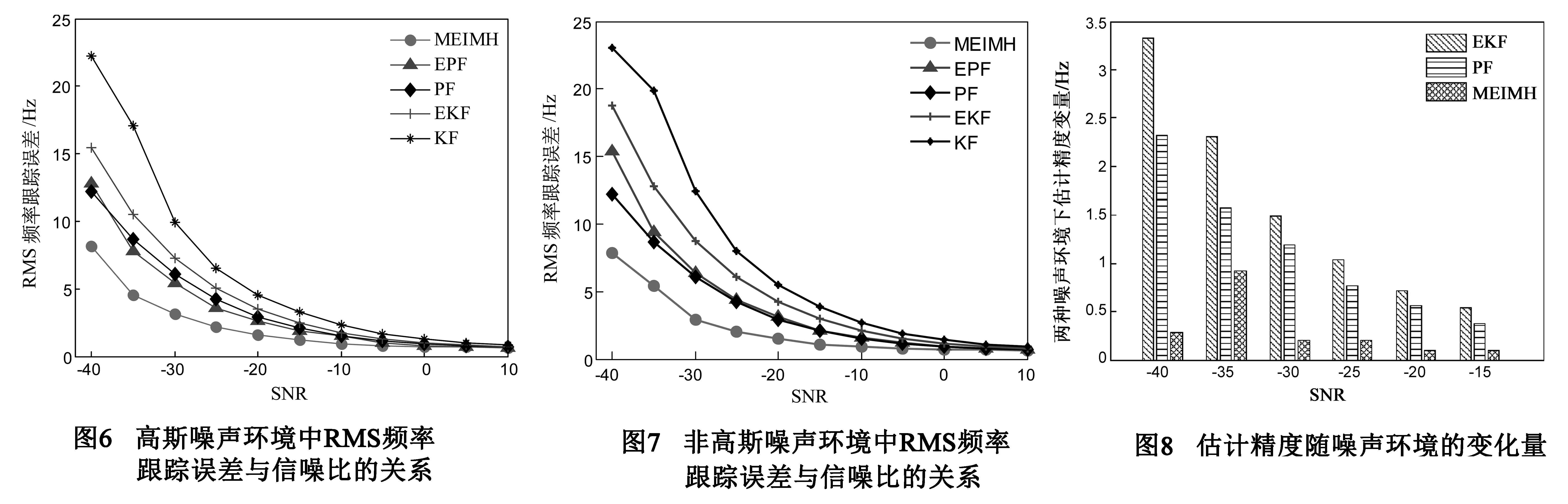
表1　算法所需的平均时间(s)

NEPFPFMEIME10000.550.200.46

从表1可以看出,算法M-E-IMH运算时间上优于EPF算法,而PF算法所需的运算时间最少.由于在MATLAB无法进行并行运算,表1中的M-E-IMH运算时间是基于图2流水线结构而得出的,从算法的流程可知,M-E-IMH较EPF多一个EKF处理模块,但M-E-IMH算法的运算时间乃低于EPF,这说明了M-E-IMH算法流水线结构的优越性.在FPGA(Field Programmable Gate Array)平台中M-E-IMH算法可采用图3的并行结构,由IMH算法的性质可知,只要在每个并行模块中的粒子数使得马尔科夫链能够达到平衡稳态,则并行结构只提高运算效率并不影响算法性能,采用M个并行模块,则并行结构的M-E-IMH所需的运算时间变为串行结构的1/M.M-E-IMH算法若采用4个并行模块,则运算时间变为0.15 s,可以看出采用并行结构的M-E-IMH算法的实时性较PF算法强.

4.2观测噪声为非高斯噪声

本文选取具有普遍意义的闪烁噪声模拟非高斯噪声.闪烁噪声与高斯噪声的主要差别在于尾部较长,而中心区域则类似高斯形状,可以认为闪烁噪声可以分解为高斯噪声和具有“厚尾”特性的噪声之加权和,这里取的“厚尾”分布为大方差的高斯分布.其模型为:

pt(x)=(1-ε)pg(x)+εpl(x)

(36)

其中,pt(·),pg(·),pl(·)分别代表闪烁噪声,高斯,大方差高斯分布.ε表示一个小于1的正数,pg(·)的方差小于pl(·)的方差.本文中,pl(·)的方差为pg(·)方差的10倍,ε=0.05.EKF,KF算法对闪烁噪声采用矩匹配的方法,闪烁噪声的1、2阶矩为:

u=(1-ε)u1+εu2=0

(37)

P=(1-ε)Pg+εPl

(38)

观测噪声为闪烁噪声情况下,载波跟踪环路的仿真结果如图7所示.可知,在非高斯环境下,M-E-IMH较其它方法具有更高精度,说明了M-E-IMH在非高斯噪声环境下的有效性.而EPF此时的估计精度较PF有所降低,其原因在于EKF对非高斯非线性环境的不适应性,使得EKF对先验概率密度函数的估计能力下降,算法精度下降.

图8为各算法在高斯噪声和非高斯噪声环境下的估计精度变化图,可以看出,本文算法M-E-IMH滤波精度变化最小,EKF变化量最大,PF变化居中.进一步说明了M-E-IMH算法对非线性非高斯环境的适应性.

5结论

针对高动态、低信噪比环境下的频率跟踪,本文提出了一种新的混合并行粒子滤波算法M-E-IMH,该算法直接利用积分-清除量作为观测量,避免了鉴相器带来的信噪比损耗及PLL/FLL中的判别门限的设置.算法具有并行结构,分析其运算时间,结果表明较基本PF,实时性得到较大的提高.在高斯和非高斯观测噪声环境下的仿真表明,该方法相对于现有的频率估计方法,如EKF、PF、EPF、KF等,具有更高的频率跟踪精度.

参考文献

[1]向洋,胡修林.基于最大似然函数估计的高动态GPS载波跟踪环[J].电子学报,2010,38(7):1563-1567.

Xiang Yang,Hu Xiu-lin.Maximum likelihood estimation based high dynamic GPS carrier tracking loop[J].Acta Electronica Sinica,2010,38(7):1563-1567.(in Chinese)

[2]Jung H,Psiaki M L.Extended Kalman filter methods for tracking weak GPS signals[A].Proceedings of the ION GPS 2002[C].Portland,OR:ION,2002.2539-2553.

[3]Xi Chen,et al.High dynamic GPS signal tracking based on UKF and carrier aiding technology[A].2010 International Conference on Communications and Mobile Computing (CMC)[C].Shenzhen,China:IEEE,2010.476-478.

[4]Vilnrotter V A,Hinedi S,Kumar R.Frequency estimation techniques for high dynamic trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1989,25(4):559-577.

[5]Miao Jian-feng,Chen Wu,et al.Adaptively robust phase lock loop for low C/N carrier tracking in a GPS software receiver[J].Acta Automatica Sinica,2011,37(1):52-60.

[6]田甜,安建平,王爱华.高动态环境下无数据辅助的扩展Kalman滤波载波跟踪环[J].电子与信息学报,2013,35(1):63-67.

Tian Tian,An Jian-ping,Wang Ai-hua.Non-data-aided extended Kalman filter based carrier tracking loop in high dynamic environment[J].Journal of Electronics & Information Technology,2013,35(1):63-67.(in Chinese)

[7]Sidi A Y,Weiss A J.Delay and Doppler induced direct tracking by particle filter.[J].IEEE Transactions on Aerospace and Electronic Systems,2014,50(1):559-572.

[8]A C Sankaranarayanan,A Srivastava,R Chellappa.Algorithmic and architectural optimizations for computationally efficient particle filtering[J].IEEE Transactions on Image Processing,2008,17(5):737-748.

[9]Vilnrotter V A,Hinedi S,Kumar R.Frequency estimation techniques for high dynamic trajectories[J].IEEE Transactions on Aerospace and Electronic Systems,1989,25(4):559-577.

[10]夏楠,邱天爽,等.一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法[J].电子学报,2013,41(1):148-152.

Xia Nan,Qiu Tian-shuang,et al.A nonlinear filtering algorithm combining the Kalman filter and the particle filter[J].Acta Electronica Sinica,2013,41(1):148-152.(in Chinese)

[11]刘望生,李亚安,王明环.复合K噪声下机动目标跟踪自适应UPF算法[J].电子学报,2012,40(6):1240-1245.

Liu Wang-sheng,Li Ya-an,Wang Ming-huan.An adaptive UPF algorithm for tracking maneuvering target in compound K noise environment[J].Acta Electronica Sinica,2012,40(06):1240-1245.

[12]Zhan R,Wan J.Iterated unscented Kalman filter for passive target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(3):1155-1163.

王伟(通信作者)男,1979年12月出生于安徽淮北,哈尔滨工程大学自动化学院教授,主要研究方向为卫星导航与捷联惯性导航.

E-mail:wangwei407@hrbeu.edu.cn

余玉揆男,1989年5月出生于江西抚州,哈尔滨工程大学自动化学院博士研究生.主要研究方向为非线性滤波,光纤非线性,光通讯信号处理.

E-mail:yykmaidou@gmail.com

郝燕玲女,1944年1月出生于山东省掖县,哈尔滨工程大学自动化学院教授,主要研究方向为组合导航技术、惯性导航及定位技术.

E-mail:ylhao@sina.com

A Novel Parallel Particle Filter for Frequency Estimation

WANG Wei,YU Yu-kui,HAO Yan-ling

(HarbinEngineeringUniversity,CollegeofAutomation,Harbin,Heilongjiang150001,China)

Abstract:To improve the tracking accuracy of the carrier frequency in low signal-to-noise ratio (SNR) and high dynamic environment,a new hybrid parallel particle filter algorithm,named multiple extend Kalman filter independent metropolis hastings (M-E-IMH) is presented.The proposed algorithm has a parallel structure and is verified to be more efficient for the real time implementation compared with particle filter (PF).The method utilizes the output of the in-phase and quadrature (IQ) branch as the observation directly to avoid the SNR loss caused by the discriminator.In both guass and non-guass environment,the simulations show that the proposed method has higher tracking accuracy at low SNR compared with the traditional methods,such as extended Kalman filter (EKF),particle filter (PF) and Kalman filter (KF) etc.

Key words:Doppler frequency estimation;parallel particle filter;high dynamic;non Gauss noise;real-time

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.036

中图分类号:TN966

文献标识码：A

文章编号：0372-2112 (2016)03-0740-07

基金项目：国家自然科学基金(No.61571148);中国博士后科学基金(No.2014M550182);黑龙江省博士后特别资助(No.LBH-TZ0410);哈尔滨市科技创新人才资助课题(No.2013RFXXJ016)

收稿日期:2014-06-25；修改日期：2015-05-20；责任编辑：梅志强