基于上下文信息和核熵成分分析的目标分类算法

潘　泓，朱亚平，夏思宇，金立左

(1.东南大学自动化学院，江苏南京 210096； 2.东南大学复杂工程系统测量与控制教育部重点实验室,江苏南京 210096；

3.中国传媒大学信息工程学院,北京 100024)



基于上下文信息和核熵成分分析的目标分类算法

潘泓1,2，朱亚平3，夏思宇1,2，金立左1,2

(1.东南大学自动化学院，江苏南京 210096； 2.东南大学复杂工程系统测量与控制教育部重点实验室,江苏南京 210096；

3.中国传媒大学信息工程学院,北京 100024)

摘要：结合图像属性上下文信息和核熵成分分析，构造了一种新颖的基于下上文信息的局部特征描述子——上下文核描述子(Context Kernel Descriptors,CKD).上下文信息的引入提高了CKD特征的鲁棒性，减少了特征误匹配.核熵成分分析从全维CKD特征分量中选出最能代表目标几何结构信息的特征分量，将其投影到这些特征分量张成的子空间上可得到降维CKD特征.在Caltech-101和CIFAR-10的测试结果表明，CKD的分类性能不仅明显优于其它局部特征描述子，还优于多数基于稀疏表示和深度学习等复杂模型的目标分类算法.

关键词:上下文核描述子；核熵成分分析；特征降维；目标分类

1引言

复杂环境中目标分类是模式识别和机器学习领域核心和极具挑战性的研究课题之一.实际应用中，目标在形状、尺寸、外观、颜色和姿态等方面的多样性，以及光照变化、复杂场景和局部遮挡的影响给目标分类带来了极大挑战.目前多数目标分类系统采用局部特征描述子结合部件模型表示目标物体，常用特征包括SIFT[1]、HOG[2]、KAZE[3]等方向直方图，LBP[4]、BSIF[5]、Shape Index Descriptor[6]等纹理直方图和Shape Context[7]、Binary Coherent Edge descriptors[8]等形状特征.

近年来，以核主成分分析(Kernel Principal Component Analysis,KPCA)[9]和支持向量机(Support Vector Machine,SVM)为代表的核空间特征分析和分类算法取得了极大成功.为此，人们将局部特征描述子和SVM技术结合起来，提出了多种局部匹配核函数[10～12]，将局部特征转换到高维核特征空间，并在核特征空间中匹配局部特征的相似性进行目标分类.此外，上下文信息的应用[13,14]有助于增强局部特征鉴别能力，提高目标分类算法性能.但目前提出的局部匹配核函数均未考虑上下文信息.如何将图像属性上下文信息与局部匹配核函数相结合，构造核空间上下文特征描述子；如何在保持核空间特征鉴别力的同时，尽可能降低特征维数是值得研究深入的问题.

结合上下文信息和核子空间分析技术，本文提出了一套基于核特征空间的目标分类框架.在特征提取阶段，将图像属性上下文信息融入核描述子(Kernel DEScriptors,KDES)[15]构造中，提出了一种新的基于上下文信息的局部特征描述子—上下文核描述子(CKD).上下文信息约束条件保持了特征描述子数值的空间连续性，提高了特征稳定性.在特征降维阶段，KDES采用KPCA进行特征降维.与KDES不同，我们采用基于核熵成分分析(Kernel Entropy Component Analysis,KECA)的特征降维方法，从所有特征分量中选出最能代表目标几何结构信息的特征分量，并将高维CKD投影到这些特征分量张成的子空间中得到低维鉴别力强的CKD，利用低维CKD特征训练SVM分类器进行目标分类.图1显示了本文提出的目标分类算法框架.本文方法特点在于该框架内所有模块(从特征提取、特征降维到分类)都在核特征空间内进行，克服了同一物体由于仿射变换、光照视角变化和局部被遮挡时导致局部特征长度不一，无法直接送入SVM进行分类的缺点.在Caltech-101和CIFAR-10数据集上测试结果表明，本文算法分类性能明显优于基于KDES、基于带监督KDES(Supervised Kernel DEScriptors,SKDES)[16]、基于稠密SIFT描述子[11]以及多数基于稀疏表示和深度学习的复杂目标分类模型.

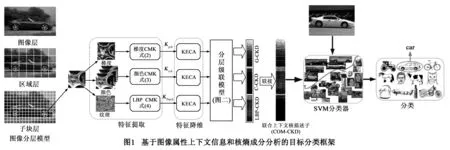
2基于CKD的特征提取

Bo等人研究[15]表明基于HOG和SIFT等方向直方图特征的图像块匹配过程等价于在相应图像块上定义某些特定的匹配核函数，并用匹配核函数比较图像块的相似性.基于此，他们提出了一种基于图像低层属性的广义局部特征描述子—核描述子(KDES).KDES在很多主流数据集上取得了良好的目标识别性能.KDES中，匹配核函数只考虑了像素点本身的属性，对不同上下文环境中具有相同属性的像素点进行子块特征匹配时易出现误匹配.为提高KDES特征匹配的鲁棒性，我们将像素点的邻域属性作为上下文信息融入匹配核函数构造过程中，提出上下文匹配核函数(Context Match Kernel,CMK)并构造上下文核描述子.我们认为如果两个图像块足够相似，那么其内部具有相似属性的像素点往往也应该具有相似属性的邻域元素.因此，将上述图像属性上下文约束条件引入匹配核函数中，能极大提高特征匹配的准确性.

2.1上下文匹配核函数(CMK)

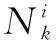
(1)

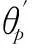
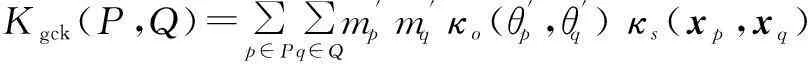
Kgck(P,Q)=∑p∈P∑q∈Qm'pm'qκo(θ'p,θ'q)κs(xp,xq)

(2)

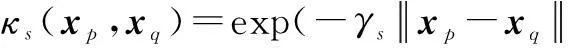
对图像颜色属性，我们可定义颜色上下文匹配核函数Kcck来比较P和Q子块的颜色相似性

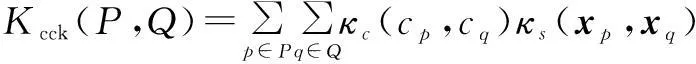
Kcck(P,Q)=∑p∈P∑q∈Qκc(cp,cq)κs(xp,xq)

·κcon[(xp,cp),(xq,cq)]

(3)

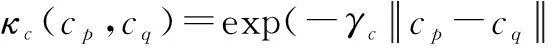
纹理属性也可用来比较不同图像子块间的相似性.我们采用局部二值模式(Local Binary Patterns,LBP)[4]作为纹理特征定义纹理上下文匹配核函数Klbpck

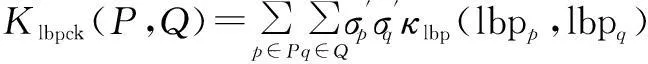
Klbpck(P,Q)=∑p∈P∑q∈Qσ'pσ'qκlbp(lbpp,lbpq)

·κs(xp,xq)κcon[(xp,lbpp),(xq,lbpq)]

(4)

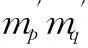
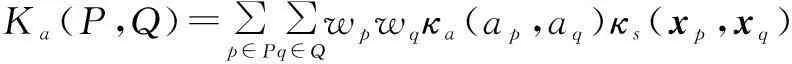
Ka(P,Q)=∑p∈P∑q∈Qwpwqκa(ap,aq)κs(xp,xq)

·κcon[(xp,ap),(xq,aq)]

(5)

式中，p和q分别表示图像子块P和Q中的像素点，wpwq和κa(·，·)分别对应线性归一化核函数和属性核函数.

2.2CKD的近似

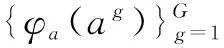
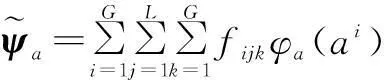
(6)

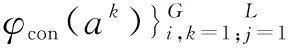
3基于KECA的特征降维

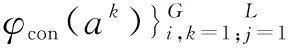
与KPCA不同的是，KECA[17]以信息论测度(Rényi熵)为标准，对核相似矩阵的特征向量进行排序，依次选出最大Rényi熵对应的特征向量作为主分量，这些主分量对应样本数据的高阶统计特性，反映了样本核特征空间角度分布特性[18].因此,KECA不仅最大程度保持了图像Rényi熵，而且很好地保持了图像几何拓扑结构.

3.1Rényi熵和KECA变换

若随机变量S的概率密度函数为p(s)，其二阶Rényi熵[19]H2(S)可定义为

H2(S)=-log2∫p2(s)ds

(7)

二阶Rényi熵具有很好的特性，是应用最多的Rényi熵.本文也用二阶Rényi熵作为特征选择和降维准则.为计算H2(S)，可用Parzen窗估计法[20]估计概率密度函数p(s).将式(7)表示为H2(S)=-log2[V(p)]，由于对数函数的单调性，只需考虑V(p).采用Parzen窗估计法，V(p)可以被估计为

(8)

k(s,st|σ)表示中心在st，窗宽为σ的Parzen窗核函数，K是Parzen窗对应的N×N核函数矩阵，1=[1,…,1]T是元素为1的N维列向量.

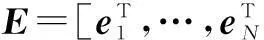
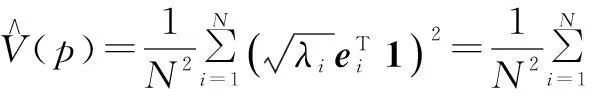
(9)

3.2分层联合CKD描述

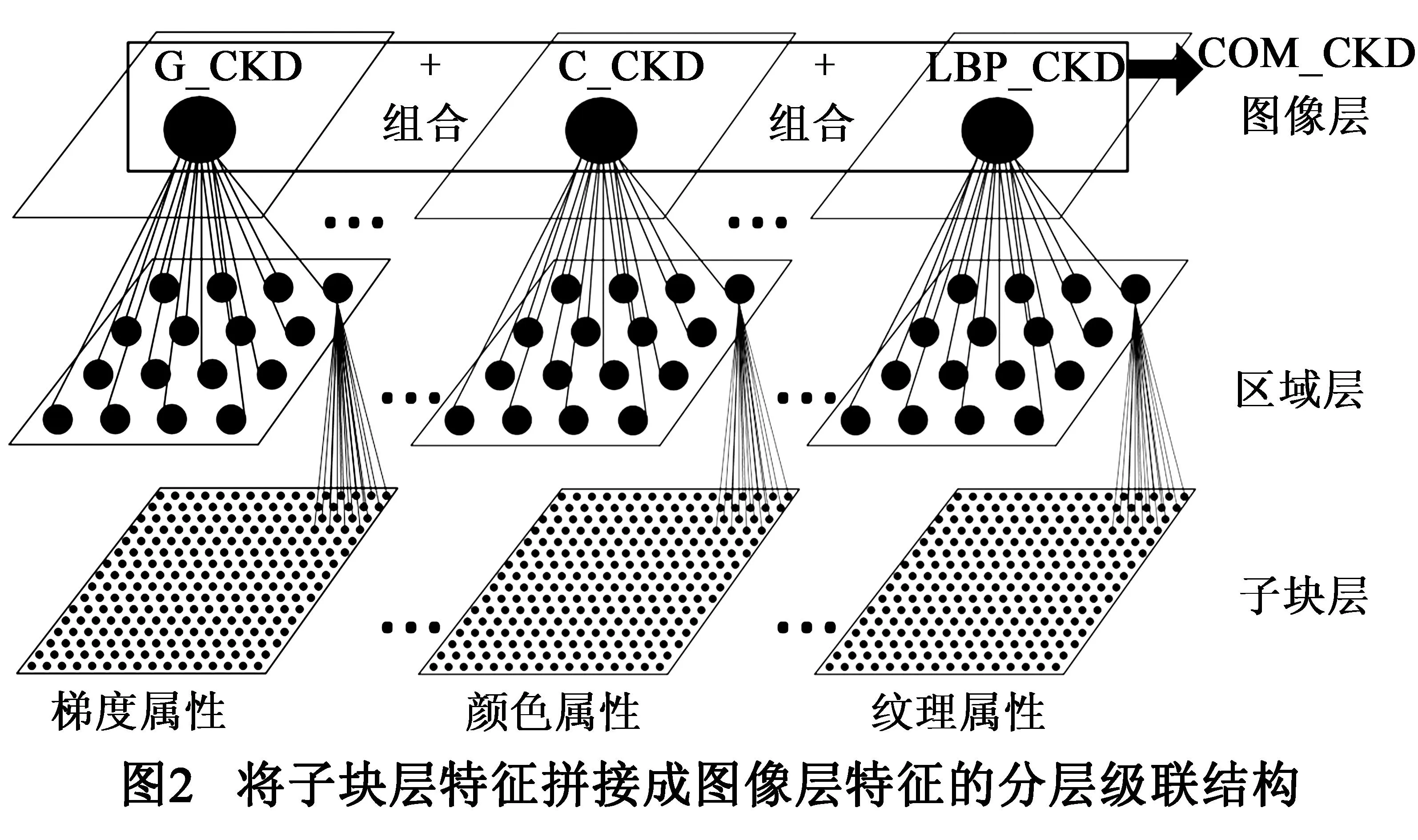
对式(2)～(4)定义的梯度、颜色和纹理CMK，分别对归一化相角、颜色、LBP算子和空间向量量化后生成有限个基函数，再利用KECA从基函数中选出最能描述样本类别几何结构的主分量张成子空间.将图像梯度、颜色、LBP算子、空间位置和上下文信息分别投影到KECA生成的子空间上，可得到降维后的梯度CKD(G-CKD)、颜色CKD(C-CKD)和纹理CKD(LBP-CKD).这些不同属性的CKD从不同角度描述图像子块，具有很好地互补性.为得到整个图像的CKD特征，对每种CKD采用图2所示的分层级联结构，逐层将相邻子块CKD拼接成区域CKD，再将相邻区域CKD拼接成图像层CKD.最后，将不同属性的图像层CKD组合在一起可以得到联合上下文核描述子(COM-CKD),COM-CKD提供了对整个图像丰富的、分层互补特征描述.

4实验结果

为保证比较的公平性，所有实验中除了特征维数以外，对CKD和KDES中的相同参数，都采用文献[15]的设置.所有核函数的窗宽γs,γo,γc和γlbp通过交叉验证方式确定.我们采用三层金字塔结构得到子块层(16×16 cell)、区域层(4×4 cell)和图像层(1×1 cell)特征描述.上下文核函数κcon中最优邻域参数k通过穷举搜索在k=1,…,8中确定.所有实验中用的分类器均为线性SVM分类器.

4.1Caltech-101数据集[21]的测试结果

对每类目标，选取30张图像作为训练样本，其余图像作为测试样本.对KDES和CKD描述子，训练一对多线性SVM分类器进行分类，整个分类过程一共进行5次，取5次分类平均值作为最后测试结果.SKDES的测试结果来自文献[16].表1比较了基于不同图像属性的KDES、SKDES和CKD描述子和一些近期算法对应的识别率均值和标准差.由表1可见，不论基于单个图像属性还是联合属性，CKD的识别率始终高于对应的KDES和SKDES.与KDES相比，除了G-CKD外，C-CKD和LBP-CKD识别率都显著高于对应的KDES.与SKDES相比，CKD识别率方差更小，这表明CKD比SKDES具有更稳定的识别性能.我们认为CKD构造时不仅考虑像素点本身的属性，还考虑其周围邻域像素的属性(上下文属性)，因而大大减少了不同目标图像子块中由于相似图像属性而引起的特征误匹配.其次，不论何种描述子，其联合属性识别率均高于单一属性识别率.这表明联合多种图像属性有助于提高特征鉴别能力和识别率.

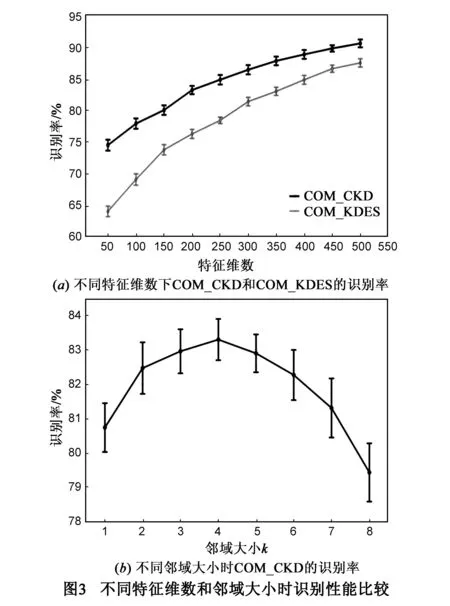
为比较特征维数对分类性能的影响，我们以联合CKD(COM-CKD)和联合KDES(COM-KDES)描述子为例，分别测试其在不同特征维数下的分类结果.图3(a)给出了两种描述子平均识别率和标准差随特征维数变化的情况.在所有特征维数下，不仅COM-CKD的识别率始终高于COM-KDES，而且随着特征维数下降，COM-CKD识别率的波动远小于COM-KDES.这表明COM-CKD描述子更能有效区分不同模式，即使在特征维数较低时依然有较稳定的鉴别能力.对COM-CKD描述子，我们将特征维数固定为200维，进一步研究邻域参数k对分类性能的影响.图3(b)比较了不同邻域大小时，COM-CKD分类性能的变化情况.由图3(b)可见，中等大小邻域(k=3,4,5)时，COM-CKD识别率最高，邻域过小(k=1,2)或太大(k=6,7,8)都会使COM-CKD分类性能下降.

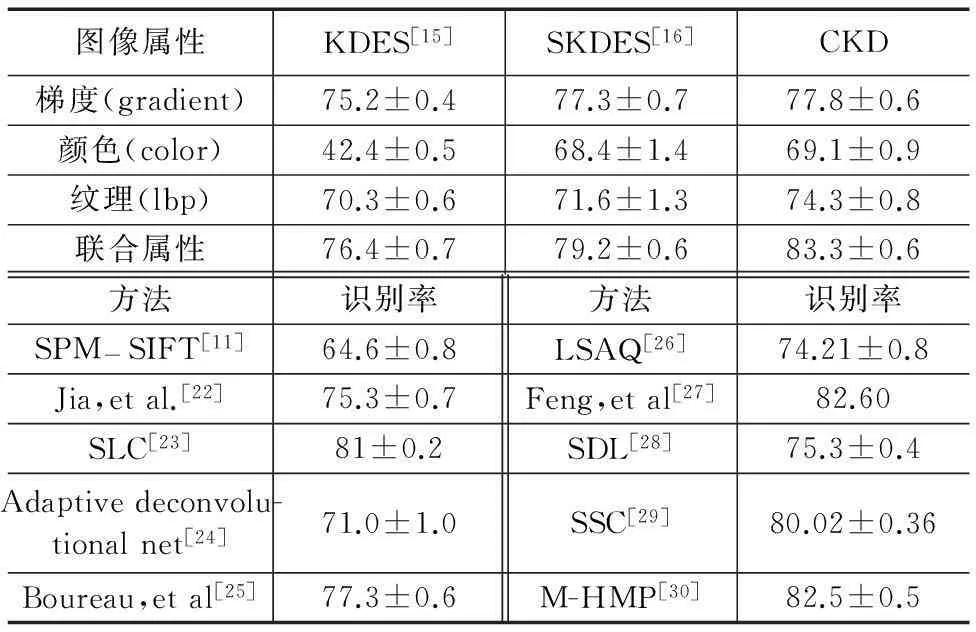
表1　KDES、SKDES、CKD和其它主流方法在Caltech-101数据集上

4.2CIFAR-10数据集的测试结果

CIFAR-10[31]是一个包含10类目标共60000张图像的大规模低分辨率图像数据集.每类目标含5000张训练图像和1000张测试图像，每张图像分辨率为32×32像素.由于图像分辨率较低，我们用间隔为2的网格对图像进行密集采样，对每个采样节点，以节点为中心选取周围8×8子块计算CKD.实验发现，CKD描述子邻域参数k=3时，对该数据集分类性能最佳.对每类目标，随机从5000张训练图像中取出1000张组成训练集，另外4000张组成验证集，通过交叉验证确定CKD中核函数参数γs,γo,γc和γlbp.

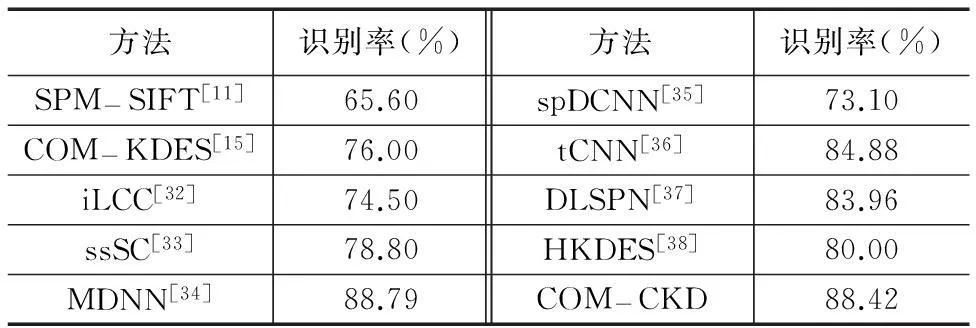
表2　各种算法在CIFAR-10上识别率的比较

我们将本文算法与目前主流的稀疏表示和深度学习方法进行比较.对比算法中，文献[32,33]属于稀疏表示方法；文献[34～37]为基于深度学习模型的方法.其他比较算法还包括SPM-SIFT(Spatial PyraMid dense SIFT)[11]和HKDES(Hierarchical Kernel DeScriptor)[38].表2列出了所有算法的分类准确率.由结果可见，COM-CKD和MDNN[34]的识别率高于其它算法.MDNN识别率比COM-CKD描述子高0.37%，但其复杂度远远高于本文算法.CKD描述子将图像属性映射到高维核特征空间，通过分层模型和特征组合得到具有较强鉴别力的特征描述子，即使配合简单线性SVM分类器，其分类性能也远好于spDCNN[35]、tCNN[36]等基于深度学习的复杂模型.从算法时间开销上看，在Intel Core i7 2.7GHz CPU和16GB RAM计算平台上，对一幅32×32像素的图像，本文算法计算200维COM-CKD(k=3)描述子共耗时244.84ms，其中图像属性量化和CKD描述子逼近用时224.63ms，KECA特征降维用时20.21ms.计算相同维数的COM-KDES描述子共耗时104.33ms，其中图像属性量化和KDES描述子逼近用时85.45ms，KPCA特征降维用时18.88ms.从算法复杂度上看，与KDES相比，本文算法的时间增加主要来源于在特征提取阶段，需要额外计算每个像素点的上下文核函数κcon.但上述计算量的增加均为线性.

5结论

本文提出了一种新颖的基于上下文信息的局部特征描述子——上下文核描述子.CKD的优点在于:(1)构造方便、计算简单，图像梯度、颜色、形状、纹理、边缘等属性均可用来构造CKD，采用分层级联结构可将子块特征转化为整个图像特征描述;(2)CKD定义中的上下文约束条件有效提高了描述子的稳定性，减少了特征误匹配;(3)KECA特征降维能有效提取反映样本类别几何结构信息的特征，使CKD更具特征鉴别力.实验结果表明，CKD描述子在主流数据集上的分类结果不仅明显优于KDES、SKDES和SIFT等局部特征描述子，还优于大多数基于稀疏表示和深度学习的复杂目标分类模型.

参考文献

[1]Lowe D.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.

[2]Dalal N,Triggs B.Histograms of oriented gradients for human detection[A].Schmid C.Proceedings of CVPR[C].San Diego,CA,USA:IEEE,2005.886-893.

[3]Alcantarilla P,Bartoli A,Davison A.KAZE features[A].Fitzgibbon A.Proceedings of ECCV[C].Florence,Italy:Springer,2012.214-227.

[4]Ojala T,Pietikäinen M,Mäenpää T.Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J].IEEE Trans,2002,PAMI-24(7):971-987.

[5]Kannala J,Rahtu E.BSIF:Binarized statistical image features[A].Proceedings of ICPR[C].Tsukuba,Japan:IEEE,2012.1363-1366.

[6]Pedersen K,Smidt K,Ziem A,et al.Shape index descriptors applied to texture-based galaxy analysis[A].Proceedings of ICCV[C],Sydney,NSW,Australia:IEEE,2013.2240-2447.

[7]Belongie S,Malik J,Puzicha J.Shape matching and object recognition using shape contexts[J].IEEE Trans,2002,PAMI-24(4):509-522.

[8]Zitnick C.Binary coherent edge descriptors[A].Daniilidis K.Proceedings of ECCV[C].Heraklion,Crete,Greece:Springer,2010.170-182.

[9]Scholkopf B,Smola A,Mulle K.Kernel principal component analysis[A].Gerstner W.Proceedings of ICANN[C].Lausanne,Switzerland:Springer,1997.583-588.

[10]Bo L,Sminchisescu C.Efficient match kernel between sets of features for visual recognition[A].Bengio Y.Proceedings of NIPS[C].Vancouver,Canada:NIPS,2009.135-143.

[11]Lazebnik S,Schmid C,Ponce J.Beyond bags of features:spatial pyramid matching for recognizing natural scene categories[A].Fitzgibbon A.Proceedings of CVPR[C].New York,NY,USA:IEEE,2006.2169-2178.

[12]Grauman K,Darrell T.The pyramid match kernel:Efficient learning with sets of features[J].JMLR,2007,8(4):725-760.

[13]Galleguillos C,Belongie S.Context based object categorization:A critical survey[J].Computer Vision and Image Understanding,2010,114(6):712-722.

[14]Myung J,Torralba A,Willsky A.Context models and out-of-context objects[J].Pattern Recognition Letters,2012,33(7):853-862.

[15]Bo L,Ren X,Fox D.Kernel descriptors for visual recognition[A].Lafferty J.Proceedings of NIPS[C].Vancouver,Canada:NIPS,2010.244-252.

[16]Wang P,Wang J,Zeng G,et al.Supervised kernel descriptors for visual recognition[A].Proceedings of CVPR[C].Portland,Oregon,USA:IEEE,2013.2858-2865.

[17]Jenssen R.Kernel entropy component analysis[J].IEEE Trans,2010,PAMI-32(5):847-860.

[18]Principe J.Information Theoretic Learning:Renyi’s Entropy and Kernel Perspectives[M].New York:Springer,2010.

[19]Rényi A.On measures of entropy and information[A].Neyman J.Fourth Berkeley Symposium on Mathematical Statistics and Probability[C].Berkeley,CA,USA:University of California Press,1961.547-561.

[20]Parzen E.On the estimation of a probability density function and the mode[J].The Annals of Mathematical Statistics,1962,33(3):1065-1076.

[21]Li F,Fergus R,Perona P.One-shot learning of object categories[J].IEEE Trans,2006,PAMI-28(4):594-611.

[22]Jia Y,Huang C,Darrell T.Beyond spatial pyramids:Receptive field learning for pooled image features[A].Proceedings of CVPR[C].Providence,Rhode Island,USA:IEEE,2012.3370-3377.

[23]McCann S Lowe D.Spatially local coding for object recognition[A].Lee M K.Proceedings of ACCV[C].Daejeon,Korea:Springer,2012.204-217.

[24]Zeiler M,Taylor W,Fergus R.Adaptive deconvolutional networks for mid and high level feature learning[A].Schiele B.Proceedings of ICCV[C].Barcelona,Spain:IEEE,2011.2018-2025.

[25]Boureau L,Roux L,Bach F,et al.Ask the locals:Multi-way local pooling for image recognition[A].Schiele B.Proceedings of ICCV[C].Barcelona,Spain:IEEE,2011.2651-2658.

[26]Liu L,Wang L,Liu X.In defense of soft-assignment coding[A].Schiele B.Proceedings of ICCV[C].Barcelona,Spain:IEEE,2011.2486-2493.

[27]Feng J,Ni B,Tian Q,et al.Geometriclp-norm feature pooling for image classification[A].Proceedings of CVPR[C].Colorado Springs,USA:IEEE,2011.2697-2704.

[28]Jiang Z,Zhang G,Davis S.Submodular dictionary learning for sparse coding[A].Proceedings of CVPR[C].Providence,Rhode Island,USA:IEEE,2012.3418-3425.

[29]Oliveira G,Nascimento E,Vieira A.Sparse spatial coding:a novel approach for efficient and accurate object recognition[A]. Proceedings of ICRA[C].St Paul,MN,USA:IEEE,2012.2592-2598.

[30]Bo L,Ren X,Fox D.Multipath sparse coding using hierarchical matching pursuit[A].Proceedings of CVPR[C].Portland,Oregon,USA:IEEE,2013.660-667.

[31]Torralba A,Fergus R,Freeman W.80 million tiny images:A large data set for nonparametric object and scene recognition[J].IEEE Trans,2008,PAMI-30(11):1958-1970.

[32]Yu K,Zhang T.Improved local coordinate coding using local tangents[A].Proceedings of ICML[C].Haifa,Israel:Omnipress,2010.1215-1222.

[33]Goodfellow I,Courville A,Bengio Y.Spike-and-Slab sparse coding for unsupervised feature discovery[A].NIPS Workshop on Challenges in Learning Hierarchical Models[C].Granada,Spain:NIPS,2011.

[34]Ciresan D,Meier U Schmidhuber J.Multi-columndeep neural networks for image classification[A].Proceedings of CVPR[C].Providence,Rhode Island,USA:IEEE,2012.3642-3649.

[35]Zeiler M,Fergus R.Stochastic pooling for regularization of deep convolutional neural networks[A].Goodfellow I.Proceedings of ICLR[C].Scottsdale,Arizona,USA:IEEE,2013.

[36]Le Q,Ngiam J,Chia C,et al.Tiled convolutional neural networks[A].Lafferty J.Proceedings of NIPS[C].Vancouver,Canada:NIPS,2010.1279-1287.

[37]Gens R,Domingos P.Discriminative learning of sum-product networks[A].Pereira F.Proceedings of NIPS[C].Lake Tahoe,Nevada,USA:NIPS,2012.1-9.

[38]Bo L,Lai K,Ren X,et al.Object recognition with hierarchical kernel descriptors[A].Proceedings of CVPR[C].Colorado Springs,USA:IEEE,2011.1729-1736.

潘泓(通信作者)男，1974年生于江苏.现为东南大学自动化学院副教授.主要研究方向为机器学习,模式识别，特征提取与选择，目标分类与检测，计算机视觉.

E-mail:enhpan@seu.edu.cn

朱亚平女,1977年生于河南.现为中国传媒大学信息工程学院教授.主要研究方向为图像处理和机器学习.

E-mail:zhuyaping@cuc.edu.cn

夏思宇男，1978年生于湖北.现为东南大学自动化学院副教授.主要研究方向为机器学习，模式识别，社交媒体分析等.

E-mail:xsy@seu.edu.cn

金立左男，1972年生于江苏.现为东南大学自动化学院副教授.主要研究方向机器视觉、模式识别、机器学习、信息融合与嵌入式系统.

E-mail:jinlizuo@gmail.com

Object Classification Using Context Cue and Kernel Entropy Component Analysis

PAN Hong1，2,ZHU Ya-ping3,XIA Si-yu1，2,JIN Li-zuo1，2

(1.SchoolofAutomation,SoutheastUniversity,Nanjing,Jiangsu210096,China;2.KeyLaboratoryofMeasurementandControlofCSE,MinistryofEducation,SoutheastUniversity,Nanjing,Jiangsu210096,China;3.SchoolofInformationEngineering,CommunicationUniversityofChina,Beijing100024,China)

Abstract:Combining the context cue of image attributes and kernel entropy component analysis (KECA),we proposed a context-based local feature descriptor called context kernel descriptors (CKD).Context cue implied in the CKD improves its robustness,thus reducing false matches during feature correspondence.KECA applied in the feature dimensionality reduction step selects the principal eigenvectors that contribute most to the geometrical structure of input images.Projecting the full-dimensional CKD onto the subspaces spanned by these principal eigenvectors,we derive the final low-dimensional CKD.Evaluation results on Caltech-101 and CIFAR-10 show that the classification performance of the proposed CKD significantly outperforms other local descriptors,and even surpasses most sparse representation-based and deep learning-based sophisticated object classification methods.

Key words:context kernel descriptors;kernel entropy component analysis;feature reduction;object classification

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.013

中图分类号:TP391

文献标识码：A

文章编号：0372-2112 (2016)03-0580-07

基金项目:国家自然科学基金(No.61101165);江苏省自然科学基金(No.BK20131296,No.BK20130639);航空科学基金(No.20115169016);国家科技支撑计划课题(No.2012BAH02B03)

收稿日期:2014-07-18;修回日期:2014-11-21；责任编辑：覃怀银