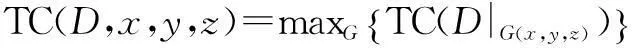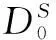三元变量间一维流形依赖关系的检测

李玉鑑,张亚红

(北京工业大学计算机学院,北京 100124)



三元变量间一维流形依赖关系的检测

李玉鑑,张亚红

(北京工业大学计算机学院,北京 100124)

摘要：最大信息系数(Maximum Information Coefficient,MIC)能够很好的检测成对变量间的线性和非线性依赖关系，但却不能直接用于检测三元变量间的相关关系.基于MIC的思想和全相关的概念，本文提出了一种直接检测三元变量间一维流形依赖关系的方法—最大全相关系数(Maximal Total Correlation Coefficient,MTCC).MTCC用落在[0,1]区间上的值来表明三元变量间一维流形依赖关系的强弱，其中0和1分别表示最弱和最强的依赖关系.使用MIC的计算策略，本文还提出了一种有效的动态规划方法来近似计算MTCC的值.仿真实验说明MTCC与非线性相关信息熵(Nonlinear Correlation Information Entropy,NCIE)相比具有更好的通用性和公平性，真实数据的分析验证了MTCC的实用性.最后，强调了其专用性.

关键词:数据挖掘；三元相关；一维流形依赖；最大信息系数；最大全相关系数；非线性相关信息熵

1引言

近年来，由于在基因组学、物理学、政治科学、经济学等众多领域出现了越来越多的大规模数据集，因此如何检测大数据中潜在的依赖关系受到了人们日益广泛的关注[1,2].检测依赖关系的主要目的是发现大数据集中成对变量间的重要相关关系，其中相关关系可以是任意的线性或非线性函数关系、以及更为复杂的统计依赖关系.如果数据集中包含几百、甚至几千个以上的变量，那么用人工方法一一检测这些变量之间的依赖关系是不现实的.

迄今为止，研究者们已经提出了许多用于检测数据变量依赖关系的方法，如互信息估计[3～5]、最大相关[6,7]、基于主曲线的方法[8～11]、距离相关[12,13]、Pearson相关系数和Spearman秩相关等等.以互信息为基础， Reshef等人[1]于2011年在国际上最顶级的期刊Science上发表论文，引入了最大信息系数(Maximal Information Coefficient,MIC)的概念，用于检测大数据集中的相关关系.MIC可能是世界上目前最好的相关性检测方法，被称为一种21世纪的相关性[14].与其它方法相比，最大信息系数MIC通常具有更好的通用性和公平性，也就是说，利用MIC不仅能够检测更为广泛的关系类型，而且在同等噪声条件下，不同关系类型的MIC值彼此更为接近.虽然MIC的公平性受到质疑[15]，但经过学术争论后又得到了进一步的确认[16].正是由于这些优点，MIC获得了大量成功的应用.比如，将MIC应用于世界卫生数据、棒球统计数据、酵母菌基因表达数据和人类肠道的细菌丰度数据，确实帮助发现了许多已知和新颖的相关关系[1].此外， MIC还被应用于基因组学[17]，蛋白质组学[18]，微生物学[19]，以及传感器[20]等领域.

然而，以上介绍的相关性分析方法，包括MIC，都不能直接检测三元(多元)变量间的相关关系.事实上，目前涉及三元(多元)变量间相关性的研究还比较少，本文在分析相关工作时只找到了一种方法，即非线性相关信息熵(Nonlinear Correlation Information Entropy,简称NCIE)[21].NCIE是一种检测多元变量依赖关系的非参数方法，可以通过用两两变量估计的互信息矩阵来计算，能够用0～1之间的取值表示三元变量数据集的依赖关系强弱.NCIE的主要缺点是只有在三个变量完全相同的情况下才能取值1，对许多常见的空间曲线取值明显小于1，因此不具有良好的通用性.而且，NCIE也不具有良好的公平性，因为对不同类型的依赖关系相同的NCIE值对应的噪声水平一般差别较大.

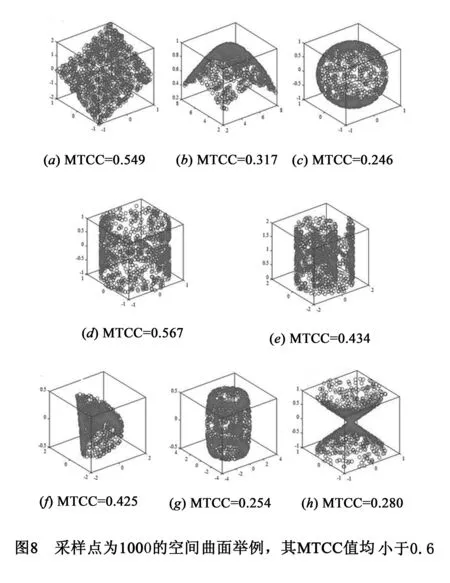
本文将利用MIC的通用性和公平性优点，将其扩展为一种新的统计分析工具，即最大全相关系数(Maximal Total Correlation Coefficient,MTCC)，用于直接检测三元变量间一维流形依赖关系.由于MTCC和MIC具有共同的信息理论基础，所以MTCC能够在一定程度上继承MIC的通用性和公平性.本文将通过三维空间曲线上的仿真实验说明MTCC能够有效的检测三元变量间一维流形依赖关系，同时在与NCIE比较的基础上验证其通用性和公平性.此外，我们还将MTCC应用于分析全球健康和棒球联盟数据，进一步评价其分析真实数据的有效性和可行性.最后，本文通过三维空间曲面上的仿真实验指出了MTCC的固有缺点，这虽然说明MTCC还不足以有效地检测三元变量间二维流形依赖关系，但同时也说明它具有良好的专用性，即可以被看作一种检测三元变量间一维流形依赖关系的专用方法，能够给出比较可靠的检测结果.

2最大全相关系数(MTCC)

本节在简介MIC的基础上，给出MTCC的严格定义和计算方法.

2.1MIC简介

MIC的基础是二元随机变量X和Y之间的互信息.如果用H(·)表示为信息熵，那么X和Y的互信息定义为：I(X,Y)=H(X)+H(Y)-H(X,Y).

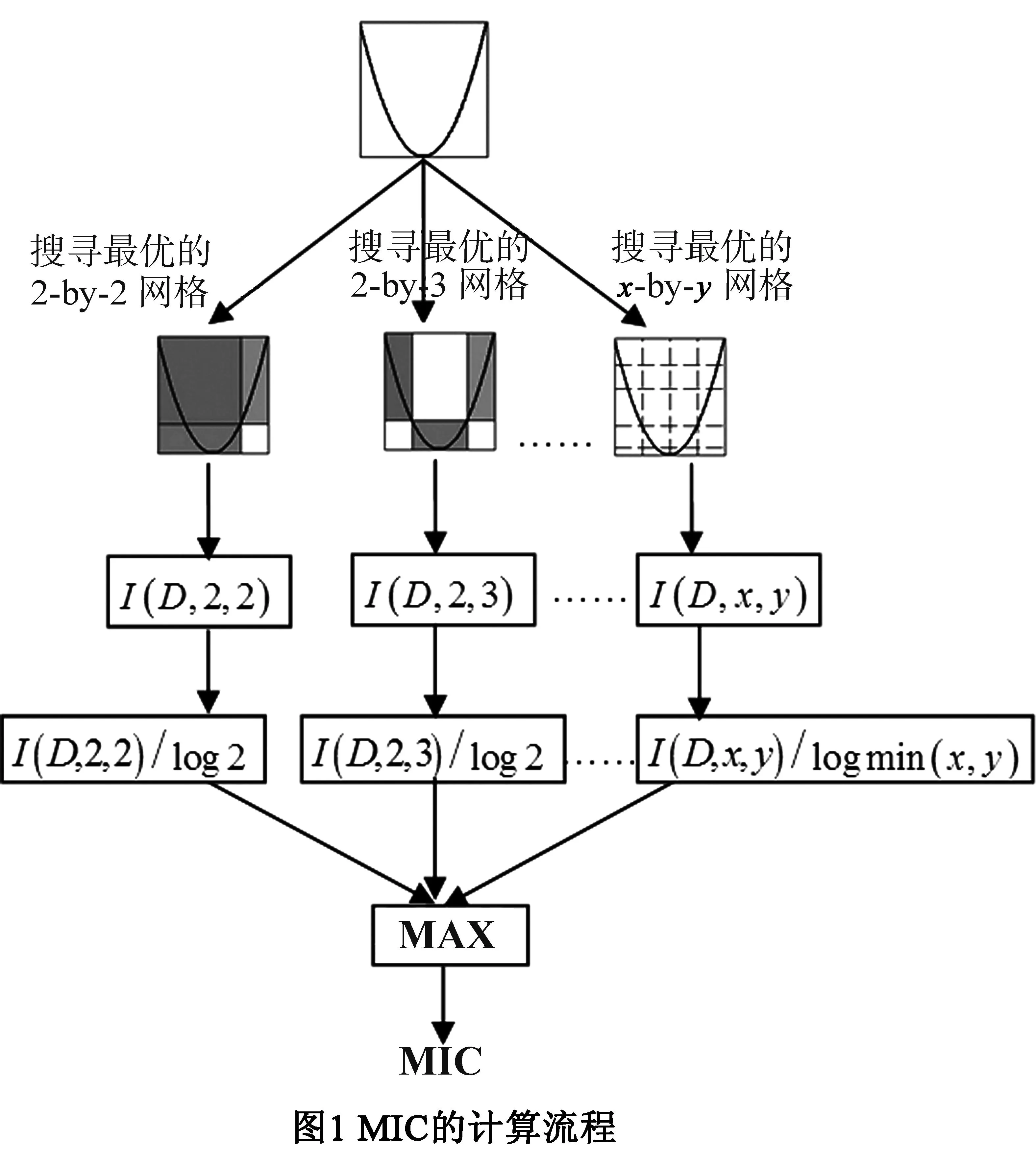
MIC的基本思想是：如果变量X和Y之间存在某种相关关系，那么在它们的散点图上就应该能够构造一个特殊的网格，使得数据点在该网格上的互信息明显大于0.MIC就是通过具有最大归一化互信息的网格来定义的，并由此评估变量依赖关系的强弱.

给定有限二元数据集D，任意划分x行和y列，就可以得到一个x-by-y的2维网格G(x,y)，其中允许某些行或列包含的数据点为空，而且网格线的间距可以不相等.D|G为集合D在G上的概率分布，其中数据点落在每个格子的概率是该格子内所包含的样本点数量占全体样本点的比例.如果用I(D|G)表示网格G在D上产生的互信息，用I(D,x,y)表示所有大小为x-by-y的网格G(x,y)在D上产生的最大互信息，那么I(D,x,y)=maxG{I(D|G(x,y))}.据此，可以把数据集D的最大信息系数定义为：

(1)

其中B=nα(0<α<1)，计算时取经验值B=n0.6用于控制网格的大小上限.

MIC的计算流程如图1所示.需要指出的是，对每个给定的x和y，搜索产生理论上最大互信息的网格G是非常耗时的计算过程，因此在应用时需要采用一种基于动态规划的方法近似处理，详见文献[1].

2.2MTCC的定义

前面已经指出，MIC以两元随机变量间的互信息为基础，而最大全相关系数MTCC则以三元随机变量间的全相关为基础.在信息理论中，全相关可以看作是互信息的一种推广，能够定量地表达n个随机变量间依赖关系的强弱.全相关在n=2时退化为互信息.任意三个随机变量(X,Y,Z)的全相关可定义如下：

TC(X;Y;Z)=H(X)+H(Y)+H(Z)-H(X,Y,Z)

(2)

从直观上说，MTCC是MIC从两维平面到三维空间的一种推广，即从两元变量间的一维流形依赖推广到三元变量间的一维流形依赖.与MIC的主要区别在于，MTCC是用3维网格代替2维网格来定义的，通过搜索具有最大归一化全相关的网格来评估三元变量依赖关系的强弱.

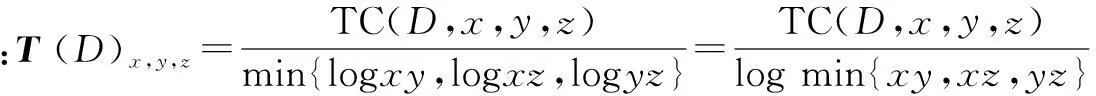
根据概率论，0≤TC(D,x,y,z)≤log min{xy,xz,yz}，因此0≤T(D)x,y,z≤1，从而0≤MTCC(D)≤1.这意味着最大全相关系数MTCC的取值恒在0和1之间.MTCC=0表示三个变量完全独立，此时依赖关系最弱.MTCC=1表示三个变量完全相互依赖，此时依赖关系最强.

2.3MTCC的计算方法

根据MTCC的定义，参照MIC的计算流程，对给定三元变量数据集D，计算其最大全相关系数MTCC的过程可归纳为以下5个步骤：

步骤1对于任意三个均大于1的正整数x,y,z，如果xyz

步骤2统计每个格子所包含D的样本点数，在G上诱导出概率分布p(x,y,z)、p(x)、p(y)和p(z).其中，p(x,y,z)表示在第(x,y,z)个格子中包含的样本点数占全体样本点的比例，p(x)、p(y)和p(z)分别表示x-轴、y-轴和z-轴上的边际分布；

步骤4计算特征张量元素T(D)x,y,z，构造特征张量T(D)；

图3给出了一些特征张量的可视化结果.不难看出，对不同类型的一维流形依赖关系而言，相应的特征张量通常是不同的.

3实验结果与分析

本节通过实验讨论MTCC的通用性、公平性、实用性和专用性.

3.1通用性和公平性实验

由图2不难看出，在无噪声的情况下，对于三元变量间的许多线性和非线性一维流形依赖关系，它们的MTCC值都为1，而非线性相关信息熵NCIE的值却几乎不为1.对于NCIE来说，三元变量间的无噪线性依赖关系的强度要明显大于无噪非线性依赖关系的强度，而事实上它们的强度应该大体相同才是合理的.因此，与NCIE相比，MTCC具有更好的通用性.

图5是采用类似图4的方法构造带噪声的数据集，但只列举了MTCC=0.80,0.65,0.50,0.35的情况.从中不难看出，随着噪声水平的增加，虽然MTCC将逐步减小，但只要噪声水平大致相同，不同类型依赖关系的MTCC值也是彼此接近的.

3.2实用性实验

为了说明MTCC在分析实际数据时检测三元变量间一维流形依赖关系的实用性，本文利用世界健康卫生数据(WHO)和美国职业棒球联盟数据(MLB)进行了两组应用实验.WHO包含世界卫生组织及其合作伙伴[22,23]所提供的社会，经济，健康和政治指标等数据，MLB包含2008年美国职业棒球大联盟赛季[24,25]的性能统计数据.这两个数据集的二元依赖关系已经用MIC分析过[1]，这里我们主要应用MTCC在类似的统计显著性条件下分析其中三元变量间的一维流形依赖关系.

在WHO上做分析时，我们只选择了其中的一个子集，由43个变量构成.这43个变量是文献[1]的表S9提供的，共包含12341个三元组.图6(a)是实验得到的MTCC直方图结果，其中MTCC值大于0.7的三元组共有758个，占6.14%.图6(b)～(h)给出了若干根据MTCC值挑选的依赖关系，图中拟合曲线由手工选择回归函数产生，较好地反映了数据的变化趋势.值得注意的是，图6(d)包含两条趋势线，一条是少数点趋势线，主要由一组科技产业高度发达的国家组成，其人均电脑较多、电力消耗和人均能源消耗较大，另一条是多数点趋势线，由其它国家组成，其电力消耗和人均能源消耗随着人均电脑数大致均匀地增加.此外，图6(e)包含3条趋势线，反映了“5岁以下儿童死亡率”，“人均健康投入”和“人均收入”这3个变量在不同条件下存在的三种依赖关系，从中不难看出，通过增加“人均收入”或者“人均健康投入”，都有助于降低“5岁以下儿童的死亡率”，因此可望指导决策者制定相应的全民健康政策.图6(i)中没有明显的变量依赖关系，所以MTCC值较小，只有0.167.

在MLB上做分析时，我们也只选择了其中的一个子集，由50个变量构成.这50个变量是文献[1]的表S12提供的，共包含196000个三元组.图7(a)是实验得到的MTCC直方图，其中MTCC值大于等于0.7的三元组共有3929个，占20%.图7(b)～(h)给出了若干根据MTCC值挑选的依赖关系，其中反映数据变化趋势的拟合曲线也是由手工产生的.值得注意的是，图7(f)包含两条趋势线，反映了“games played as a pinch hitter (G-PH)”，“plate appearances as a pinch hitter (PA-PH)”和“true runs tells of a player′s total offensive contribution in runs (EqR)”这三个变量之间在不同条件下可能存在的两种依赖关系，其具体含义留给棒球爱好者来阐明.

3.3MTCC的专用性实验

通过上述分析，MTCC在用来检测三元变量间的一维流形依赖关系时无疑是非常成功的.但它并不是万能的，也有其固有缺陷.比如，MTCC在检测三元变量间的二维流形依赖关系时，还不能被看作一种理想的方法.事实上，针对图8所示的无噪空间曲面，MTCC的值虽然不算太小，但一般也小于0.6.当然，这同时也进一步说明，MTCC可以看作是一种检测三元变量间一维流形依赖关系的专用方法，具有较高的可靠性.

4结论

本文通过推广最大信息系数MIC，提出了最大全相关系数MTCC的概念.MTCC可以用来直接检测三元变量间一维流形依赖关系，并较好地继承了MIC的通用性和公平性.通过将MTCC应用于分析世界健康卫生数据和美国职业棒球联盟数据，本文还进一步验证了其实用性，有助于确认或揭示数据中三元一维流形依赖关系.虽然MTCC不能有效的检测三元二维流形依赖关系，但这又说明了它的专用性，因此在检测三元一维流形依赖关系方面给出的结果具有良好的可靠性.

由于MIC在检测二元变量间的依赖关系方面已经被公认为是一种重要的工具和方法[15]，所以MTCC作为MIC的推广，MTCC可以看作是MIC的一大进步.与MIC相比，MTCC有时可以揭示更多的信息内容，因此像MIC一样，MTCC也将在分析各个不同科学领域的复杂数据时获得越来越多的应用.

参考文献

[1]Reshef D N,Reshef Y A,Finucane H K,et al.Detecting novel associations in large data set[J].Science,2011,334 (6062):1518-1524.

[2]Staff S.Challenges and opportunities[J].Science,2011,331(6018):692-693.

[3]Venelli A.Efficient Entropy Estimation for Mutual Information Analysis Using B-splines[M].Heidelberg,Berlin,Germany:Springer Berlin Heidelberg,2010.17-30.

[4]Khan S,Bandyopadhyay S,Ganguly A R,et al.Relative performance of mutual information estimation methods for quantifying the dependence among short and noisy data[J].Physical Review E,2007,76(2):62-85.

[5]Kraskov A,Støgbauer H,Grassberger P.Estimating mutual information[J].Physical Review E,2004,69(6):279-307.

[6]Yu Y.On the maximal correlation coefficient[J].Statistics & Probability Letters,2008,78(9):1072-1075.

[7]Zhang L H,Liao L Z,Sun L M.Towards the global solution of the maximal correlation problem[J].Journal of Global Optimization,2011,49(1):91-107.

[8]苏菡，黄凤岗.一种基于主曲线的步态识别方法[J].电子学报,2007,35(9):1685-1690.

Su H,Huang F G.An automatic human gait recognition based on principle curves[J].Acta Electronica Sinica,2007,35(9):1685-1690.(in Chinese)

[9]Hongyun Z,Duoqian M,Dongxing Z.Analysis and extraction of structural features of off-line handwritten digits based on principal curves[J].Journal of Computer Research and Development,2005,42(8):1344-1349.

[10]Verbeek J J,Vlassis N,Krøse B.A k-segments algorithm for finding principal curves[J].Pattern Recognition Letters,2002,23(8):1009-1017.

[11]Delicado P,Smrekar M.Measuring non-learning dependence for two random variables distributed along a curve[J].Statistics and Computing,2009,19(3):255-269.

[12]Székely G J,Rizzo M L,Bakirov N K.Measuring and testing dependence by correlation of distances[J].The Annals of Statistics,2007,35(6):2769-2794.

[13]Székely G J,Rizzo M L.Brownian distance covariance[J].The Annals of Applied Statistics,2009,3(4):1236-1265.

[14]Speed T.A correlation for the 21st century[J].Science,2011,334(6062):1502-1503.

[15]Kinney J B,Atwal G S.Equitability,mutual information,and the maximal information coefficient[J].Proceedings of the National Academy of Sciences,2014,111(9):3354-3359.

[16]Reshef D N,Reshef Y A,Mitzenmacher M,et al.Cleaning up the record on the maximal information coefficient and equitability[J].Proceedings of the National Academy of Sciences,2014,111(33):E3362-E3363.

[17]Das J,Mohammed J,Yu H.Genome-scale analysis of interaction dynamics reveals organization of biological networks[J].Bioinformatics,2012,28(14):1873-1878.

[18]Pang C N I,Goel A,Li S S,Wilkins M R.A multi-dimensional matrix for systems biology research and its application to interaction networks[J].Journal of Proteome Research,2012,11(11):5204-5220.

[19]Koren O,Goodrich J K,Cullender T C,et al.Host remodeling of the gut microbiome and metabolic changes during pregnancy[J].Cell,2012,150(3):470-480.

[20]Sagl G,Blaschke T,Beinat E,et al.Ubiquitous geo-sensing for context-aware analysis:exploring relationships between environmental and human dynamics[J].Sensors,2012,12(7):9800-9822.

[21]Wang Q,Shen Y,Zhang J Q.A nonlinear correlation measure for multivariable data set[J].Physica D,2005,200(3-4):287-295.

[22]World-Health-Organization.World Health Organization Statistical Information Systems (whosis)[DB/OL],http://www.who.int/whosis/en/,2009.

[23]Rosling H.Indicators in Gapminder World[DB/OL].http://www.gapminder.org/data/,2009.

[24]Baseball Prospectus Statistics Reports[DB/OL].http://www.baseballpropectus.com/sortable/,2009.

[25]Lahman S.The Baseball Archive[DB/OL].http://baseball1.com/statistics/,2009.

李玉鑑男，1968年生于广西省，1999在中国科学院半导体研究所获得博士学位，现为北京工业大学计算机学院教授.主要研究方向为模式识别与机器学习，图像处理，深度学习等.

E-mail:liyujian@bjut.edu.cn

张亚红女，1987年生于河南省,2011年获得河南理工大学计算机系学士学位，现为北京工业大学计算机学院博士.主要研究方向为模式识别与机器学习.

E-mail:plahpu@163.com

A Detecting Measure for Trivariate One-Dimensional Manifold Dependences

LI Yu-jian,ZHANG Ya-hong

(CollegeofComputerScienceandTechnology,BeijingUniversityofTechnology,Beijing100124,China)

Abstract:Maximal information coefficient (MIC) is a good measure for detecting linear and nonlinear correlation between pairs of variables,but not directly applicable for triplets.Based on the idea of MIC and concept of total correlation,we propose the maximal total correlation coefficient (MTCC),which measures a one-dimensional manifold dependence among three variables with a score in [0,1],where 0 stands for the weakest and 1 for the strongest.Using the strategy of computing MIC,we also present an efficient dynamic programming method to approximate the true value of MTCC in practice.Simulation results show that MTCC has better generality and better equitability than nonlinear correlation information entropy (NCIE).By analyzing real datasets,we further verify the feasibility of MTCC.Finally,we emphasize its specificity.

Key words:data mining;trivariate correlation;one-dimensional manifold dependence;maximal information coefficient;maximal total correlation coefficient;nonlinear correlation information entropy

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.022

中图分类号:TP391

文献标识码：A

文章编号：0372-2112 (2016)03-0639-07

基金项目:国家自然科学基金(No.61175004);北京市自然科学基金(No.4112009);高等学校博士学科点专项科研基金(No.20121103110029)

收稿日期:2014-07-07；修回日期：2015-03-09；责任编辑：梅志强