圆周SAR子孔径频域成像处理方法研究

贾高伟,常文革

(国防科技大学电子科学与工程学院，湖南长沙 410073)



圆周SAR子孔径频域成像处理方法研究

贾高伟,常文革

(国防科技大学电子科学与工程学院，湖南长沙 410073)

摘要：圆周合成孔径雷达(Circular Synthetic Aperture Radar,CSAR)因具有超高分辨率、三维成像能力、全方位信息获取等优势已经成为雷达领域的研究热点.在实际应用中，场景中目标通常仅在较小观测角度内具有近似恒定的散射特性.为此本文提出了一种基于子孔径划分的CSAR频域成像处理方法，该方法相比于时域成像处理具有更高的处理效率.文中给出了CSAR回波的频谱表达形式并深入分析了其特性；提出了CSAR子孔径频域成像处理的基本流程，理论上详细论证了文中所提算法的可行性.最后仿真试验证实了文中所提信号模型及成像处理流程的正确性.

关键词:圆周合成孔径雷达；频域成像处理；子孔径处理

1引言

圆周合成孔径雷达(Circular Synthetic Aperture Radar,CSAR)具有二维超高分辨力、三维成像、全方位角信息获取等突出优势[1～5]，已成为SAR领域的研究热点.目前，美国空军实验室，瑞典防务研究院，法国宇航局，德国宇航中心及中国科学院电子所的研究学者已开展了CSAR的机载试验，初步验证了其独特优势[6,7].

已有的CSAR外场试验表明[5]，在观测区域内，绝大多数目标仅在较小的观测范围内具有近似恒定的电磁散射特性.尤其对于高波段SAR(如X波段)，目标电磁散射特性对电磁波方位入射角十分敏感.此时单航过CSAR成像的优势体现在对目标散射特性的全方位获取，而二维超高分辨、三维成像能力则受到限制.更重要的是，对于待观测目标，若雷达回波相参积累角大于目标散射主波束宽度，相参成像处理会引入大量噪声进而使得目标的点散布函数出现强副瓣特性.因此在实际应用过程中没有必要对CSAR回波进行360°范围内的相参积累.

目前，CSAR的成像处理仍不成熟.在机载试验中广泛采用的是后向投影算法(Back-Projection，BP)及其改进型快速BP算法[6].BP算法对雷达理想轨迹的依赖性低，但需要精确获知雷达轨迹参数，且其计算量很大.频域成像处理方面，CSAR运行路径的严重非线性导致传统的适用于线性轨迹SAR的成像方法[8,9]均已不再适合.Soumekh在文献[1]中提出了基于格林函数傅里叶分析的CSAR成像算法，其他一些学者也提出了不同的频域处理算法[3,4,10]，但总体而言频域算法的研究仍不充分，表现在此类成像算法仅对场景中心点及其附近较小区域有效，且不易量化分析算法中近似处理对成像结果的影响.

本文的研究集中于利用单航过CSAR数据在频域完成对平坦场景进行二维成像处理.

2CSAR信号频谱分析

CSAR的成像几何模型如图1所示.图1(a)中，雷达沿半径为R的圆周运动，方位向观测角为θ，雷达天线相位中心(Array Phase Center,APC)的三维坐标为(xr,yr,H)，极坐标为(Rcosθ,Rsinθ,H).在雷达运动过程中其波束始终指向半径为Ra的成像区域，设定成像区域为水平地面.设非中心点目标P的坐标为(x,y,0)，其极坐标为(rcosφ,rsinφ,0)，O为坐标原点.图1(b)表示雷达成像几何的侧视图，θz为雷达相对场景中心点的俯视角.直观地，可以得到APC同目标P之间的瞬时斜距Rr为：

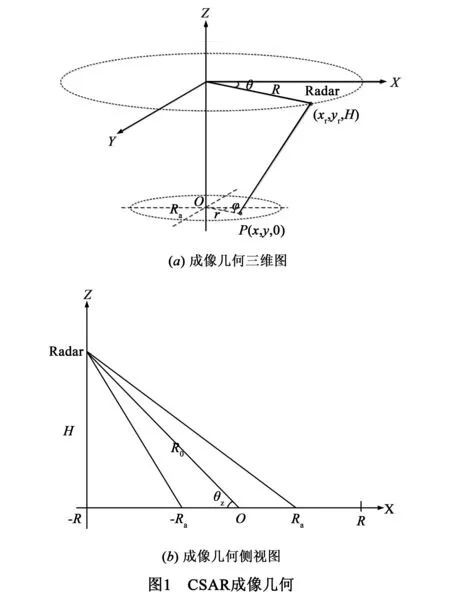
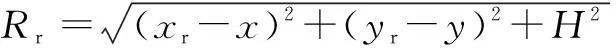
Rr=(xr-x)2+(yr-y)2+H2

(1)

设雷达发射信号为线性调频信号(Linear Frequency Modulation,LFM):

(2)

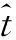
(3)

k=2π(fc+f)/c表示距离向波数，f为距离向频率.沿方位观测角θ进行傅里叶变换，可以得到：

S(k,ξ)=∫exp(-j2kRr)exp(-jξθ)dθ

(4)

ξ为角度域波数.针对式(4)，基于驻定相位原理[8]可以通过求解式(5)来获取对应的驻定相位点

(5)

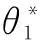
(6)

(7)

由此可知CSAR回波对应两个驻定相位点，其频谱将有两部分组成.对于线性SAR，其距离徙动曲线形如单边双曲线，且在观测角内仅有一个极值.因此线性SAR对应唯一的驻定相位点.对于圆周SAR，其距离变化曲线不再是单边双曲线，而是形如正弦函数，且在观测角θ内对应两个极值点，因而圆周SAR信号频谱对应两个驻定相位点.将由式(6)、(7)求解得到的驻定相位点代入式(4)，可以得到CSAR在(k,ξ)域的二维频谱为：

S(α,β,k,ξ)=Sa(α,β,k,ξ)+Sb(α,β,k,ξ)

(8)

式中子频谱Sa(α,β,k,ξ)和Sb(α,β,k,ξ)分别表示为

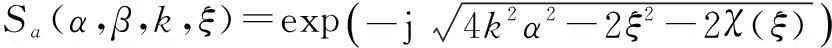
Sa(α,β,k,ξ)=exp-j4k2α2-2ξ2-2χ(ξ)()

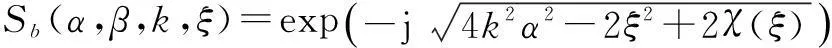
Sb(α,β,k,ξ)=exp-j4k2α2-2ξ2+2χ(ξ)()

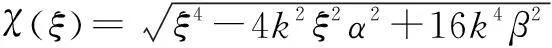
(9)

式(9)表明，对于某一目标(r,φ,0)，其全孔径回波对应的方位角度波数带宽约为4krcosθz.

本节分析了CSAR的回波频谱形式，这是CSAR频域成像处理的基础.

3信号频谱由斜距平面向地平面的投影

3.1CSAR频谱由斜距平面向地平面的投影处理

对于线性SAR，人们通常选用斜距平面进行频域信号处理，并将成像结果呈现在斜距平面上.针对CSAR，这一处理不再合适，因为CSAR对应的斜距面不再是一个平面.文献[1]论述了将CSAR频谱由斜距平面投影到成像处理平面(本文中设定为地平面)是频域成像处理的关键.具体地，文献[1]通过对CSAR系统核函数的共轭转置来近似获取CSAR地平面频谱.但这一处理的不足体现在该方法仅适用于场景中心点及其附近区域.更重要的是，人们无法对该近似处理引入的误差及成像失真做出测量和评估.针对这一问题，本文通过构造补偿函数，以匹配滤波的形式更为精确地实现了CSAR频谱由斜距平面向地平面的投影.

结合图1所示成像几何可知场景中任一目标(r,φ,0)对应的雷达入射角可以表示为：

(10)

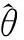
令H=0，此时斜距平面CSAR频谱S(α,β,k,ξ)等效为地平面频谱，经化简，可以表示为

Sg(R,r,k,ξ)

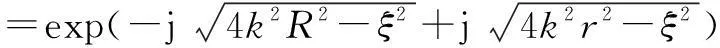
(11)

sin-1为反正弦函数.式(11)被用以构造H>0情况下对CSAR以雷达入射角θz进行投影得到的地平面频谱.

针对子频谱Sa(α,β,k,ξ)，设其对应的地平面频谱为Sa1(α,β,k,ξ)，可以将其分解为：

Sa(α,β,k,ξ)≜Sa1(R,r,k,ξ)exp(-jΩa(α,β,k,ξ))

(12)

≜表示定义为.结合式(11)，构造

Sa1(R,r,k,ξ)

(13)

Ωa(α,β,k,ξ)表示对Sa(R,r,k,ξ)投影处理需要消除的相位项.类似地，对子频谱Sb(α,β,k,ξ)进行分解，得到

Sb(α,β,k,ξ)≜Sb1(α,β,k,ξ)exp(-jΩb(α,β,k,ξ))

(14)

其中Sb1(α,β,k,ξ)表示子频谱Sb(α,β,k,ξ)对应的地平面频谱：

Sb1(α,β,k,ξ)

(15)

Ωb(α,β,k,ξ)表示对Sb(α,β,k,ξ)投影处理需消除的相位项.

观察式(12)和(14)得知，针对子频谱Sa和Sb分别以匹配滤波的方式消除相位项Ωa(α,β,k,ξ)和Ωb(α,β,k,ξ)，即可得到地平面频谱，亦实现了CSAR频谱由斜距平面到地平面的投影.在相位补偿处理中，为简化计算，有必要对Ωa(α,β,k,ξ)和Ωb(α,β,k,ξ)进行近似表达.

3.2空变相位的近似

分别对式(12)～式(15)中根号项和反三角函数利用泰勒级数进行6阶展开，得到Ωa和Ωb的近似表达式为：

Ωa(α,β,k,ξ)≈A0ξ0+A1ξ2+A2ξ4+A3ξ6

表1给出式(16)中近似表达式的系数.为评估式(16)中近似处理的可行性，我们以美国空军实验室Gotcha雷达数据参数为参考进行量化分析.设定的雷达参数如表2所示.需要指出的是，对于X波段SAR，其雷达波束较窄，加之运动过程中天线波束指向控制存在误差，实际有效的雷达观测区域较小.

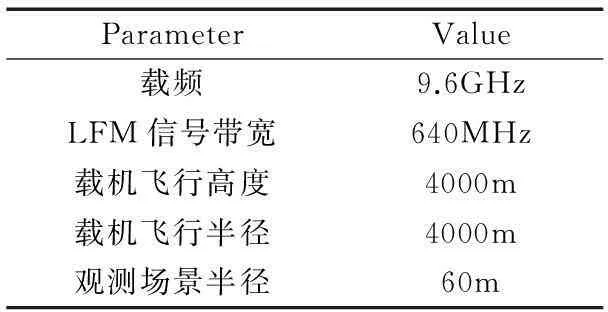
表2　雷达系统参数

观察Ωa(α,β,k,ξ)和Ωb(α,β,k,ξ)得知二者的取值同目标位置及雷达波数相关.这里将k及r均设置为其最大值，分别为207.6rad/m和60m.得到量化分析结果如图2所示.图2(a)给出了Ωa和Ωb随方位角度波数ξ的变化趋势.

图2(b)中虚线和实线分别对应Ωa和Ωb基于式(16)近似表达所引入的误差相位的变化范围，图示结果表明近似误差在数值上远小于π/4，因为近似误差对成像处理的影响可以忽略.

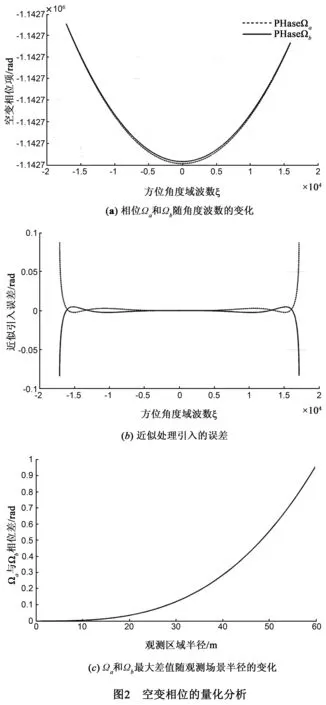
图2(c)表示不同半径处目标在其二维波数范围内对应的Ωa-Ωb最大相对变化量.观察可知Ωa和Ωb之间的差异随着目标半径的增加而增大.对于观测区域边缘处(r=60m),Ωa和Ωb项的差异大于π/4.Ωa和Ωb之间的较大差异使得我们需要分别对子频谱进行相位补偿.值得注意的是，图2中结果是基于对全孔径数据的理论分析.如本文引言中所述，现实情况下我们需要对子孔径数据进行成像处理.若Ωa-Ωb在子孔径频谱内相对变化量较小，则可以认为Ωa和Ωb近似相同，进而可以对子孔径回波频谱进行一致化相位补偿.

4CSAR子孔径成像处理

4.1角度维子孔径划分

本文成像处理的核心思想是：先对子孔径内回波数据相参积累，随后对各子孔径图像进行非相参叠加以得到最终的CSAR雷达图像.图3以边缘点目标(Ra,0,0)为例给出了子孔径数据对应的角度波数带宽示意图.设子孔径Θs对应的观测角范围为[θ-,θ+].

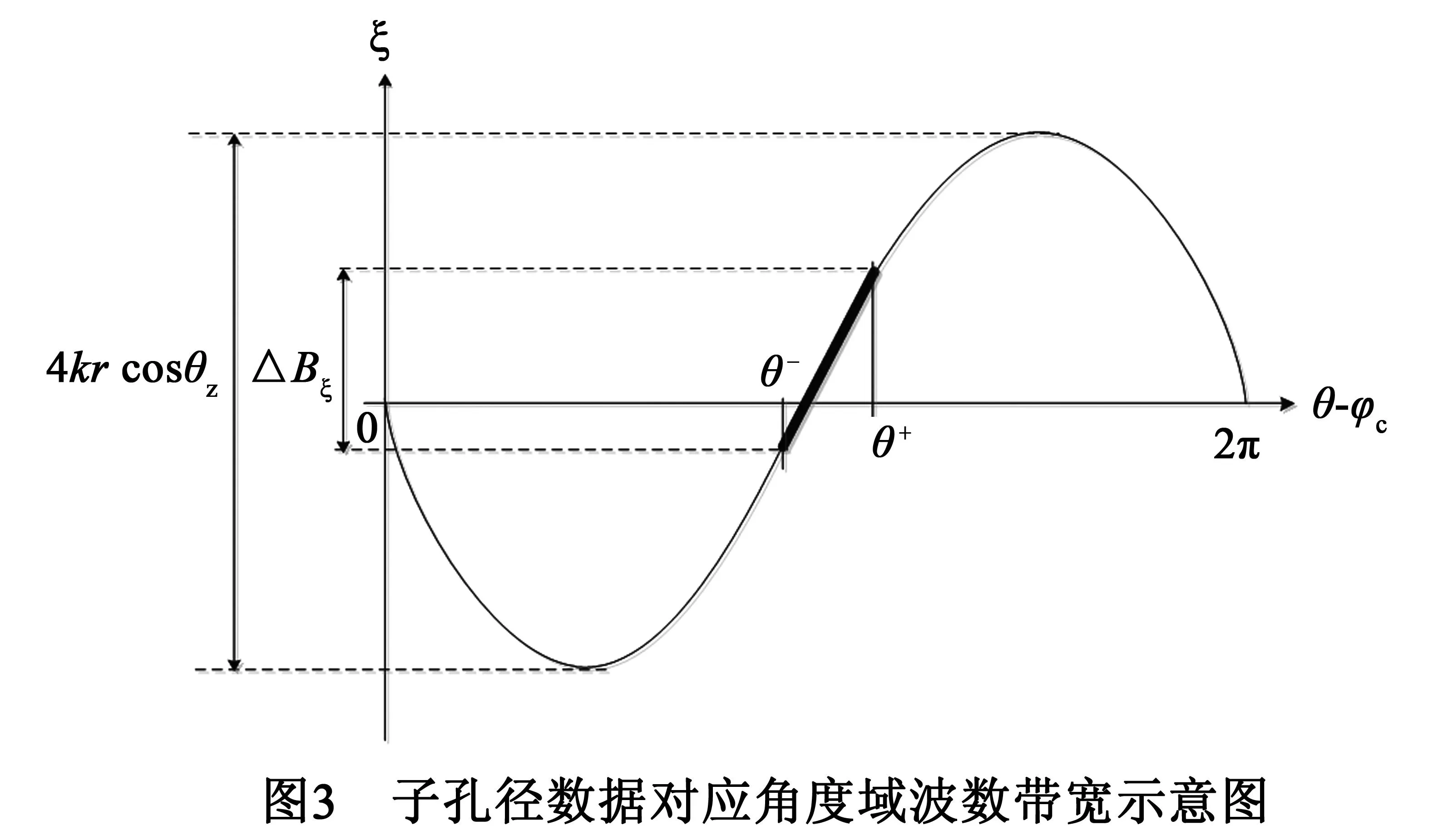
图3中曲线表示角度波数ξ随θ的变化趋势.结合式(9)，对于全孔径数据，点目标(Ra,0,0)对应的角度波数带宽约为4krcosθz.对于子孔径数据，其对应的角度波数带宽为ΔBξ且满足

φ∝ΔBξ∝(Ωa-Ωb)

(17)

式(17)表示子孔径观测角宽度的增大会引起角度域波数带宽的增大，进而使得Ωa-Ωb的差值增大.在实际处理中，应根据目标的散射特性设置子孔径带宽.文献[5]表明针对X波段CSAR,目标散射主波束宽度一般不大于20°.不失一般性，本文设子孔径观测角宽度为36°.取k=207.6rad/m,Ra=60m，经计算得到：对于观测角度为36°的子孔径数据，观测场景边缘处目标对应的Ωa-Ωb的相对最大值为0.58rad，小于π/4.这表明利用Ωa对子频谱Sb(α,β,k,ξ)进行相位补偿以消除相位项Ωb在整个观测场景范围内是成立的，亦表明了可以针对子孔径回波频谱进行一致化相位补偿，这将大大提高成像效率.

具体地，我们可以得到针对子孔径数据的补偿函数为：

Hcom=exp(j(A0ξ0+A1ξ2+A2ξ4+A3ξ6))

(18)

式(18)中第二个指数项是为了消除地平面频谱中的空不变相位.待实现了圆周SAR信号频谱由斜距平面向地平面的投影，将回波信号经角度维逆傅里叶变换至(k,θ)域.随后通过极坐标插值得到(kx,ky)域的信号频谱[1](kx,ky分别表示x向，y向对应的波数),并经二维逆傅里叶变换得到最终CSAR图像.

4.2径向子块划分

在频域成像处理中，仍需要克服式(18)中补偿函数是随目标径向距离的空变性.本文采用子带划分的方法来克服这一空变性.在子带划分的过程中，沿径向距离的宽度选择是关键步骤.在此过程中，仅以式(18)中ξ的零阶及2阶项为依据判断已足够精确.具体地，以r处匹配滤波函数对r+Δr处目标进行匹配滤波引入的相位误差为：

Pe

(19)

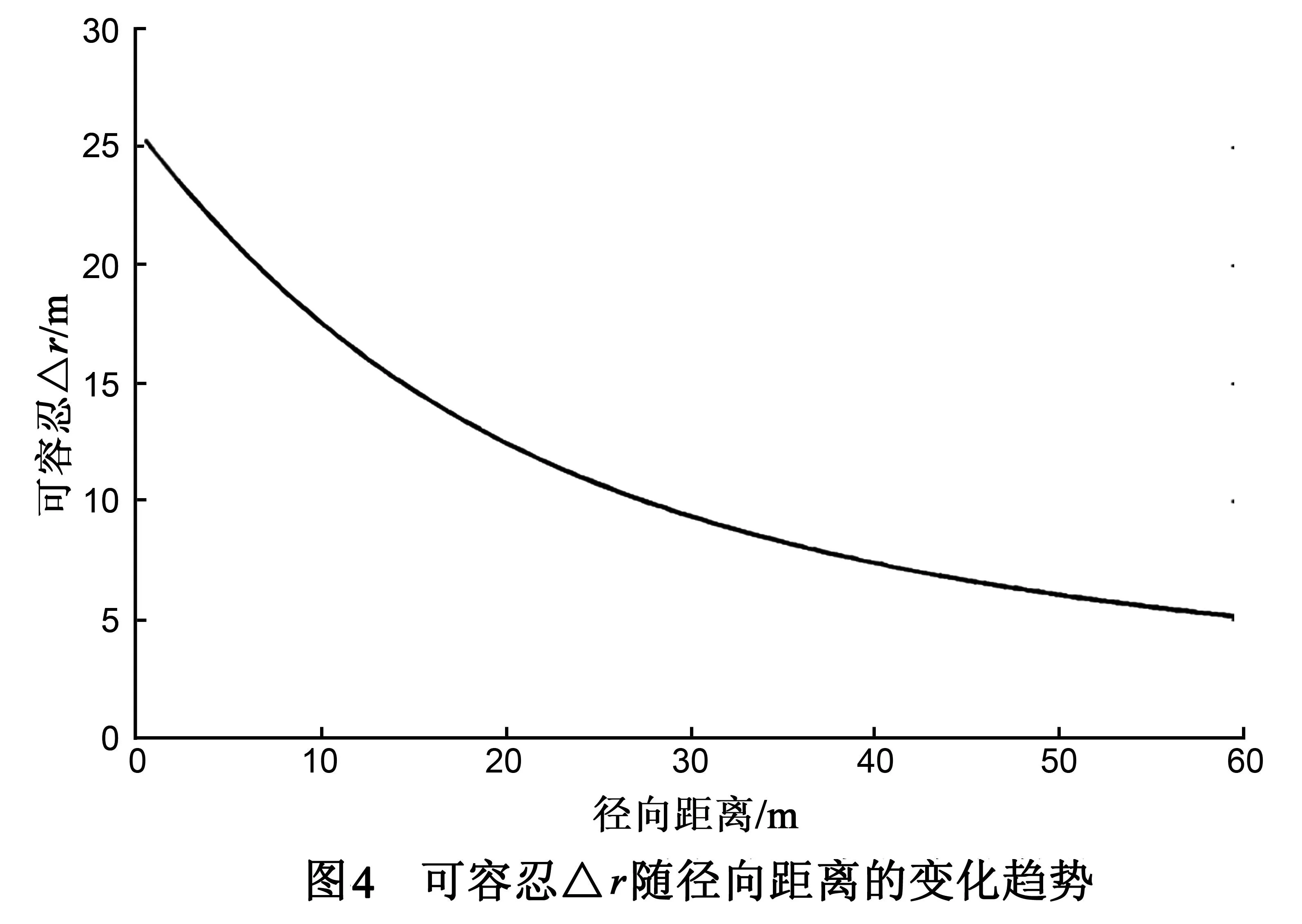
类似地，我们也可以得到以r处匹配滤波函数对r-Δr处目标进行匹配滤波引入的相位误差.这里不再赘述.式(19)尽管表达形式复杂，但却便于计算得到.我们以频谱支撑域内相位误差不能超过π/4为容限，可以得到针对不同半径处最大的可容忍Δr，如图4所示.图4给出了子带宽度随径向距离的变化趋势，这为成像区域的划分提供了依据.

基于4.1及4.2节分析，可以得到CSAR子孔径成像处理的流程如图5所示.图5中成像流程涵盖了子孔径划分以及子带划分，适用于对较大区域进行精确成像.此外，子孔径及子带处理有利于成像算法的并行化处理.

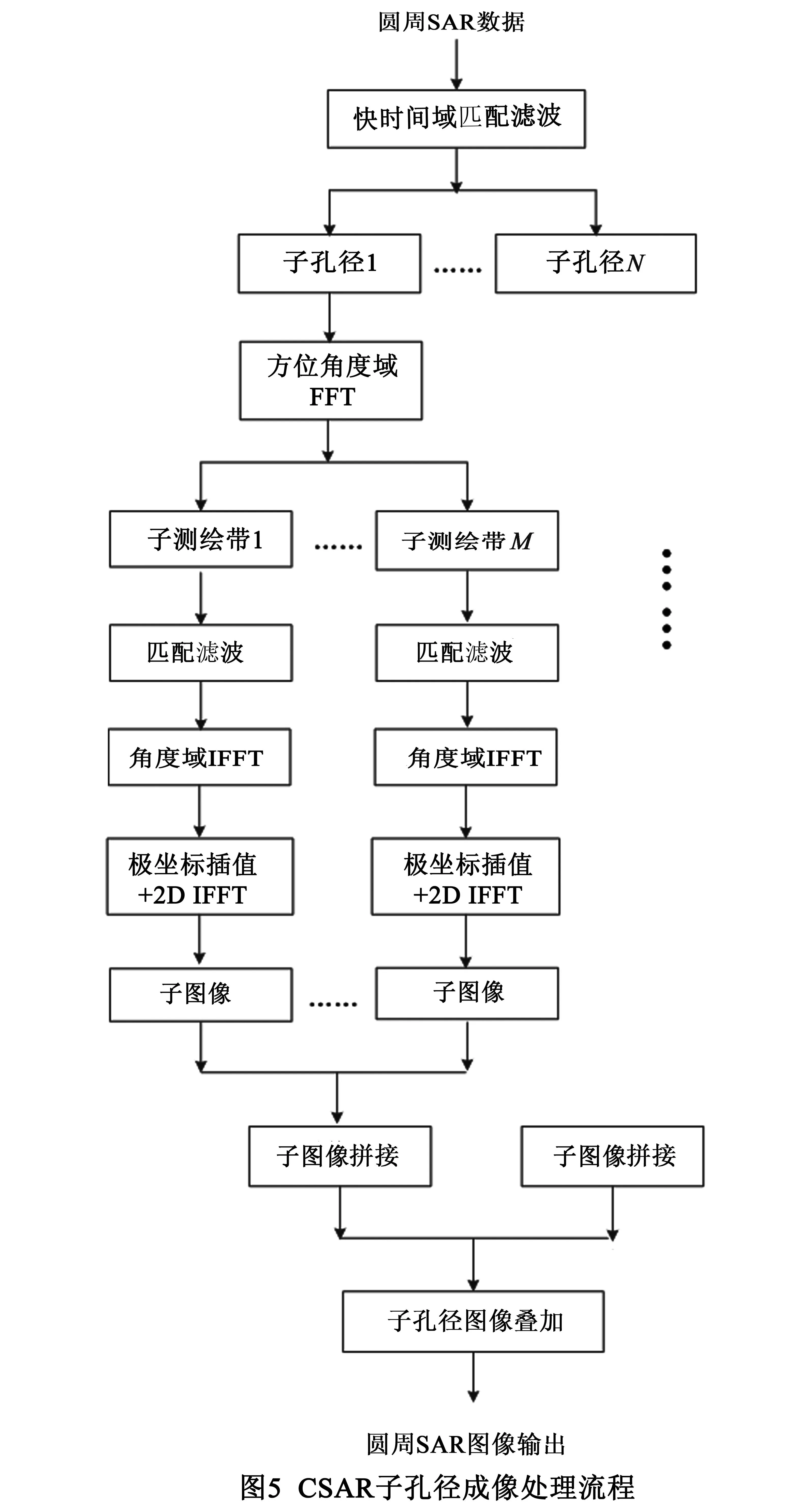
4.3运算量分析

相比于BP算法，频域成像处理的优势体现在算法实现的高效率.这里针对同一子测绘带成像结果进行量化对比.设某一子孔径数据矩阵沿方位向和距离向分别有Na，Nr个采样点；设子测绘带图像对应的像素点数为M.设回波频谱在(kx,ky)域对应的矩阵大小为N×N.结合图5，可以评估频域成像处理和BP成像处理的运算量，如表3所示.

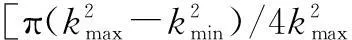
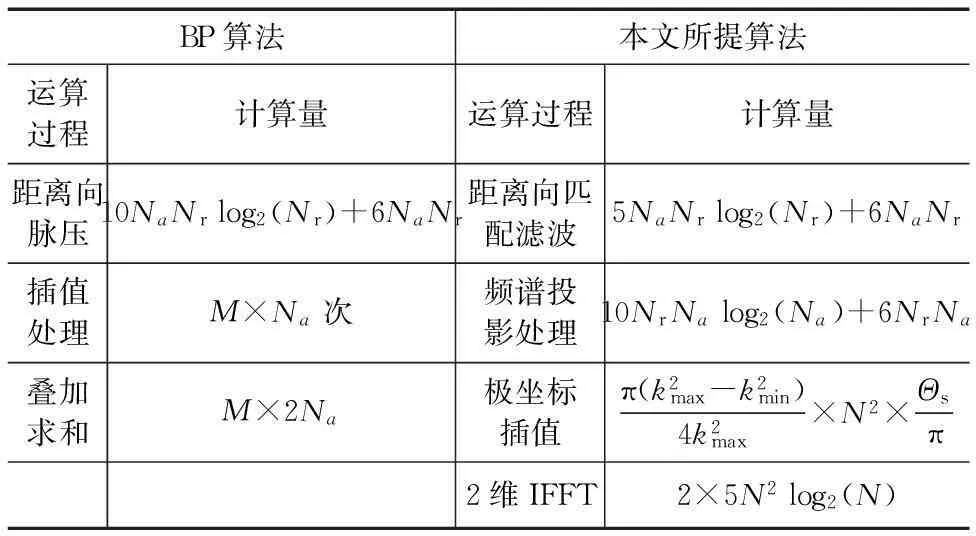
表3　运算量分析

5仿真分析

基于第4节提出的子孔径成像算法，本节利用计算机仿真分析子孔径成像处理的特性.雷达系统参数如表2所示.设子孔径观测范围为[0,36°]且点目标在此观测范围内具有恒定的电磁散射系数1.仿真试验中，设定观测场景半径为60m.并在半径60m及55m处分别均匀布置24个点目标，如图7(a)所示.结合图5中数值分析，对于r=55m处，其子带r±Δr范围可设为[50m,60m].在匹配滤波过程中，利用r=55m处匹配函数进行一致化匹配滤波处理可以得到半径范围为[50m,60m]的精确聚焦子带图像.具体的子孔径成像处理结果如图6所示.图6(a)表示点目标设置示意图，图6(b)表示子孔径数据在(kx,ky)域的频谱支撑域，它是圆环的一部分.图6(c)表示子孔径成像结果.为凸显成像结果的细节，图6(c)给出了(-60m，0m)处点目标的成像结果.

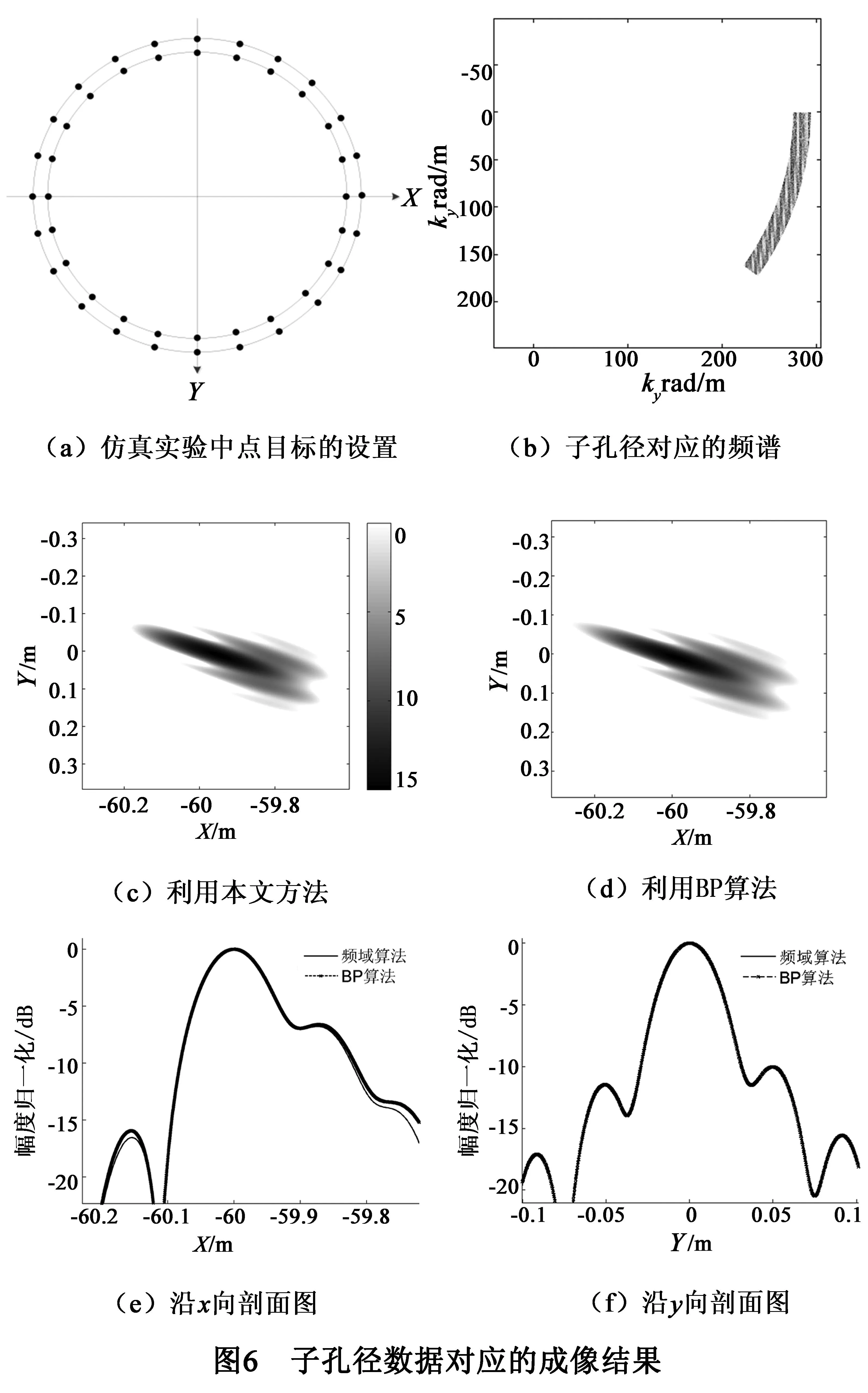
不同于线性SAR，CSAR成像对应的点散布函数难以用解析表达式精确得到[1,11].为验证成像结果，我们采用BP算法对同样的雷达仿真回波进行成像处理，得到图6(d)所示结果.图6(e)和(f)分别对应于图6(c)和(d)中点散布函数沿x，y向的剖面图.对比可知频域成像结果同BP成像结果吻合良好，表明了本文所提信号模型的正确性，亦表明了第4节子孔径及子带划分处理的可行性.由于圆周SAR子孔径成像对应的点散布函数特性不同于人们所熟知的线性SAR.图6(e)及(f)意在表明频域算法同BP算法具有相同的成像结果.圆周SAR子孔径成像对应的点散布函数特性，不在本文分析范畴之内.在上述仿真过程中，Na为3600，Nr为1024，N为11800，图像像素大小为0.01m×0.01m.基于文献[12]针对插值处理的运算量估计方法，本文采用的插值核函数长度为8，则单次插值运算对应的浮点运算数为30次.由此可以得到频域处理及BP算法对应的总的浮点运算数为2.492×1010和3.981×1012.进而可知：相比于BP算法，本文所提方法的加速比约为160.

类似于图6，我们可以得到不同的子孔径图像.若对所有子孔径图像进行非相干叠加，可以得到如图7所示结果.图7(a)和(b)分别表示(-60m,0m)处各向同性点目标对应的全孔径相参处理与子孔径图像非相参叠加对应的结果.图7(c)和(d)为图7(a)和(b)中点散布函数沿x,y向的剖面图：实线曲线和点状曲线分别代表全孔径成像和子孔径成像结果.其对应的量化参数如表4所示.

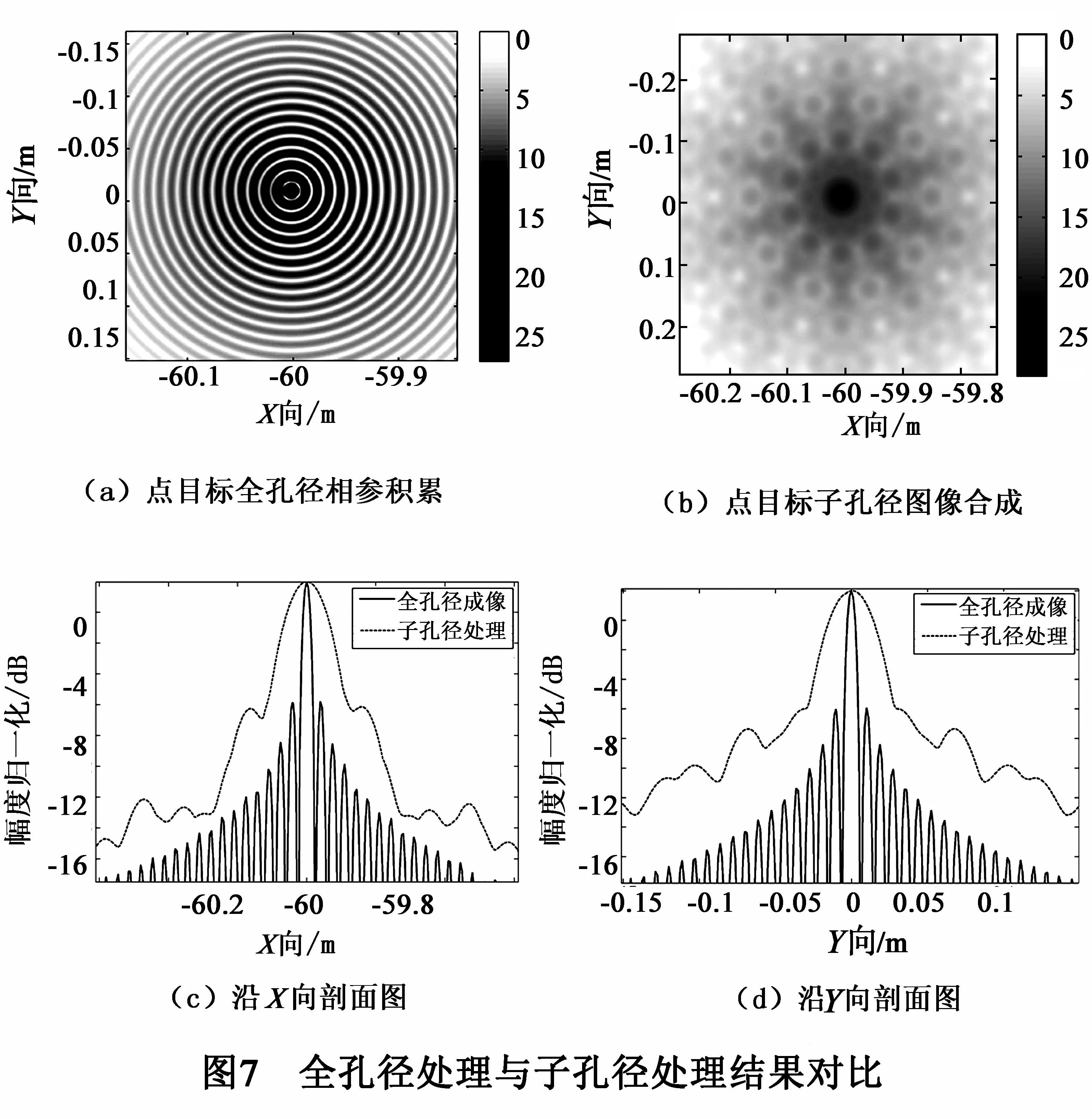
表4　点目标成像特性分析

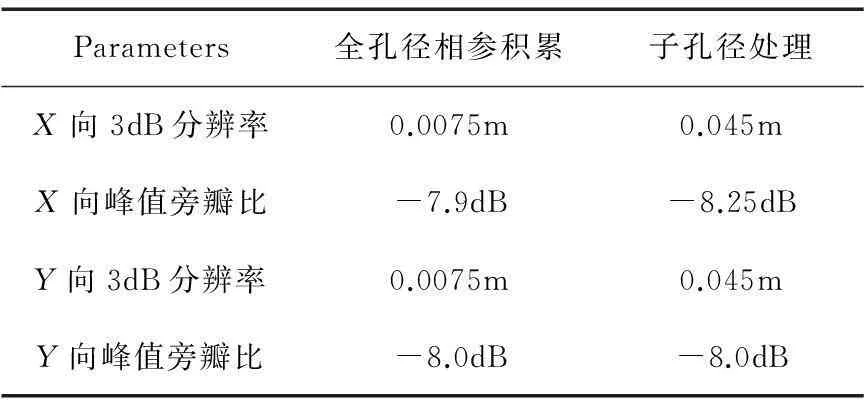
Parameters全孔径相参积累子孔径处理X向3dB分辨率0.0075m0.045mX向峰值旁瓣比-7.9dB-8.25dBY向3dB分辨率0.0075m0.045mY向峰值旁瓣比-8.0dB-8.0dB

由图7及表4可知，对于各向同性点目标，子孔径成像处理对应的3dB分辨率由0.0075m降低至0.045m；第一旁瓣电平未有明显降低.子孔径处理虽然不能得到亚波长级的空间分辨率，但其处理流程更符合实际情况，具有更高的效率和更为广泛的实用性.现实情况下，需要对各子测绘带图像进行拼接，如何减小拼接过程中的图形失真将是后续工作的重点.

6结论

本文给出了CSAR精确的二维频谱表达形式；结合现实场景中大多数目标散射特性的方位空变性，以匹配滤波的形式完成了CSAR频谱由斜距平面向地平面的投影；通过径向子带划分克服了匹配滤波处理沿径向距离的空变性.提出了一种完整的子孔径成像流程.文中结合典型X波段CSAR参数开展仿真试验，试验结果证实了文中所提信号模型以及成像处理流程的正确性,表明了频域成像处理的高效性.

参考文献

[1]Soumekh,M Synthetic Aperture Radar Signal Processing with Matlab Algorithms[M].New York:John Wiley & Sons Inc,1999.

[2]Yun Lin,Wen Hong,Weixian Tan,Yirong Wu.Extension of range migration algorithm to squint circular SAR imaging[J].IEEE Geoscience and Remote Sensing Letters,2011,8(4):651-655.

[3]闵锐.机载SAR三维成像理论及关键技术研究[D].成都：电子科技大学,2008.

Min Rui.Research on Airborne SAR Three-Dimensional Imaging Theory and Key Technology[D].Chengdu：University of Electronic Science and Technology of China，2008.(in Chinese)

[4]刘燕.高分辨率及新模式SAR成像算法研究[D].西安：西安电子科技大学,2012.

Liu Yan.Study on High-Resolution SAR and New Type SAR Imaging[D].Xi′an:Xidian University,2012.(in Chinese)

[5]H Cantalloube,E Colin.Assessment of physical limitations of high resolution on targets at X-band from circular SAR experiments[A].EUSAR Conference[C].Friedrichshafen,Germay:IEEE,2008.1-4.

[6]Ponce,O,Prats-Iraola P,et al.Fully polarimetric high-resolution 3-D imaging with circular SAR at L-band[J].IEEE Transactions on Geoscience and Remote Sensing,2013,52(6):3074-3090.

[7]洪文.圆迹SAR成像技术研究进展[J].雷达学报，2012，1(2):124-135.

Hong Wen.Progress in circular SAR imaging technique[J].Journal of radars,2012,1(2):124-135.(in Chinese)

[8]保铮，邢孟道，王彤.雷达成像技术[M].北京：电子工业出版社.2005.

[9]贾高伟,常文革.FMCW SAR运动补偿处理技术研究[J].电子学报,2013,41(9):1665-1671.

Jia Gaowei,Chang Wenge.Analysis of motion compensation for FMCW SAR[J].Acta Electronica Sinica,2013,41(9):1665-1671.(in Chinese)

[10]林赟，谭维贤，洪文，王彦平，吴一戎.圆迹SAR极坐标格式算法研究[J].电子与信息学报，2010,32(12),2802-2807.

Lin Yun,Tan Weixian,Hong Wen,et al.Polar format algorithm for circular synthetic aperture radar[J].Journal of Electronics &Information Technology,2010,32(12):2802-2807.(in Chinese)

[11]Prats-Iraola,P,Rodriguez-Cassola,M,et al.Efficient evaluation of Fourier-based SAR focusing kernels[J].IEEE Geoscience and Remote Sensing Letters,2014,11(9):1489-1493.

[12]Cumming I G,Wong F H.Digital Processing of Synthetic Aperture Radar Data:Algorithms and Implementation[M].Norwood:Artech House,2005.

贾高伟男，1989年出生，河南周口人，博士研究生，研究方向为高分辨SAR成像，运动补偿算法与实现.

E-mail:jiagaoweinudt@gmail.com

常文革男，1965年出生，陕西岐山人，教授，博士生导师，研究方向包括超宽带雷达成像与处理，实时信号处理，被动干涉SAR.

Fourier-Based Sub-aperture Imaging Algorithm for Circular Synthetic Aperture Radar

JIA Gao-wei,CHANG Wen-ge

(CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology，Changsha，Hunan410073，China)

Abstract:With the characteristics like super-high resolution,three-dimensional imaging,and all-aspect angle observation,circular synthetic aperture radar (CSAR) has become the hotspot in the field of SAR.In practice,almost all the observed targets are anisotropic targets thus it is not necessary to carry out the coherent processing within the whole aperture.Correspondingly,a Fourier-based sub-aperture imaging flow which has higher efficiency is proposed.The expression and analysis of the spectrum of CSAR are presented,as well as the proposed Fourier-based imaging flow.Theoretical analysis and simulation test depict that both the proposed signal model and the imaging flow are available for CSAR.

Key words:circular synthetic aperture radar;Fourier-based imaging;sub-aperture imaging

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.001

中图分类号:TN957

文献标识码：A

文章编号：0372-2112 (2016)03-0497-08

收稿日期:2014-08-28；修回日期：2015-02-03;责任编辑：梅志强