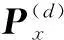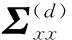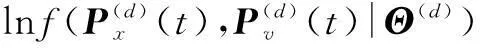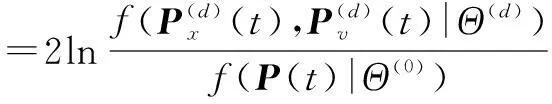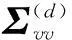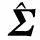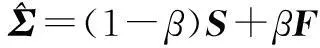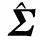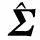一种新的基于EEF准则的空间声源个数估计算法

黄青华,张翼飞,刘　凯

(上海大学通信与信息工程学院,上海 200072)



一种新的基于EEF准则的空间声源个数估计算法

黄青华,张翼飞,刘凯

(上海大学通信与信息工程学院,上海 200072)

摘要：针对指数嵌入族(Exponentially Embedded Families,EEF)准则在快拍数小于阵元数情况下无法估计声源个数的问题,本文提出一种新的空间声源个数估计算法.首先通过球麦克风阵列采集空间声场高阶信息,建立球阵列信号模型,将声源个数估计扩展到三维空间.继而将观测信号空间分解为信号子空间和噪声子空间,利用最小均方差(Minimum Mean-Squared Error,MMSE)方法估计观测信号空间及噪声子空间的协方差矩阵,确保矩阵估计的一致性和准确性.在此基础上改进似然比函数,同时引入新的自由度计算,使得算法在快拍数小于阵元数的情况下能有效估计声源个数.仿真结果表明,在进行空间声源个数估计时,相对于EEF准则,新的算法不仅适用于快拍数小于阵元数情况,同时提高了估计准确率.

关键词:空间声源个数估计;球麦克风阵列;指数嵌入族准则;最小均方差

1引言

信源个数估计是阵列信号处理的首要环节,在雷达、声纳、勘探、通信和生物医学等多个领域都有广泛的应用.大多数信源个数估计算法都是以线阵和平面阵[1,2]为基础建立信号模型进行个数估计.近年来,球阵逐步受到人们的重视,由于具有三维空间的旋转对称结构和较高的空间分辨率,球阵相对于线阵和平面阵,能够对空间源场进行更加充分的采样[3].

准确的信源个数估计是各类空间谱估计算法的前提条件,决定着信源定位和分离等处理的性能优劣.Wax和Kailath[4]首次将信息论准则引入信源个数估计中,提出Akaike信息准则(Akaike Information Criterion,AIC)和最小描述长度(Minimum Description Length,MDL)准则,解决了假设检验类方法需要人为设定阈值的问题.但AIC在小样本的情况下存在过估计的问题,而且AIC不属于一致性估计.MDL准则是一致性估计,但在小样本和低信噪比的情况下存在欠估计问题[5].此后,许多学者提出了一些基于信息论准则的改进算法.Wax[6]采用正交投影的方法对观测数据进行空间分解,将MDL准则应用到了多相干信源个数的估计中.Huang和Wu[7]提出了一种低复杂度的MDL方法,利用多级维纳滤波器对观测数据进行快速空间分解,降低了计算复杂度,并且适用于低快拍数和低信噪比的情况.Xu和Kay[8]将指数嵌入族理论应用到信源个数估计问题中,采用均匀线性阵列估计平面内的信源个数.相对于MDL准则,EEF引入似然比函数,在低快拍数和低信噪比情况下具有更高的估计准确率.但现有EEF准则采用的样本协方差矩阵,作为协方差矩阵的估计,在快拍数小于阵元数的情况下无法有效估计协方差矩阵[9],直接影响到EEF准则的估计性能.

随着3D音频的发展,三维空间多声源个数估计受到了广泛关注.本文利用球麦克风阵列采集空间声场信息,建立球阵列信号模型,进行三维空间上的声源个数估计.考虑到EEF准则的优缺点,提出一种新的基于EEF准则的空间声源个数估计算法.首先将观测信号空间分解为信号子空间和噪声子空间,通过求取空间分解后的最大似然函数,产生新的似然比函数.然后利用最小均方差方法得到观测信号空间及噪声子空间协方差矩阵的一致性估计矩阵,改进自由度计算,提高声源个数估计性能.新的算法在低信噪比和低快拍数以及小角度间隔情况下提高了个数估计准确率.

2空间声源个数估计

2.1球阵列信号模型

L个相互独立、各向同性的麦克风分布在半径为R的刚性球体表面.建立球坐标系如图1所示.球麦克风阵列的球心为坐标系原点O,阵元l(l=1,2,…,L)的位置可表示为Rl=(R,Ωl),其中Ωl=(θl,φl),θl和φl分别表示阵元l的俯仰角和方位角.

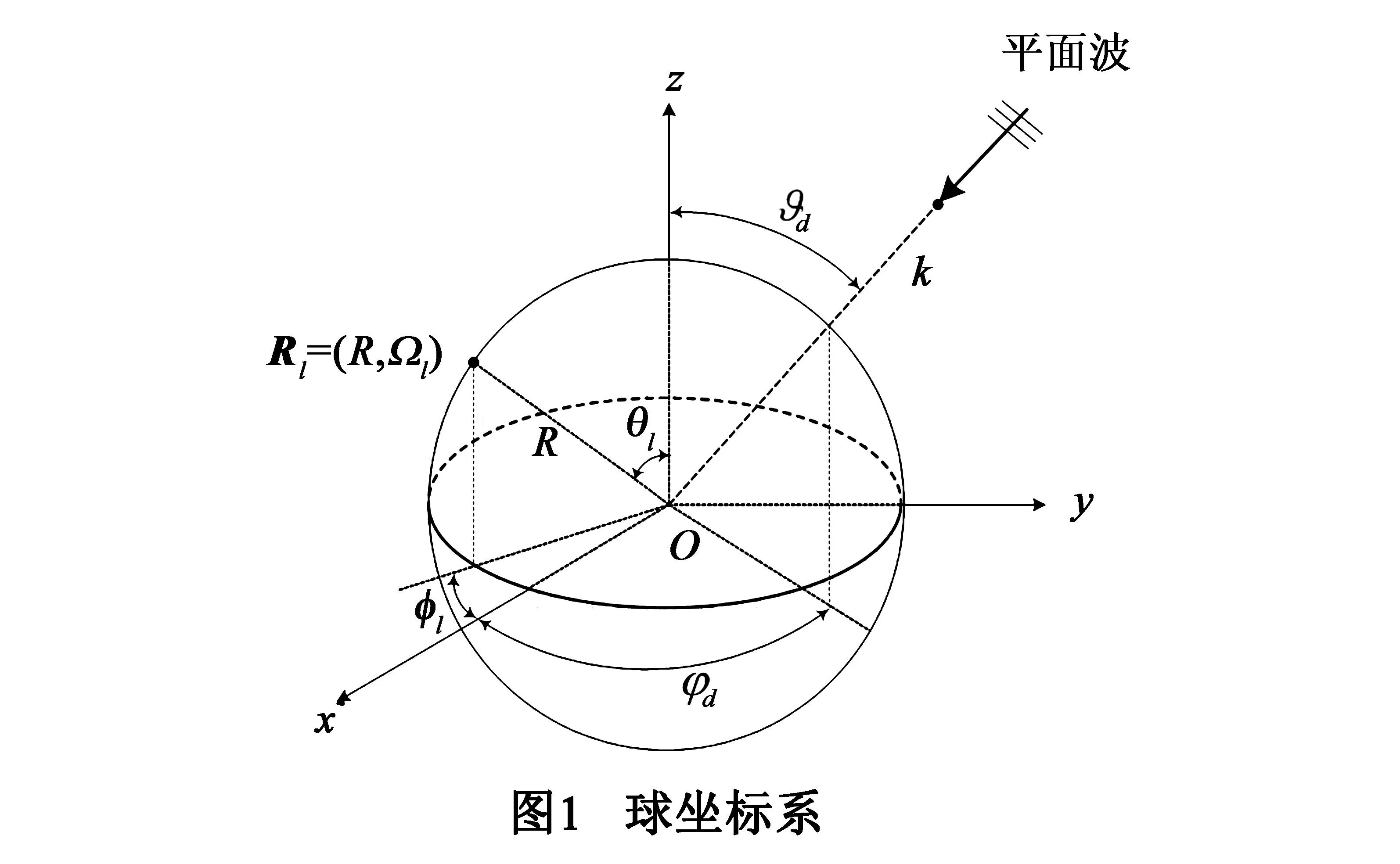
远场条件下,从Φd=(ϑd,φd)方向入射一单位幅度的窄带平面波,波数k=ω/c,ω为平面波的角频率,c为声速.平面波在阵元l处产生的声压可表示为[10]:

(1)

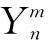
(2)

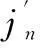
现假设有D个窄带平面波,分别从不同位置入射到球麦克风阵列,受高斯白噪声的影响,阵元l处的实际声压为[11]:

(3)

t=1,2,…,T表示快拍数,xd(k,t)是Φd方向入射平面波幅度,d=1,2,…,D.v(k,Ωl,t)表示阵元l上的噪声幅度.

球麦克风阵列接收的信号向量可以写作:

P(t)=AX(t)+V(t)

(4)

其中,P(t)=[p(k,Ω1,t),p(k,Ω2,t),…,p(k,ΩL,t)]T表示观测信号,X(t)=[x1(k,t),x2(k,t),…,xD(k,t)]T表示入射声源信号,V(t)=[v(k,Ω1,t),v(k,Ω2,t),…,v(k,ΩL,t)]T表示噪声,(·)T为矩阵的转置,用σ2表示噪声功率,噪声与声源信号之间相互独立,A是一个L×D的导向矩阵,它描述声源信号到阵元的空间传输特性.根据式(1),导向矩阵A可分解为:

A=Y(Ω)BYH(Φ)

(5)

Y(Ω)是一个L×(N+1)2的球谐矩阵:

(6)

B是一个(N+1)2×(N+1)2的对角矩阵:

(7)

Y(Φ)是一个D×(N+1)2的球谐矩阵,与Y(Ω)结构相同,(·)H表示共轭转置.

P(t)的协方差矩阵为Σ=Ε{P(t)PH(t)},Ε{·}代表数学期望.用λl(l=1,2,…,L)表示Σ的特征值.其中λl满足如下规律:

λ1≥…≥λD≥λD+1=…=λL=σ2

(8)

根据上述规律,只要找出(L-D)个重复的较小特征值,就可以确定声源个数D.考虑到实际情况下,Σ无法精确得到,一般由样本协方差矩阵S估计.S可通过观测信号的有限个快拍数据求取:

(9)

用cl(l=1,2,…,L)表示样本特征值,其排列规律如下:

c1≥…≥cD≥cD+1≥…≥cL

(10)

可以看出,样本协方差矩阵的特征值呈现出一种非递增规律,利用较小特征值来确定声源个数D会引起较大估计误差.在以均匀线阵为模型的信源个数估计问题中,EEF准则在保证了一致性的同时,估计性能在低信噪比、低快拍数情况下相对于MDL准则有所提升.

2.2基于EEF准则的估计算法

假设声源个数为d,协方差矩阵Σ可表示为:

(11)

IL表示L×L单位矩阵,用Θ(d)表示信号模型的参数向量:

(12)

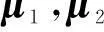
(13)

EEF准则可表示为:

(14)

wd=d(2L-d)+1

(15)

u(·)表示阶跃函数,wd表示参数Θ(d)的自由度.EEF(d)取最大值时所对应d值即为待估计的声源信号个数.

EEF准则通常采用样本协方差矩阵S作为Σ的估计矩阵.在L≤T的情况下,S属于无偏估计,但其均方差过高;在L>T的情况下S的估计偏差过大[9].其次,基于信息论的声源个数估计准则大都是在T>L的情况下进行运算的[4～6],此时Σ的特征值个数为L,但在T

针对上述问题,本文提出了一种新的基于EEF准则的估计算法.首先引入空间分解概念,将观测空间分为信号子空间和噪声子空间,求解空间分解后的似然函数,使得似然比函数中包含观测空间和噪声子空间的协方差矩阵.进而利用MMSE方法估计两协方差矩阵,得到更准确的一致性估计矩阵.改进自由度的计算,最终得到该估计算法.

3新的空间声源个数估计算法

已知观测向量P(t)的协方差矩阵Σ的维数为L×L.当快拍数T≥L时,Σ为满秩矩阵,非零特征值个数为L;T

(16)

(17)

信号和噪声子空间与观测空间存在如下关系[13]:

(18)

将式(18)代入到式(16)中得:

(19)

相应的对数似然比函数可表示为:

(20)

(21)

(22)

现有多种基于MMSE的矩阵估计算法,如OAS、RBLW等,不同方法构造出的收缩系数ρ不同,这些算法大都是通过矩阵运算求得ρ[9].为得到更加准确的估计矩阵,本文利用样本特征值[13]求解ρ如下:

(23)

cl(l=1,2,…,ε)为样本特征值,考虑到实际计算时ρ可能大于1,用β=min(ρ,1)[9]代替ρ带入式(22)中,得到估计矩阵如下:

(24)

(25)

(26)

(27)

(28)

对观测空间进行空间分解后,信号子空间自由度为d2,噪声子空间自由度为1,得到总的自由度为d2+1.文献[14]指出,计算自由度时,应着重考虑信号子空间的d个特征向量,信号子空间的d个特征值可忽略,得到新的自由度:

(29)

接下来的仿真结果表明,改进的自由度计算可使估计性能得到进一步改善.

最终,将式(28)和式(29)代入EEF准则,得到新的基于EEF准则的空间源个数估计算法NEEF(Novel Exponentially Embedded Families)算法.可得:

(30)

NEEF(d)取最大值时所对应d的值即为声源信号的个数.当d=D时,声源个数估计正确.新的算法不仅适用于球阵列,在基于线阵及平面阵的声源个数估计问题中同样适用.

4仿真实验

采用一个半径R=5cm,阵元数为32元的均匀球麦克风阵列.通过MATLAB进行5组仿真实验,每组仿真结果都是经过2000次Monte Carlo实验得到的.以准确估计的概率作为评价指标,验证改进自由度公式对新算法估计性能的改善以及新算法在空间声源个数估计问题中的有效性.

第1组实验中三个平面波分别从(112°,76°),(208°,119°)和(238°,95°)方向入射,信噪比从-10dB以步长1dB变化到0dB.自由度公式对新算法估计性能的影响如图2所示.NEEF(40)、NEEF(20)分别表示在快拍数为40和20时,NEEF算法的估计概率曲线.ODOF-EEF (40)、ODOF-EEF(20)分别表示在快拍数为40和20时,NEEF算法在不改变自由度公式情况下得到的估计概率曲线,ODOF-EEF (Original Degrees Of Freedom Exponentially Embedded Families)算法表示将原始自由度公式(15)以及改进过后的似然比函数式(28)带入EEF准则得到的算法.可以看出,在T=40和T=20情况下,NEEF的估计准确率均高于ODOF-EEF的准确率.且T=20情况下NEEF的准确率高于T=40时ODOF-EEF的准确率.

第2组实验采用和第1组相同的声源,信噪比同样从-10dB以步长1dB变化到0dB.声源个数正确估计的概率和信噪比之间的关系如图3所示.NEEF(40)、NEEF(20)分别表示在快拍数为40和20时,NEEF的估计概率曲线,EEF(40)、EEF(20)分别表示在快拍数为40和20时,EEF的估计概率曲线.可以看出在快拍数T=40的情况下,NEEF和EEF方法都可以准确估计声源个数,但是在低信噪比情况下,NEEF优于EEF方法.在T=20情况下,EEF准则无法估计声源个数,然而NEEF仍具备较高的估计准确性,可以看出此时NEEF的估计准确率和EEF准则在T=40情况下的估计准确率相近.

第3组实验中采用和第1组相同的声源,信噪比为-4dB,快拍数从10以步长10变化到70.仿真结果如图4所示,随着快拍数的增加,两者准确估计声源个数的概率也随之增大.当快拍数低于阵元数时,EEF准则无法准确估计声源的个数.快拍数为10时,NEEF准则估计的准确率逐渐升高,当快拍数增大到30时,NEEF的估计准确率达到1,可以准确估计声源个数.

第4组实验中信噪比取10dB.两个平面波分别从(112°,76°)和(208°,119°)方向入射,第三个平面波与第一个平面波的方位角之差从1°变化到10°,俯仰角和第一个平面波相同.基于NEEF和EEF准则的空间声源个数正确估计概率如图5所示.可以看出,T=40时,NEEF和EEF方法都可以准确估计声源个数,但NEEF准则的估计准确性要高于EEF方法.T=20时,传统EEF方法无法正确估计声源个数,而NEEF的估计性能从方位角为2°开始逐步提高,且方位角在3°到6°范围内时,NEEF的估计准确率高于快拍数为40情况下EEF的估计准确率.

第5组实验信噪比取8dB,声源个数从1以步长为1变化到10.第i(i=1,2,…,10)个声源的方位角和俯仰角均为(20i)°,从图6可以看出在T=40情况,EEF和NEEF方法都可以准确估计声源个数.在T=20情况下,EEF方法无法正确估计声源个数,当声源数小于5时,NEEF仍具有正确估计声源个数的能力,随着声源数增大,估计准确率急剧下降.

5总结

本文通过球麦克风阵列采集空间声场信息,利用球谐函数分解声场,建立球阵列信号模型,从而进行空间声源个数估计.针对EEF准则在快拍数小于阵元数情况下无法有效估计声源个数的问题,提出了一种新的基于EEF准则的空间声源个数估计算法.算法通过引入空间分解将观测空间划分为信号子空间和噪声子空间,改进似然比函数及自由度计算,利用MMSE估计观测空间和噪声子空间的协方差矩阵,提高了矩阵估计的准确性,得到新的声源个数估计算法.该算法相比于传统EEF在低信噪比、低快拍数以及小角度间隔等方面的估计性能得到了改善,并且在快拍数小于阵元数情况下具备估计声源个数的能力.文中所用的声源信号为非相干信号,在实际的应用中,还必须要考虑声源信号相干的情况,因此,三维空间内相干声源的个数估计问题将是下一步的研究重点.

参考文献

[1]刘鲁涛,司锡才,王立国.基于因子分析的信源数与噪声估计[J].电子学报,2011,39(4):837-841.

LIU Lu-tao,SI Xi-cai,WANG Li-guo.Source number and noise estimation based on factor analysis[J].Acta Electronica Sinica,2011,39(4):837-841.(in Chinese)

[2]Muma M,Cheng Y,Roemer F,et al.Robust source number enumeration forr-dimensional arrays in case of brief sensor failures[A].IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP) [C].Kyoto:IEEE,2012.3709-3712.

[3]Hafizovic I,Nilsen C C,Holm S.Transformation between uniform linear and spherical microphone arrays with symmetric responses[J].IEEE Transactions on Audio,Speech,and Language Processing,2012,20(4):1189-1195.

[4]Wax M,Kailath T.Detection of signals by information theoretic criteria[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1985,33(2):387-392.

[5]叶中付,向利,徐旭.基于信息论准则的信源个数估计算法改进[J].电波科学学报,2007,22(4):593-598.

YE Zhong-fu,XIANG Li,XU Xu.Improvement of source number estimation based on information theoretic criteriac[J].Chinese Journal of Radio Science,2007,22(4):593-598.(in Chinese)

[6]Wax M.Detection of the number of coherent signals by the MDL principle[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1989,37(8):1190-1196.

[7]Huang L,Wu S.Low-complexity MDL method for accurate source enumeration[J].IEEE Signal Processing Letters,2007,14(9):581-584.

[8]Xu C,Kay S.Source enumeration via the EEF criterion[J].IEEE Signal Processing Letters,2008,15:569-572.

[9]Chen Y,Wiesel A,Eldar Y C,et al.Shrinkage algorithms for MMSE covariance estimation[J].IEEE Transactions on Signal Processing,2010,58(10):5016-5029.

[10]Rafaely B.Analysis and design of spherical microphone arrays[J].IEEE Transactions on Speech and Audio Processing,2005,13(1):135-143.

[11]Huang Q,Song T.DOA estimation of mixed near-field and far-field sources using spherical array[A].IEEE 11th International Conference on Signal Processing (ICSP)[C].Beijing:IEEE,2012.382-385.

[12]Wax M.Detection and localization of multiple sources via the stochastic signals model[J].IEEE Transactions on Signal Processing,1991,39(11):2450-2456.

[13]Huang L,So H C.Source enumeration via MDL criterion based on linear shrinkage estimation of noise subspace covariance matrix[J].IEEE Transactions on Signal Processing,2013,61(19):4806-4821.

[14]Williams D B.Counting the degrees of freedom when using AIC and MDL to detect signals[J].IEEE Transactions on Signal Processing,1994,42(11):3282-3284.

黄青华女,1978年生,山东人,获得上海交通大学图像处理与模式识别研究所博士学位.现为上海大学通信与信息工程学院副教授.研究领域包括信号处理,3D音频,贝叶斯算法.

E-mail:qinghua@shu.edu.cn

张翼飞女,1991年生,河南人,获得河南大学工科学士学位.现为上海大学通信与信息工程学院硕士研究生.研究方向为阵列信号处理.

刘凯男,1981年生,湖北人,获得中国科学技术大学博士学位.现为上海大学通信与信息工程学院副教授.研究领域包括无线定位,雷达信号处理.

A Novel Spatial Acoustic Source Enumeration Algorithm Based on EEF Criterion

HUANG Qing-hua,ZHANG Yi-fei,LIU Kai

(SchoolofCommunicationandInformationEngineering,ShanghaiUniversity,Shanghai200072,China)

Abstract:The exponentially embedded families (EEF) criterion fails to enumerate sources when the number of snapshots is smaller than that of array sensors.To solve this problem,a novel estimation algorithm is proposed based on the EEF criterion in this paper.First a spherical microphone array is used to sample high-order sound field information in 3D space and the array signal model is constructed to estimate the number of spatial acoustic sources.Then the observation space is divided into a signal subspace and a noise subspace.The covariance matrices of the observation space and the noise subspace are estimated by minimum mean-squared error (MMSE) method.Based on the consistent and more accurate estimates,we calculate a new likelihood ratio function and a parameter freedom to modify the conventional EEF criterion.The proposed method can enumerate sources effectively in the case of the deficient number of snapshots.Compared with the conventional EEF criterion,simulation results demonstrate that the proposed algorithm has better performance for source enumeration.

Key words:spatial acoustic source enumeration;spherical microphone array;exponentially embedded families criterion;minimum mean-squared error

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.029

中图分类号:TN912.3

文献标识码：A

文章编号：0372-2112 (2016)03-0687-06

项目基金:国家自然科学基金(No.61001160);上海市教委创新基金(No.12YZ023);上海市自然科学基金(No.14ZR141500)

收稿日期:2014-04-29;修回日期:2014-09-05;责任编辑:梅志强