带丢包Markov切换线性系统的状态估计问题研究

周卫东,刘萌萌

(哈尔滨工程大学自动化学院,黑龙江哈尔滨 150001)



带丢包Markov切换线性系统的状态估计问题研究

周卫东,刘萌萌

(哈尔滨工程大学自动化学院,黑龙江哈尔滨 150001)

摘要：针对一类带丢包的Markov切换系统,提出一种含有双Markov切换参数的交互式多模型算法.该算法利用一个二态的Markov链对系统是否丢包进行建模,得到双Markov链系统,通过定义乘积集将两个Markov切换参数所对应的模型集进行融合,并给出单个模型集中各模型与乘积集中各模型的对应关系.在此基础上,以交互式多模型算法为框架,采用分层的方法,并利用一种新的最优估计算法对双Markov链系统进行滤波.仿真实验证明了该算法的有效性.

关键词:Markov系统;量测丢包;双Markov链;最优滤波估计;交互式多模型算法

1引言

Markov切换系统是一类包含多模态的随机混合系统.该类系统由两部分构成:系统状态和模型状态.其中,系统状态可由微分方程或差分方程表示,模型状态可用连续时间离散状态的Markov链描述,模型状态之间可通过一定的转移概率进行相互切换[1].由于Markov切换系统能够有效描述大量的结构和参数随时间变化的现实系统,因此在许多领域得到了广泛的应用,如经济领域的预测与决策、飞行器控制、目标跟踪等.而其广泛的应用背景使它成为目前国内外学者研究的热点之一,在其可控性、可观测性[2,3]、稳定性[4～6],以及滤波器设计[7～9]等方面都有着深入的研究.

在实际的传感器网络中,由于有限带宽和网络传输的不稳定性,使得数据丢包成为不可避免的问题[10].关于网络丢包问题目前已有大量的研究成果,针对单一系统的丢包问题中,文献[11]对带丢包的离散滤波器进行了研究,给出了丢包率的上界;在此基础上,文献[12]对带丢包最优滤波估计误差协方差有界的概率问题进行了研究.文献[13～16]针对含有随机时延、多次丢包以及不确定观测的线性离散随机系统的滤波问题进行了研究,分别提出了分散融合滤波器、集中式融合估计器、最优线性估计器以及次优融合估计算法.文献[17]针对网络系统的多次丢包问题利用Riccati方程提出一种在线自适应的Kalman滤波方法.文献[18]针对多次丢包情况下的离散时变系统的鲁棒问题,提出了相应鲁棒滤波器策略.文献[19]针对一类含有多次随机时变时延以及多次量测丢包的离散不确定非线性网络系统进行了研究,基于线性矩阵不等式提出一种线性全阶鲁棒滤波器.针对Markov切换系统的丢包问题中,文献[20]基于Lyapunov-Krasovskii函数和离散化不等式提出了一种指数H∞滤波器.文献[21]利用Bernoulli随机分布对系统丢包进行建模,基于随机系统SSG理论和Lyapunov函数提出一种H∞滤波器设计框架.文献[22]基于双Markov链和H∞技术提出一种鲁棒状态估计算法.文献[23]针对多目标跟踪的量测丢失问题建立了一种精确贝叶斯量测更新方程,并在此基础上提出了JIMMCPDAR算法.文献[24]将有损传感器网络建模为非线性Markov跳变时延系统,提出了一种分布式滤波器设计框架.纵观上述研究工作,针对确定的线性或非线性系统的丢包问题的研究已经比较成熟,而针对Markov切换系统中的数据丢包问题的研究仍需要进一步的发展和完善.而且这两类系统存在着本质的区别,针对确定系统所得的成果并不能直接推广到Markov系统中[25].此外,现有文献在进行Markov切换系统的丢包问题的研究时多基于H∞滤波器,而该方法计算量较大,难以满足实际应用中对时效性的要求.针对上述情况,本文对一类带丢包的Markov切换线性系统的状态估计问题进行了研究.

首先,利用一个转移概率已知的二态Markov链对系统是否丢包进行建模,将原来的单Markov链系统变为含有两个切换参数的双Markov链系统.然后,通过定义两个模型集的乘积集,将两个模型集进行融合,基于交互式多模型(IMM)算法的构架,以分层的方式对双Markov链系统进行滤波处理.最后,采用一种新的最优估计方法作为IMM框架中的主滤波方法对系统进行状态估计,并通过目标跟踪的仿真实例对该算法的有效性进行了验证.

2构造双Markov链系统

考虑如下的Markov切换线性系统

xk+1=Φ(αk)xk+Γ(αk)wk(αk)

(1)

zk=H(αk)xk+vk(αk)

(2)

其中,xk∈n为系统的状态向量,zk∈m为传感器产生的量测向量.αk为系统模型的切换参数,在M1={1,2,…,r1}中取值,{αk:k≥0}为离散时间齐次Markov链.模型之间的转移概率为≜分别为状态转移阵、系统噪声阵和观测阵.wk(αk)∈p,vk(αk)∈m分别为系统噪声和量测噪声.

设yk∈m为k时刻滤波器接收到的量测,则带丢包Markov切换系统的量测方程为

yk=βkzk+(1-βk)yk-1

(3)

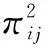
由式(1)～(3)可见,我们得到的系统为双Markov链系统,且切换参数αk与βk相互独立.

对式(1)～(3)所描述的系统做如下假设:

假设1wk(αk)和vk(αk)为相互独立的高斯白噪声,统计特性满足如下条件:

(4)

(5)

(6)

其中δkt为Kronecker-δ函数.

假设2系统的初始状态x0独立于系统噪声wk(αk)和量测噪声vk(αk),并且满足

E[x0]=μ0,E[(x0-μ0)(x0-μ0)Τ]=P0

(7)

3最优滤波算法

对式(1)～(3)所描述的系统进行状态估计时,一次滤波循环过程中不仅用到当前时刻的量测值,而且用到了上一时刻的量测值.因此,经典的Kalman滤波方法不再适用于该系统.为解决该问题,引入文献[26]中的状态增广的最优线性滤波算法,将上一时刻的量测向量扩充到状态方程中,对系统模型进行重构,得到形式类似于一般离散线性系统的系统方程和量测方程,在此基础上进行状态估计,具体方法如下.

将yk-1作为状态量,扩充到状态方程中,则式(1)～(3)可写为:

(8)

(9)

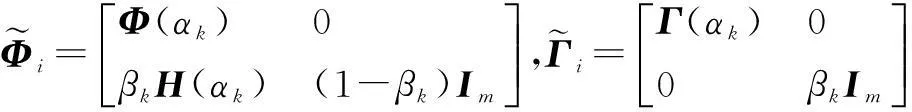
由假设1可知,

(10)

对于式(8)、(9)所描述的系统,在上述假设条件下,其模型条件下最优滤波方程如下(为简化符号,此处将i省略):

(11)

(12)

(13)

(14)

(15)

(16)

Lk=

(17)

(18)

(19)

该算法与标准Kalman算法不同之处在于,该算法中当前时刻的一步预测值是利用上一时刻的一步预测值进行递推计算,而标准Kalman算法中,当前时刻的一步预测值是利用上一时刻的估计值进行推算.当描述丢包情况的切换参数βk≡1时,即整个过程中无丢包现象发生,则b=1,此时滤波方程式(12)～(20)简化为标准Kalman滤波方程.

4带丢包Markov切换系统状态估计

本文基于交互式多模型算法的框架,利用文献[27]中处理闪烁噪声的思想对带丢包Markov切换系统进行滤波估计.

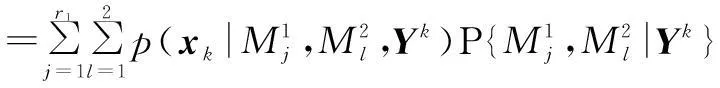
(20)

假设两个模型集之间相互独立,则乘积集的模型转移概率为

πhi≜P{Mk,i|Mk-1,h}

(21)

其中,h=2(g-1)+f;i=2(j-1)+l;h,i=1,2,…,2r1;g,j=1,2,…,r1;f,l=1,2.

由于模型集之间是相互独立的,因此基于IMM算法的构架对双Markov链系统进行状态估计时,其中的交互过程可以分层进行.

IMM算法框架下的带丢包Markov切换系统状态估计算法步骤如下:

(1)求交互概率

乘积集中的交互概率由各个模型集中对应模型的交互概率进行组合得到.

μk-1,h|i≜P{Mk-1,h|Mk,i,Yk-1}

(22)

其中,

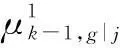
(23)

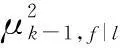
(24)

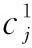
(2)输入交互

与经典的IMM算法相比,该步不再是对上一时刻各滤波器的滤波值进行交互,而是对当前时刻各滤波器的一步预测值进行交互,并且采用两层结构进行.

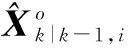
(25)

(26)

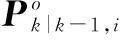
(27)

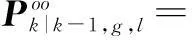
(28)

(3)模型条件滤波

将上一步得到的交互后的当前时刻的一步预测值作为对应滤波器的输入,各个滤波器之间并行滤.在该步中,不仅要得到当前时刻的滤波值和似然函数,还要计算得到下一时刻的一步预测值,用于下一次滤波循环的输入交互.

(29)

(30)

Qεk,i=b(1-b)[Hi-Im]qk,i[Hi-Im]Τ

(31)

(32)

(33)

(34)

(35)

(36)

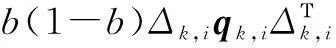
(37)

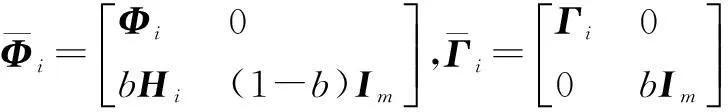
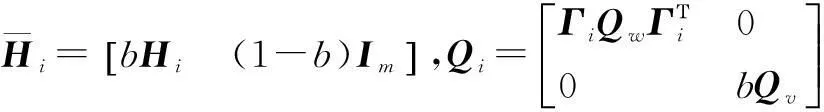
k时刻,各模型的似然函数为

Λk,i=p(yk|Mi,Yk-1)=N(εk,i;0,Qεk,i)

(38)

(4)模型概率更新

首先求解乘积集中各模型的模型概率.

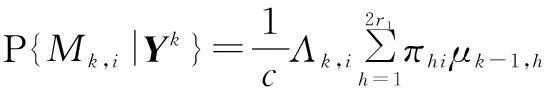
(39)

其中,c为标准化常量.然后利用求得的乘积集中的模型概率更新模型集M1和M2中各模型的模型概率.

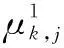
(40)

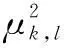
(41)

(5)输出组合

(42)

(43)

5仿真分析

采用类似于文献[28]中二维空间目标跟踪的仿真实例对本文提出的算法进行验证并与文献[22]中所提出的算法进行比较.

与本文不同之处在于,文献[22]中,当量测丢失时利用量测噪声作为当前时刻的量测值,在此基础上构造双Markov系统;此外,其核心算法为在线更新γ值的H∞滤波,仿真结果中将给出两种算法的滤波精度和计算复杂度的比较.

目标轨迹描述:在笛卡尔坐标系中,设目标的起始位置为[60km 40km],目标运动状态包括1s到60s以300m/s的速度进行非机动飞行;61s到155s以1.87°/s的转弯角速率进行180°的左转弯;156s到180s为非机动飞行;181s到245s以-2.8°/s的转弯角速率进行180°的右转弯;246s到300s为非机动飞行.

目标运动模型:采用Markov切换模型对该系统进行建模,系统模型为

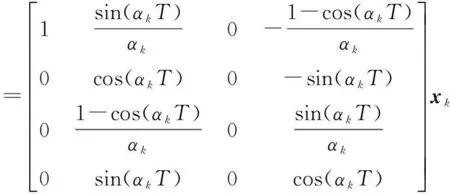
(44)

目标量测模型:可获得的量测值为带丢包的位置信息,采用二状态Markov链对是否丢包进行建模.

(45)

仿真结果通过100次Monte Carlo仿真实验得到,利用均方根误差(RMSE)对算法的性能进行评估.RMSE计算公式如下,其中,M为Monte Carlo仿真次数.

(46)

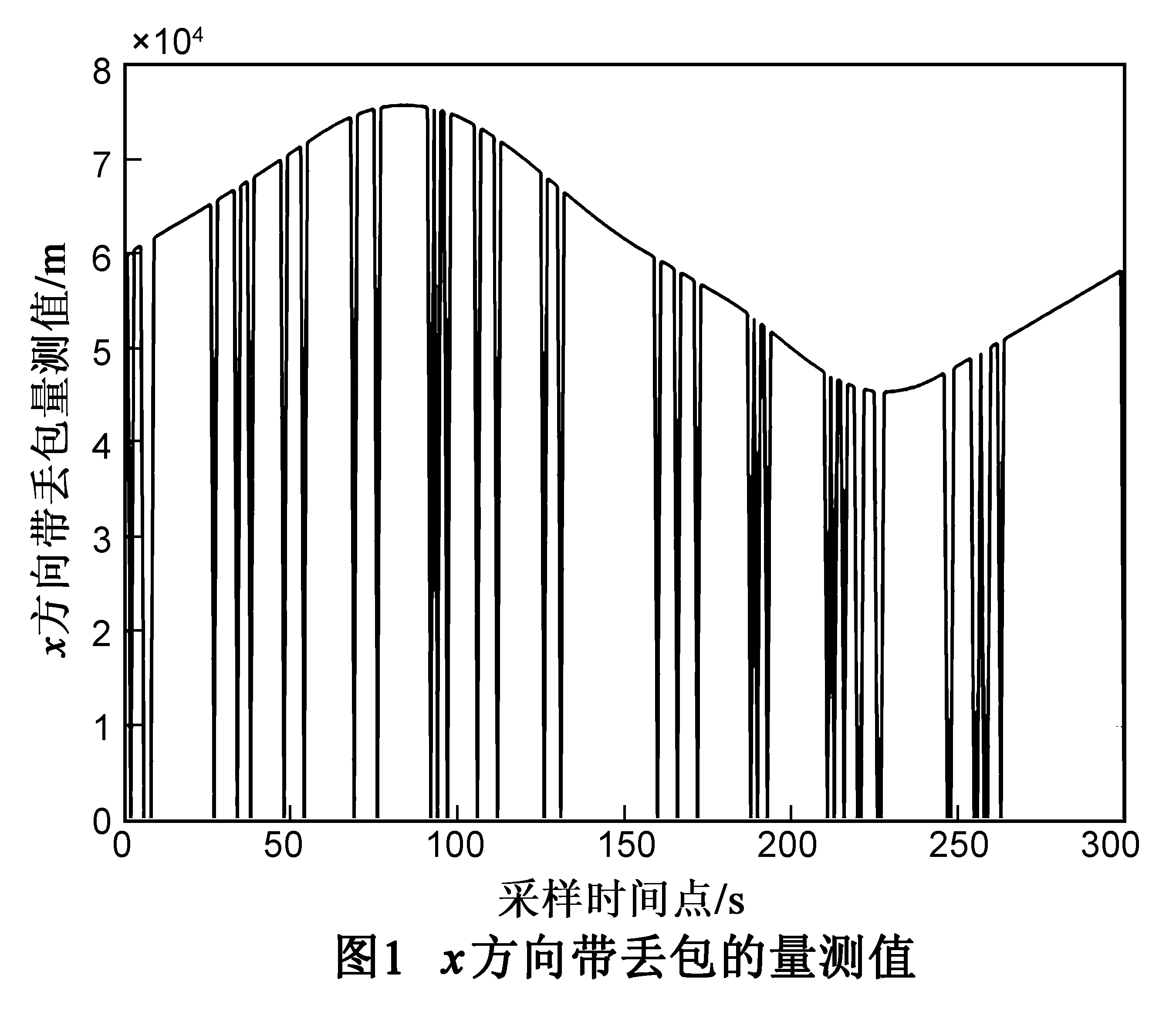
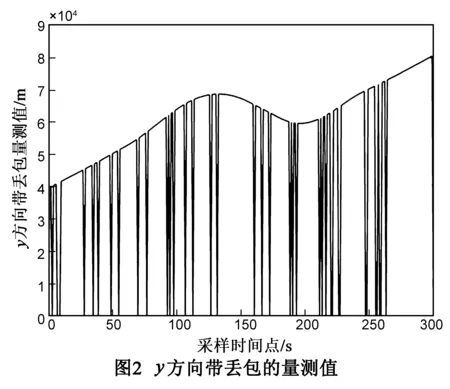
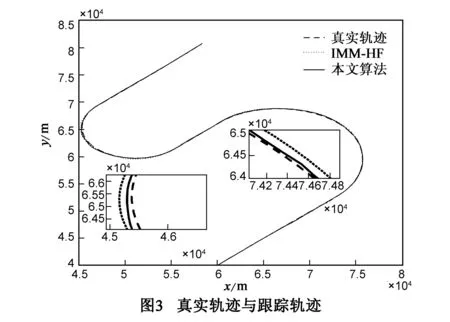
表1　算法运行时间统计表

IMM-HF本文算法运行时间(s)104.22517627.185750

图3为整个跟踪过程中,本文所提出的算法的跟踪轨迹与文献[22]中的算法的跟踪轨迹以及真实轨迹的比较.由仿真曲线可以看出,两种算法均能在量测发生丢失时对目标进行有效的跟踪.其中的局部放大图取自目标进行两次转弯时,可以看出,在目标进行机动转弯时,本文算法的跟踪轨迹与真实轨迹更加接近,说明本算法在高机动环境中较文献[22]中的算法的跟踪精度更高.

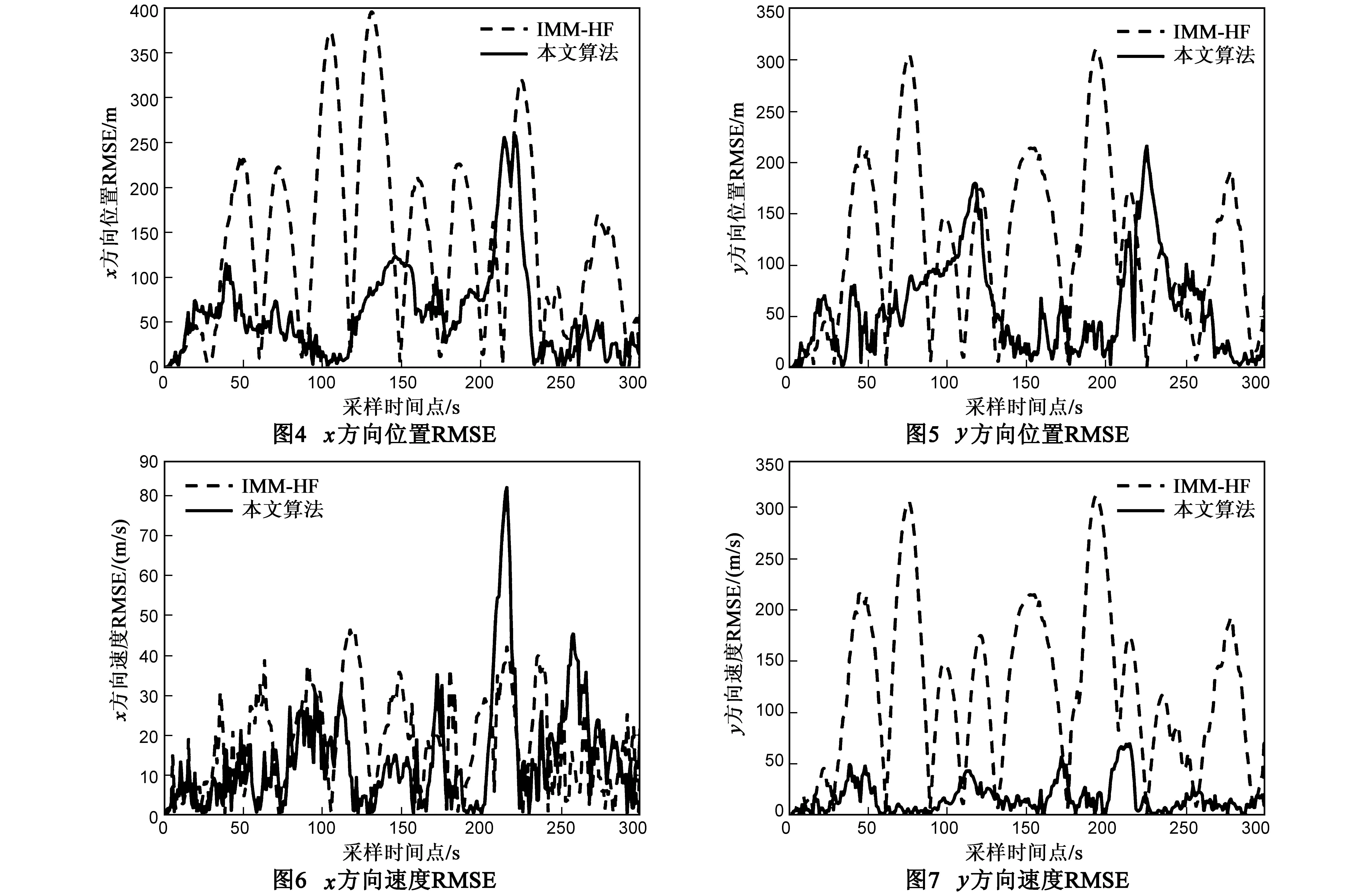
图4至图7为本文所提出算法与文献[22]中IMM-HF算法的跟踪精度比较.由仿真曲线可以看出,本文所提处算法除在220s至240s时间段内在y方向的位置跟踪精度以及x方向的速度跟踪精度低于IMM-HF算法外,其他时刻以及其他状态分量(x方向位置分量和y方向的速度分量)的所有时刻的跟踪精度均优于IMM-HF算法.

结合表1中两种算法的运行时间,可以看出,本文所提出的算法不仅滤波精度较高,而且计算量远远小于IMM-HF算法,更加有利于实际应用中对时效性的要求.

综合以上仿真结果,我们可以得出,本文中所提出的算法不仅可以在发生量测丢包时对目标进行有效、可靠的跟踪,而且计算复杂度较小,更加符合实际应用中对实时性的要求.

6结论

本文针对一类含有量测数据丢包的Markov切换系统的状态估计问题进行了研究.利用一个二态的Markov链对量测值是否发生丢包进行建模,得到双Markov切换系统,在此基础上,提出了一种含有双Markov切换参数的交互式多模型算法.该算法以经典的IMM算法为框架,通过定义乘积集以分层的方式对双Markov系统进行滤波处理,并且引入了新的估计方法来处理一次滤波循环中用到多个时刻量测值的问题.仿真实验证明,该算法在量测数据丢包情况下对目标运动状态的机动改变非常敏感,无论目标进行高机动的转弯运动或是平缓的直线运动,该算法均可在量测数据不完全的条件下对目标进行可靠、有效的跟踪.此外,该算法的计算复杂度较小,实时性高.由此可以得出,该算法具有较高的可行性和较大的实用价值.

参考文献

[1]丁玉才.时滞Markov跳跃系统的性能分析及滤波问题研究[D].四川成都:电子科技大学,2013.

[2]Li X R,Jilkov V P.Survey of maneuvering target tracking.Part V.Multiple-model methods[J].IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1255-1321.

[3]Ji Y,Chizeck H J.Controllability,stabilizability,and continuous-time Markovian jumping linear quadratic control[J].IEEE Transactions on Automatic Control,1990,35(7):777-788.

[4]Feng X,Loparo K A,Ji Y,Chizeck H J.Stochastic stability properties of jump linear systems[J].IEEE Transactions on Automatic Control,1992,37(1):1884-1892.

[5]Fang Y,Loparo K A.Stochastic stability of jump linear systems[J].IEEE Transactions on Automatic Control,2002,47(7):1204-1208.

[6]Costa O L V,Fragoso M D.Stability results for discrete-time linear systems with Markovian jumping parameters[J].Journal of Mathematical Analysis and Applications,1993,179(1):154-178.

[7]Costa O L V.Linear minimum mean squares error estimation for discrete-time Markovian jump linear systems[J].IEEE Transactions on Automatic Control,1994,39(8):1685-1689.

[8]Shi P,Boukas E K,Agarwal R K.Kalman filtering for continuous-time uncertain systems with Markovian jumping parameters[J].IEEE Transactions on Automatic Control,1999,44(8):1592-1597.

[9]Wang A,Lam J,Liu X.Nonlinear filtering for state delayed systems with Markovian switching[J].IEEE Transactions on Signal Processing,2003,51(9):2321-2328.

[10]赵燕.非线性系统中时滞及丢包问题的模糊控制研究[D].黑龙江哈尔滨:哈尔滨工业大学,2010.

[11]Sinopoli B,Schenato L,Franceschetti M,Poolla K,Jordan M I,Sastry S S.Kalman filtering with intermittent observations[J].IEEE Transactions on Automatic Control,2004,49(9):1453-1464.

[12]Epstein M,Shi L,Tiwari A,Murray R M.Probabilistic performance of state estimation across a lossy network[J].Automatica,2008,44(12):3046-3053.

[13]Ma J,Sun S L.Optimal linear estimation for systems with random sensor delays,multiple packet dropouts and uncertain observations[J].IEEE Transactions on Signal Processing,2011,59(11):5181-5192.

[14]Ma J,Sun S L.Distributed fusion filter for multi-sensor systems with random sensor delay,multiple packet dropouts and uncertain observations[A].Proceedings of the 15th International Conference on Information Fusion[C].Singapore:IEEE,2012.1036-1043.

[15]Ma J,Sun S L.Centralized fusion estimators formulti-sensor systems with random sensor delays,multiple packet dropouts and uncertain observations[J].IEEE Sensor Journal,2013,13(4):1228-1235.

[16]马静,孙书利.带有随机时滞、丢包和不确定观测系统的次优融合估计[A].第32届中国控制会议论文集[C].西安:IEEE,2013.4553-4558.

Ma J,Sun S L.Suboptimal fusion estimation for systems with random delay,packet dropout and uncertain observation[A].Proceedings of the 32nd Chinese Control Conference[C].Xi′an,China:IEEE,2013.4553-4558.(in Chinese)

[17]Moayedi M,Foo Y K,Adaptive Kalman filtering in networked systems with random sensor delays,multiple packet dropouts and missing measurements[J].IEEE Transactions on Signal Processing,2010,58(3):1577-1588.

[18]郭戈,王宝凤.多丢包不确定离散系统的鲁棒Kalman滤波[J].自动化学报,2010,36(5):767-772.

Guo G,Wang B F.Robust Kalman filtering for uncertain discrete-time systems with multiple packet dropouts[J].Acta Automatica Sinica,2010,36(5):767-772.(in Chinese)

[19]Dong H L,Wang Z D.Robust H∞ filtering for a class of nonlinear networked systems with multiple stochastic communication delays and packet dropouts[J].IEEE Transactions on Signal Processing,2010,58(4):1957-1966.

[20]Ma L,Da F P,Zhang K J.Exponential H∞ filter design for discrete time-delay stochastic systems with Markovian jump parameters and missing measurements[J].IEEE Transactions on Circuits and Systems,2011,58(5):994-1007.

[21]You J,Yin S,Yu Z D.Robust estimation for discrete time-delay Markov jump systems with sensor non-linearity and missing measurements[J].IET Control Theory and Applications,2013,8(5):330-337.

[22]Li W L,Jia Y M,Du J P,Zhang J.Robust state estimation for jump Markov linear systems with missing measurements[J].Journal of the Franklin Institute,2013,350:1476-1487.

[23]Blom H A P,Bloem E A.Tracking multiple maneuvering targets from possibly unresolved,missing or false measurements[A].Proceedings of the 7th International Conference on Information Fusion[C].Chicago:IEEE,2005.323-330.

[24]Dong H L,Wang Z D,Gao H J.Distributed H∞ filtering for a class of Markovian jump nonlinear time-delay systems over lossy sensor networks[J].IEEE Transactions on Industrial Electronics,2013,60(10):4665-4672.

[25]王国良.若干类马尔科夫切换系统的控制与滤波[D].辽宁沈阳:东北大学,2009.

[26]Sun S L,Xie L H,Xiao E D,Soh Y C.Optimal linear estimation for systems with multiple packet dropouts[J].Automatica,2008,44(5):1333-1342.

[27]Daeipour E,Bar-Shalom Y.IMM tracking of maneuvering targets in the presence of glint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(3):996-1003.

[28]Jilkov V P,Angelova D S,Semerdijev T A.Design and comparison of mode-set adaptive IMM for maneuvering target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(1):343-350.

周卫东男,1966年生于江苏宜兴,现为哈尔滨工程大学教授、博士生导师.主要研究方向为组合导航、信息融合及容错技术.

E-mail:zhouweidong@hrbeu.edu.cn

刘萌萌(通讯作者)女,1989年生于山东青岛,现为哈尔滨工程大学自动化学院博士研究生.主要研究方向为多模型信息融合和马尔可夫跳变系统.

E-mail:liumengmeng89@126.com

State Estimation for Jump Markov Linear Systems with Packet Dropouts

ZHOU Wei-dong,LIU Meng-meng

(CollegeofAutomation,HarbinEngineeringUniversity,Harbin,Heilongjiang150001,China)

Abstract:This study is devoted to the state estimation problem for a class of jump Markov linear systems with packet dropouts.The behavior of packet dropouts is described by a two-state (i.e.,packet-dropping and normal) Markov chain with known transition probability matrix,which is independent of the system dynamics.Therefore,the obtained system can be modeled as a jump Markov linear system with two switching parameters.A product set is defined to combine the two mode sets and the corresponding relationship between models in the product set and models in the individual mode set is given.Based on the product set,we cast the model into the framework of the interacting multiple model (IMM) algorithm and the filtering steps are carried out in a layered manner.Furthermore,an optimal estimation algorithm is combined with the IMM to obtain the filtering results of the system.A maneuvering target tracking example is presented to prove the effectiveness of the proposed algorithm.

Key words:jump Markov linear system;packet dropouts;double Markov chains;optimal estimation algorithm;interacting multiple model algorithm

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.023

中图分类号:TN 911.23

文献标识码：A

文章编号：0372-2112 (2016)03-0646-07

基金项目:国家自然科学基金(No.61102107,No.61374208)

收稿日期:2014-09-23;修回日期:2015-01-08;责任编辑:覃怀银