应用于多源SAR图像匹配的级联SIFT算法

王　峰,尤红建,傅兴玉,许　宁,3

(1.中国科学院电子学研究所,北京 100190;2.中国科学院空间信息处理与应用系统技术重点实验室,北京 100190;

3.中国科学院研究生院,北京 100190)



应用于多源SAR图像匹配的级联SIFT算法

王峰1,2,尤红建1，2,傅兴玉1,2,许宁1,2,3

(1.中国科学院电子学研究所,北京 100190;2.中国科学院空间信息处理与应用系统技术重点实验室,北京 100190;

3.中国科学院研究生院,北京 100190)

摘要：针对多源SAR(Synthetic Aperture Radar)图像几何精处理需要大量离散控制点的问题,文章中提出一种级联SIFT(Scale Invariant Feature Transform)匹配算法.首先,采用大尺度自适应各向异性高斯SIFT(Adapted Anisotropic Gaussian-SIFT,AAG-SIFT)算法进行图像粗配准,大尺度AAG尺度空间可以在模糊不稳定局部纹理干扰的同时,保持图像的结构信息,提高算法的鲁棒性;其次,级联一种局部SIFT匹配算法,在粗配准后图像间进行局部匹配,避免不相关区域内重复纹理对特征匹配的影响;最后,通过尺度和旋转等先验条件筛选匹配点对,保证匹配结果的准确性.对比实验表明,级联SIFT处理可以增加提取同名点的数量和空间分布质量,而且匹配点定位准确.

关键词:多源SAR图像匹配;级联SIFT;AAG-SIFT;局部匹配

1引言

多源SAR匹配是综合运用不同SAR图像,全面反映地物信息的前提,是实现遥感数据融合、拼接、变化检测等过程的关键步骤.由于多源SAR数据的成像条件不同,图像间存在较为复杂的几何和辐射差异,常用的图像匹配方法的效果不理想,算法的鲁棒性和匹配结果的准确度很难同时保证.

现阶段,基于SIFT[1]算法的同名点提取方法成为SAR图像匹配的研究热点.SIFT算法具有尺度和旋转不变性,是计算机视觉领域公认的区分能力很强的特征匹配算法.文献[2]分析了SIFT算法应用于SAR图像匹配时的检测子性能,提出SIFT-OCT算法,去除受噪声干扰严重的低尺度特征点,提高了匹配鲁棒性和效率.近年来,各向异性尺度空间的提出明显提升了图像匹配算法的性能.Alcantarilla等[3]提出KAZE特征进行特征匹配,在各向异性尺度空间检测和描述特征点,具有更好的区分性和准确性,在自然场景匹配中获得了很好的性能.王山虎等[4]根据双边滤波与热扩散方程的相似性,提出了基于双边滤波器建立各向异性尺度空间的BFSIFT算法,有效地增加了同名点提取数量.文献[5]中提出根据图像局部结构特征,自适应建立各向异性高斯尺度空间,在去除噪声干扰的同时,保持图像的结构信息,可以获得更加稳健的特征,增加了获得匹配点对的数量和定位精度.基于各向同性尺度空间的SIFT算法全面描述图像局部信息,得到的局部特征稳定且定位精度高,具有较好的运算效率,但是特征区分度不足,算法的鲁棒性较差.基于各向异性尺度空间的SIFT算法,更加注重局部结构信息的描述,有效地提高了算法的鲁棒性,但是算法对大场景数据计算耗时较多.

针对上述问题,本文提出级联SIFT匹配算法,通过级联两类配准算法,综合两类算法的优势.首先,运用大尺度自适应各向异性高斯SIFT算法实现图像的粗配准;其次,针对粗配准后的图像,级联局部SIFT匹配算法,在图像的局部区域内进行特征匹配,高效地获得定位准确的匹配结果.

2级联SIFT匹配算法

级联SIFT匹配算法,采用由粗到细的实现策略,通过级联两类SIFT匹配算法实现.首先,利用AAG-SIFT算法实现图像的粗配准,获得图像间整体几何变换关系,保证算法的鲁棒性;其次,针对粗配准后图像,在局部对应区域内比较SIFT特征的相似性,去除不相关区域的干扰,明显提高匹配点对数量;最后,通过特征的主方向和尺度参数进行筛选,保证匹配结果的准确性.整体算法流程如图1中所示.

2.1SIFT算法简介

SIFT算法主要分为3个部分[1]:(1)构建尺度空间;(2)检测特征点,生成描述符;(3)特征匹配.

首先,通过方差不断增大的高斯函数与图像卷积,可建立图像的尺度空间表达:

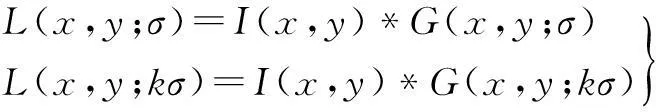
(1)

其中,L(x,y,σ)为高斯尺度空间,I(x,y)为原图像,G(x,y,σ)为标准差为σ的高斯函数,k为尺度变化量,*代表卷积运算.建立图像的尺度空间后,采用高斯拉普拉斯算子(LoG)检测图像中的极值点,并用高斯差分尺度空间(DoG)近似,其表达式为:

D(x,y,σ)=L(x,y,kσ)-L(x,y,σ)

(2)

其中,D(x,y,σ)为高斯差分尺度空间.

其次,在尺度空间中检测极值点,去除低对比度的不稳定点,得到最终的特征点.对检测到的特征点,统计邻域梯度方向直方图,确定主方向,旋转邻域到水平方向,统计分块梯度方向直方图,生成128维描述子.

最后,利用描述子间欧式距离建立匹配对,通过RANSAC(RANdom SAmple Consensus)[6]算法筛选出正确匹配点.

2.2自适应各向异性高斯尺度空间

高斯尺度空间是一种简单的尺度空间,但不是唯一的尺度空间表示[3].高斯滤波核函数不能保持目标结构,纹理细节和图像噪声都会被同样模糊处理,而且它只能拟合圆形目标,对实际场景中大量存在的具有一定方向性和扁曲率的目标拟合效果很差.另外,随着滤波尺度的增加,图像模糊程度增加,控制点的定位精度降低.自适应各向异性高斯滤波器克服了高斯尺度空间的上述不足,其在模糊图像噪声干扰的同时,可以保持图像的边缘纹理信息,因此,各向异性高斯尺度空间提取的特征对图像噪声干扰的鲁棒性和稳定性更佳[5].

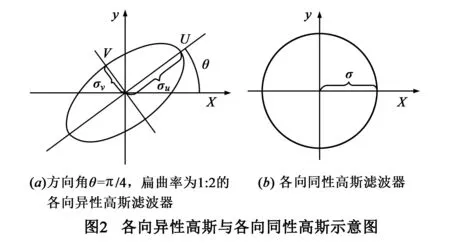
各向异性高斯滤波器的一般表示为[7]:

gθ(u,v;σu,σv,θ)=

(3)

其中,*表示卷积运算,θ代表滤波器的方向,σu和σv分别表示u轴和v轴方向的尺度参数,u轴与水平方向夹角为θ,v轴垂直于u轴,并且有:

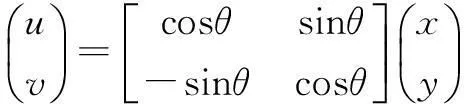
(4)

相比于普通的高斯滤波器,各向异性高斯增加了空间旋转角度θ和两个尺度参数σu、σv(如图2所示),可以更好地拟合局部结构.空间旋转角度θ对应边缘方向,以待滤波点为中心建立采样邻域窗口,统计窗口内采样点的梯度方向直方图,以空间高斯模板和梯度幅值为权重对梯度方向加权,可以消弱噪声影响.直方图最大峰值对应的方向就对应了局部梯度的垂直方向,因此,各向异性高斯的空间旋转角度θ对应梯度直方图最大峰值角度的垂直方向.

第o组s层各向异性高斯滤波器的长轴尺度设置与原始高斯滤波器相同,如式(5)所示:

σu=σ(o,s)=σ02(o+s)/S,o∈[0,…,O-1],

s∈[0,…,S-1]

(5)

其中,σo是滤波器的基本尺度参数,O和S分别代表尺度空间的组数和层数,o和s分别表示当前组和层的标号.短轴尺度由图像的局部二阶矩矩阵决定,局部二阶矩矩阵常用来拟合图像的局部结构形状[8,9].点P(x0,y0)附近σ尺度的二阶矩矩阵M定义如下式所示:

(6)

其中Ix和Iy表示点(x,y)处x和y方向的偏导数,σ对应滤波器的当前滤波尺度σ(o,s).权重参数wσ(x,y)是空间高斯滤波函数:

(7)

二阶矩矩阵的特征值表征局部像素的结构形状,有三种情况[8]:

(1)当一个特征值大,另一个较小时,对应边缘区域;

(2)当两个特征值都较小时,对应平坦的匀质区域;

(3)当两个特征值都较大时,对应角点区域.

根据图像的统计特性描述局部区域的各向异性程度可以定义为[9]:

(8)

其中λmax(M)表示较大的特征值,λmin(M)表示较小的特征值.因此,我们根据局部区域的各向异性程度确定各向异性高斯滤波器的形状如下式所示:

σv=σu*γn

(9)

通过实验验证,推荐指数参数n=1/3[5].通过局部区域二阶矩矩阵自适应调节滤波器的扁曲程度,可以很好的拟合图像局域区域的结构特性:在均匀区域,σv≈σu,具有圆滤波器的模糊效果;在边缘区域,扁曲程度增加,具有较好的边缘保持效果.

2.3大尺度空间的构建

在原始分辨率处理SAR图像,容易受到局部纹理的干扰,这种干扰的来源主要包括斑点噪声和成像条件两个方面.例如不同时相下河岸线的变化,不同视角条件下建筑物位置的偏移,不同极化方式导致的局部纹理差异,都会影响特征的匹配.但是在大尺度观察图像,图像主要呈现的是图像的整体结构信息,稳定性好,图像噪声对局部纹理的干扰降低[2].如图3所示,从大尺度图像上观察,湖泊的形状以及城市间道路的方向等图像的全局结构表征是稳定的,但是在低尺度图像上,局部细节明显不同.因此,在大尺度空间检测和描述特征,可以提高算法的鲁棒性[4].

另一方面,各向异性高斯尺度空间的构建,计算量较大[3,4],而提高尺度空间的尺度,可以降低待处理图像的尺寸,提高计算效率.虽然随着尺度空间的增加,滤波器滤波参数变大,图像的模糊程度增加,会部分降低提取特征点的定位精度,但是部分特征精度的降低不会影响图像整体的粗配准过程.因此,我们采用在大尺度构建AAG尺度空间,获得AAG-SIFT特征.

对获得的大尺度AAG-SIFT特征进行匹配,通过RANSAC算法获得图像间的刚体变换关系[6],然后校正图像,就可以实现图像的粗配准,刚体变换模型如下式所示:

(10)

其中,(x,y)和(u,v)表示两幅图像的坐标,λ是图像间的尺度参数,θ是图像间的旋转角度,(x0,y0)表示图像间的整体平移量.

2.4局部SIFT匹配算法

通过大尺度AAG-SIFT算法实现图像的粗配准,去除图像整体间的尺度和旋转差异.根据粗配准的先验信息,在图像局部进行图像匹配,可以减少计算量.另一方面,局部匹配仅在图像局部相关区域搜索匹配点对,去除其他区域中重复场景的干扰,保证匹配结果的正确性,因此,可以获得更多准确的匹配点对.考虑到粗配准已经去除了待匹配图像间的尺度差异,图像处于同样的尺度条件下,因此,可以只构建一组尺度空间进行局部图像匹配.也就是说,局部SIFT匹配算法只构建组数o=0的高斯尺度空间,然后生成SIFT特征.

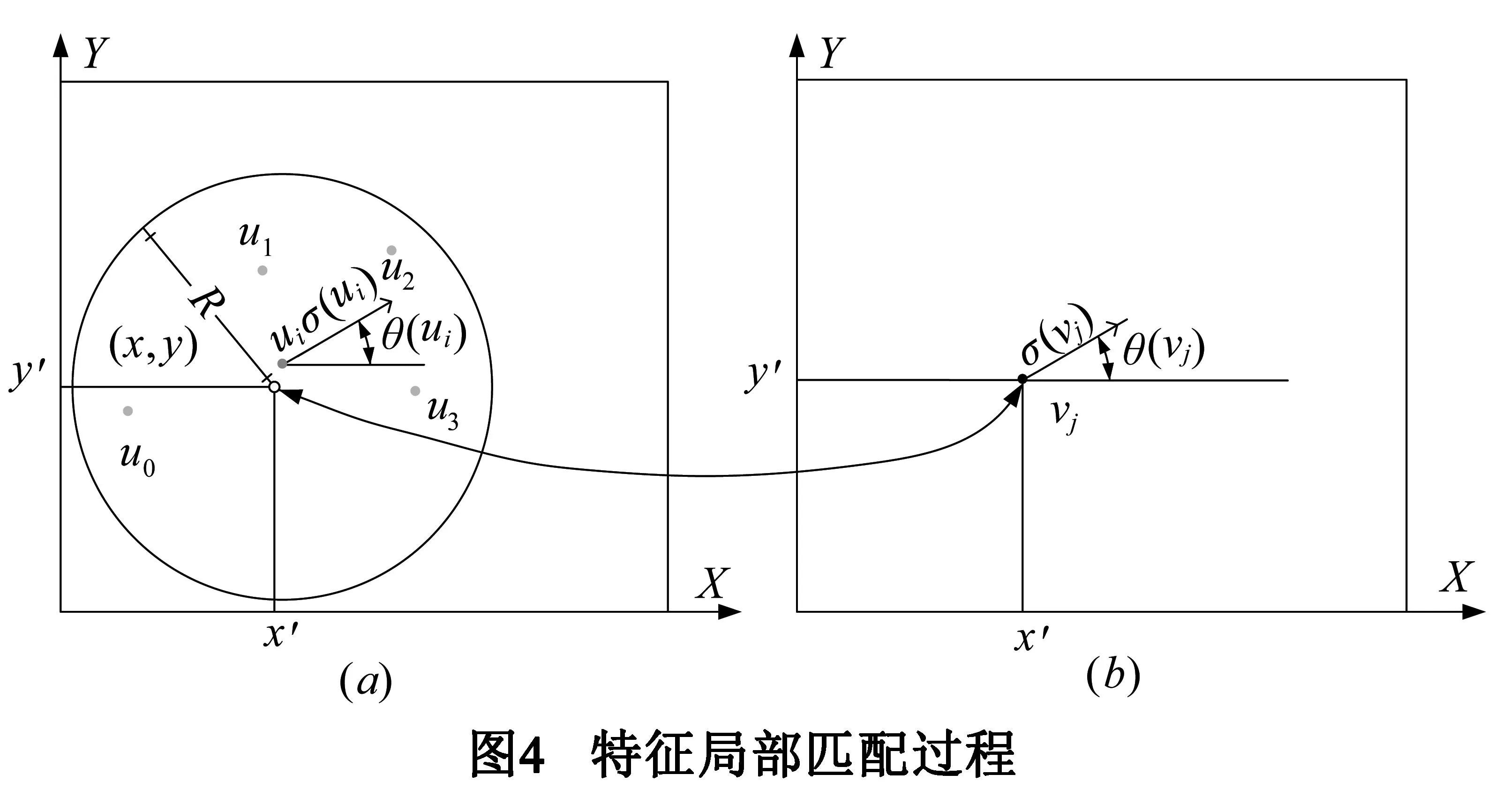
粗配准后的图像间,同名点对间只存在局部范围内的平移,如图4所示.ui(x,y)和vj(x′,y′)分别表示两幅图像中的第i个和第j个特征向量,(x,y)和(x′,y′)分别表示这两个特征点的坐标,假设空间搜索范围半径为R,则对于图4(b)中特征vj(x′,y′)的局部空间限制可以表示为:

ui(x,y):(x-x′)2+(y-y′)2≤R2

(11)

图4(a)中,以点(x′,y′)为圆心,R为半径圆区域内可以找到符合式(11)空间限制的一系列待匹配特征点u0,…,u3,ui.计算这些待匹配特征向量与特征向量vj的相似性,如下式所示:

(12)

其中,|*|2表示计算向量的二范数,Td表示特征向量相似性阈值.在搜索范围R内,特征向量间最小距离小于阈值Td,则特征vj(x′,y′)的最佳匹配特征为ui(x,y).为了保证匹配的正确性,这里采用双向匹配策略:假设以特征ui(x,y)为基准局部匹配得到的最佳匹配特征为vj(x′,y′),相应地,要求以vj(x′,y′)为基准的局部匹配得到的最佳匹配特征也必须是ui(x,y),才能认定特征ui(x,y)和vj(x′,y′)是最佳匹配的.

除了特征向量,SIFT特征还具有主方向和尺度参数.由于图像间已经去除了整体尺度和旋转差异,对应匹配点对的主方向角度和尺度参数差异应该在一定范围内.因此,我们可以通过特征主方向和尺度参数进一步筛选匹配点对,保证匹配结果的准确性.特征主方向限制可以表示为:

(13)

其中,θ(ui)和θ(vj)分别表示特征的主方向,Tθ表示特征主方向角度偏差阈值.特征尺度参数限制可以表示为:

(14)

其中,σ(ui)和σ(vj)分别表示特征对应的尺度参数,计算公式见式(5),Tσ表示特征尺度参数偏差阈值.

3多源SAR图像匹配对比实验

为了测试本文算法的性能,分别基于机载和星载SAR图像,与常用的OCT-SIFT[2]以及BF-SIFT[4]算法进行对比实验.本文算法参数设置如下:大尺度AAG-SIFT尺度空间o=2～4,局部SIFT尺度空间o=0,空间搜索半径R=50,特征向量相似性阈值Td=100000,主方向旋转角度偏差阈值Tθ=10°,尺度参数偏差阈值Tσ=1.3.实验对比准则包括:

(1)匹配点数量:

由于SAR图像的成像特点,不同成像条件下的图像会存在局部几何畸变,需要在图像局部处理,更多的匹配点对更利于图像局部的精处理.

(2)匹配点空间分布质量:

控制点的离散分布对于图像的精确处理具有重要的意义,文献[10]中尝试用不同数量和分布的控制点对遥感图像进行配准,发现配准精度不仅取决于同名点的数目,而且与同名点的分布质量有重要的关系.描述控制点分布离散性的分布质量公式见式(15):

(15)

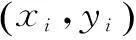
(16)

3.1不同视角机载SAR实验

本组实验中选取两幅机载X波段不同视角的长治郊区图像,拍摄时间分别为2010年12月4日和7日.匹配结果见图5,右图获取的视角较小,距离向压缩明显.图5(a)～5(c)中分别展示了不同算法在原始图像上的匹配结果,图5(d)中展示了在粗配准后的图像上,局部SIFT匹配的结果.几种匹配算法提取匹配点数以及匹配结果空间分布质量如表1所示.

对比实验结果可以看出,本文中提出的级联变换SIFT匹配算法提取匹配点数最多,而且匹配点的空间分布质量最好.常用的SIFT-OCT和BFSIFT算法的尺度空间是由1～3组尺度构成,在降采样后图像进行图像匹配,而局部SIFT算法在原始分辨率图像构成尺度空间,因此,级联SIFT算法可以提取更多的特征点,并保证了最终获得匹配点的数量.另一方面,级联SIFT算法采用局部匹配策略,匹配过程在局部区域内进行,去除了图像其他区域的相似纹理对匹配结果的干扰,大大提高了获得图像匹配点对的数量.SIFT-OCT和BFSIFT算法获得的预匹配点对,需要通过RANSAC算法进行筛选.RANSAC算法假设图像间符合一定的几何模型,常用的几何模型有仿射变换模型和刚体变换模型,这种图像间几何模型的假设限制了控制点的几何分布,而且不能应对图像间的局部几何畸变问题.在级联SIFT匹配算法中,图像的粗配准为局部匹配算法提供了先验几何限制,因此,局部最佳匹配结果可以作为全局最佳匹配位置.特征向量相似性、特征主方向一致性以及特征尺度参数的筛选进一步确保匹配结果的正确性.不假设图像间的几何模型关系,使得级联SIFT算法能获得更好的匹配点对空间分布质量,更适用于处理存在局部几何畸变的SAR图像数据.

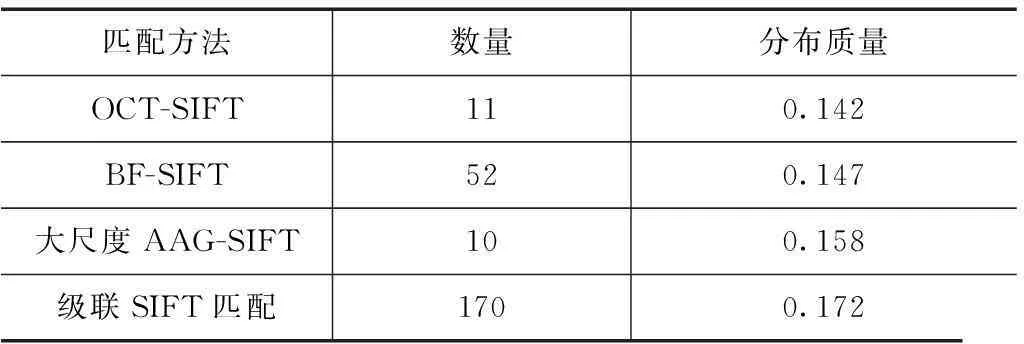
表1　不同视角影像间同名点提取结果

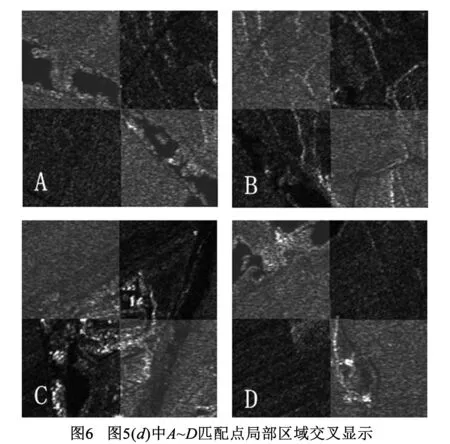
图6展示了图5(d)中矩形框标示的4对匹配点附近区域的交叉显示图.从图中可以看出,同名点附近纹理过渡平滑,河流、道路、山脊等明显地物结构特征连续,匹配点定位准确.

3.2不同传感器星载SAR实验

本部分实验选取两幅来自TerraSAR-X和Cosmo的星载数据,图像经过正射校正,都是HH极化方式,图像的空间分辨率分别是2.5m和3.0m.表2中列出了不同匹配算法得到的同名点数量和空间分布质量.

从表中看出,级联SIFT算法明显地提高了提取的匹配点对数量,而且控制点的空间分布质量最佳.图7中展示了不同算法得到的匹配结果,从图中可以看出,由于数据来自不同传感器,同一地物的辐射差异明显,匹配难度较大.级联SIFT算法能找到数量最多的同名点,而且控制点遍布图像的各个区域,分布质量最好,为后续图像精处理提供了有力的依据.

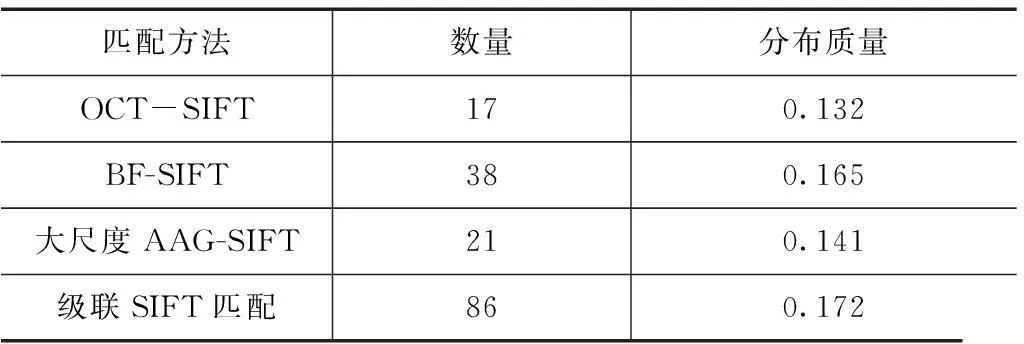
表2　不同传感器影像间同名点提取结果

图8展示了图7中标注的4个典型匹配点对附近区域的交叉显示结果.相同地物在不同图像中的表征变化明显,图像间存在明显的辐射差异性,匹配难度较大.通过级联SIFT算法获得的匹配点对,地物的结构特征过度平滑,定位精度高.局部SIFT匹配是由组数o=0的尺度构成,图像模糊程度最低,特征点的定位精度最高.同时,局部匹配算法充分利用了图像间已知的几何关系,在图像局部比较相似性,图像的不相关区域不会对匹配结果产生干扰,而特征向量的相似性、方向性和尺度参数限制,保证了匹配结果的准确性.

4结论

文章针对多源SAR图像匹配问题,提出一种级联SIFT匹配算法.首先通过大尺度AAG-SIFT算法实现图像的粗配准,然后采用局部SIFT匹配算法获得大量离散分布的匹配点对.算法可以应用于不同场景下的多源SAR图像间的匹配,大尺度AAG-SIFT算法通过在大尺度构建各向异性尺度空间,保证算法鲁棒性;局部SIFT匹配算法在低尺度空间获得大量特征点,定位精度高,同时充分利用预知几何先验筛选匹配结果,保证匹配结果的准确性.与已有的SIFT-OCT和BFSIFT算法相比,本文提出的算法有效地增加了获得匹配点的数量和分布质量.

参考文献

[1]Lowe DG.Distinctive image features from scale-invariant keypoints[J].International journal of computer vision,2004,60(2):91-110.

[2]Schwind P,Suri S,Reinartz P,et al.Applicability of the SIFT operator to geometric SAR image registration[J].International Journal of Remote Sensing,2010,31(8):1959-1980.

[3]Alcantarilla PF,Bartoli A,Davison AJ.KAZE features[A].Computer Vision—ECCV 2012[C].Firenze:Springer.214-227.

[4]Wang S,You H,Fu K.BFSIFT:A novel method to find feature matches for SAR image registration[J].Geoscience and Remote Sensing Letters,IEEE,2012,9(4):649-653.

[5]Wang F,You H,Fu X.Adapted anisotropic gaussian SIFT matching strategy for SAR registration[J].Geoscience and Remote Sensing Letters,IEEE,2015,10(3):573-577.

[6]Fischler MA,Bolles RC.Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J].Communications of the ACM,1981,24(6):381-395.

[7]Geusebroek J-M,Smeulders AW,Van De Weijer J.Fast anisotropic gauss filtering[J].Image Processing,IEEE Transactions on,2003,12(8):938-943.

[8]Harris C,Stephens M.A combined corner and edge detector[A].Fourth Alvey Vision Conference[C].Manchester,UK:AVC,1988,147-151.

[9]Mikolajczyk K,Schmid C.Scale & affine invariant interest point detectors[J].International journal of computer vision,2004,60(1):63-86.

[10]Zhu Q,Wu B,Xu Z.Seed point selection method for triangle constrained image matching propagation[J].Geoscience and Remote Sensing Letters,IEEE,2006,3(2):207-211.

王峰男,1988年出生于山东省日照市,现工作于中国科学院电子学研究所,博士,主要研究方向为多源遥感图像配准处理.

E-mail:wfeng-gucas@126.com

Cascade SIFT Matching Method for Multi-Source SAR Images

WANG Feng1,2,YOU Hong-jian1,2,FU Xing-yu1,2,XU Ning1,2,3

(1.InstituteofElectronics,ChineseAcademyofSciences,Beijing100190,China;2.KeyLaboratoryofTechnologyinGeo-spatialInformationProcessingandApplicationSystem,InstituteofElectronics,ChineseAcademyofSciences,Beijing100190,China;3.GraduateSchool,ChineseAcademyofSciences,Beijing100190,China)

Abstract:This paper presents a cascade SIFT matching method to get large numbers of discrete distributed matches for accurate procedure of multi-source SAR images.Firstly,to obtain more robust matching result,a large scale adapted anisotropic Gaussian scale-invariant feature transform (AAG-SIFT) method is proposed.It is constructed based on large scale AAG scale space,where unstable local textures are blurred,but the structures remain unaffected.Secondly,a local SIFT matching method is recommended which extracts SIFT features from the coarse registered images.And then the features are matched in the local regions to avoid the interferences of the repeated textures from uncorrelated regions.Finally,the priori condition of scale and rotation consistency is used to filter matches,guaranteeing the accuracy of the matching results.Compared with traditional matching methods,the proposed method increases the number and distribution quality of the matches,and the location of the matches is accurate.

Key words:multi-source SAR images matching;cascade SIFT;AAG-SIFT;local matching

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.008

中图分类号:TN957.52

文献标识码：A

文章编号：0372-2112 (2016)03-0548-07

收稿日期:2014-10-20;修回日期:2015-07-06；责任编辑：梅志强

E-mail：luoying2002521@163.com