基于环境扰动模型的干扰抑制极化滤波器性能研究

任　博,施龙飞,王国玉

(1.国防科技大学电子信息系统复杂电磁环境效应国家重点实验室 湖南长沙 410073;

2.国防科学技术大学电子科学与工程学院 湖南长沙 410073)



基于环境扰动模型的干扰抑制极化滤波器性能研究

任博1,2,施龙飞1,2,王国玉1,2

(1.国防科技大学电子信息系统复杂电磁环境效应国家重点实验室 湖南长沙 410073;

2.国防科学技术大学电子科学与工程学院 湖南长沙 410073)

摘要：具有双极化接收能力的雷达利用极化滤波手段能够抑制波束主瓣内的干扰信号.然而多径等传播环境效应会对干扰信号的极化特性产生扰动,影响实际接收信号的极化度,同时影响极化滤波器的干扰抑制性能.本文基于工程中对干扰抑制极化滤波器性能分析的需求,分别在理想条件及环境扰动条件下建立了用于描述干扰抑制极化滤波器性能的数学模型,仿真分析了极化滤波器的干扰抑制性能同干噪比、干扰极化状态以及环境扰动系数间的关系.随后为改善环境扰动影响下干扰抑制性能,提出了一种新的基于天线主辅阵联合的极化滤波的方法.最后通过极化雷达抗干扰实验不仅验证了极化滤波器性能表征模型的正确性,同时还在环境扰动条件下对比了两种滤波器性能,结果表明新的滤波方法在该扰动条件下干扰抑制方面的优势.

关键词:极化滤波;极化度;环境扰动模型

1引言

随着雷达极化理论技术的快速发展和器件水平的不断提高,极化滤波在抗干扰领域的应用愈发广泛[1，2].对于具有正交双极化同时接收能力的雷达,已被证明采用极化滤波手段能够有效抑制天线主波束内的压制干扰信号[3，4].随着自卫式干扰、随队式干扰等压制干扰样式的广泛应用,开发切实有效的极化滤波对抗方法已成为迫切需求.目前已经研究的滤波器按照设计思想可分为干扰抑制极化滤波器(Interference Suppression Polarization Filter,ISPF)[5，6]、信号匹配极化滤波器(SMPF)[8，9]和信干噪比优化极化滤波器[10].其中的干扰抑制极化滤波器,由于不仅具有快速自适应能力,且无需目标极化信息的先验知识,使其已成为工程应用中最为常用的极化滤波手段.对于该类滤波器干扰抑制性能的理论分析,能够指导实际工程中极化滤波器性能指标的制订及其适用性的评估.

极化度作为描述雷达电磁波部分极化特性的重要参数,因其具有较强的鲁棒性[11，12],且不受极化基改变的影响[13，14],从而被雷达极化技术研究者广泛关注.在极化滤波方面,文献[15]基于极化度参数对ISPF和SMPF(信号匹配极化滤波器)的性能进行了评估,并提出了对滤波器的选择建议.文献[16]则进一步分析了不同干噪比条件下,极化度对于ISPF性能的影响.因此极化度被认为是影响极化滤波器干扰抑制性能的主要因素,其被定义为电磁波中的完全极化波分量的功率与总功率的比值,然而揭示影响雷达接收电磁波极化度的物理成因鲜有报道.在雷达实际工作过程中,将不可避免的受到快速多变的电磁环境影响(例如多径效应以及大气传播效应等),雷达接收到的电磁波将不再是完全极化状态,因此用于表征其部分极化特性的极化度参数会相应地受到影响,而这种影响实际上将会直接导致滤波器性能的下降,单纯采用极化域滤波方法的干扰抑制能力会受到制约.

针对上述问题,一方面需要在考虑电磁环境扰动因素的基础上,建立对ISPF极化滤波器性能的评估模型,以便更为精确地阐述ISPF滤波方法的工程适用条件以及可达到的干扰抑制能力的上限;另一方面,在该影响不可避免的条件下,有必要寻找新的干扰抑制方法,以提高环境扰动条件下干扰抑制性能.本文首先分别在理想条件和环境扰动条件下建立了雷达双极化接收通道信号模型,利用极化相干矩阵给出了极化度的数学表达式,然后基于干扰抑制极化滤波器的设计思想,即干扰抑制最大化理论,推导并通过仿真分析了滤波器性能同干扰噪声功率比、环境扰动系数以及干扰信号极化状态之间的关系.在第3节中将环境扰动因素视为一种多源干扰的问题,建立了一种新的极化天线阵列构型,设计了主辅阵联合极化滤波(Main-auxiliary Array Joint Polarization Filter,MAJPF)方法.随后通过开展雷达外场抗干扰实验,利用实测数据进一步验证环境扰动因素对于极化滤波器的影响,同时对比了该因素影响下两种滤波器的干扰抑制性能,结果表明由于MAJPF方法结合了天线的极化域和空域特性,该滤波方法能够使滤波后信干噪比得到进一步改善.

2环境扰动建模

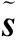
(1)

由于满足远场条件,式(1)可看作平面电磁波在一组正交基下的Jones矢量表征,根据电磁波极化理论,可以给出该接收电磁波的极化相干矩阵

(2)

式中E(·)用以表示集平均,将式(1)代入式(2),定义Ps=E(ss*),表示干扰信号功率.经整理后得到极化相干矩阵各元素可表示为

(3)

根据极化度同极化相干矩阵各元素间的关系[17],可以得到在不考虑环境扰动影响情况下雷达接收干扰信号极化度表达式

(4)

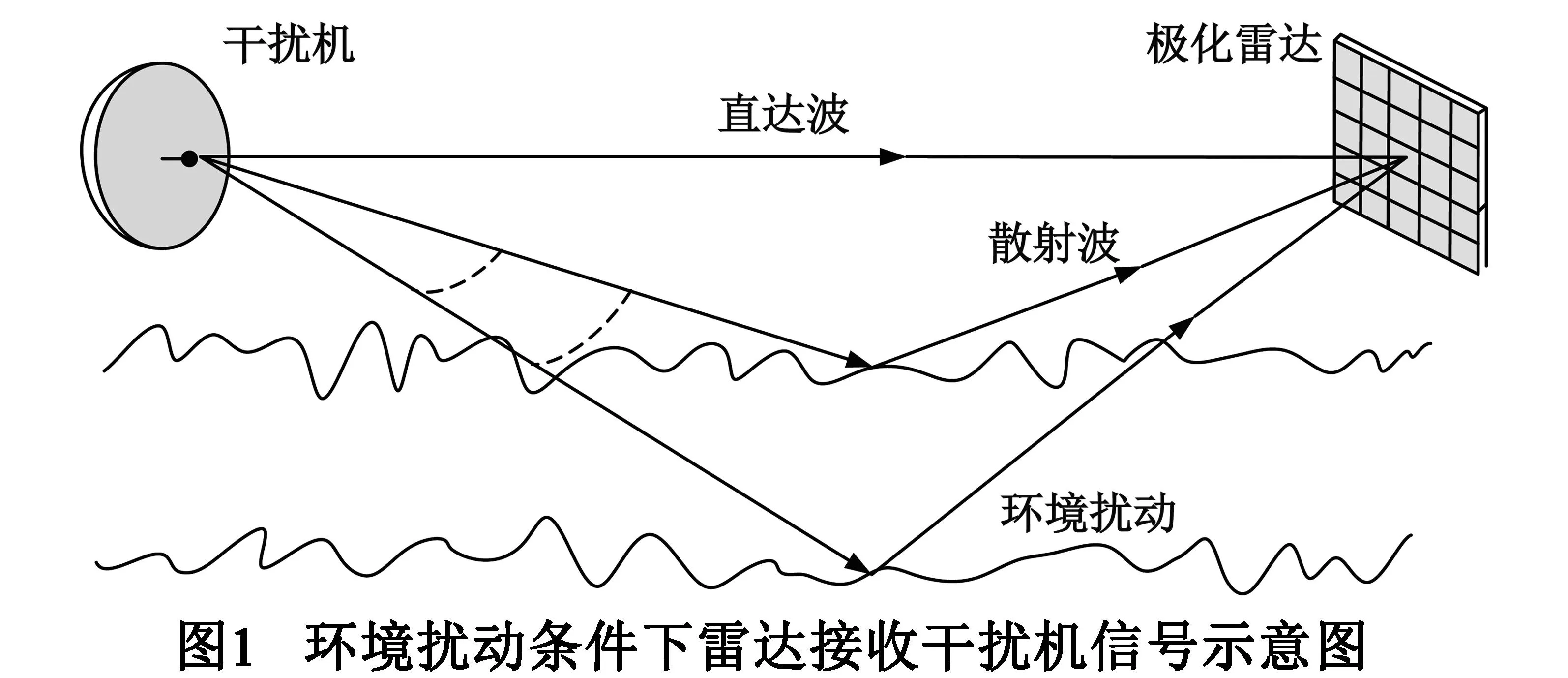
(5)

其中假设εH、εV、nH和nV之间相互独立,将上式代入式(2),得到环境扰动模型下接收电磁波的极化相干矩阵

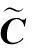
(6)

同样的根据相干矩阵可以得到该模型下的极化度.

(7)

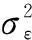
3基于环境扰动模型的ISPF抑制性能分析

上节中,我们基于理想条件和环境扰动条件建立了极化雷达接收信号模型,给出了影响电磁波极化度的环境扰动因素,为评估环境因素对于ISPF干扰抑制性能影响,下面分析极化度同此类滤波器的性能间的关系.我们假设天线的接收极化Jones矢量为h,经天线接收得到电磁波矢量x在天线端口产生开路电压为:

V=hTx

(8)

由式(8)可得到相应的接收信号功率为:

Pr=E(|V|2)=E((hTx)(hTx)H)

=hTE(xxH)h*=hTCh*

(9)

不难看式(9)为C的Hermite二次型,通过求取其最优值,可以得到ISPF通过接收变极化滤波所能达到的最佳性能.由于滤波的原理是依靠天线变极化引起接收功率的相对变化,并不关心天线的绝对增益值,因此进一步假设天线满足约束条件‖h‖=1,在该约束条件下根据Hermite二次型的性质,对任意的二维复矢量h,有如下关系:

λ1≤Pr=hTCh*≤λ2

(10)

其中λ1和λ2为矩阵C的两个特征值,且不妨假设λ1≤λ2,则利用矩阵特征值计算公式计算可得:

(11)

式中TrC=Cxx+Cyy,表示输入干扰的总功率(这里的干扰包括干扰机辐射的有源压制干扰直达波信号、电磁环境扰动引起的散射波信号以及通道热噪声等).PD表示干扰信号真实极化度在压制干扰条件下,为实现干扰抑制效果,需使接收到的干扰信号功率最小,则通过变极化能够得到的最小接收功率为:

(12)

我们定义接收机输入干扰总功率与输出功率比的最大值η作为判定变极化滤波器性能的上限指标,根据式(12)不难看出在干扰总功率一定的情况下,接收功率最小时干扰抑制比可达到最大,即

(13)

根据第2节的结果,分别将式(4)和式(7)代入式(13),得到描述理想情况下和存在环境扰动情况下的极化滤波器性能的解析表达式

η=

(14)

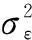
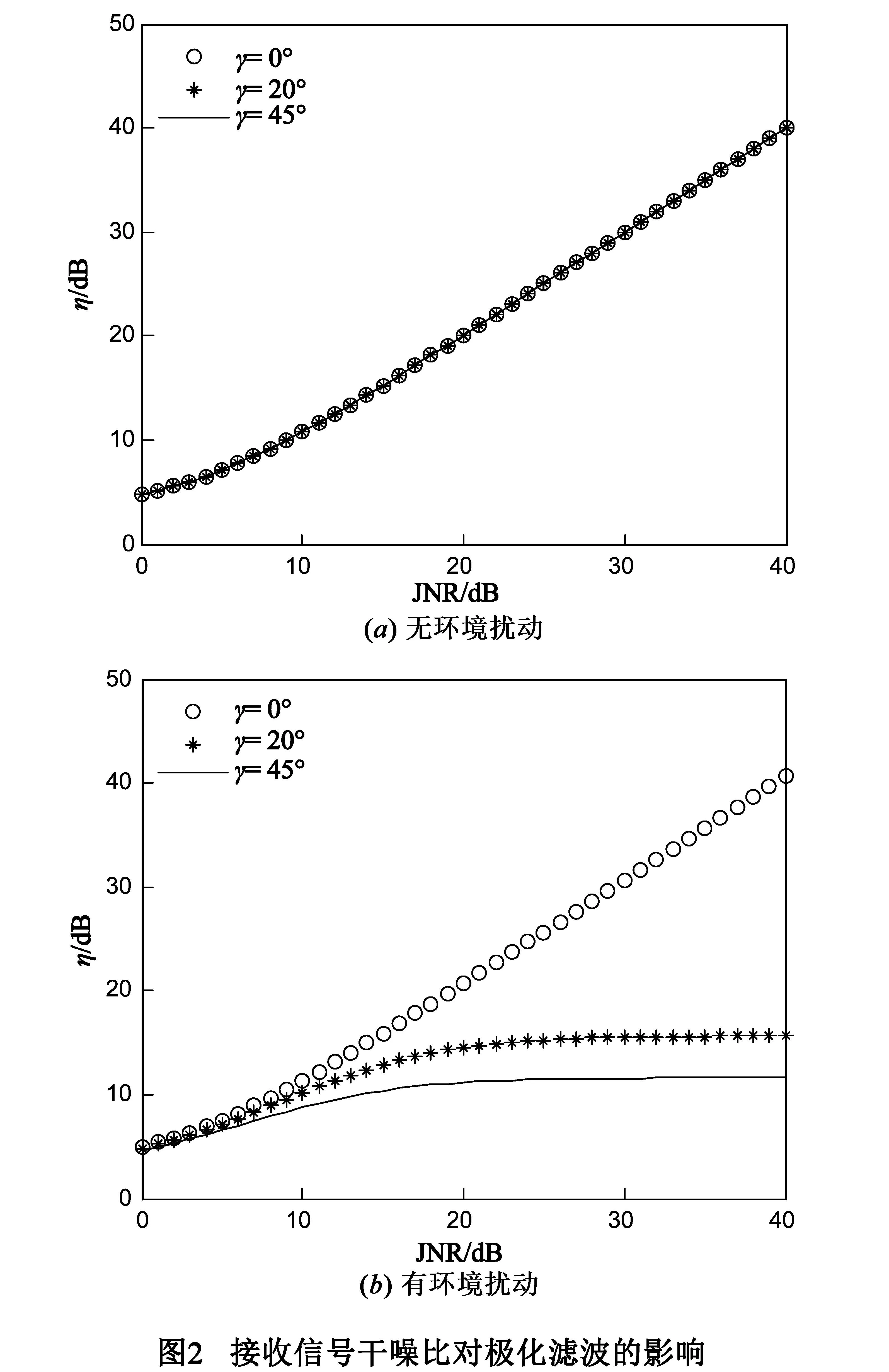
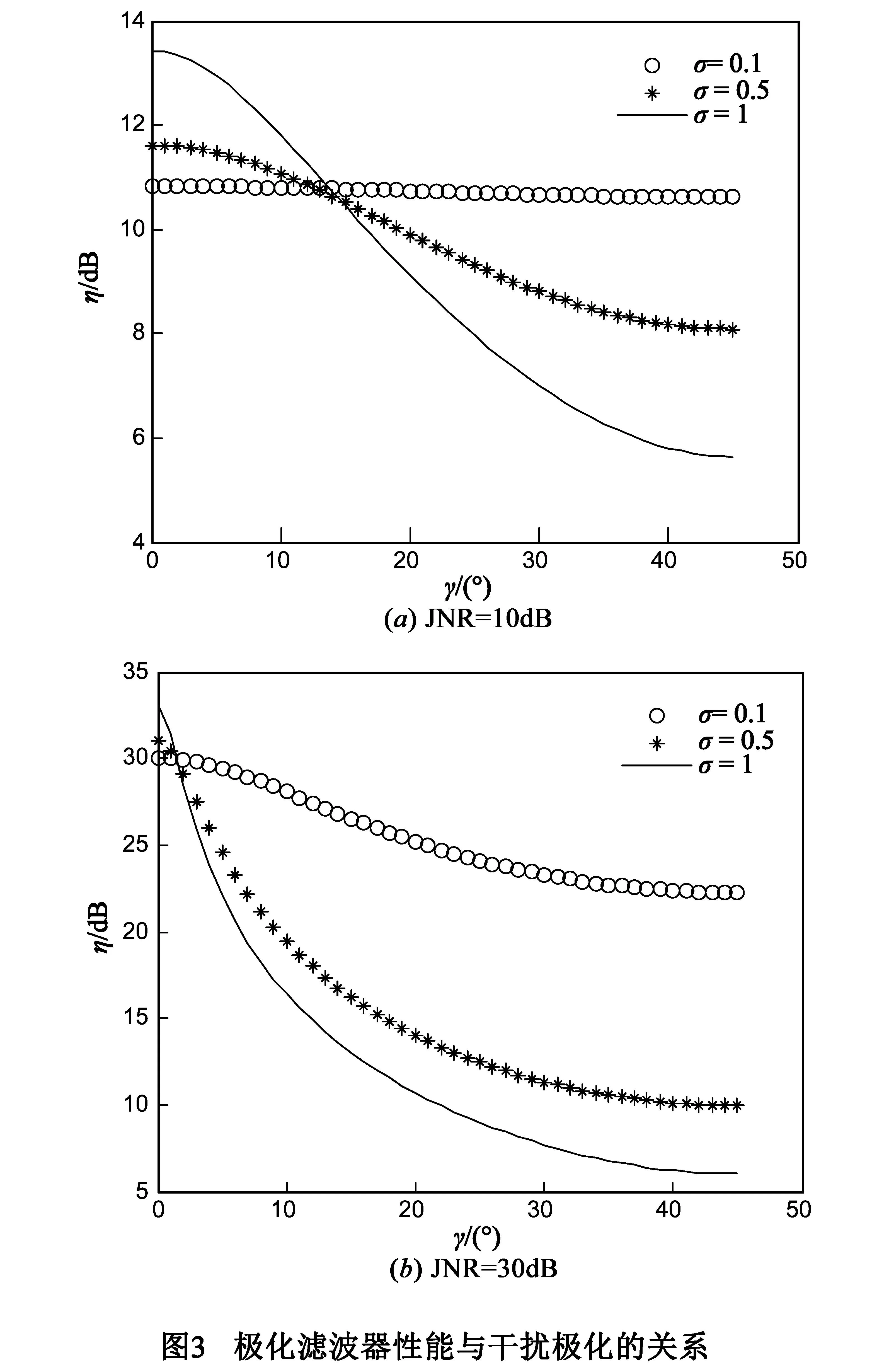
干扰极化状态在理想条件下不会影响滤波器性能,而当考虑环境扰动因素后,极化状态也成为制约滤波器性能的因素之一,仿真中分别固定干噪比为10dB和30dB,图3中选取了三种扰动系数,其标准差分别为0.1,0.5和1,观察仿真结果可得出如下结论:存在环境扰动因素情形下,干扰极化相位越接近45°,滤波器干扰抑制性能越差;扰动系数方差越大,滤波器性能受极化状态的影响越明显.对于较高干噪比情形,由于扰动因素对干扰信号的极化确定性破坏越严重,因此扰动系数越大使得滤波器干扰抑制比越小如图3(b),然而在低干噪比情形下,当干扰极化相位接近0°(或90°)时,如图3(a)所示,由于干扰信号几乎完全被某一极化通道接收,另一通道只存在热噪声,此时环境扰动因子在一定程度上提高了干扰噪声的功率比,其极化度相应得到提高,此时扰动系数越大干扰抑制比反而越高,即扰动因素在此情形下反而能够改善滤波器性能,然而一方面由于扰动因子受环境的影响,其方差一般不会很大,因此其改善量有限,由仿真结果可见最多只能提升2～3dB;另一方面对于大扰动因子而言,滤波器性能随角度变化衰减剧烈,其对于干扰极化的适应性变差.因此无论从滤波器干扰抑制性能或是滤波器适应干扰极化的稳定性来讲,环境扰动因素均会造成干扰抑制极化滤波器性能下降.

4主辅阵联合极化滤波方法

根据上节的分析可知单纯极化滤波方法受环境扰动因素影响严重,可以认为主要是由于类似多径的相干散射点的调制作用,使得接收到的合成信号的极化度降低.根据图1所示的场景,我们可以将该类环境扰动效应等效为干扰由多个方向进入雷达接收机的多源干扰问题.为了改善多源干扰影响下滤波器性能,除了利用主波束方向上的极化差异对抗干扰直达波外,还可以利用散射干扰源在空域上的差异,结合极化空域信息联合予以抑制.因此我们设计了一种带有辅助天线的极化阵列天线,其设计构型如图4所示,每个阵元由一组正交双极化偶极子构成,图中A代表所选取的辅助天线阵元,其余阵元构成主阵.假设主阵在(θ,φ)方向的天线增益为

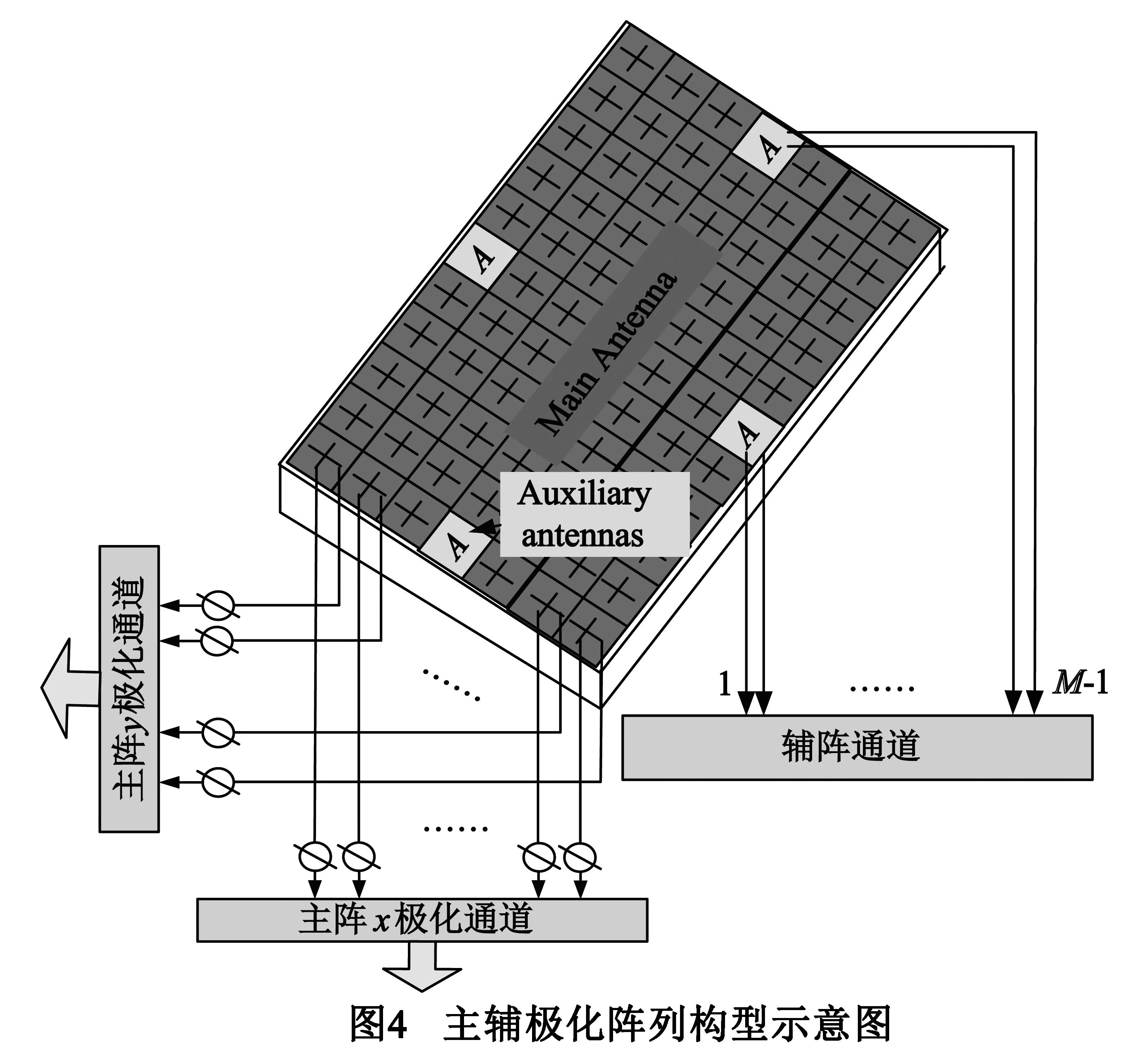
(15)

假设不考虑环境扰动时直达波干扰信号到达方向为(θ,φ),受波达方向的影响,每个阵元的正交极化天线接收到的电磁波极化矢量变为:

(16)

(γ,φ)在第2节中已经给出,为干扰信号极化相位描述子,则干扰到达天线前端的极化信号可表示为:

sP(t)=sP·s(t)

(17)

s(t)为包含干扰信号波形在内的信号复包络.结合该极化信号矢量可以给出图4所示的阵列天线各通道接收到的干扰信号的观测矢量为

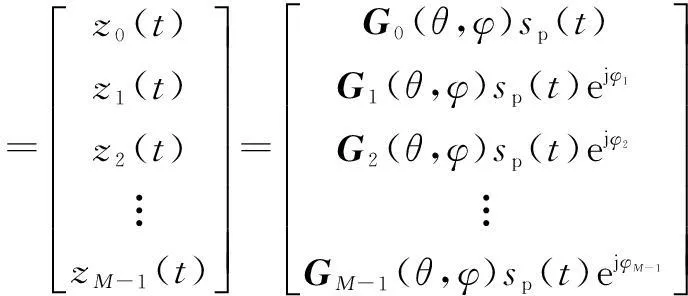
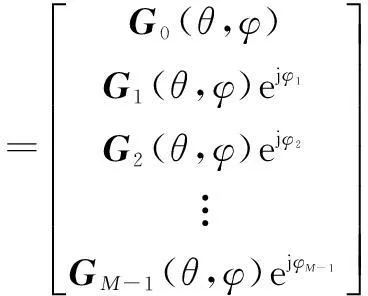
(18)

式中⊗代表Kronecker积,其中φi(i=1,…,M-1)为对应各辅助阵元通道相对主阵的接收信号相位滞后,将其中用于表示干扰极化域-空域的导向矢量简记为

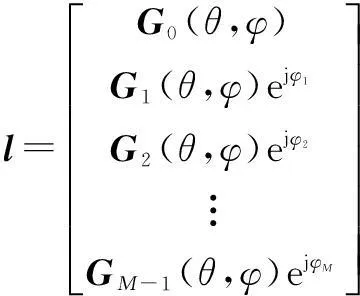
(19)

当我们考虑环境扰动因素时,可以看做多个辐射源信号的相干合成,此时假设通道内热噪声相互独立,则总的接收信号可表示为:

(20)

Y(t)=wHZ(t)

(21)

其中,加权矢量w∈C2M为2M维复矢量.

仍以干扰抑制最大化为优化目标,即按照输出干扰功率最小来求取最优加权系数.则该优化问题可等效为

(22)

令f(w)=wHRw,这里R=Z(t)Z(t)H,于是该优化问题是一种无约束的最优化问题,该优化问题的解向量可采用“最陡下降法”迭代计算[19],即

wn=wn-1-μw*f(w)

(23)

当权值收敛时即可得到最优的加权系数,代入公式(21)即可实现主辅阵联合极化滤波过程.该种滤波方法,在干扰信号受环境扰动因素影响而造成极化纯度降低的情形下,不仅利用了干扰信号的极化特征,也能结合干扰的空域特性,因此有望实现相比单纯极化滤波更好的干扰抑制效果,下面我们将通过开展极化雷达外场抗干扰实验进行分析和对比.

5外场实验结果与分析

首先,为了验证本文所建立的环境扰动模型,我们开展了双极化雷达对抗有源压制干扰的外场实验,实验场景及设备如图4所示,实验中利用干扰机(图4(b))对某双极化雷达实验系统释放具有确定极化的连续噪声式干扰信号,干扰极化状态为30°线极化,干扰机与雷达均置于水泥地面,相距约30m,摆放场景如图4(c)所示,雷达利用水平垂直正交双极化天线(图4(a))接收干扰信号,实验中各系统参数设定如表1所示,其中干扰机发射功率和天线增益可调.

表1　外场实验设备性能

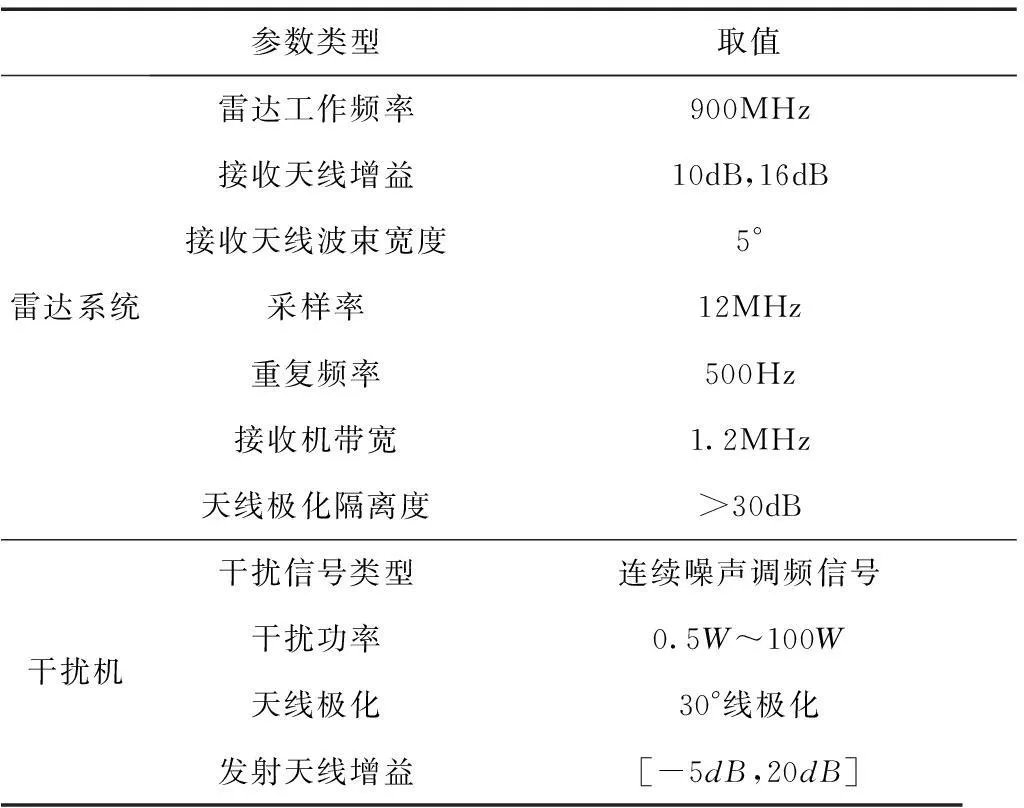
参数类型取值雷达系统雷达工作频率900MHz接收天线增益10dB,16dB接收天线波束宽度5°采样率12MHz重复频率500Hz接收机带宽1.2MHz天线极化隔离度>30dB干扰机干扰信号类型连续噪声调频信号干扰功率0.5W～100W天线极化30°线极化发射天线增益[-5dB,20dB]

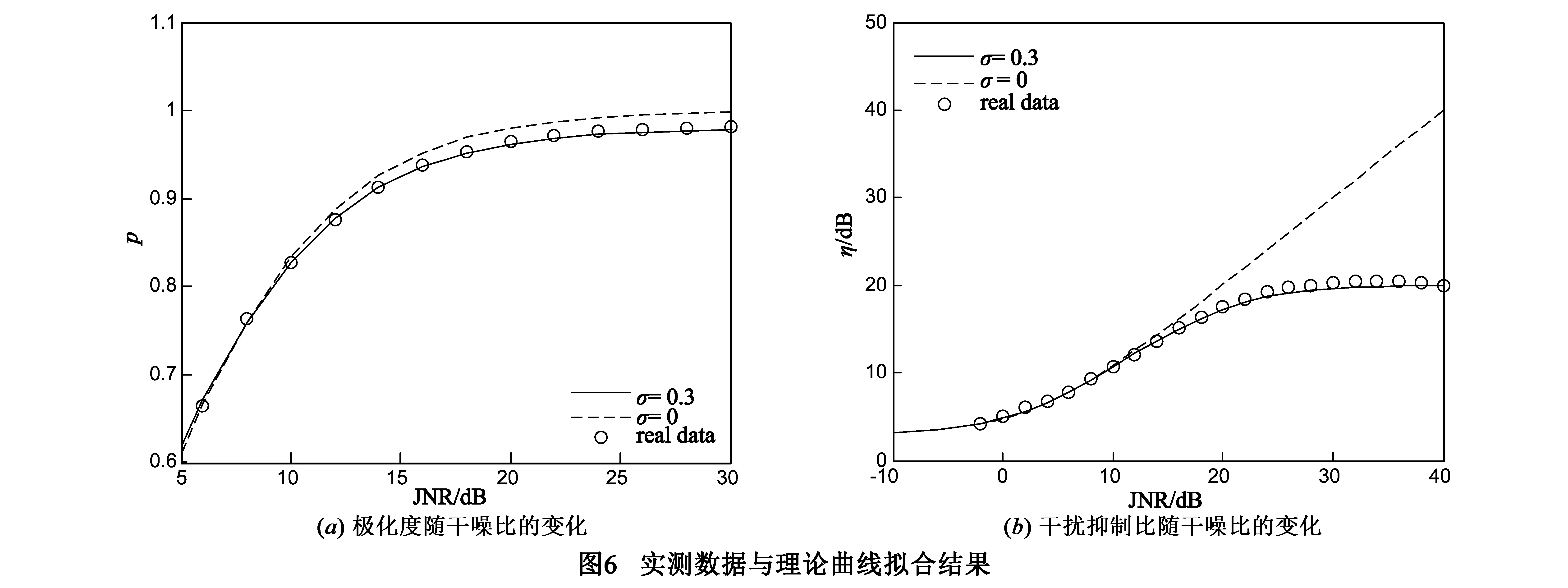
对接收到的信号进行采样,利用1000个重复周期的采样结果估计干扰信号的极化度,并利用ISPF对接收信号进行滤波处理,计算极化滤波前后干扰功率抑制比.为得到不同干噪比下的结果,以2dB为步长间隔改变干扰机发射增益,其余条件不变,重复上述信号采样、极化度估计和极化滤波处理过程,记录每次试验干噪比以及统计出的极化度和干扰抑制比的数值.图6即给出了极化度及干扰抑制比随干噪比变化的统计结果,同时利用本文给出的性能描述模型与试验结果比对.其中,图6(a)为采样数据的极化度估计值随干噪比变化与公式(7)所给的环境扰动模型的拟合结果,由图不难看出,实测数据明显已经背离了σε=0,即理想条件下的模型曲线,而与考虑环境扰动因素σε=0.3时的模型曲线拟合较好.对每一组干噪比下的试验结果作ISPF极化滤波处理,计算滤波前后的干扰抑制比,极化滤波器干扰抑制的性能曲线则被绘制在图6(b)中,同样的,受环境扰动因素的影响其滤波器性能偏离了理想条件下的理论模型,而与扰动模型下的抑制比曲线匹配更好.从而足以证明确实存在环境扰动分量制约极化滤波器的抗干扰能力.

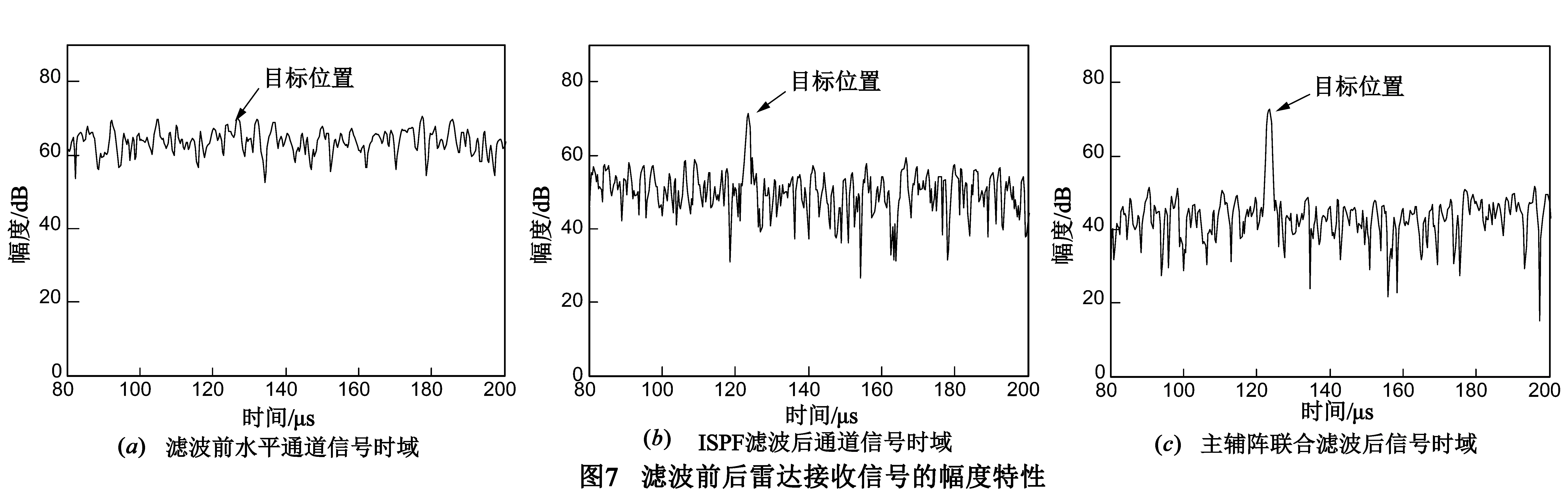
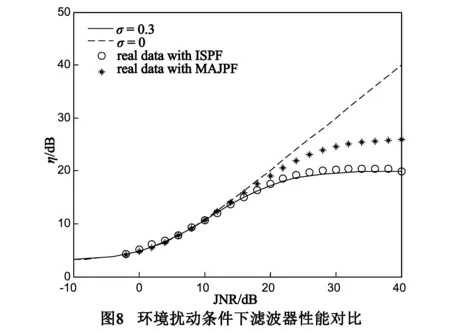
接着,考虑本文提出的MAJPF方法在环境扰动影响下对干扰抑制性能的改善.为实现该滤波方法,我们选取了接收阵列天线中的1号、8号、9号和16号阵元作为辅助天线,其余阵元构成主通道,如图4(a)所示.此外,增加一水平极化信号源发射线性调频脉冲信号用以模拟目标回波,调整信号源发射功率使得无干扰情形下雷达接收信噪比约13dB.设定干噪比为26dB,根据第4节给出的方法构建主辅通道接收矢量样本,在对每个通道做脉冲压缩处理后,借鉴文献中的方法选取干扰样本,采用最陡梯度迭代方法计算各通道最优加权系数,并做加权处理,环境扰动条件下两种滤波器滤波前后的幅度特性由由图7给出,图7(a)为滤波处理前水平通道的幅度特性,目标信号此时已被干扰“淹没”,图7(b)和图7(c)则分别为ISPF和MAJPF滤波处理后的信号时域包络,不难发现两种滤波方法都能够有效抑制干扰,目标信号被显露出来,经ISPF处理后SIR为8.54dB,而经主辅阵联合处理后SIR可达12.35dB,相比而言后者所抑制的干扰功率更多,信干噪比改善更为明显.最后,统计并对比每组干噪比样本分别经ISPF和MAJPF滤波器处理后干扰抑制性能,如图8所示,图中星号即代表MAJPF滤波器干扰抑制性能.对比不难看出,当干噪比较低时(JNR<12dB),两种滤波方法干扰抑制性能相近,但随着干噪比的增大,环境扰动因素对ISPF滤波器的性能影响更为严重,而对MAJPF方法的影响较小,这主要是由于ISPF方法仅从极化域处理,而当环境扰动因素破坏了干扰的极化纯度后,滤波性能将受到限制;新的MAJPF滤波方法结合了干扰的空域和极化域特性,能够在高自由度的建立干扰子空间,从而对环境扰动因素所造成的影响具有更好的兼容性,干扰抑制性能也更为优越.

6结论

本文中我们研究了环境扰动因素影响下极化雷达对噪声干扰信号的接收和抑制问题,建立了干扰抑制极化滤波器性能同干噪比,干扰极化状态以及扰动系数的关系模型.通过实验发现受环境扰动因素的影响,干扰极化相位越接近45°滤波器性能越差,且滤波所能得到的干扰抑制比会被限制在某一上限,而不会随干噪比增大而成线性增长关系.这一结论有助于极化滤波器在工程中确立更精准的性能指标.

为改善环境扰动条件下干扰抑制性能,我们设计了一种新的主辅极化阵列天线构型,在此基础上给出了基于主辅阵通道的联合极化滤波方法.最后通过外场的干扰对抗实验,一方面验证了环境扰动因素对于极化滤波器性能的制约作用,理论模型与实验结果的良好拟合说明了本文所提扰动模型在实际工程中用于描述滤波器性能方面的适用性;另一方面通过对比ISPF和MAJPF滤波器性能说明了新的干扰抑制方法能够在环境扰动因素存在的条件下有效提升信干噪比.本文的研究结论能够为极化滤波器的实际应用提供相应的理论支撑,扰动模型对极化雷达检测理论的扩展将作为后续开展的研究内容.

参考文献

[1]GIULI D.Polarization diversity in radars[J].Proceedings of the IEEE,1986,72(2):245-267.

[2]STAPOR D P.Optimal receive antenna polaization in the presence of interference and noise[J].IEEE Trans on Antennas and Propagation,1995,43(5):473-477.

[3]DAI H Y,WANG X S,LI Y Z,et al.Main-lobe jamming suppression method of using spatial polarization characteristics of antennas[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(3):2167-2179.

[4]任博,等.抑制雷达主波束内GSM干扰的极化滤波方法研究[J].电子与信息学报,2014,33(2):290-295.

REN B,et al.Investigation on of polarization filtering scheme to suppress GSM interference in radar main beam[J].Journal of Electronics & Information Technology,2014,33(2):290-295.(in Chinese)

[5]施龙飞,等.APC迭代滤波算法与性能分析[J].电子与信息学报,2006,28(9):1560-1564.

Shi L F,et al.The iterative-filtering scheme and its performance analysis of APC[J].Journal of Electronics & Information Technology,2006,28(9):1560-1564.(in Chinese)

[6]POELMAN A J,et al.Multinotch logic-product polarization suppression filters:A typical design example and its performance in a rain clutter environment[J].IEE Proceedings of Communications,Radar and Signal Processing,1984,131(7):383-396.

[7]任博,等.应用极化聚类中心设计快速自适应极化滤波器[J].国防科技大学学报,2015,37(4):87-92.

REN B,et al.Design of fast adaptive polarization filters utilizing polarizing cluster center[J].Journal of National University of Defense Technology,2015,37(4):87-92.(in Chinese)

[8]DAI H Y,WANG X S,LI Y Z,et al.Main-lobe jamming suppression method of using spatial polarization characteristics of antennas[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(3):2167-2179.

[9]MAO X P,et al.Oblique projection polarisation filtering for interference suppression in high-frequency surface wave radar[J].IET Radar Sonar & Navigation,2012,6(2):71-80.

[10]WANG X S,CHANG Y L,DAI D H,et al.Band characteristics of SINR polarization filter[J].IEEE Transactions on Antennas Propagation,2007,55(4):1148-1154.

[11]GALLETI M,ZRNIC D S.Degree of polarization at simultaneous transmit:theoretical aspects[J].IEEE Geoscience and Remote Sensing Letters,2012,9(3):383-387.

[12]GALLETI M,ZRNIC D S,MELNIKOV V M,et al.Degree of polarization at horizontal transmit theory and applications for weather radar[J].IEEE Transactions on Geoscience and Remote Sensing,2012,50(4):1291-1301.

[13]RIO V S D,MOSQUERA J M P,ISASA M V,et al.Statistics of the degree of polarization[J].IEEE Transactions on Antennas and Propagation,2006,54(7):2173-2175.

[14]GALLETI M,et al.Zenith nadir pointing mm-wave radars linear or circular polarization[J].IEEE Transactions on Geoscience and Remote Sensing,2014,52(1):628-638.

[15]王雪松,代大海,徐振海,等.极化滤波器的性能评估与选择[J].自然科学进展,2004,(04):84-90.

WANG X S,DAI D H,XU Z H,et al.Performance evaluation and selection of the polarization filters[J].Progress in Natural Science,2004,(04):84-90.(in Chinese)

[16]王雪松,等.自适应极化滤波器的理论性能分析[J].电子学报,2004,32(4):1326-1329.

WANG X S,et al.Theoretical performance analysis of adaptive polarization filters[J].Acta Electronica Sinica,2004,32(4):1326-1329.(in Chinese)

[17]WOLF E.Coherence properties of partially polarized electromagnetic radiation[J].Ⅱ Nuovo Cimento,1959,XIII(6):1165-1181.

[18]HOIJER M.Polarization of the electromagnetic field radiated from a random emitter and its coupling to a general antenna[J].IEEE Transactions on Electromagnetic Compatibility,2013,55(6):1335-1337.

[19]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

任博(通信作者)男,1986年2月出生于河北省邯郸市,2009年获得北京航空航天大学工学学士学位,2011年获得国防科技大学电子科学与工程学院硕士学位,现为该院博士研究生,研究方向为雷达极化信息处理,综合电子信息系统建模与仿真.

E-mail:rb410@139.com

施龙飞男,1978年出生,博士,电子信息系统复杂电磁环境效应(CEMEE)国家重点实验室副研究员,主要研究方向为雷达极化抗干扰,雷达对抗技术.

E-mail:longfei-shi@sina.com

Study on the Performance of Interference Suppression Polarization Filter Based on Environment Disturbance Model

REN Bo1,2,SHI Long-fei1,2,WANG Guo-yu1,2

(1.StateKeyLaboratoryofComplexElectromagneticEnvironmentEffectsonElectronics&InformationSystem,NationalUniversityofDefenseTechnology,Hunan,Changsha410073,China;2.CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Hunan,Changsha410073,China)

Abstract:The interference signal in radar main-beam can be suppressed by polarization filter,if the radar has ability of dual-polarization receiving.However,the polarization character of the interference can be disturbed by the real propagation environment like multipath effect.The degree of polarization from the real reception signals can be influenced,as well as the interference suppression performance of the polarization filter.Based on the requirement of the performance analysis of interference suppression polarization filter (ISPF),the math model used to describe the performance of the ISPF is established both in the ideal situation and in the environmental disturbance situation.Combined with the simulation,the performance of ISPF is analyzed with the relationship of interference-noise rate,polarization state of interference and environment coefficient.In order to improve the performance of interference suppression in the environmental disturbance situation,a novel scheme of the main-auxiliary array joint polarization filter (MAJPF) is proposed.Ultimately,the anti-interference experiment is developed to demonstrate the influence of the environment disturbance on the ISPF.Meanwhile,the performances of the two filters are compared based on the environmental disturbance situation.The comparison results show the interference suppression advantage of the novel filter scheme against the disturbance situation.

Key words:polarization filter;degree of polarization;environment disturbance model

作者简介

DOI:电子学报URL:http://www.ejournal.org.cn10.3969/j.issn.0372-2112.2016.03.005

中图分类号:TN957.51

文献标识码：A

文章编号：0372-2112 (2016)03-0527-08

基金项目:国家自然科学基金(No.61490692)

收稿日期:2014-06-19;修回日期:2015-12-28;责任编辑:马兰英