无需光速不变假设的狭义相对论新推导

戴又善， 宋孝同

(1.浙江大学城市学院， 浙江 杭州 310015； 2.浙江大学 物理系， 浙江 杭州 310027；3.弗吉尼亚大学 粒子与核物理研究所，弗吉尼亚州 夏洛茨维尔 22904)



无需光速不变假设的狭义相对论新推导

戴又善1， 宋孝同2,3

(1.浙江大学城市学院， 浙江 杭州 310015； 2.浙江大学 物理系， 浙江 杭州 310027；3.弗吉尼亚大学 粒子与核物理研究所，弗吉尼亚州 夏洛茨维尔 22904)

摘要：传统相对论依据光速不变原理可以推导出时空的洛伦兹变换公式，而在相对性原理的基础上，利用洛伦兹变换公式和守恒定律又可建立起爱因斯坦的质能关系式.不同于首先从运动学出发来完全确定洛伦兹变换的传统方法,依据相对性原理以及动量和能量守恒,通过讨论粒子的两体衰变过程,论证了相对论能量正比于动质量实际上并不依赖于洛伦兹变换或具体的时空变换特性.从而无须引进光速不变假设和不依赖静质量为0的粒子,给出了一种更为普遍的狭义相对论的新推导.新的相对论公式已不再需要依赖光速,取而代之的是与所有粒子相关的普适极限速度vm.

关键词：狭义相对论; 相对论动力学; 光速不变原理; 质速关系; 质能关系

DAI Youshan1, SONG Xiaotong2,3

(1.ZhejiangUniversityCityCollege,Hangzhou310015,China; 2.DepartmentofPhysics,ZhejiangUniversity,Hangzhou310027,China; 3.InstituteofNuclearandParticlePhysics,UniversityofVirginia,CharlottesvilleVA22904,USA)

爱因斯坦于1905年依据相对性原理和光速不变原理,创建了狭义相对论[1-2](以下简称相对论).100多年来,尽管相对论经受了大量实验的检验,取得了巨大的成功,但是将相对论这一普遍适用的基础理论建立在特殊物质光的特性之上，存在明显的理论局限性.虽然也有研究提出可以用物质运动速度存在上限的假设来替代光速不变的假设[3-4],以避免将普遍的相对论理论建立在具体的物质特性之上,但这一假设实际上隐含了自然界必须存在以速度上限值运动的粒子的假定[5],即传统相对论理论的建立必须依赖于某种以极限速度运动即静质量为0的粒子(例如光子).

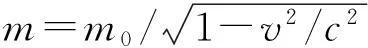
不同于依据光速不变假设首先从运动学来完全确定洛伦兹变换的传统方法,本文将从动力学过程出发来建立相对论.首先，依据相对性原理以及动量和能量守恒定律,通过讨论粒子的两体衰变过程,论证相对论能量正比于动质量实际上并不依赖于洛伦兹变换或具体的时空变换特性,对一般的线性时空变换都有E=mA,其中A为与粒子运动速度无关的待定常量[10-11].在此关键性证明的基础上,本文针对静质量不为0的粒子,无须引进光速不变假设,仅仅依据相对性原理就可建立起相对论动力学,进一步可以完全确定线性时空变换的广义洛伦兹变换公式,从而给出了一种适用范围更广的相对论理论的新推导.新的相对论公式已不再与光速c直接相关,取而代之的是在建立和求解粒子质速关系的微分方程时自动给出与所有粒子相关的普适极限速度vm.

1质速关系和质能关系的推导

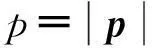
p=m0γ(v2)v=mv.

(1)

上式中m可称为动质量,而m=m0γ(v2)通常称为质速关系.对于m0>0粒子的能量E=E(m0,v),同样可写为

E=m0Γ(v2),

(2)

其中Γ(v2)为另一待定函数.

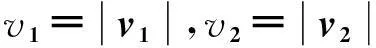
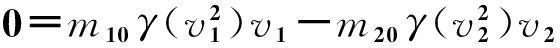
(3)

由能量守恒可得

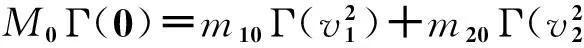
(4)

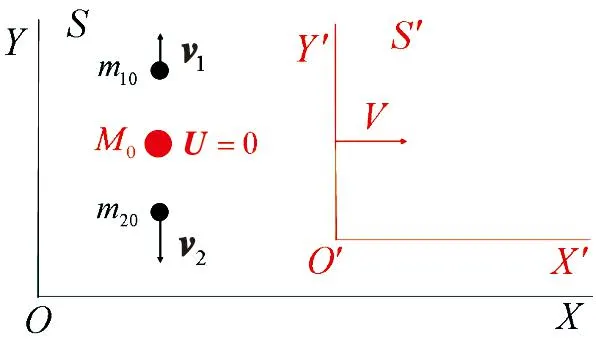
图1　M0粒子两体衰变过程的不同惯性系变换Fig.1　Two-body decay process of particle M0for inertial frames transformation

设S′系相对于S系沿X方向以速度V运动(见图1).一般的线性时空变换关系为

(5)

(6)

对上式微分,即可求得一般的速度变换关系为

(7)

目前a01(V)和a00(V)还是未知的待定系数,因而时空变换关系和速度变换关系还未完全确定[10-11].

即有

(8)

依据相对性原理在S′系中应同样满足动量守恒和能量守恒：

(9)

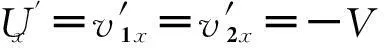
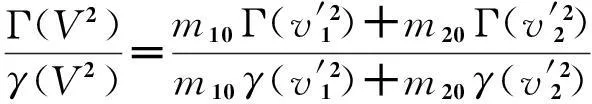
(10)

令

(11)

由式(10)可得

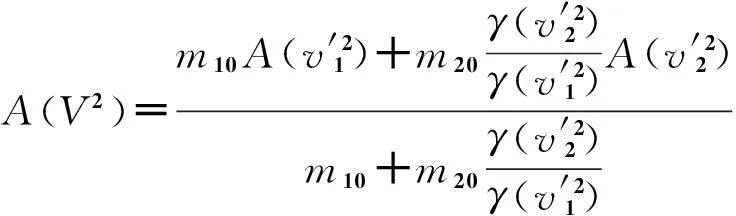
(12)

A(V2)=A(v′21)=A(v′22).

(13)

虽然上式是在m10=m20的特例下推得,但显然在m10≠m20的一般情况下,式(13)也是方程式(12)的解.由于在速度允许取值范围内,V和v1(或V和v2)都为独立参量,因而由式(8)可知V2和v′21(或V2和v′22)均可独立地变化,因此在速度允许的取值范围内A(v2)必须是与粒子运动速度无关的常量,由此可知

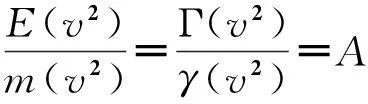
(14)

即粒子能量和动质量之比是与参考系选取无关的待定常量,由此证明了粒子相对论能量应正比于动质量而并不依赖于具体的线性时空变换形式.因此粒子能量E(v2)和静能E0=E(0)可以分别写为

E(v2)=m(v2)A,E0=m0A.

(15)

设粒子所受外力为F,在相对论力学中粒子的动量和能量的变化分别为dp=Fdt，dE=F·dr，由此可得能量变化和动量变化之间的关系:

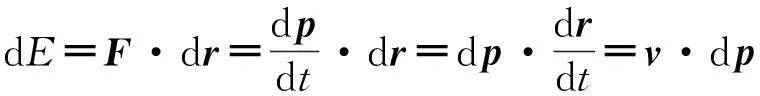
(16)

则有

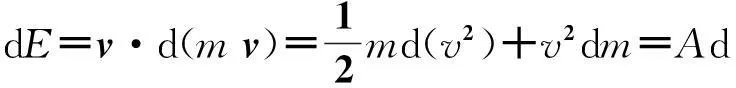
(17)

由此可建立微分方程

(18)

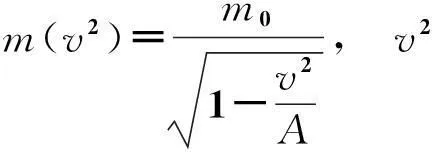
(19)

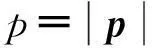
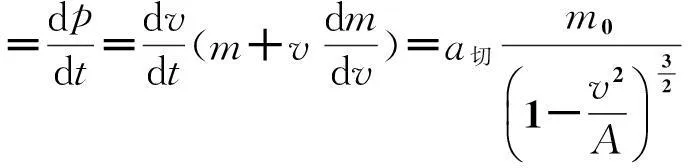
(20)

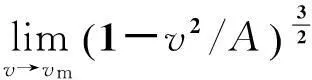
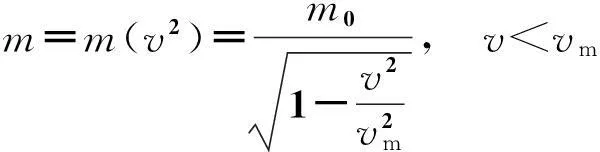
(21)

而粒子的质能关系则为

(22)

2广义洛伦兹变换公式的推导

利用已确定的质速关系和质能关系,代入S系的能量守恒关系式(4)得

(23)

代入S′系的能量守恒关系式(9)则可得

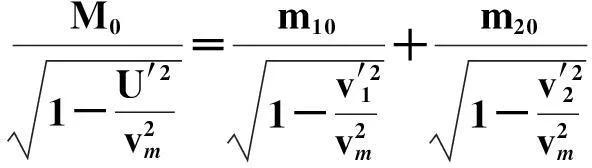
(24)

将S′系的粒子速度式(8)代入式(24)即有

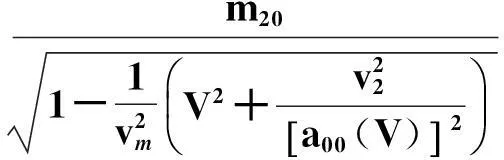
(25)

比较式(25)与(23)则有

(26)

由此可求得(要求满足a00(V=0)=1)

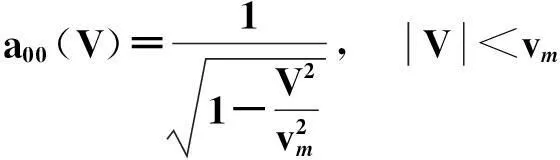
(27)

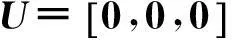
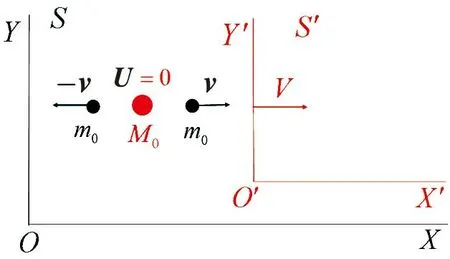
图2　不同惯性系中M0粒子的相等静质量两体衰变Fig.2　Two-body decay process of particle M0with same rest mass in different inertial frames

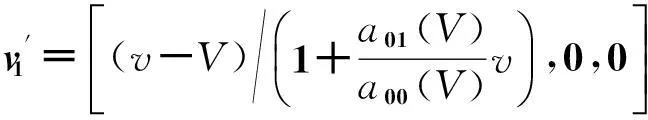
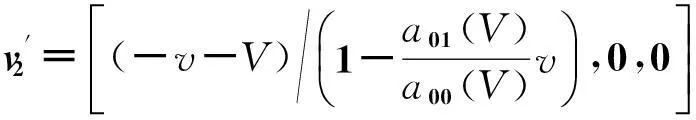
即有

(28)

由S′系X方向的动量守恒以及能量守恒可得

(29)

即有

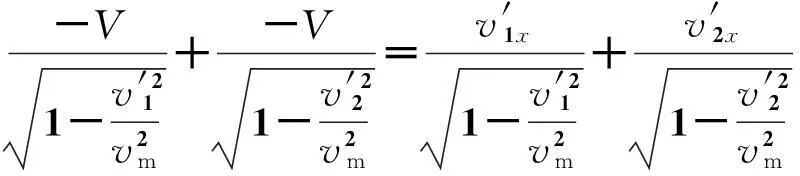
(30)

由此可得

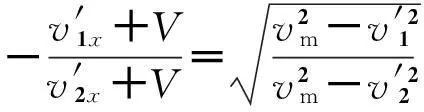
(31)

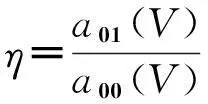
(32)

代入式(31)后可得

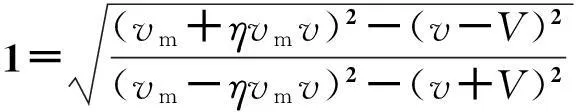
(33)

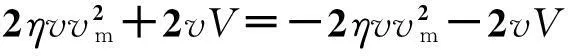
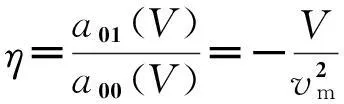
(34)

由式(27)可得

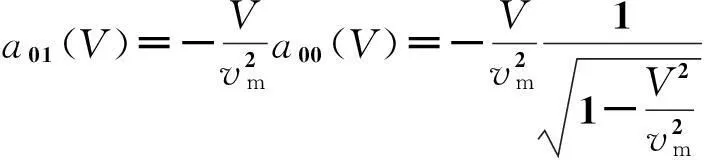
(35)

需要说明的是,一般线性时空变换的a01(V)和a00(V)并不独立,由相对论运动学可知两者必须满足关系[12]:

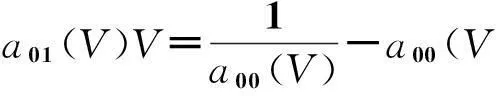
(36)

而上述推导则用动力学过程再次证明了这一关系式.

确定了具体的a01(V)和a00(V)后,代入式(6)就可得到相对论的时空变换关系：

(37)

可将上式称为广义洛伦兹变换,其中vm代表了更具普遍性的粒子运动极限速度.若取极限速度为光速vm=c,即式(37)为传统相对论的洛伦兹变换;若取vm→∞,则回到了经典绝对时空观的伽利略变换.

依据式(7)则可确定相对论的速度变换关系为

(38)

由式(38)可直接验证极限速度vm为广义洛伦兹变换下的不变量，并可证明vm是对所有m0≠0粒子都适用的普适常量[11-12].若取vm=c,则光速不变就成了相对论的一个推论.

3结论

以上基于相对性原理以及动力学的基本关系dE=v·dp,通过讨论静质量不为0粒子的两体衰变过程,依据动量守恒和能量守恒定律，首先推导了相对论的质速关系和质能关系.由于在推导中无须事先确定运动学的时空变换和速度变换公式,因而相对论质速关系和质能关系在本质上并不依赖于运动学具体的时空变换特性,完全可由相对论动力学所确定[10-12].在此基础上可进一步完全确定相对论运动学的广义洛伦兹变换公式,从而建立了相比于传统相对论适用范围更广的相对论理论新框架.

需要指出的是,通过一般运动学的讨论可以证明,对于m0>0的具有静止参考系的粒子,伽利略变换是唯一允许粒子运动速度为任意大的线性时空变换,因而对于任何非伽利略型线性时空变换,必然要求粒子的运动速度存在上限[12].而本文则由动力学过程通过建立和求解粒子质速关系的微分方程,再次证明了对于m0>0粒子的运动速度必须存在上限.本文的推导说明,从动力学角度出发来讨论相对论,依据相对性原理将自动导致m0>0粒子的运动速度具有上限,而无须通过额外的理论假设来引入极限速度,因而无须引进光速不变的假设就可以给出广义洛伦兹变换的推导.

值得强调的是,在传统相对论的建立过程中,必须事先在运动学中依赖以极限速度运动即静质量为0的粒子,才能推导出洛伦兹变换公式.而在本文的动力学过程推导中则完全与静质量为0的粒子无关,也不再需要光速不变的假设.本文的研究结果说明相对论是一个并不依赖于任何特殊粒子具体特性而适用于所有物质的普遍理论,即使自然界存在超光速现象，其与相对论理论也是可以相容的[13].在新的相对论公式中,由普适极限速度vm取代了光速c,而vm的具体取值可通过实验测量来确定.由于以极限速度vm运动的粒子不存在静止参考系,则静质量不为0的粒子只能趋近极限速度而无法达到极限速度,因而粒子以极限速度运动等价于该粒子的静质量严格为0,即vm=c等价于光子的m0=0.但由于目前实验上还未能确定光子的静质量是否严格为0,因此极限速度是否严格等于光速也还未能确定.若vm≠c,则光速不变将不再成立;若vm=c(严格相等),则光速不变就成为相对论的一个推论而不再是原理假设.因而无论自然界是否存在静质量为0的粒子,无论极限速度是否等于光速,也无论今后是否发现超光速现象,相对论都是成立与自洽的[14-16].由于本文证明了相对论的建立无须引进光速不变假设且不依赖静质量为0的粒子,本文的研究结果将使得相对论的理论基础更加稳固,其应用范围也更为广泛.

参考文献(References)：

[1]EINSTEIN A. Zur elektro-dynamik bewegter körper[J]. Annalen der Physik,1905, 17: 891-921.

[2]EINSTEIN A. Ist die trägheit eines körpers von seinem energieinhalt abhänging?[J]. Annalen der Physik,1905, 18: 639-641.

[3]LANDAU L D, LIFSHITZ E M. The Classical Theory of Fields[M].3rd ed， Oxford: Elsevier Science Ltd, 1976.

[4]MERMIN N D. Relativity without light[J]. Am J Phys,1984, 52: 119-124.

[5]JACKSON J D. Classical Electrodynamics[M]. 3rd ed， New York: John Wiley & Sons, 1998.

[6]EINSTEIN A. An elementary derivation of the equivalence of mass and energy[J]. Technical Journal,1946(5): 16-17.

[7]EINSTEIN A.E=mc2, the most urgent problem[J]. Science Illustrated,1946(1): 16-17.

[8]SCHWARTZ H M. Introduction to Special Relativity[M]. New York: McGraw-Hill, 1968.

[9]SARD R D. Relativistic Mechanics[M]. New York: Benjamin, 1970.

[10]戴又善.无需利用洛伦兹变换的相对论质能关系新推导[J].大学物理,2013,32(2):37-39.

DAI Youshan. Derivation of the mass-energy relation dispense with Lorentz transformation[J]. College Physics,2013,32(2):37-39.

[11]戴又善,戴亮.普遍的质速关系和狭义相对论[J].北京大学学报:自然科学版,2014,50(3):403-410.

DAI Youshan, DAI Liang. Universal mass-velocity relation and special relativity[J]. Acta Scientiarum Naturalium Universitatis Pekinensis,2014,50(3):403-410.

[12]戴又善.狭义相对论与运动速度上限[J].北京大学学报:自然科学版,2013,49(3):356-364.

DAI Youshan. Special relativity and upper limit for speed[J]. Acta Scientiarum Naturalium Universitatis Pekinensis,2013, 49(3): 356-364.

[13]LIBERATI S, SONEGO S, VISSER M. Faster-than-csignals, special relativity, and causality[J]. Annals of Physics,2002, 298: 167-185.

[14]OPEAR C, ADAM T, AGAFONOVA N, et al. Measurement of the neutrino velocity with the OPERA detect in the CNGS beam[J]. Journal of High Energy Physics,2012, 1210: 93.

[15]COHEN A G, GLASHOW S L. New constraints on neutrino velocities[J]. Phys Rev Lett,2011, 107，doi:http://dxdoi.org/10.1103/PhysRevLett.107.181803.

[16]BACCETTI V, TAKE K, VISSER M. Lorentz velocities kinematics: Threshold theorems[J]. Journal of High Energy Physics,2012(3): 1-28.

New derivation of special relativity without assumption of constant speed of light. Journal of Zhejiang University(Science Edition), 2016,43(2):247-252

Abstract:Traditionally, special relativity is formulated through a derivation of the space-time Lorentz transformation based on the assumption that the speed of light is invariant. Einstein’s famous mass-energy relation can be deduced from the Lorentz transformation, combined with the principle of relativity as well as the relevant conservation laws. This work abandons the unnecessary assumption of a constant speed of light, and proves that the proportionality between the relativistic energy and the moving mass does not rely on Lorentz transformation or any other specific form of space-time transformation. We demonstrate with two-body particle decay following directly from the principle of relativity and the conservation of energy and momentum. Therefore, we present a novel and more general formulation of special relativity without assuming a constant speed of light and the existence of massless particles. In this new formulation, a universal speed limit vm naturally emerges with no specific regard to the propagation of light.

Key Words:special relativity; relativistic dynamics; principle of constant speed of light; mass-velocity relation; mass-energy relation

中图分类号：O 412.1

文献标志码：A

文章编号：1008-9497(2016)02-247-06

DOI:10.3785/j.issn.1008-9497.2016.02.022

作者简介：戴又善(1957-)，ORCID:http://orcid.org/0000-0003-2318-2196,男，博士，副教授，主要从事理论物理研究，E-mail:daiys@zucc.edu.cn.

收稿日期：2014-12-01.