基于模拟退火遗传算法的三值FPRM电路功耗优化

厉康平，汪鹏君，张会红

(宁波大学 电路与系统研究所, 浙江 宁波 315211)



基于模拟退火遗传算法的三值FPRM电路功耗优化

厉康平，汪鹏君*，张会红

(宁波大学 电路与系统研究所, 浙江 宁波 315211)

摘要：在三值FPRM(Fixed-Polarity Reed-Muller)逻辑函数中,n变量函数有3n个固定极性.针对不同极性下FPRM电路功耗不同的特点，研究了三值FPRM逻辑表达式,提出一种基于模拟退火遗传算法的三值FPRM电路功耗优化方法.首先,根据三值逻辑函数表达式和开关信号传递理论,建立三值FPRM电路功耗估计模型;再利用模拟退火遗传算法对三值FPRM电路进行功耗最佳极性搜索,得到了功耗最低的FPRM电路;最后对13个MCNC Benchmark电路进行仿真.结果表明:与0极性相比,搜索到的最佳极性功耗平均节省了73.98%.

关键词：三值逻辑函数; FPRM电路; 模拟退火遗传算法; 功耗

LI Kangping, WANG Pengjun, ZHANG Huihong.

(InstituteofCircuitsandSystems,NingboUniversity,Ningbo315211,ZhejiangProvince,China)

随着集成电路规模的扩大，集成度不断提高,数字电路的功耗与面积等问题尤显突出[1].传统的数字电路大都采用二值逻辑,但其信息含量低已成为制约集成电路发展的主要因素.多值逻辑电路增加了单线携带信息的能力,能有效提高空间或时间的利用率,减少数字系统的连线,节省电路面积与成本[2].其中，基数为3的三值逻辑因其基数最小,而较易实现,具有代表性.

任意三值逻辑函数均可用布尔逻辑和Reed-Muller(RM)逻辑来表示[3].与传统的布尔逻辑电路相比,基于RM逻辑的电路在功耗和面积等方面具有巨大的优势.此外,用RM逻辑表示的电路可测性更强,电路结构更加紧凑[4-5].固定极性(Fixed-Polarity Reed-Muller, FPRM)是RM逻辑常用的表达方式.在三值FPRM逻辑函数中,n变量函数有3n个固定极性,对应于3n个不同的三值FPRM表达式,其表达式的复杂程度由极性决定.因此,极性对三值FPRM电路的功耗和面积等性能产生了很大的影响.对较小规模的电路进行优化时,可用穷举法遍历每个极性,但在优化较大规模电路时,由于极性与变量存在指数关系，使得搜索空间急剧增加,穷举法很难在有限的时间内得到优化结果[6].因此,需要寻求一种高效智能算法来提高搜索效率,以便尽快得到三值FPRM电路的最优或近最优极性.

模拟退火遗传算法[7]是一种改进型的遗传算法.单纯的遗传算法局部寻优能力差,容易出现早熟现象[8].将模拟退火算法引入到经典遗传算法中,结合2种算法的优化操作,可以提高算法的全局搜索能力,大大提高算法的效率.笔者通过研究三值FPRM逻辑表达式和模拟退火遗传算法,提出了一种基于模拟退火遗传算法的三值FPRM电路功耗优化方法.

1三值FPRM表达式及极性转换技术

1.1三值FPRM表达式

任何n变量的三值FPRM表达式都可表示为如下形式[9]:

(1)

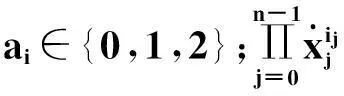
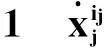
表查找表

1.2三值FPRM极性转换技术

国内外许多专家学者对多值RM逻辑尤其对RM逻辑极性转换进行了研究[10-12].极性转换包括Boolean逻辑展开式到RM逻辑展开式的转换和RM逻辑展开式不同极性间的转换.矩阵转换法(Matrix Transformation Method)和图形转换法(Map Transformation Method)是常用的多值FPRM极性转换方法.然而上述2种极性转换方法速度慢、时间复杂度大.文献[12]提出了一种三值FPRM极性转换算法,能有效提高转换速度.其基本过程表述如下:

(1)极性初始化:随机产生一个极性p,并用三进制表示p=(p1,p2,…,pn);

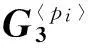
(4)根据新项产生公式,每个最小项的新项为πi：

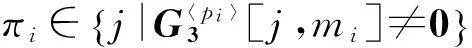
(2)

(5)根据贡献值计算公式：

(3)

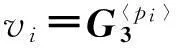
(6)对所有的最小项重复步骤(3)～(5),最后的累加值即为RM表达式系数.

表2　GF(3)互补变量和转换矩阵

2基于模拟退火遗传算法的三值FPRM电路功耗最佳极性搜索

2.1三值FPRM电路功耗估计模型

要实现三值FPRM电路功耗的最佳极性搜索,首先需要建立三值FPRM电路的功耗估计模型.分析式(1)可知,三值FPRM逻辑函数由多输入模3加和模3乘运算组成,因此三值FPRM电路可以表示为由多输入模3加和模3乘门组成.多输入门的输入输出关系复杂程度不同,且在工艺上大多使用二输入门,所以在电路映射之前,往往需要把多输入模3加和模3乘门分解成一系列二输入模3加和模3乘门,因此三值FPRM电路的功耗可看成由二输入模3加和模3乘门引起.电路的开关活动性与功耗成正比,其值直接反映电路功耗的大小,因此可以用开关活动性表示电路的功耗.门电路的开关活动性可以用其输出端的信号概率表示.

假设信号x=1和x=2的概率为在一段足够长时间内测得信号x=1和x=2的时间与总的测量时间之比,分别记作Px1和Px2.根据模3加和模3乘运算的输入输出关系和信号概率传递规律,可以分别推出二输入模3加和模3乘门的输出信号概率.

图1　模3加和模3乘真值表Fig.1　The truth tables of modulo-3 addition and modulo-3 multiplication

二输入模3加门输出信号概率:

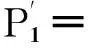
Px1·(1-Py1-Py2)+

(1-Px1-Px2)·Py1+Px2·Py2,

(4)

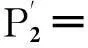
Px2·(1-Py1-Py2)+

1-Px1-Py1+(1-Px1+Px2)·Py2.

(5)

二输入模3乘门输出信号概率：

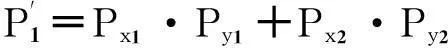
(6)

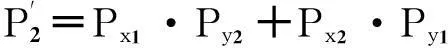
(7)

2.2模拟退火遗传算法

传统遗传算法只有子代参与竞争,子代和父代之间没有竞争关系,容易导致父代中优秀个体的缺失,出现早熟和局部寻优能力差等现象.模拟退火算法局部搜索能力强,能有效弥补遗传算法的缺陷.模拟退火遗传算法结合遗传算法和模拟退火算法的优点,并允许父代参与竞争,能有效提高算法的寻优能力.

2.2.1构建适应度函数

本文搜索的三值FPRM电路功耗最佳极性为一个整数值,因此可以用其三进制形式作为本算法的编码方式.在极性搜索过程中需要对极性进行评价,本文以功耗优化为目的,将极性对应的三值FPRM电路功耗作为评价标准,以此构建适应度函数.在模拟退火遗传算法中,适应度函数值越大表示个体越优秀,但功耗最佳极性要求功耗越小越好.因此,为了便于两者结合,采用功耗的倒数来表示适应度,设置适应度函数如下:

f(i)=(1/poweri)×b,

(8)

其中poweri表示对应极性下的三值FPRM电路功耗,b为放大系数.

2.2.2交叉和变异操作

交叉操作能把父代中的优秀基因遗传给下一代,是遗传算法中的一个重要操作,起核心作用.本文通过一致交叉方法实现交叉操作:首先以一定概率选取父代中的2个个体F1和F2,同时随机产生一个等长的二进制码A;然后根据父代个体和二进制码A产生2个子代个体S1和S2.交叉过程如图1所示:当二进制码A对应位为1时,子代S1继承父代F1的基因,子代S2继承父代F2的基因;当二进制码A对应位为0时,子代S1继承父代F2的基因,子代S2继承父代F1的基因.

图2　一致交叉操作Fig.2　The operation of uniform crossover

变异操作是遗传算法的另一个重要操作,表示种群中某些个体的基因发生了突变.变异操作是一种局部随机搜索,能防止算法早熟.本文变异操作的具体步骤为:以一个小概率选择需要变异的个体,随机产生变异位,变换变异位的值,变换规则为“0→1，1→2，2→0”.

2.2.3模拟退火选择操作

模拟退火选择操作是模拟退火遗传算法与传统遗传算法的不同之处,它允许父代参加竞争,使父代中的优秀个体得以保存.本文的模拟退火选择操作为:首先根据适应度值的大小对父代和子代进行排序;然后在父代和子代群体中各自选择适应度值最优的2w/3个个体,组成新的群体;最后对新群体进行退火选择,选取w个个体组成新的种群.个体i被选取的概率为:

(9)

其中,f(i)表示个体i的适应度值;Tk表示退火温度,Tk=1/ln(k/T0+1),k=1,2,…;w表示种群规模;T0表示起始温度.

2.3算法描述

算法的基本步骤:

(1)读入PLA格式的MCNC Benchmark电路,运用三值积之和表达式到三值FPRM表达式的转换技术,将三值最小项表达式转换到0极性下的三值FPRM表达式;

(2)生成父代种群:随机产生w个用三进制表示的整数,计算父代种群个体的适应度;

(3)生成子代种群:父代种群通过交叉和变异操作产生子代种群,计算子代种群个体的适应度;

(4)进行模拟退火选择操作产生新的父代种群,计算新的父代种群个体适应度;

(5)重复步骤(3)和(4),直到满足最大演化代数,输出最佳极性及其对应的电路功耗.

在进行最佳极性搜索之前需要读入PLA格式电路,然而目前只有标准的二值PLA格式电路,因此先用文献[13]所提方法将标准的二值PLA格式电路转换为三值PLA格式电路,然后运用上述所提算法进行最佳极性搜索.

3仿真结果与分析

本文所提算法在Windows 7 64位操作系统,Intel(R) Core(TM) i3-2130 CPU 3.40 GHZ, 4 G RAM运行环境下,用C语言通过VC6.0编译实现,随机选取13个MCNC Benchmark电路进行仿真,搜索到的最佳极性与0极性比较.为计算三值FPRM电路的开关活动性,随机产生15组输入信号概率:(P1,P2)={(0.21,0.53),(0.49,0.30),(0.33,0.24),(0.68,0.13),(0.15,0.26),(0.57,0.22),(0.18,0.51),(0.71,0.24),(0.08,0.35),(0.57,0.32),(0.46,0.28),(0.17,0.05),(0.32,0.43),(0.14,0.72),(0.25,0.61)}.

三值FPRM电路功耗最佳极性搜索结果如表3所示.其中,列1和列2分别为电路名称和输入/输出变量个数;列3～5分别表示0极性下二输入模3加的门数量、二输入模3乘的门数量和电路功耗;列6～9分别表示所提算法搜索到的最佳极性、最佳极性下三值FPRM电路二输入模3加的门数量、二输入模3乘的门数量和电路功耗.

表3　三值FPRM电路功耗的最佳极性搜索结果

与0极性相比，最佳极性在模3加的门数量、模3乘的门数量以及功耗上节省的百分比如表4所示.模3加的门数量、模3乘的门数量和功耗节省的百分比定义如下:

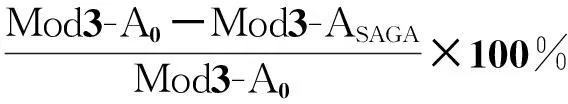
(10)

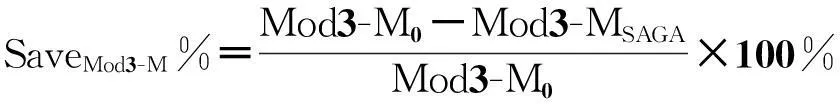
(11)

(12)

其中,SaveMod3-A、SaveMod3-M和SavePower分别表示模3加的门数量、模3乘的门数量和功耗的节省;Mod3-A0、Mod3-M0和Power0表示0极性下模3加的门数量、模3乘的门数量和功耗大小;Mod3-ASAGA、Mod3-MSAGA和PowerSAGA表示所提算法搜索到的最佳极性下模3加的门数量、模3乘的门数量和功耗大小.

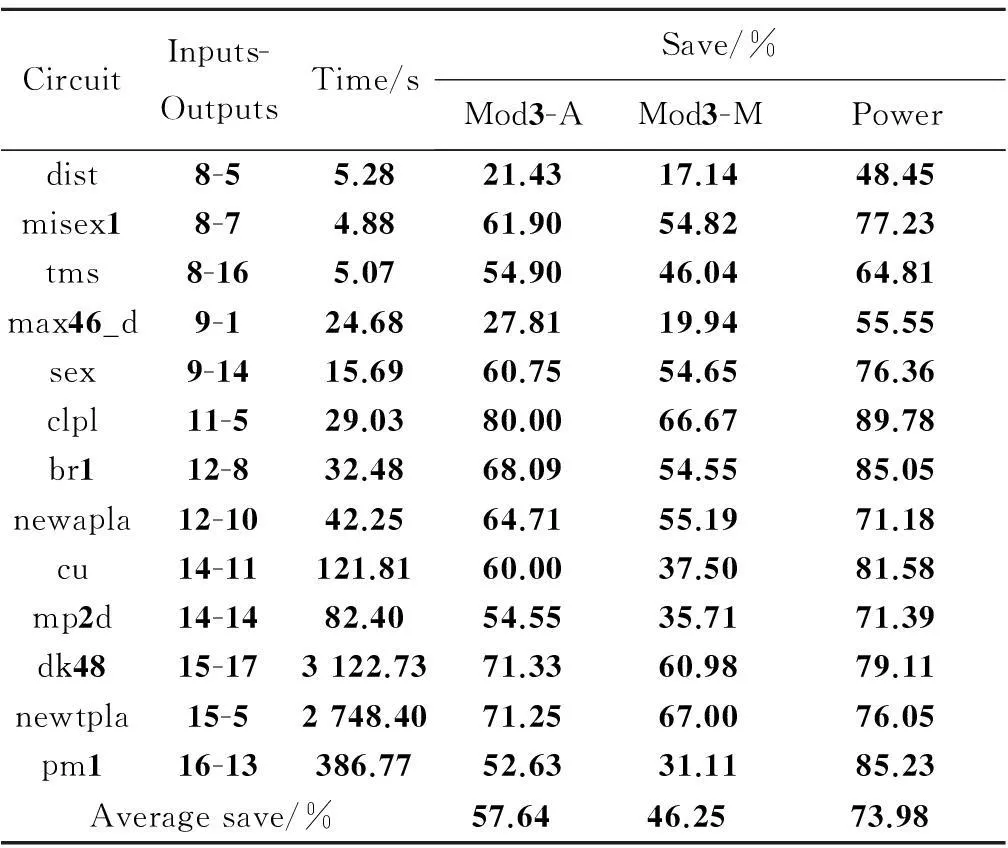
表4　三值FPRM电路门数和功耗节省百分比

分析数据可知,所提方法搜索到的最佳极性与0极性相比优化效果明显,其中clpl电路在模3加的门数量、模3乘的门数量和功耗上分别节省了80.00%,66.67%和89.78%,13个测试电路在模3加的门数量、模3乘的门数量和功耗上分别平均节省了57.64%,46.25%和73.98%.

4结论

通过对三值FPRM逻辑表达式的研究，建立了三值FPRM电路功耗估计模型,并结合三值FPRM极性转换技术,提出了一种基于模拟退火遗传算法的三值FPRM电路功耗最佳极性搜索方法.所提方法在Windows 7操作系统下,基于C语言通过VC6.0编译实现,对13个MCNC Benchmark电路进行仿真，结果表明,所提方法搜索到的最佳极性与0极性相比具有较好的优化效果.

参考文献(References)：

[1]郑雪松,汪鹏君,杨乾坤.基于绝热多米诺逻辑的三值移位寄存器设计[J].浙江大学学报：理学版,2014,41(4):427-431.

ZHENG Xuesong, WANG Pengjun, YANG Qiankun. Design of ternary shift register based on adiabatic domino logic[J]. Journal of Zhejiang University: Science Edition, 2014, 41(4): 427-431.

[2]汪鹏君,杨乾坤,郑雪松.三值绝热多米诺加法器开关级设计[J].电子与信息学报,2012,34(10):2514-2519.

WANG Pengjun, YANG Qiankun, ZHENG Xuesong. Design of ternary adiabatic domino adder on switch-level[J]. Journal of Electronics & Information Technology,2012, 34(10): 2514-2519.

[3]RAFIEV A, MOKHOV A, BUMS F P, et al. Mixed radix reed-muller expansions[J]. IEEE Transactions on Computers, 2012, 61(8): 1189-1202.

[4]Al JASSANI B A, URQUHART N, ALMAINI A E A. Manipulation and optimisation techniques for Boolean logic[J]. IET Computers & Digital Techniques, 2010, 4(3): 227-239.

[5]RAHAMAN H, DAS D K, BHATTACHARYA B B. Testable design of AND-EXOR logic networks with universal test sets[J]. Computers & Electrical Engineering, 2009, 35(5): 644-658.

[6]王振海,汪鹏君,俞海珍,等.基于PSO算法的FPRM电路延时和面积优化[J].电路与系统学报, 2012,17(5):75-80.

WANG Zhenhai, WANG Pengjun, YU Haizhen, et al. Delay and area optimization for FPRM circuits based on PSO algorithm[J]. Journal of Circuits and Systems, 2012, 17(5): 75-80.

[7]贾伟娜,刘顺兰.模拟退火遗传算法在DOA估计技术中的应用[J].Computer Engineering and Applications,2014, 50(12): 266-270.

JIA Weina, LIU Shunlan. Application of simulated annealing genetic algorithm in DOA estimation technique[J]. Computer Engineering and Applications, 2014, 50(12)：266-270.

[8]王小平,曹立明.遗传算法:理论,应用及软件实现[M].西安：西安交通大学出版社,2002.

WANG Xiaoping，CAO Liming. Genetic Algorithm: Theory, Application and Software Implementation[M]. Xi’an：Xi’an Jiaotong University Press，2002.

[9]FALKOWSKI B J, FU C. Polynomial expansions over GF (3) based on fastest transformation[C]//Proceedings of the 33rd International Symposium on Multiple-Valued Logic. Washington: IEEE Computer Society, 2003: 40-45.

[10]FALKOWSKI B J, FU C. Fastest classes of linearly independent transforms over GF (3) and their properties[J]. IEE Proceedings-Computers and Digital Techniques,2005, 152(5): 567-576.

[11]FU C, FALKOWSKI B J. Ternary fixed polarity linear Kronecker transforms and their comparison with ternary Reed Muller transform[J]. Journal of Circuits, Systems and Computers,2005, 14(4): 721-733.

[12]孙飞,汪鹏君,俞海珍.三值FPRM电路极性间转换算法及其在面积优化中的应用[J].浙江大学学报:理学版,2014,41(1):43-48.

SUN Fei, WANG Pengjun, YU Haizhen, et al. Ternary FPRM circuit conversion algorithm between polarities and its application in area optimization[J]. Journal of Zhejiang University: Science Edition, 2014, 41(1): 43-48.

[13]FALKOWSKI B J, LOZANO C C, RAHARDJA S. Column polarity matrix algorithm for ternary fixed polarity Reed-Muller expansions[J]. Journal of Circuits, Systems and Computers,2006, 15(2): 243-262.

The search of the best power polarity of ternary FPRM circuit based on simulated annealing genetic algorithm. Journal of Zhejiang University(Science Edition), 2016,43(2):190-194,199

Abstract:For n-variable ternary FPRM (Fixed-Polarity Reed-Muller) logic function, there are 3n fixed polarities. The power of ternary FPRM circuit with different polarities is different from each other. A scheme searching for the best polarity on the power of ternary FPRM circuit is proposed. Firstly, according to the ternary FPRM logic function expression and the switch signal transmission theory, a power estimation model for ternary FPRM circuit is established. Secondly, simulated annealing genetic algorithm (SAGA) is used to search for the best polarity, so as to get the best power consumption FPRM circuit. Finally, 13 MCNC benchmarks are used to verify the effectiveness of the proposed method. Results show that the optimized ternary FPRM circuits save 73.98% power in average than the corresponding FPRM circuits under polarity 0.

Key Words:ternary logic function; FPRM circuit; simulated annealing genetic algorithm; power consumption

中图分类号：TN 79

文献标志码：A

文章编号：1008-9497(2016)02-190-05

DOI:10.3785/j.issn.1008-9497.2016.02.012

作者简介：厉康平(1991-)，男，硕士研究生，主要从事高信息密度和低功耗集成电路理论及设计研究.*通信作者,ORCID:http://orcid.org/0000-0002-1461-3719,E-mail:wangpengjun@nbu.edu.cn.

基金项目：浙江省自然科学基金资助项目(LY13F040003)；国家自然科学基金资助项目(61234002，61306041).

收稿日期：2015-03-24.