巴拿赫空间上斜演化半流的非一致指数不稳定性的存在条件

岳　田, 宋晓秋

(1. 湖北汽车工业学院 理学院， 湖北 十堰 442002； 2. 中国矿业大学 理学院， 江苏 徐州 221116)



巴拿赫空间上斜演化半流的非一致指数不稳定性的存在条件

岳田1, 宋晓秋2

(1. 湖北汽车工业学院 理学院， 湖北 十堰 442002； 2. 中国矿业大学 理学院， 江苏 徐州 221116)

摘要：基于一致指数不稳定的定义，引入了Banach空间中斜演化半流非一致指数不稳定的概念，并用实例阐释了二者的关系.借助于指数稳定性的研究方法,讨论了斜演化半流非一致指数不稳定的特征，建立了其非一致指数不稳定的2个充要条件.所得结论推广了指数稳定性及一致指数不稳定性中的一些已有结果.

关键词：斜演化半流； 非一致指数不稳定性； 巴拿赫空间； 指数衰退

YUE Tian1, SONG Xiaoqiu2

(1.SchoolofScience,HubeiUniversityofAutomotiveTechnology,Shiyan442002,HubeiProvince,China; 2.CollegeofScience,ChinaUniversityofMiningandTechnology,Xuzhou221116,JiangsuProvince,China)

近年来，利用斜演化半流来研究无限维空间中演化方程的渐近性质取得了长足发展.关于斜演化半流的概念首先由MEGAN等[1]引入，与演化算子、演化族、斜积流仅依赖于2个变量不同,其依赖于3个变量，进而利用斜演化半流来研究演化方程解的渐近行为似乎更为合理，尤其是在指数稳定性方面.如文献[2]给出Banach空间中斜演化半流一致指数稳定的性质刻画，并得到了相应性质在一致集上的统一形式；文献[3]利用Banach函数空间及Banach序列空间分别给出了线性斜演化半流一致指数稳定的连续与离散特征；文献[4]给出了线性斜演化半流一致指数稳定的连续及离散型Barbashin定理；文献[5]则采用类似于文献[2]的方法，研究了斜演化半流非一致指数稳定的若干性质；文献[6]定义了斜演化半流指数及多项式稳定的若干形式，给出了相关概念间的关系，并得到了指数及多项式稳定的积分特征.

与指数稳定性相比，关于斜演化半流指数不稳定性(膨胀性)的研究相对较少.如文献[1]对斜演化半流的一致指数不稳定性进行了研究，得到了DATKO相应型结论[7]；文献[8]给出了与斜演化半流的弱指数膨胀性相关的性质，并利用Lyapunov函数刻画了弱指数膨胀的相关特征；文献[9]利用Banach函数空间及Banach序列空间分别给出了线性斜演化半流一致指数膨胀的充要条件.由于一致指数不稳定条件太强，本文将在上述文献的基础上，给出Banach空间中斜演化半流非一致指数不稳定性的概念，并探究其成立的一系列充要条件.

1预备知识

设(X,d)为一度量空间，V是一个Banach空间，将空间V上的范数及作用其上的有界线性算子全体B(V)上的范数记作‖·‖.记

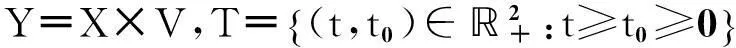
I为恒等算子.

定义1[1-2]映射φ:T×X→X称为X上的演化半流(evolutionsemiflow)，需满足以下2个性质：

(es1)φ(t,t,x)=x,∀(t,x)∈+×X；

(es2)φ(t,s,φ(s,t0,x))=φ(t,t0,x),∀(t,s),

(s,t0)∈T,∀x∈X.

定义2[1-2]如果满足如下性质：

(ec1)Φ(t,t,x)=I,∀(t,x)∈+×X；

(ec2)Φ(t,s,φ(s,t0,x))Φ(s,t0,x)=Φ(t,t0,x),∀(t,s),(s,t0)∈T,∀x∈X.

则称映射Φ:T×X→B(V)为演化半流φ上的演化上循环(evolutioncocycle).

定义3[1-2]映射C:T×Y→Y，

C(t,s,x,v)=(φ(t,s,x),Φ(t,s,x)v),

(1)

称为Y上的斜演化半流(skew-evolutionsemiflow)，其中Φ为演化半流φ上的演化上循环.

关于斜演化半流的例子可参阅文献[1-2]中的例子，此处省略.值得注意的是，C0半群、演化算子、演化族、斜积流均为斜演化半流的特殊情形.

定义4[2]如果对于∀(t0,x,v)∈+×Y，映射在[t0,∞)上可测，则称斜演化半流C=(φ,Φ)为强可测.

定义5[8]如果存在常数M≥1和ω>0使得

(2)

对∀(t,s),(s,t0)∈T及∀(x,v)∈Y成立，则称斜演化半流C=(φ,Φ)为指数衰退的(exponentialdecay).

(3)

对∀(t,s),(s,t0)∈T及∀(x,v)∈Y成立，则称斜演化半流C=(φ,Φ)为非一致指数不稳定(nonuniformlyexponentiallyinstable).

注 1斜演化半流C=(φ,Φ)是非一致指数不稳定的，当且仅当存在非减函数N:+→[1,∞)和常数α>0使得

(4)

对∀(t,t0,x,v)∈T×Y成立.

注2若定义6中N(t)=N≥1，则称斜演化半流C=(φ,Φ)是一致指数不稳定的(uniformlyexponentiallyinstable)[1]，显然若C是一致指数不稳定的，则一定是非一致指数不稳定的，反之不一定成立.

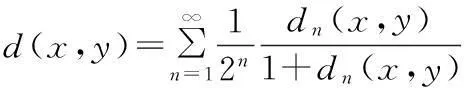
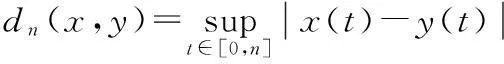
ft(τ)=f(t+τ),∀τ∈+.

则(X,d)为度量空间且映射

φ:T×X→X,φ(t,s,x)=xt-s

为X上的演化半流.令V=，考虑映射，其中ρ(t)=sint-tcost+2t，则其为一演化上循环，进而C=(φ,Φ)为斜演化半流.由于

ρ(t)-ρ(t0)=

sint-sint0-tcost+t0cost0+2t-2t0≥

t(1-cost)-t0(1-cost0)+t-t0-2≥

t-3t0-2，

进而可得

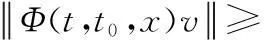
即

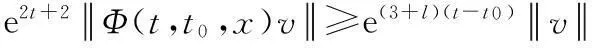
故C是非一致指数不稳定的.

假设C是一致指数不稳定的，则存在常数N≥1和α>0使得对∀(t,t0,x,v)∈T×Y，

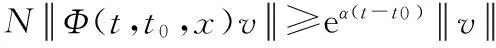
现取t=2nπ+2π，t0=2nπ+π，则

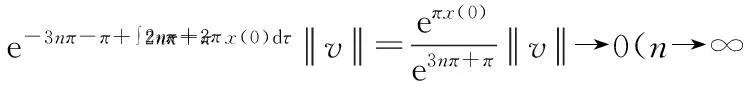
从而矛盾，故C非是一致指数不稳定的.

2主要结论

定理1斜演化半流C=(φ,Φ)是非一致指数不稳定的当且仅当存在两非减函数f,g:+→[1,+∞)且g(t)=∞，使得

(5)

对∀(t,s),(s,t0)∈T，∀(x,v)∈Y成立.

证明必要性：取g(t)=eαt,∀t≥0即可证.

充分性：设(t,s)∈T，δ>0且满足g(δ)>1.则存在n∈和r∈[0,δ)，使得t-s=nδ+r.记

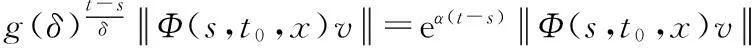
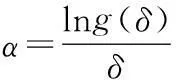
定理2设C=(φ,Φ)为一强可测的具有指数衰退的斜演化半流，则如下命题等价：

(i)C是非一致指数不稳定的；

(ii)存在非减函数ε:+→[1,∞)及常数v>0，使得对∀(t,t0,x,v)∈T×Y，式(6)成立.

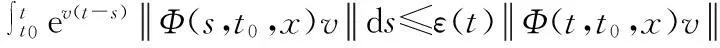
(6)

(iii)存在非减函数ε:+→[1,∞)使得对∀(t,t0,x,v)∈T×Y，式(7)成立.

(7)

证明(i)⟹(ii)由定义6知，对∀(t,s),(s,t0)∈T，∀(x,v)∈Y，存在非减函数N:+→[1,∞)和常数α>0，使得

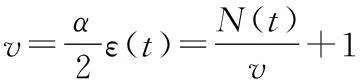
成立.

(ii)⟹(iii)显然.

(iii)⟹(i)因为C具有指数衰退性，故存在常数M≥1和ω>0使得对∀(t,s),(s,t0)∈T，∀(x,v)∈Y，

(8)

成立.进一步，

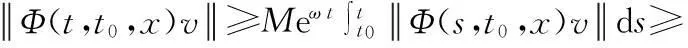
(9)

结合式(8)、(9)，对∀(t,t0,x,v)∈T×Y，

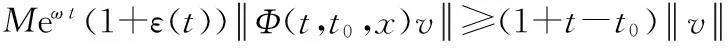
利用定理1，取f(t)=Meω t(1+ε(t))，g(t)=1+t，可得C=(φ,Φ)是非一致指数不稳定的.

参考文献(References)：

[1]MEGAN M, STOICA C. Exponential instability of skew-evolution semiflows in Banach spaces[J]. Stud Univ Babes-Bolyai Math,2008,53(1):17-24.

[2]STOICA C, MEGAN M. On uniform exponential stability for skew-evolution semiflows on Banach spaces[J]. Nolinear Analysis,2010,72(3/4):1305-1313.

[3]HAI P H. Continuous and discrete characterizations for the uniform exponential stability of linear skew-evolution semiflows[J]. Nolinear Anal,2010,72(12):4390-4396.

[4]HAI P H. Discrete and continuous versions of Barbashin-type theorems of linear skew-evolution semiflows[J]. Appl Anal,2011,90(12):1897-1907.

[5]STOICA C, MEGAN M. On nonuniform exponential stability for skew-evolution semiflows in Banach spaces[J]. Carpathian J Math,2013,29(2):259-266.

[6]STOICA C, BORLEA D. Exponential stability versus polynomial stability for skew-evolution semiflows in infinite dimensional spaces[J]. Theory Appl Math Comput Sci,2014,4(2):221-229.

[7]DATKO R. Uniform asymptotic stability of evolutionary processes in Banach spaces[J]. SIAM J Math Anal,1972,3(3):428-445.

[8]YUE T, SONG X Q, LI D Q. On weak exponential expansiveness of skew-evolution semiflows in Banach spaces[J]. J Inequal Appl,2014(1):1-11.

[9]YUE T, LEI G L, SONG X Q. Some characterizations for the uniform exponential expansiveness of linear skew-evolution semiflows[J]. Advances in Mathematics (China),2015,45,doi:10.11845/sxjz.2014173b.

Criteria for the existence of nonuniform exponential instability of skew-evolution semiflows in Banach spaces. Journal of Zhejiang University(Science Edition), 2016,43(2):181-183

Abstract:Based on the definition of uniform exponential instability, a skew-evolution semiflow with nonuniform exponential instability is presented in Banach spaces. An illustrating example is used to clarify the relationship between the two concepts. Exponential stability technique is applied to study the features of nonuniform exponential instability of skew-evolution semilflows. Two necessary and sufficient conditions concerning the nonuniform exponential instability of skew-evolution semiflows are given. The obtained conclusions are generalizations of the well-known results about the exponential stability and uniform exponential instability.

Key Words:skew-evolution semiflow; nonuniform exponential instability; Banach space; exponential decay

中图分类号：O 175.13

文献标志码：A

文章编号：1008-9497(2016)02-181-03

DOI:10.3785/j.issn.1008-9497.2016.02.010

作者简介：岳田(1988-)，ORCID:http://orcid.org/0000-0002-3371-5673,男，助教，硕士，主要从事微分系统的渐近行为研究,E-mail: ytcumt@163.com.

基金项目：湖北省自然科学基金资助项目(2014CFB629); 湖北汽车工业学院校预研基金项目(2014CFB629).

收稿日期：2015-08-06. 2015-08-06.