得分信息下考虑不确定心理行为的双边匹配

乐　琦

(江西财经大学 信息管理学院, 江西 南昌 330013)



得分信息下考虑不确定心理行为的双边匹配

乐琦

(江西财经大学 信息管理学院, 江西 南昌 330013)

摘要：从不确定心理行为的角度研究得分信息下的双边匹配问题．首先将期望得分视作参照点，计算了得分的相对收益，进而构建了收益矩阵；再根据TODIM理论，将收益矩阵转换为价值矩阵；进一步，构建了匹配模型；通过求解模型得到匹配方案；供需匹配实例说明了所提方法的有效性．

关键词：双边匹配；得分；不确定心理行为；TODIM

YUE Qi

(SchoolofInformationManagement,JiangxiUniversityofFinanceandEconomics,Nanchang330013,China)

双边匹配问题涉及如何匹配双方离散的主体，其中每个主体都对另一方主体给出自身偏好．在现实生活中，稳定婚姻问题[1]、报业匹配问题[2]、大学招生问题[3]、IT服务外包匹配问题[4]等均为双边匹配问题，应用前景十分广阔．更合理的匹配方案有利于提升匹配双方的社会活动效率及满意度．因此，以双边匹配为主题的研究具有重要的理论和现实意义．

近年来，基于序数和得分信息的双边匹配问题，受到了学者们的广泛关注[5-11]．例如，为了解决基于不完全得分信息的双边匹配问题，文献[5]提出了以满意度最大化为目标的匹配模型．文献[6]针对基于得分信息的双边匹配问题，提出了一种决策方法．文献[7]针对不确定得分环境下的双边匹配问题，提出了相应的匹配方法．文献[8]针对严格得分信息下的匹配问题，着重分析了如何得到稳定匹配．文献[9-10]从主体心理行为的视角研究了基于序数信息的双边匹配问题．此外，文献[12-15]从图论角度出发，研究了相关匹配问题中的几何结构和表示形式．

已有研究促进了双边匹配问题的相关理论、方法及实际应用的发展．但针对主体给出的偏好为得分信息的相关研究较少．另一方面，在大部分相关研究中，主体多被看作是完全理性的；而现实匹配过程刚好相反[16]．基于此，本文在文献[6,9-10]的基础上，进一步考虑有限理性表现为双方主体的不确定心理行为，本文着重研究得分信息下考虑不确定心理行为的双边匹配问题．

1符号描述

针对得分信息下考虑不确定心理行为的双边匹配问题，在文献[9-10,17]的基础上，给出有关变量的符号说明如下：

M={1,2,…,m}：下标1,2,…,m的集合；

N={1,2,…,n}：下标1,2,…,n的集合；

P={P1,P2,…,Pm}：P方主体集合，m≥2；

Pi：集合P的第i个元素，i∈M；

Q={Q1,Q2,…,Qn}：Q方主体集合，n≥m；

Qj：集合Q的第j个元素，j∈N；

SP：集合P到Q的得分集合，SP={s0,s1,…,snp}；

SQ：集合Q到P的得分集合，SQ={s0,s1,…,snq}；

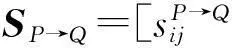
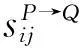
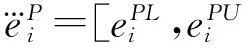
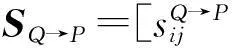
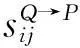
ΓTwo：匹配主体对集合(双方主体对形式)；

ΓOne：单身主体对集合(Q方主体对形式)；

Γ：双边匹配，Γ=ΓTwo∪ΓOne．

2双边匹配

2.1建立价值矩阵

考虑到期望得分能够反映双方主体预期的心理感受，且当作参照点能够较好地继承前景理论的多种性质[9-10]，因此这里选择期望得分为双方主体的参照点．

(1)

(2)

(3)

(4)

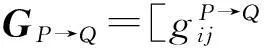
(5)

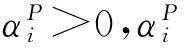
(6)

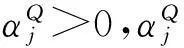
2.2建立匹配模型

(7a)

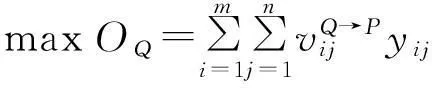
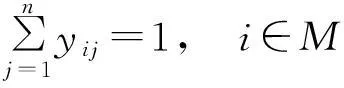
(7b)

s.t.,

(7c)

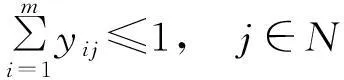
(7d)

yij∈{0,1},i∈M,j∈N．

(7e)

2.3求解匹配模型

采用线性加权法求解．设wP(wQ)表示ZP(ZQ)的权重，满足wP,wQ≥0，wP+wQ=1，则可将匹配模型(7)转换为匹配模型(8)

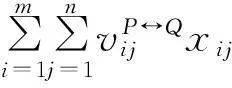
，　(8a)

s.t.,

(8b)

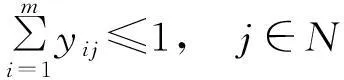
(8c)

yij∈{0,1},i∈M,j∈N,

(8d)

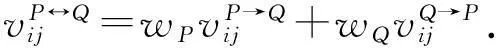
注4权重wP和wQ可由中介依据双边主体的地位来确定[17]．

2.4实施步骤

基于上述分析，得分信息下考虑不确定心理行为的双边匹配的实施步骤如下：

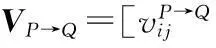
步骤4运用线性加权法，将匹配模型(7)转换为匹配模型(8)；

步骤5求解匹配模型(8)，得到双边匹配Γ．

3算例分析

以供需匹配问题为例，说明所提出方法的实用性．

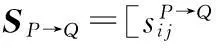
表1　完全得分矩阵SP→Q和期望得分

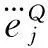
表2　完全得分矩阵SQ→P和期望得分

为说明本文所提方法的实用性，简单给出如下过程分析．

表3　系数矩阵V

为进一步说明本文所提方法的意义，进行如下过程分析．

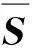
表4　系数矩阵

表5　双边匹配Γ*对比分析

4结论

从不确定心理行为的视角，研究了得分信息下的双边匹配问题．将期望得分当作参照点，计算了得分的相对收益；根据TODIM理论计算了感知价值，进一步，构建了匹配模型．得到：不确定心理行为影响双边匹配的确定；鉴于在实际匹配中有限理性的主体占据绝大多数，所提方法能更有效地反映双方主体的匹配行为．

参考文献(References)：

[2]CHANDRA A, COLLARD-WEXLER A. Mergers in two-sided markets: An application to the Canadian newspaper industry[J]. Journal of Economics & Management Strategy,2009,18(4):1045-1070.

[3]BRAUN S, DWENGER N, KÜBER D, et al. Implementing quotas in university admissions: An experimental analysis[J]. Games and Economic Behavior,2014,85(1):232-251.

[4]陈希,樊治平.考虑满意度交互的IT服务外包匹配决策方法[J].工业工程与管理,2012,17(2):90-96.

CHEN Xi, FAN Zhiping. A matching decision method in IT service outsourcing considering interactive satisfaction degree information[J]. Industrial Engineering and Management,2012,17(2):90-96.

[5]乐琦.基于不完全得分信息的双边匹配决策方法[J].系统工程,2013,31(9):79-83.

YUE Qi. Decision method for two-sided matching based on incomplete score information[J]. Systems Engineering,2013,31(9):79-83.

[6]乐琦.基于得分信息的双边匹配决策方法[J].模糊系统与数学,2014,28(1):106-112.

YUE Qi. Decision method for two-sided matching based on score information [J]. Fuzzy Systems and Mathematics, 2014,28(1):106-112.

[7]YUE QI. Two-sided matching decision under uncertain score environment[J]. International Journal of Multimedia and Ubiquitous Engineering,2014,9(12):193-202.

[8]YUE QI. Decision method for stable matching based on strict score information[J]. Advances in Information Sciences and Service Science,2013,5(10):1018-1025.

[9]乐琦,张磊,王中兴.不完全序值信息下考虑主体心理行为的匹配决策[J].模糊系统与数学,2014,28(4):90-99.

YUE Qi, ZHANG Lei, WANG Zhongxing. Matching decision considering agents’ psychological behavior with incomplete ordinal number information[J]. Fuzzy Systems and Mathematics,2014,28(4):90-99.

[10]乐琦.考虑主体心理行为的双边匹配决策方法[J].系统工程与电子技术,2013,35(1):120-125.

YUE Qi. Decision method for two-sided matching considering agents’ psychological behavior [J]. Systems Engineering and Electronic,2013,35(1):120-125.

[11]樊治平,李铭洋,乐琦.考虑稳定匹配条件的双边满意匹配决策方法[J].中国管理科学,2014,22(4):112-118.

FAN Zhiping, LI Mingyang, YUE Qi. Decision analysis method for two-sided satisfied matching considering stable matching condition[J]. Chinese Journal of Management Science,2014,22(4):112-118.

[12]LI Q L, SHIU W C, YAO H Y. Matching preclusion for cube-connected cycles[J]. Discrete Applied Mathematics,2015,190/191(20):118-126.

[13]ALOUPIS G, BARBA L, LANGEMAN S, et al. Bichromatic compatible matchings[J]. Computational Geometry, 2015, 48(8):622-633.

[14]BABU J, CHANDRAN L S, VAIDYANATHAN K. Rainbow matchings in strongly edge-colored graphs[J]. Discrete Mathematics,2015,338(7):1191-1196.

[15]LAMT. The uncrossing partial order on matchings is Eulerian[J]. Journal of Combinatorial Theory: Ser A,2015,135(1):105-111.

[16]BARTCZAK A, CHILTON S, MEYERHOFF J. Wildfires in poland: The impact of risk preferences and loss aversion on environmental choices[J]. Ecological Economics,2015,116(4):300-309.

[17]樊治平,乐琦.基于完全偏好序信息的严格双边匹配方法[J].管理科学学报,2014,17(1):21-34.

FAN Zhiping, YUE Qi. Strict two-sided matching method based on complete preference ordinal information[J]. Journal of Management Sciences in China,2014,17(1):21-34.

Two-sided matching considering uncertain psychological behavior with score information. Journal of Zhejiang University(Science Edition), 2016,43(2):242-246

Abstract:This paper investigates the two-sided matching problem with scores from view of uncertain psychological behavior. Firstly, the expectation scores are chosen as the reference points, and the relative gains corresponding to scores are calculated. So, the gain matrixes are built. According to the theory of TODIM, the gain matrixes are converted into the value matrixes. Furthermore, a matching model is developed. The matching alternative is obtained by solving the model. The example for the demander-supplier matching illustrates the good validity of the proposed method.

Key Words:two-sided matching; score; uncertain psychological behavior; TODIM

中图分类号：C 934

文献标志码：A

文章编号：1008-9497(2016)02-242-05

DOI:10.3785/j.issn.1008-9497.2016.02.021

作者简介：乐琦(1983-)，ORCID:http://orcid.org/0000-0001-9821-5859,男，副教授，博士，主要从事决策理论与方法研究,E-mail:yueqichina@126.com.

基金项目：国家自然科学基金资助项目(71261007，71261006，71462015，71361021，71363022)；江西省自然科学基金资助项目(20151BAB201026)；江西财经大学2014年度校级课题(K06492015).

收稿日期：2015-06-09.