基于工作空间最大化的2-RPC/2-SPC并联机构多学科设计优化

杜晴晴, 郭宗和, 王德军

(山东理工大学 机械工程学院， 山东 淄博 255049)



基于工作空间最大化的2-RPC/2-SPC并联机构多学科设计优化

杜晴晴, 郭宗和, 王德军

(山东理工大学 机械工程学院， 山东 淄博 255049)

摘要：以2-RPC/2-SPC并联机构为研究对象，首先考虑奇异位形、杆长、运动副转角等影响因素，采用数值法求解机构的工作空间；然后运用Isight软件对工作空间进行试验设计，得到工作空间达到较大时结构参数的取值范围；最后建立以机构灵巧度、静刚度、承载能力及驱动力为性能评价指标的多学科设计优化模型，基于Isight软件对模型进行求解使这些性能达到整体最优，得到结构参数的最优解，并对性能评价指标的结果进行可靠性评价.研究结果表明，多学科设计优化应用在并联机构是可行的，能为并联机构的优化设计奠定基础.

关键词：工作空间; 性能评价指标; 多学科设计优化

多学科设计优化因其具有能够协调多学科之间的复杂关系在航空航天领域取得了成功应用[1-3].目前，已经逐渐开始应用于汽车、船舶等工业，具有广阔的发展前景[4].Isight是应用最为广泛的多学科设计优化软件，封装有多种优化算法，可以集成各学科的专业应用软件建立多学科设计优化模型，并且能实时监控，可形成一个自动化、可视化的优化设计平台[5].

并联机构具有刚度大、运动精度高、承载能力强等优点，在实际工程中被广泛应用.并联机构的优化设计涉及到多个学科的耦合，因此，其不再局限于单一学科，而是对多个学科进行综合、协调、优化[6].大多数学者采用遗传算法对并联机构进行优化设计，运用Matlab软件进行求解.该方法算法单一、运算量大、操作较复杂.本文以一种四自由度并联机构为研究对象，运用Isight软件对机构进行多学科设计优化，以弥补传统方法的不足，为并联机构的优化设计奠定基础.

12-RPC/2-SPC并联机构

2-RPC/2-SPC并联机构由动平台A1A2A3A4、定平台D1D2D3D4、4条支链L1、L2、L3、L4组成.其中动、定平台均为矩形，驱动副为4条支链上的移动副.在动、定平台的质心位置建立空间直角坐标系p-uvw，O-XYZ，w、Z轴分别垂直于动、定平台所在的平面，方向向上，u、X轴分别平行于动平台、定平台的边A1A2、D1D2，v、Y轴由右手法则确定，如图1所示.设动、定平台的边长如下：LA1A4=2M, LA1A2=2N,LD1D2=2A, LD1D4=2B, 其中M,N,A,B为设计变量.

(a)结构简图　　　　　　　　　　(b)模型图图1　2-RPC/2-SPC并联机构的结构

22-RPC/2-SPC并联机构的工作空间

2.1工作空间的影响因素

分析2-RPC/2-SPC并联机构的工作空间时主要考虑下列因素：奇异位形、杆长限制、运动副限制[7].

(1)奇异位形：参考文献[8]对2-RPC/2-SPC并联机构奇异位形的分析.

(2)杆长限制：设定杆长Li的取值范围为

240mm ≤ Li≤ 400mm(i=1～4)

(3)运动副限制

首先对RPC支链进行分析：这里以支链1为例，设定支链1与定平台链接的转动副转角范围为[π/65π/6].这个转角可以用θ1,1表示，它代表向量O1B1与B1C1之间的夹角.求得

(1)

因此，需满足π/6≤θ1,1≤5π/6.

支链1与动平台链接处的圆柱副可以分解为1个转动副和1个移动副.转动副的求解同θ1,1，而移动副移动范围需满足-M≤YC1≤M.

然后对SPC支链进行分析：这里以支链2为例，设定支链2所在的直线与定平台所在的平面之间的夹角的范围为[π/65π/6]，这个夹角可以用θ2,1表示，求得

(2)

因此需满足π/6≤θ2,1≤5π/6.同样，支链2与动平台链接处的圆柱副可以分解为1个转动副和1个移动副.这个转动副的转角为θ2,2，求得

(3)

同样需满足π/6≤θ2,2≤5π/6.而移动副的移动范围需满足XA2≤XC2≤XA1，或XA1≤XC2≤XA2即

2.2机构的工作空间

本文采用数值法，给定动平台参考点的范围，利用位置反解进行搜索，并考虑工作空间的影响因素，运用Matlab编程计算“点集”近似衡量位置工作空间的大小.

设动、定平台结构参数的尺寸为：M=220mm，N=240mm，A=200mm，B=110mm.设定动平台参考点的范围如下：

-100mm≤Xp≤100mm,-100mm≤Yp≤100mm,100mm≤Zp≤240mm,-π/6≤β≤π/6.

求解得到机构的工作空间，如图2所示.

图2　2-RPC/2-SPC并联机构的工作空间

3机构工作空间的试验设计

针对并联机构的工作空间相对较小这个问题，运用 Isight对2-RPC/2-SPC并联机构的工作空间进行试验设计，使其工作空间相对较大.根据上文对工作空间的分析，得到设计变量即机构结构参数的取值范围为

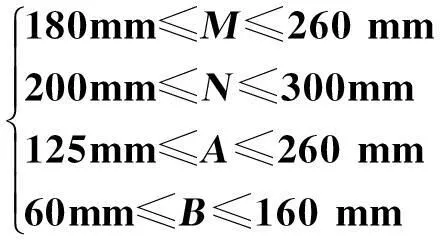
目标函数为工作空间内可行点的数量，用P表示.在Isight中选取任务组件Task，并集成实验设计方法组件DOE与Matlab组件.试验设计流程如图3所示. 在DOE组件中，选择拉丁超立方设计方法，样本点50个.

图3　工作空间试验设计流程

图4　设计变量对目标函数的主效应图

经过运算可得所有设计变量对目标函数的主效应图，如图4所示.从主效应图可见， 工作空间可行点数P随着A的增大而逐渐减小，B、M对P无影响，而N对P的影响程度最大，P随着N的增大而增大.因此，要想获得较大的工作空间，需减小A的取值，同时增大N的取值.

4机构的性能评价指标

4.1灵巧度

灵巧度是衡量机构运动传递失真程度的指标[9-10].灵巧度的分析主要基于速度雅可比矩阵，如雅可比条件数指标、可操作度指标.

雅可比矩阵的条件数可以定义为

(4)

可操作度指标可以表示为

(5)

将两种指标综合考虑，建立综合评价指标η来考察机构的灵巧度.

η=η1kJ+η2/w

(6)

式中：η1、η2分别为权重系数，可将权重系数设定不同的值，分别为η1=0.6，η1=0.4.

4.2承载能力

根据文献[11]所述，机构最大承载能力σFmax和最小承载能力σFmin分别为：

(7)

式中G与速度雅可比有直接关系，即G=(JT)-1.

(8)

4.3静刚度

静力学的求解一般是建立在刚度矩阵的基础上[12-13]，通过理论计算求解施加载荷与动平台末端的位移量之间的关系.

F=JT·KJ·J·Δx

(9)

式中：F表示末端执行器上的力或力矩向量；KJ是并联机构的关节刚度矩阵，KJ=diag[k1,k2,k3,k4]，其中ki表示每个驱动器的关节刚度，设定ki=10N/mm，F=10N；Δx表示动平台的微小位移.令

K=JT·KJ·J

(10)

动平台的位移可以表示为

Δx=K-1F

(11)

将Δx作为衡量机构静刚度的性能评价指标.

4.4驱动器的驱动力

在并联机构运动过程中，需要考虑各支链的运行速度、加速度、关节驱动力在允许的范围内.为此定义关节驱动力性能指标[14].

(12)

5机构的多学科设计优化

5.1多学科设计优化模型的建立

多学科设计优化模型的建立需要设定设计变量、约束条件、优化目标.

设计变量是根据工作空间试验设计的结果而定的，结构参数的变化范围如下：

约束条件的范围如下：

优化目标如下:

5.2基于Isight的多学科设计优化

在Isight中搭建的并联机构多学科设计优化流程图.如图5所示.

在Isight中利用TaskPlan组件将DOE组件和Optimization组件进行组合.Isight自动将DOE组件计算得到的近似最优解传递给Optimization组件作为设计初始值，在DOE组件中，采用最优拉丁超立方设计方法，设置样本点数为30；在Optimization组件中，采用NSGA-Ⅱ优化算法，设置种群大小为4，遗传代数为20.

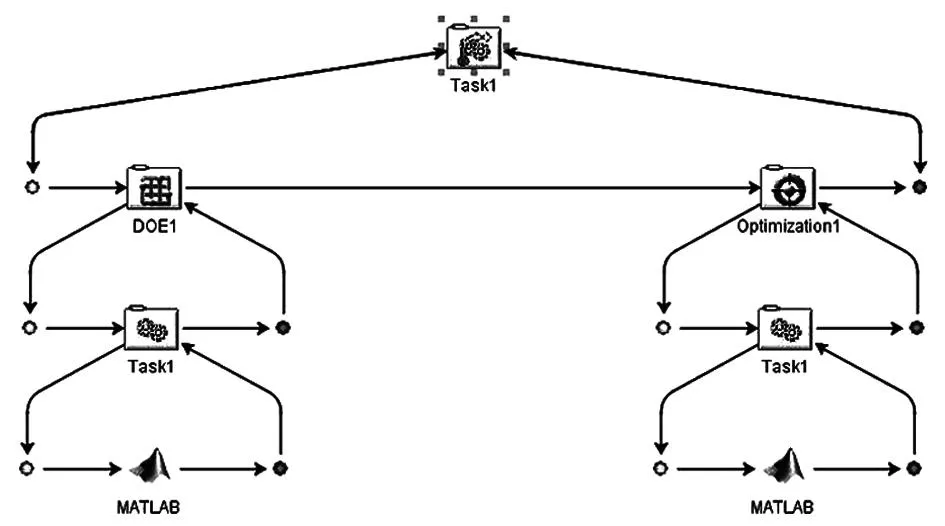
图5　2-RPC/2-SPC并联机构多学科设计优化流程

6结果分析

运用Isight对模型进行求解，可以得到所有设计变量对目标函数的主效应图，如图6所示.从主效应图可见，灵巧度、承载能力、静刚度随着设计变量A的增大而减小，而驱动力随着A的增大而增大；灵巧度、驱动力随着设计变量B的增大而增大，而承载能力、静刚度随着B的增大而减小，减小相对缓慢；灵巧度、驱动力随着设计变量M的增大而减小，而承载能力、静刚度随着M的增大而增大，增加相对缓慢；灵巧度、承载能力、静刚度随着设计变量N的增大而增大，而驱动力随着N的增大而减小.

(a) 灵巧度　　　　　　　　　　(b) 承载力

(c) 静刚度　　　　　　　　　(d) 驱动力图6　设计参数对目标函数的主效应图

运用Isight软件对设计变量进行取值计算时，都会记录下来并绘制成Pareto图，如图7所示，设计变量A、B、M、N的设计可行点用实心点表示，最佳设计点用十字线所在点表示.

最后可以得到Isight得出的设计参数的最优解如图8所示，Chengzaili(承载力)、Lingqiaodu(灵巧度)、Qudongli(驱动力)、Weiyiliang(表示静刚度)的最佳设计值分别为：26.41N，106.2，126.17N，1.69mm.

(a) 设计参数A　　　　　　　(b) 设计参数B

(c) 设计参数M　　　　　　　(d) 设计参数N图7　设计参数的设计可行点

图8　设计参数的最优解

7基于6Sigma的可靠性评价

为了验证多学科设计优化的结果是否可靠，有必要进行可靠性评价.在Isight中，对当前设计方案的可靠性评价是建立在6Sigma基础上的.在2-RPC/2-SPC并联机构的多学科设计优化模型基础上，将6Sigma组件添加到Task组件上，选择分析类型为“基于可靠性评估方法”ReliabilityTechnique，选择“均值算法”MeanValueMethod.

经过计算可以得出优化目标的概率分布及Sigma水平显示图，如图9所示.6Sigma来源于“6σ”，它表示当前设计方案某一性能指标的均值与质量约束之间的距离为±6σ，对应的可靠度为99.9%.从图9中可以看出，灵巧度、承载能力、静刚度与驱动力对应的可靠度为8σ，接近100%.所以，2-RPC/2-SPC并联机构多学科设计优化结果的可靠度非常高.

(a) 灵巧度　　　　　　　　(b) 静刚度

(c) 承载力　　　　　　　　(d) 驱动力图9　优化目标的概率分布及Sigma水平

8结论

(1)考虑奇异位形、杆长、运动副转角等影响因素，运用Isight软件对工作空间进行试验设计，使得并联机构在给定结构参数的取值范围内具有较大的工作空间.

(2)将多学科设计优化软件Isight应用到并联机构的优化设计中，综合考虑并联机构工作灵巧度、承载能力、静刚度与驱动力等多方面性能要求，以2-RPC/2-SPC并联机构为例，构建多学科设计优化基本流程与实现平台，为并联机构的优化设计奠定了基础.

(3)基于Isight软件，利用试验设计分析并联机构，并绘制主效应图，分析得到设计变量对优化目标的影响程度，为并联机构制造精度的控制提供了依据；利用多学科优化对由试验设计得出的近似模型进行优化，得到Pareto图，得到机构结构参数的最优解，并且可以得到满足条件的可行解供决策者根据不同需要进行选择.

参考文献:

[1]胡添元, 史士臣. 多学科设计优化在载人航天器构型设计中的应用研究[J]. 载人航天, 2013, 19(3)：91-96.

[2]KelaiaiaR,CompanyO,ZaatriA.MultiobjectiveoptimizationofalinerDeltaparallelrobot[J].MechanismandMachineTheory, 2012, 50：159-178.

[3]PerezRE,LiuHHT.Evaluationofmultidisciplinaryoptimizationapproachesforaircraftconceptualdesign[R].AIAA-2004-4537, 2004.

[4]WeckO,AgteJ,ArendsenP,etal.Sate-of-the-artandfuturetrendsinmultidisciplinarydesignoptimization[R].AIAA-2007-1905, 2007.

[5]赖宇阳.Isight参数优化理论与实例详解[M]. 北京：北京航空航天大学出版社, 2012.

[6]沈惠平, 张署, 刘安心, 等. 并联运动机械结构综合及其优化设计研究的最新进展[J]. 中国机械工程, 2009, 20(1)：118-125.

[7]SunT,SongYM,DongG.Optimaldesignofaparallelmechanismwiththreerotationaldegreesoffreedom[J].RoboticsandComputerIntergratedManufacturing, 2012, 28：500-508.

[8]朱松松, 郭宗和, 崔荣江, 等. 一种新型3T1R并联机构的设计与运动学分析[J]. 机械科学与技术, 2014, 33(2)：174-177.

[9]金国光, 王艳, 宋轶民, 等. 基于给定工作空间的球面变胞仿生关节机构优化设计[J]. 农业机械学报, 2013, 44(12)：288-293.

[10]于靖军, 刘辛军, 丁希仑, 等. 机器人机构学的数学基础[M]. 北京：机械工业出版社, 2008.

[11]崔国华, 周海栋, 王南, 等. 基于Isight的3-UPS-S并联机器人机构多目标优化[J]. 农业机械学报, 2013, 44(9)：261-266.

[12]季晔, 刘宏昭, 原大宁, 等. 一种四自由度并联机构I的性能指标分析[J]. 中国机械工程, 2012, 23(3)：258-263.

[13]李晓成, 高涛, 代小林. 重载冗余六自由度并联机构优化设计[J].机器人, 2013, 35(6)：731-735.

[14]窦玉超, 姚建涛, 高思慧, 等. 冗余驱动并联机器人动力学建模与驱动力协调分配[J]. 农业机械学报, 2014, 45(1)：293-299.

(编辑：郝秀清)

Multidisciplinary design optimization for 2-RPC/2-SPC parallel mechanism with respect to maximizing workspace

DU Qing-qing, GUO Zong-he, WANG De-jun

(School of Mechanical Engineering， Shandong University of Technology， Zibo 255049, China)

Abstract:Firstly, the influence of singularity equations, angle of motion pair and length of branched chain are considered to solve the workspace of the 2-RPC/2-SPC parallel mechanism. Secondly, the workspace is taken to design of experiments based on the Isight software in order to get the maximum workspace and obtain the optimal structure size. Finally, organization's dexterity, the carrying capacity, the static stiffness and the driving force are considered into establish the multidisciplinary design optimization model. The model is solved based on the Isight to obtain the optimal structure parameters under the overall optimal performance, and the results of the performance evaluation index are analyzed by the method of reliability evaluation. This research results show that it is feasible to apply the multidisciplinary design optimization method to optimal design of parallel mechanism and build a foundation for parallel mechanism from theory to the practical application.

Key words:workspace; performance evaluation index; multidisciplinary design optimization

中图分类号：TH112

文献标志码：A

文章编号：1672-6197(2016)04-0056-06

作者简介：杜晴晴，女，ganggangdu@126.com; 通信作者： 郭宗和，男，guozonghe@sdut.edu.cn

收稿日期：2015-04-27