钢板弹簧重叠部分应力及许用厚度计算理论的研究

宋　群， 周长城， 潘礼军

(山东理工大学 交通与车辆工程学院， 山东 淄博 255049)



钢板弹簧重叠部分应力及许用厚度计算理论的研究

宋群， 周长城， 潘礼军

(山东理工大学 交通与车辆工程学院， 山东 淄博 255049)

摘要：为满足叠加钢板弹簧解析拆分设计及CAD软件开发的要求，根据叠加钢板弹簧的力学模型，对钢板弹簧重叠部分等效厚度进行研究，并利用各片变形量、厚度与载荷之间关系，建立叠加钢板弹簧重叠部分等效厚度解析计算式.根据重叠部分等效厚度解析计算式和单片等效钢板弹簧应力公式，建立叠加钢板弹簧重叠部分应力及最大应力解析计算式.根据重叠部分的应力解析计算式和许用应力，建立许用厚度解析计算式.最后，通过实例对钢板弹簧重叠部分应力及许用厚度进行解析计算和ANSYS仿真验证.结果表明所建立的叠加钢板弹簧重叠部分应力及许用厚度的解析计算理论是正确的.

关键词：钢板弹簧； 应力； 许用厚度； 等效厚度； 解析计算

钢板弹簧由于结构简单、成本低廉、性能可靠、且能起到悬架导向转置和摩擦减振作用，因而成为汽车悬架中应用最广泛的一种弹性元件.目前，对于悬架钢板弹簧，大都是凭经验法和图解法进行设计，然后通过试验验证确定出弹簧的设计参数.尽管国内外很多学者曾对钢板弹簧变形和应力计算进行了大量研究，提出共同曲率法、集中载荷法、共同曲率与集中载荷综合法、有限单元法、CAE法等，但这些方法一直未给出满足钢板弹簧解析设计的应力计算式，因而制约了钢板弹簧CAD软件的开发.其中，共同曲率法[1]假设钢板弹簧面在长度方向上是相互完全贴合接触的，这一假设会导致弹簧叶片端点存在弯矩突变，最末几片应力误差较大.而集中载荷法计算短片应力具有较好的精度，但其余片应力却有较大的误差.共同曲率与集中载荷综合法[2-3]认为叠加钢板弹簧中间各片的载荷工况可分为“夹持约束部分”和 “非约束部分”，由于各片自由端处应力仍然按共同曲率方法计算，因而不满足相邻两片在端部重叠部分变形相等的约束条件.有限单元法[4-6]虽然在理论上是准确严密的，但其应力难以用简单的解析式表达，计算量很大.CAE仿真软件法[7]虽然可以得到可靠的仿真数值，但只能对给定结构的钢板弹簧在一定载荷下的应力进行数值仿真验证，而不能提供钢板弹簧的应力解析计算式.

本文将首先根据叠加钢板弹簧力学模型，对重叠部分的等效厚度进行研究，在此基础上对叠加钢板弹簧重叠部分的应力及最大应力和许用厚度解析计算进行研究，随后，对所研究的理论进行实例计算和仿真验证，从而建立可靠的应力解析计算理论，解决制约钢板弹簧解析设计的关键问题.

1叠加钢板弹簧的力学模型及重叠部分等效厚度解析计算式

钢板弹簧在实际行驶工况中的受力变形及接触状态非常复杂，其受力、变形及片间接触状态都是非线性的，难以进行理论分析得到解析计算式.为了建立叠加钢板弹簧解析计算式，必须对钢板弹簧的力学模型进行合理假设.由于在额定载荷情况下车辆悬架钢板弹簧是完全接触的，因此，假设钢板弹簧力学模型中的各片间完全接触且忽略片间摩擦.

1.1叠加钢板弹簧的力学模型

以一半叠加钢板弹簧为研究对象，设叠加钢板弹簧由n片不等长的簧片组成，各簧片宽度为b，簧片从第1片到第n片长度依次为L1，L2，…，Ln-1，Ln；对应的厚度依次为h1，h2，…，hn-1，hn，叠加钢板弹簧在自由端受到集中载荷F，如图1所示.

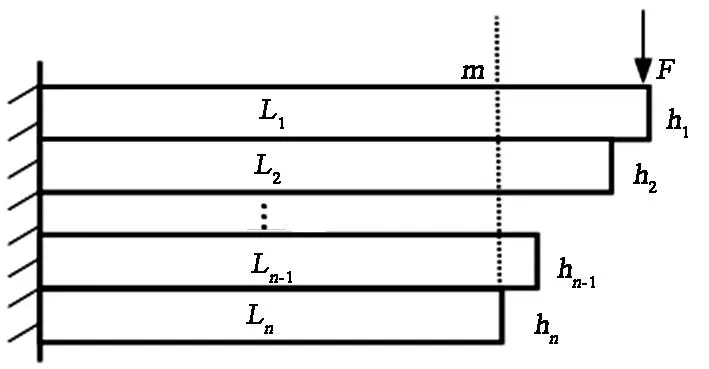
图1　多片叠加钢板弹簧力学模型

1.2叠加钢板弹簧重叠部分等效厚度解析计算式

为研究叠加钢板弹簧重叠部分等效厚度解析计算，将图1自由端处集中力F移至m处，即n片叠加钢板弹簧重叠部分端部，则n片叠加钢板弹簧力学模型等效为受集中力F和弯矩Mo=F(L1-Ln)的力学模型，如图2所示.图2中以叠加钢板弹簧重叠部分端部即m处为坐标原点，以原点左侧为正方向建立坐标系.n片叠加钢板弹簧重叠部分簧片可等效为单片钢板弹簧，其等效厚度为hez.

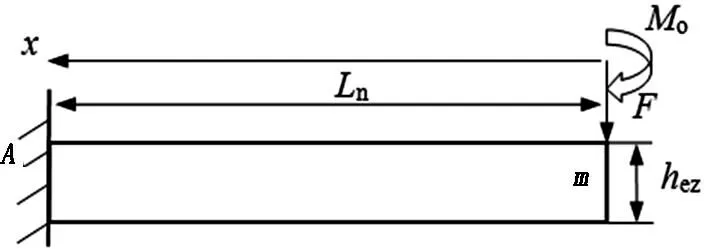
图 2　等效单片钢板弹簧的力学模型

根据材料力学知识[8]可知，钢板弹簧的变形微分方程为

(1)

式中:w为单片等效钢板弹簧的挠度；E为钢板弹簧的弹性模量；I为矩形截面惯性矩；M(x)为在x位置处的弯矩.

根据图2，任意x位置处截面的弯矩M(x)为

M(x)=Fx+Mo=(x+L1-Ln)F

(2)

式中，M0为集中力F移动到重叠部分端部m所产生的等效弯矩，Mo=(L1-Ln)F.

把式(2)代入变形微分方程(1)得

(3)

对式(3)进行两次积分，根据钢板弹簧固定端A处的边界约束条件，即变形量wA=0，转角wA′=0，可得常数C1和C2分别为

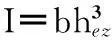
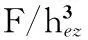
因此，钢板弹簧重叠部分的变形解析计算式，可简洁地表示为

(4)

由图1钢板弹簧受力情况可知，当钢板弹簧自由端受到集中力F和弯矩Mo时，叠加钢板弹簧各片所受力不相等，但是各片钢板弹簧承受力之和等于总的载荷，即

F1+F2+…+Fn=F

(5)

由图1钢板弹簧变形情况可知，多片叠加钢板弹簧重叠部分的弯曲变形量相等，且等于重叠部分单片等效钢板弹簧的弯曲变形量.因此，由钢板弹簧变形解析计算式(5)，可得

(6)

由式(5)和式(6)，可得多片叠加钢板弹簧重叠部分的等效厚度hez为

(7)

2叠加钢板弹簧重叠部分应力及最大应力和许用厚度解析计算式

2.1叠加钢板弹簧重叠部分应力及最大应力解析计算式

根据图2所示，单片等效钢板弹簧任意截面处应力为[11-12]

(8)

根据材料力学知识[6]可知，单片等效矩形截面钢板弹簧的抗弯截面系数W为

(9)

将式(2)、式(9)代入式(8)得单片等效钢板弹簧任意截面处应力为

(10)

由图2知，当x=Ln即在一半叠加钢板弹簧固定端A处，单片等效钢板弹簧应力取得最大值，即

(11)

由叠加钢板弹簧重叠部分变形解析计算式(6)可知，叠加钢板弹簧重叠部分各片所承受的载荷为

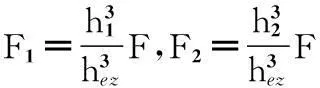
设各片钢板弹簧的当量厚度系数分别为

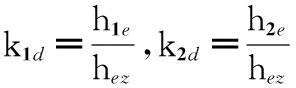
则各片钢板弹簧所承受的载荷分别可表示为

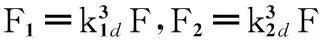
为了规避全球金融账户涉税信息自动交换过程中引发的纳税人信息维护的法律风险，全球金融账户涉税信息自动交换行动参与国应依托《协定公约》相关规范指引，借鉴欧盟和美国的经验，积极制定实施本国相关的纳税人权利保护法律制度，或者完善现行的纳税人权利保护制度，引入纳税人信息保护权利，高度关切保护纳税人信息的隐私权和知情权。

(12)

将式(12)代入到式(10)，可得叠加钢板弹簧重叠部分各片应力解析计算式为

(13)

由图2知，当x=Ln即在一半叠加钢板弹簧固定端A处，叠加钢板弹簧重叠部分各片应力取得最大值，即

(14)

由式(14)可知，叠加钢板弹簧最大应力出现在叠加钢板弹簧最厚的片上.

2.2叠加钢板弹簧许用厚度解析计算式

根据钢板弹簧材料属性，选取钢板弹簧的许用应力[σ].为保证多片叠加钢板弹簧满足强度要求，各片最大应力应小于许用应力，即

[σ1max，σ2max，…，σnmax]max<[σ]

由式(14)可知，叠加钢板弹簧的最大应力，一定出现在叠加钢板弹簧重叠部分最大厚度的固定端处.因此，叠加钢板弹簧的许用厚度[hi]max应满足

即叠加钢板弹簧的许用厚度为

(15)

利用式(15)便可对多片不等长叠加钢板弹簧的许用厚度进行计算，并且为钢板弹簧拆分设计奠定了重要的理论基础.

3叠加钢板弹簧重叠部分应力解析计算实例及ANSYS仿真验证

3.1叠加钢板弹簧重叠部分最大应力的解析计算实例

例如，某钢板弹簧总成由3片组成，其中，各片钢板弹簧的厚度和一半长度分别为：h1=15mm，L1=750mm；h2=12mm，L2=650mm；h3=10mm，L3=550mm.宽度b=30mm，一半集中载荷F=800N.

根据式(7)，可计算三片叠加钢板弹簧重叠部分的等效厚度为

根据叠加钢板弹簧重叠部分最大应力解式，叠加钢板弹簧最大应力发生在最厚一片钢板弹簧上，即最大应力出现在第1片钢板弹簧上

3.2叠加钢板弹簧重叠部分最大应力的ANSYS仿真验证

利用ANSYS有限元仿真软件，对实例中多片不等长叠加钢板弹簧建立仿真模型，仿真过程中忽略片间摩擦，设置钢板弹簧各片为No Separation的接触类型；以1.0mm为单位对模型划分网格；同时，设置钢板弹簧中心螺栓处为固定约束，卷耳侧为自由端，并在自由端施加一半载荷F=800N，对叠加钢板弹簧进行Von-Mises应力仿真分析.仿真得到的叠加钢板弹簧的应力云图如图3所示.

图 3　叠加钢板弹簧应力云图

根据图3可知，避开应力集中区域时，叠加钢板弹簧的仿真最大应力值为291.59MPa，与上述叠加钢板弹簧最大应力解析计算值295.16MPa相吻合，相对误差为1.2 %，结果表明所建立的叠加钢板弹簧应力解析计算式是正确的.

4结论

通过对多片叠加钢板弹簧的应力及最大应力和许用厚度的理论分析、实例计算与仿真验证，可知：

(1)通过对多片不等长叠加钢板弹簧重叠部分力学模型分析，利用叠加钢板弹簧重叠部分各片的变形量与其单片等效钢板弹簧的变形量相等原则，可建立叠加钢板弹簧重叠部分的等效厚度解析计算式.

(2)根据各片钢板弹簧变形量、厚度与载荷之间关系，可建立多片不等长叠加钢板弹簧重叠部分各片应力及最大应力的解析计算式.

(3)根据叠加钢板弹簧最大应力小于许用应力，可建立叠加钢板弹簧许用厚度解析计算式，为叠加钢板弹簧最大厚度的选取奠定了理论基础.

(4)由实例计算和仿真验证可知，不等长叠加钢板弹簧的最大应力解析计算值为295.16MPa，与ANSYS有限元软件的仿真验证值291.59MPa相吻合，相对偏差仅为1.2%，说明所建立的叠加钢板弹簧应力及最大应力和最大需用厚度解析计算方法是正确的、可靠的.

参考文献:

[1]郑银环.汽车钢板弹簧计算模型研究[D].武汉：武汉理工大学, 2005.

[2]窦宝华,张洪信,戴作强，等.钢板弹簧三自由度等效模型的应用与研究[J].制造业自动化,2014(12): 97-103.

[3]唐俊琦,朱晨虹.厚度对变截面钢板弹簧应力分布的影响[J].武汉理工大学学报,2014,38(4):914-918.

[4]邹海荣,黄其柏.国内外汽车钢板弹簧设计与分析方法的发展进程[J].上海汽车,2004(7):25-27.

[5]林金木.有限单元法解钢板弹簧[J].汽车工程, 1984(4):20-36.

[6]Savaidis G,Malikoutsakis M,Savaidis A. FE simulation of vehicle leaf spring behavior under driving manoeuvres [J]. International Journal of Structural Integrity,2013, 4 (1): 23-32.

[7]郭孔辉.钢板弹簧刚度计算的主片分析法. 汽车工程,1984(2):22-28.

[8]聂毓琴,孟广伟.材料力学[M].北京：机械工业出版社,2009:155.

[9]周长城,赵雷雷.车辆悬架弹性力学解析计算理论[M].北京: 机械工业出版社,2012.

[10]周长城.汽车平顺性与悬架系统设计[M].北京：机械工业出版社,2011.

[11]林金木,柏伟武.钢板弹簧设计计算[J].汽车工程,1995,17(3):169-176.

[12]Wu W J, Zhu L M, Xiang Y， et al.Novel method for equivalent stiffness and Coulomb’s damping ratio analyses of leaf spring [J]. Journal of Mechanical Science and Technology 2012, 26 (11):3 533-3 538.

(编辑：郝秀清)

Study on the stress and allowable thickness of overlapping part for the leaf spring

SONG Qun， ZHOU Chang-cheng， Pan Li-jun

(School of Transportation and Vehicle Engineering， Shandong University of Technology, Zibo 255049, China)

Abstract:To meet the split design and CAD development for leaf spring, firstly, we found mathematical formula of stress for the overlapping part based on the study of equivalent thickness of the overlapping portion, and according to the relationship between the deformation, thickness and load. Secondly, we proposed mathematical formula of the allowable thickness according to the maximum stress less than allowable stress. Finally, we calculated the maximum stress and the allowable thickness in a practical example and proved them with numerical simulation by ANSYS. The analysis results showed the mathematical method of stress and the allowable thickness for the leaf spring was reliable.

Key words:leaf spring； stress； allowable thickness； equivalent thickness； analytic computation

中图分类号：TH125

文献标志码：A

文章编号：1672-6197(2016)04-0011-04

作者简介：宋群，女，songqunstar@163.com; 通信作者： 周长城，男，greatwall@sdut.edu.cn

基金项目：国家自然科学基金项目(51575325); 山东省自然科学基金项目(ZR2013EEM007); 山东省重点研发计划项目(2015GGX105006)

收稿日期：2015-03-26