一题解说数列不等式恒成立问题
2016-05-04山东张美霞
高中数理化 2016年18期
◇ 山东 张美霞
(作者单位:山东淄博高青县第一中学)
一题解说数列不等式恒成立问题
◇ 山东 张美霞
等差、等比数列是历年高考考查的重点内容之一,通常情况下都会设置1个选择题或填空题和1个解答题.解答题一般设置2个问题,其中第(1)问比较简单,属于基础题;第(2)问有一定的区分度,常与数列求和、不等式证明等知识有密切的联系.其中数列与不等式相联系考查恒成立问题是热点,也往往是学生易丢分的环节.下面举例谈谈这类题的解法.

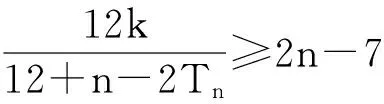


方法1 构造新数列,转化为数列的最大项问题.

当n≥5,cn+1≤cn, {cn}为单调递减数列.
当1≤n<5,cn+1>cn, {cn}为单调递增数列.
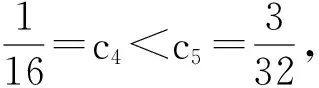
说明 这里对于数列{cn}的单调性的判定除了作差外,我们也可以作商,即
当n≤3时,cn<0;



则x、f′(x)、f(x)变化如表1.

表1

(此处虽然也是构造函数,但是研究的是不含参数的函数.)
从以上解法可以看出分离变量是避开研究含参数问题的关键,构造函数求导时略显麻烦,且由于x是整数,须估值易出错.相比之下构造数列法比较简单,适合广大学生.
总之,适时地构造新数列,利用数列的性质解决问题是解答数列与不等式综合题常用的手段.
(作者单位:山东淄博高青县第一中学)
