热力学函数关系记忆法多媒体教学改革与实践

房慧，张飞鹏，蒋志年

(1.广西民族师范学院物理与电子工程系，广西崇左532200；2.河南城建学院数理学院，河南平顶山467036)

热力学函数关系记忆法多媒体教学改革与实践

房慧1，张飞鹏2，蒋志年1

(1.广西民族师范学院物理与电子工程系，广西崇左532200；2.河南城建学院数理学院，河南平顶山467036)

记忆是与学习紧密相连的人类智能的根本特征之一。针对热力学函数关系在教与学当中的困难，在教学实践中整合图形图像记忆、语音语义记忆和多媒体手段对内能、焓、自由能和吉布斯函数的全微分表达式、偏导数关系式和麦克斯韦关系式展开教学。混合结合记忆的多种感觉通道协作、不同知识点间的链接实现以及课堂交互性设计，可更为有效地提高学生的记忆的效果。

热力学函数；麦克斯韦关系；记忆法

引言

内能、焓、自由能和吉布斯函数的全微分表达式、偏导数关系式和麦克斯韦关系式是热力学[1]103-107、物理化学[2]133-134和地球化学[3]110-112等课程的重要理论基础。采用多元微分学推导方法来进行讲解，虽然逻辑严密、知识脉络清晰、易于理解，但是热力学状态函数间的数学关系式数量多、形式复杂又容易混淆。因此大大增加了初学者运用这些关系式处理具体问题时的难度，难以做到灵活运用。降低了学生学习的兴趣，让学生对学习产生抵触心理，影响了后续课程的教学效果。正因为如此，热力学函数关系式的教学自然成了教与学当中的难点。

记忆是与学习紧密相连的人类智能的根本特征之一。没有形成很好的记忆则智力活动便难以达到一定的广度和深度[4]31-32。为了解决热力学函数关系在教与学当中的困难，在教学实践的过程中产生了众多的、独特的和新颖的记忆方法。

例如，坐标忘记法[1]103-107,[5]74-75,[6]168、矢量图记忆法[2]133-134,[7]58-59,[9]5-8、弧线图记忆法[8]77-80,[10]35-37及其他方便学习的记忆方法[3]110-112,[11]5-7。这些记忆方法从热力学函数关系当中总结出规律，并辅之以简练易记的图形，使学生通过图形图像来更有兴趣地识记、更深入地理解或更方便地运用热力学函数关系式，使教师能更流畅地组织课堂教学、更深入浅出地讲授例题以及更为鲜明地开展再创教学。

经过教学实践，笔者总结出一套结合多媒体教学的记忆方法，在教学活动中受到学生的好评。下面将从中总结出应用图形图像记忆、语音语义记忆和多媒体手段三个方面对该记忆教学方法进行探讨。

一、图形图像记忆

热力学函数关系记忆中主要采用图形图像记忆(见图1)。（一）热力学函数的全微分表达式

热力学函数内能(U)、焓(H)、自由能(F)和吉布斯函数(G)的四个全微分表达式为：

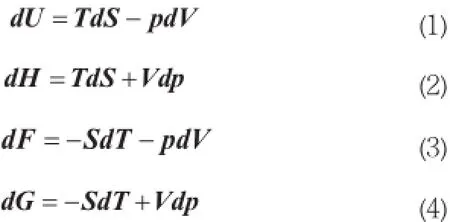
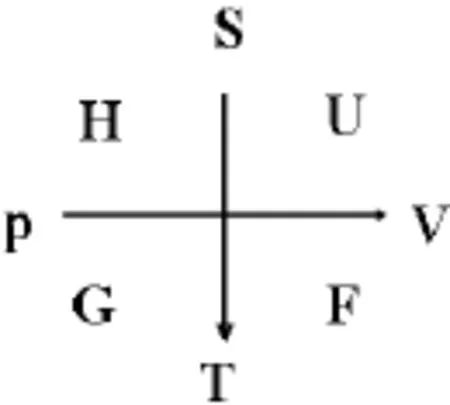
图1 热力学亟数关系记忆总图

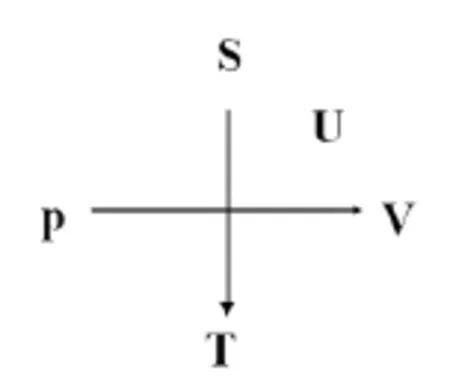
图2 内能(U)全微分表达式记忆图

下面以(1)式为例说明如何利用图1进行热力学函数全微分表达式的记忆(见图2)。

通过第一象限中的热力学函数(U)及两个端量p和V可以得出以下关系式：

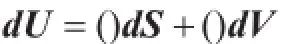
沿着直线分别可以找到括号中的热力学量p和T,此时由V到p为逆箭头方向，而由V到p为顺箭头方向。规定顺箭头方向找到的热力学量为正，则可将-p和T两个量填入括号中即可得热力学内能(U)的全微分表达式(1)。

（二）热力学偏导数关系

通过对(1)～(4)四个热力学函数全微分表达式可以得出八个热力学偏导数关系。将内能U作为熵(S)和体积(V)的函数，则有：

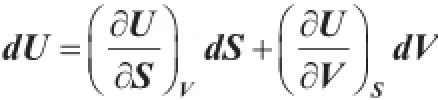
将上式与(1)式进行比较则有

以此类推，由(2)～(4)三个热力学函数全微分表达式可得其余三组共六个热力学偏导数关系式：

下面以热力学偏导数关系式(5)为例，说明如何利用图1进行热力学函数全微分表达式的记忆(见图3)。

从热力学函数内能U起逆时针方向找到第一象限的端量熵S（见图3a），这一步操作相当于/∂∂US。对于内能U，第一象限的两个端量熵S和体积V为其两个独立变量，当内能U对熵S求偏导数时，另一变量体积V不变，于是自然的可以补充下标V，于是可以在这一步操作中写出。接着此时可视纵坐标为等号，并规定顺着箭头方向为正，反之为负。于是可写出与此类推，从图3b中可得到(∂U/∂S)V=-p。

图3 热力学偏导数关系式()5的记忆图

（三）麦克斯韦关系

通过交换(5)～(8)组热力学函数偏导数的次序，可以得到下列四个麦克斯韦关系：

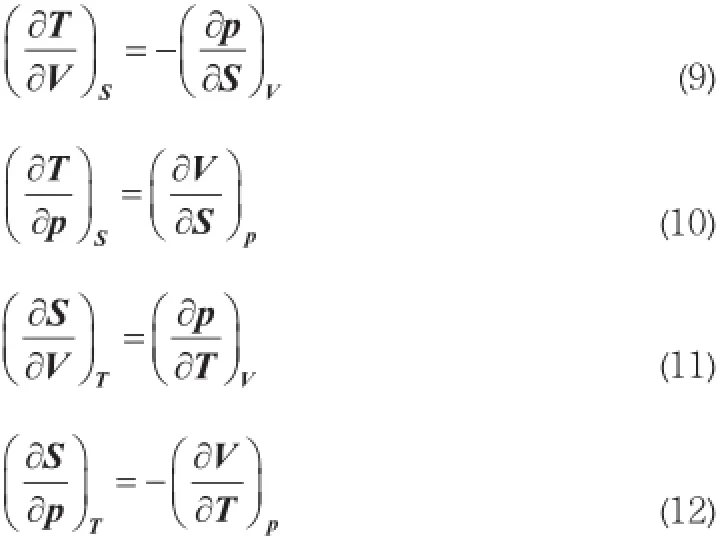
下面以麦克斯韦热力学关系式(9)和(12)为例说明如何利用图1进行热力学函数全微分表达式的记忆(见图4)。

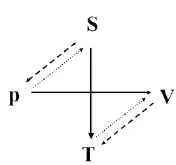
图4 麦克斯韦热力学关系记忆图一对短虚线和点虚线箭头分别对应麦克斯韦关系式()12和(9)

仔细观察不难发现，在麦克斯韦关系式中第二、四象限的端量总是成对出现，而且在麦克斯韦关系式中的偏微分的排列顺序总是顺逆时针结合。于是图4中的一对短虚线可以给出偏导数关系式(∂S/∂p)=(∂V/∂T)。而沿着该箭头所指的顺、逆时针方向得到的下一个端量则作为下标，于是有(∂S/∂p)T=(∂V/∂T)p。另规定第二、四象限得到的麦克斯韦关系式加负号，这样便可以写对麦克斯韦关系式(12)。以此类推，以相似的方法可根据图4中的一对点虚线箭头线写出麦克斯韦关系式(9)。

二、语音语义记忆

为了增强记忆的效果，在教学实践中除了采用图形图像的记忆外还引入了语音语义的记忆。做法是将各记忆图中的逻辑关系编成顺口溜。例如，热力学基本方程记忆法的逻辑关系可用顺口溜“顺者为正逆者负，变量微分看象限端量”来进行描述。而热力学偏导数关系的记忆关系则可以采用“顺者为正逆者负，下标看余端量”来记忆。对麦克斯韦关系的记忆关系利用“对角同向，且为负，下标看下家”这样的顺口溜来帮助记忆。这样的做法一方面能够让学生较为顺利地记住各图中的逻辑关系，并进而能够通过这些逻辑关系写出需要记住的公式；另一方面，在课堂教学中可以让学生通过讨论得出适合个人记忆特点的顺口溜。如此交互性的课堂设计在活跃课堂氛围的同时还可以通过学生的亲身参与加强了记忆，且提高教学效果。

三、多媒体的运用

利用多媒体系统整合图形、图像、影像等信息创设学习情境，能够有效激发学生的学习兴趣、提高学习的积极性[12]71-74。另外，由于视听混合结合记忆的多种感觉通道协合作用以及不同知识点间的链接实现，多媒体的运用能够更为有效地提高学生的记忆的效果[13]62-66,[14]1120-1122。因此，在对热力学函数的记忆教学中要注意采用多媒体的教学手段，将各热力学函数的关系式结合相关的记忆图给学生展示出来。

结语

为了解决热力学函数关系在教与学当中的困难，扩展热力学函数关系式学习的广度和深度。借鉴在教学实践的过程中产生的众多独特和新颖的记忆方法，从热力学函数关系当中抽象中规律性，并辅之以简练易记的图形，使学生通过图形图像的记忆来更有兴趣地识记、更深入地理解或更方便地运用热力学函数关系式。此外，在教学实践中引入语音语义记忆，在让学生记住各图中的逻辑关系的同时还可以通过交互性的课堂设计活跃课堂氛围。另外，结合运用多媒体手段多种感觉通道协作和不同知识点间的链接实现，更为有效地提高了学生的记忆的效果。

[1]张保花,王伟,郭福强.热力学函数及麦氏关系的简便记忆法[J].昌吉学院学报,2010（03）.

[2]王晓晖,孙永安,王晓红.物理化学中热力学函数关系式的教学探讨[J].内蒙古民族大学学报,2012（02）.

[3]陈家玮,杨忠芳,张德会.由“一句话”巧记热力学函数关系式[J].中国地质教育,2005（04）.

[4]边玉芳.遗忘的秘密——艾宾浩斯的记忆遗忘曲线实验[J].中小学心理健康教育,2013（03）.

[5]宋小利,李梅.热力学基本方程、对应系数关系式和麦克斯韦关系式的简捷记忆[J].榆林学院学报,2008（02）.

[6]王树国,袁誉洪,李金林.热力学函数关系式的坐标记忆法[J].广东化工,2010（01）.

[7]陈金文,易平贵,于贤勇.热力学状态函数关系式的记忆法[J].当代教育理论与实践,2011（03）.

[8]吕申壮.热力学关系的图形记忆法[J].大学化学,2011（03）.

[9]吕依颖.简单系统热力学基本方程麦氏关系记忆方法及推广研究[J].枣庄学院学报,2011（05）.

[10]黄艳艳,于忠卫.热力学公式教学中学生记忆的规律性研究[J].高等函授学报(自然科学版),2012（04）.

[11]阿里木江·艾拜都拉,开丽比努尔·艾山,朱玉军.记忆热力学关系式的状态函数正方形和Maxwell正方形[J].北京教育学院学报(自然科学版),2007（02）.

[12]郭晓光.多媒体教学与板书教学的再认识[J].中国教育学刊,2014（02）.

[13]林众,冯瑞琴.多媒体教学中的认知机制[J].教育研究, 2006（7）.

[14]徐家贤,汪彩萍.多媒体要素与记忆规律及情感激励作用关系初探[J].电脑知识与技术,2008（06）.

责任编辑：李凡生

Media Teaching and Practice of the Mnemonics of Thermodynamic Functions

FANG Hui1,ZHANG Fei-peng2,JIANG Zhi-nian1
(1.Department of Physics and Electronic Engineering,Guangxi Normal University for Nationalities,Chongzuo,532200; 2.Institute of Mathematics and Physics,Henan University of Urban Construction,Pingdingshan，467036)

Memory is a fundamental characteristic of human intelligence which also is closely associated with learning.This investigation probes into the difficulties in the learning and teaching among the thermodynamic functions.The teaching practice is carried around the total differential expression,partial derivative equations and Maxwell’s equations of the internal energy,enthalpy, free energy and Gibbs function.The instruction procedure integrates the graphnics memory image,voice semantic memory and multimedia tools.The students’memory effect is improved more effectively by the synergies combination of a variety of sensory channels,the implementatins of the links between different knowledge points and the classroom interaction design.

Thermodynamic functions,Maxwell ralations,Mnemonics

G642

A

1674-8891（2016）03-0050-03

2015-11-23

2014年广西高等教育教学改革工程项目(编号：2014JGB249)；2014年广西高等教育教学改革工程项目(编号：2014JGA245)；高等学校计算物理课程教学研究项目（编号：JZW-14-JW-03）。

房慧(1980—)，男，广西桂林人，广西民族师范学院物理与电子工程系副教授，博士，研究方向：计算材料物理与大学物理教学。