广义mKdV方程的精确解研究
2016-05-03张红伟张强黄英
张红伟,张强,黄英
(1湖南科技大学建筑与规划学院,湖南湘潭411100;2楚雄师范学院数学与统计学院,云南楚雄675000)
广义mKdV方程的精确解研究
张红伟1,2,张强2,黄英2
(1湖南科技大学建筑与规划学院,湖南湘潭411100;2楚雄师范学院数学与统计学院,云南楚雄675000)
modified Korteweg-de Vries(mKdV)方程是一个精典的孤子方程。利用行波变换法把广义mKdV方程转化为常微分后,再利用降阶法和初等积分法求出了广义mKdV方程的一系列的精确行波解。
广义mKdV方程;精确解;行波变换法;降阶法
引言
广义modified Korteweg-de Vries(mKdV)方程
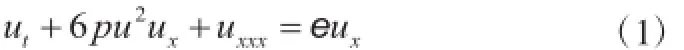
具有丰富的物理背景,其中,为任意常数。当时,方程(1)成了经典的mKdV方程,它可作为非调和晶格中描述等离子和声子多重作用的孤立子模型[1],而当是一个充分小的正数时,方程(1)就变成了扰动mKdV方程,它主要出现在准一维固体的研究中,用于描述原子链和液晶流体力学[2]。特别地,作变换之后,方程(1)被变成了KdV-mKdV组合方程

该方程是等离子体物理和固体物理中的重要模型[1]。一般而言,p=1时,称

为“好的”广义mKdV方程,p=-1时,称
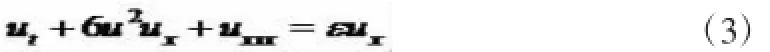
为“坏的”广义mKdV方程。
mKdV方程是一个精典的孤子方程,有关它的精确解有很多学者[3]-[9]研究,但有关扰动mKdV方程和的研究结果并不多见[10]。所以,有必要对方程(1)的行波解进行研究。
一、“好的”广义mKdV方程的解

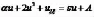
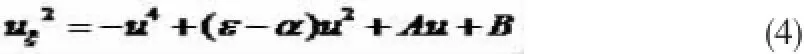
其中,A、B为积分常数。接下来,只需要对常微分方程(4)进行求解,就可以找到方程(2)的特解。
把方程(4)变为

若A=B=0,则用分离变量法可以求解方程(5),从而得到方程(2)的钟状孤立波解
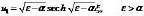
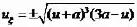
求解之后得到一个有理解
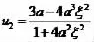
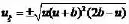
从而得到方程(2)的周期解


利用椭圆积分求解(6)式可得另外两个特殊的周期解
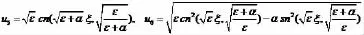
在u1-u5中,ε可以等于零,当ε=0时,这些解就是经典mKdV方程的行波解,但u6在中,ε不能等于零,说明只能是广义mKdV方程(2)的解。此外,后面四种类型的解在相关研究[11]-[16]中极少甚至没有出现过。
二、“坏的”广义mKdV方程的解
经过相同的行波变换和降阶处理后,方程(3)变为

和钟状孤立波解

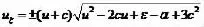
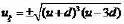
求解之后得到一个有理解
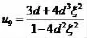

解之得下列周期解

和
在u1-u9以及u12中,ε可以等于零,但u10-u11在中,ε不能等于零,说明典型的mKdV方程不具有形如u10-u11的解,它们只能是广义mKdV方程(2)的解。
[1]李志斌.非线性数学物理方程的行波解[M].北京:科学出版社,2006.
[2]ABLOWITZMJ,CLARKSONPA.Solitons,Nonlinear EvolutionsandInverseScattering[M].Cambridge:Cambridge University Press,1991.
[3]陈登远.孤子引论[M].北京:科学出版社,2006.
[4]黄英,杨波,马祖彦.MKdV方程的新精确孤立波解[J].河南城建学院学报,(2010)(1).
[5]HUANG Y,MA Y,LI B R.Skill application of the theory: new solitary wave solutions and periodic solutions of the modified KdV equation[J].International journal of Functional Analysis,Operator Theory and Applications,2011(01).
[6]WADATI M.The modified Korteweg-de Vries equation[J]. Phys Soc,1972(32).
[7]YANG Z Y,JIANG T.Application of Bifurcation method for gengralized MKdV equation[J].Jouranl of Yuannan University,2002(01).
[8]套格图桑,斯仁道尔吉.MKdV方程和mKP方程的新精确孤立波解[J].高校应用数学学报A辑,2007(1).
[9]HIROTA R.Exact solution of the modified Korteweg-de Vries equation formultiple collisions of solitons[J]. Phys Soc,1972(33).
[10]JIAO X Y,ZHENG Y,WU B.Approximate homotopysymmetry and infiniteseries solutions to the perturbed mKdV equation[J].Applied Mathematics and Computation,2012(218).
[11]WAZWAZAM.Multiple-solitonsolutionsofthe perturbed KdV equation Communications in Nonlinear Science and Numerical Simulation[J].2010(15).
[12]ZARMI Y.From single-to multiple-soliton solutions oftheperturbedKdVequation[J].PhysicaD: Nonlinear Phenomena,2008(237).
[13]VEKSLER A,ZARMI Y.Freedom in the expansion and obstaclestointegrabilityinmultiplesoliton solutions of the perturbed KdV equation[J].Physica D:Nonlinear Phenomena,2006(217).
[14]JIAO X Y,ZHANG H Q.An extended method and its applicationtoWhitham-Kaupequationand two-dimensional perturbed KdV equation[J].Applied Mathematics and Computation,2006(172).
[15]YU J,ZHANG W J,GAO X M.Dynamical behavior in the perturbed compound KdV-Burgers equation[J].Chaos, Solitons and Fractals,2007(33).
[16]GU C H,HU H S,ZHOU,Z X.Darboux Transformation In Soliton Theory And Its Applications On Geometry[J]. Shanghai Scientific and Technical Publishers,2005.
责任编辑:李凡生
Study on the Exact Solutions to the Generalized mKdV Equation
ZHANG Hong-wei,ZHANG Qiang,HUANG Ying (1.Hunan University of Science and Technology,Hunan Xiangtan,411100;2.Chuxiong Normal University,Yunnan Chuxiong,675000)
In the paper,the modified Korteweg-de Vries(mKdV)equation is reduced to an ordinary equation by means of the method of travelling transformation,then the methods of reduction order and elementary integral are used for solving a series of exact solutions to the mKdV equation.
generalized mKdV equation,exact solution,travelling transformation method,reduction order method
0175.2
A
1674-8891(2016)03-0004-03
2015-11-23
云南省教育厅资助项目(编号:2012Y130);国家自然科学基金资助项目(编号:11261001)。
张红伟(1986—),男,河南项城市人,湖南科技大学建筑与规划学院硕士研究生,研究方向:非线性发展方程;黄英(1973—),女,云南大姚人,云南省楚雄师范学院数学与统计学院教授,主要从事非线性发展方程和无穷维动力系统的研究。
