多工序生产过程中时间组织问题的图解优化模型

李柏敏

（广西民族师范学院经济与管理系，广西崇左532200）

多工序生产过程中时间组织问题的图解优化模型

李柏敏

（广西民族师范学院经济与管理系，广西崇左532200）

产品在加工过程中往往无法在一台设备或工序上完成，在不同设备或工序之间移动的时候涉及移动方式的选择问题。流行的加工方式分别为顺序移动、平行移动和平行顺序移动等三种，各自的加工总时间的计算公式各不相同。研究并分析这些方法的不足，提出通过图解法求总生产周期、各工序生产周期、开始时间矩阵和结束时间矩阵等有用信息。通过实例计算证明PT图解法的可行性和有效性，并给出了便于用计算机实现的程序伪代码，为处理大批量数据提供了切实可行的方法。

多工序生产过程；移动方式；时间组织；PT图解法

随着生产加工过程中自动化程度不断提高，管理者对生产效率有着越来越高的追求，流水线作业应运而生。在多工序生产过程中，一批产品按照一定的工艺顺序在不同的机器或车间进行加工并最终形成产成品，但是由于产品在不同工序上加工所耗费的时间不一样，在实际生产中实现产品连续加工的“无缝对接”具有一定的难度，甚至是不可能实现的。考虑到产品的搬运次数、搬运距离、加工时间等因素，便出现了几种不同的产品在多个工序间移动方式的问题，当下最为流行的加工方式分别为顺序移动、平行移动和平行顺序移动等三种。

一、工序移动方式概述

产品在加工过程中往往无法在一台设备或工序上完成，因此在不同设备或工序之间移动的时候就涉及移动方式的选择问题。单件产品的移动不存在方式的选择，但是实际生产过程中，产品的加工制造以批量化方式为主。而每件产品的移动，是以独立方式移动还是多个产品合并为一个整体的批量移动，不仅会对加工设备的工作状态（连续加工或者是间断加工）产生影响，也会对总体的生产加工时间造成差异。除此之外，针对不同的生产加工方式，每道工序该何时加工、何时中断及何时结束也是在决策者在制定具体生产计划时需要考虑的问题。下面将简要介绍下目前已有的三种移动方式，为下文的图解法奠定基础。

在文中，所涉及的产品加工中，基于如下基本假设：1.产品对设备具有独占性，在某一特定时间，只能有一件产品在特定设备上进行加工操作；2.产品具有不可分割性，在某一特定时间，只能有一台设备对某种产品进行加工；3.同一产品在不同设备上的加工顺序固定不变，即必须按照统一的顺序从第一道工序逐渐转移到最后一道工序，最后完成产品加工；4.不考虑产品在不同工序间移动所需要的时间。

（一）顺序移动方式

顺序移动方式是指产品作为一个整体在不同设备之间进行移动，某产品完成工序A后，等候其他产品，待所有产品均完成A工序，再统一移动到下一道工序B继续加工。该方式下的总加工时间的计算公式为[1]

(二)平行移动方式

平行移动方式是指产品以独立方式移动，每件产品在加工过程中保持运动的独立性，不必等候其他产品，采用“随到随走”的形式，此时各产品将在各道工序上同时加工，处于平行方式。此时对应的总加工时间计算公式为[1]

(三)平行顺序移动方式

平行顺序移动方式是上述两种方式的结合，它既体现出产品在各台设备上加工的连续性，同时又尽可能使得每件产品能够在完成上一道工序后尽快进行转移以继续下一步加工。该移动方式对应的总加工时间的计算公式为[1]

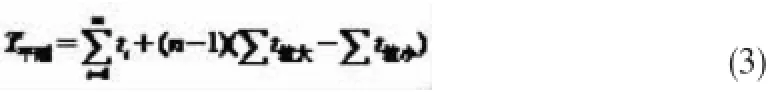
上述(1)~(3)式中，n为产品的批量，m为加工工序的道数，ti为第i道工序的单件工时，t最长为各道工序中，单件工时最长的那道工序的单件工时，即t最长=max(ti)，t较长为比相邻工序单件工时均大的工序的单件工时，即，t较小为比相邻工序单件工时均小的工序的单件工时，即，针对第一道工序和最后一道工序，可假定m0=tm+1=0存在，便仍可采用上述判断和的方法。

例1：假定现有一批零件，共计4件，零件完成全部加工过程需要5道工序，各道工序的加工停留时间（分钟）依次为10、5、20、10、5。则根据上述公式，可算得三种移动方式下，将4件产品全部生产出来所需要的时间为：

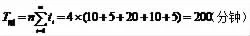
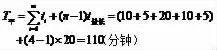
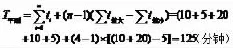
应用上述公式，能够计算出工序加工的总时间，但是不能得出具体的生产过程执行情况，比如第件产品在第j道工序上的加工开始时间，加工结束时间，车间（工序j）机器应何时开机、何时停机，何时处于工作状态、何时处于暂停等待状态等。而这些信息对于安排生产加工至关重要，若不能事先做好安排，将导致具体执行时手忙脚乱，无法按照预定的目标完成生产任务。

目前已有一些学者针对这一问题进行了一些研究，例如学者段渊[2]33-36提出了两道工序的加工顺序的新解法，但其产品各不相同，在不同设备上的耗时也不相同，主要是对约翰逊方法的眼神和扩展；文献[3]68-70中，考虑了运输时间，然后将(1)~ (3)式的形式复杂化了，但是并没有解决求解结果单一且不易理解的问题，另有文献[4]297对这一问题有所涉及，但只是将生产周期的求解公式加以应用，并无创新，此外，文献[5][6]也对相关问题进行了讨论，但是均存在一些不足之处。因此，此文中笔者将采用一种新的工序——时间图（Process-Time图，简称PT图）来解决这一问题，建立较为完备的模型，使得系统输入基本信息之后，能够得到对管理者和产品加工工人都有用的各类信息，以更好地辅助生产。

二、生产过程时间组织的图解法

为方便表述，首先约定如下符号：n为产品的批量，m为加工工序的道数，ti为第i道工序的单件工时（i=1,2,……m），tsij为第j件产品在第道工序上的开始时间，teij为第j件产品在第i道工序上的结束时间（显然）teij=tsij+ti，T为全部产品完成全部工序的总时间，即生产周期。在PT图中，以“■”标记工序的开始（包括暂停后的再次开机），以“▲”标记工序的结束（包括机器的暂停）。

采用PT图求解的一般步骤为：

Step1：绘制一张PT图，m+1画出条水平平行线，第一条线用于标注时间，从时刻0开始，第二行至最后一行，每条水平线代表一道工序，可在最左端予以标注工序编号和单件工时；对于时间刻度的标注，可先计算所有ti的最大公约数t0，然后可以此作为时间分隔的基本单位。

Step2：令i=1，从工序1开始，在时刻0对应ts11=1的位置标记“■”，此位置对应ts11=0，表示产品1在工序1上开始加工的时刻，然后在te11=0+ti的位置标记数字“1”，表示第1个产品在te11时刻完成了第一道工序，以此类推，在te1j=0+jt1= te1j-1+t的位置标记数字“j”（j=1,2,...,n），表示第j个产品完成了第1道工序；并在第n个产品完成的位置同时标记“▲”以表示工序1结束。

Step3：令i=2，转入工序i，产品在工序i上的开始与结束时间依赖于移动方式，具体可分为如下三种情况：

1.顺序移动方式下：在te1j=te(i-1).n的位置标记“■”，代表工序的开始，然后依次在te1j=tsi1+jti=tei.j-1+ti的位置标记数字“j”（j=1,2,...,n），表示第j个产品完成了第i道工序；并在第n个产品完成teinj=tsi1+nti的位置同时标记“▲”以表示工序结束。

2.平行移动方式下：首先比较ti与ti-1的大小，若ti≥ti-1，则其标记过程为：在te1j=te(i-1).1的位置标记“■”，然后依次在te1j= tsi1+jti=tei.j-1+ti的位置标记数字“j”（j=1,2,...,n）；并在teinj=tsi1+nti位置同时标记“▲”以表示工序i结束。若ti＜ti-1，则其标记过程为：在所有te1j=te(i-1).j的位置标记“■”（j=1,2,...,n），然后依次在te1j=tsi1+ti的位置标记数字“j”（j=1,2,...,n）；同时标记“▲”。

3.平行顺序移动方式下：首先比较ti与ti-1的大小，若ti≥ti-1，则其标记过程为：在te1j=te(i-1).1的位置标记“■”，然后依次在te1j=tsi1+jti=tei.j-1+ti的位置标记数字“j”（j=1,2,...,n）；并在teinj= tsi1+nti位置同时标记“▲”以表示工序i结束。若ti＜ti-1，则其标记过程为：在tsi1=te(i-1)..(n-1)-(n-1)ti的位置标记“■”，然后依次在te1j=tsi1+jti=tei.j-1+ti的位置标记数字“j”（j=1,2,...,n）；在tem=tsi1+ nti位置同时标记“▲”以表示工序i结束。

Step4：若i＜m，则令i=i+1，更新i值后转入Step3重复执行；若i=m，则执行过程结束，可输出总加工时间T=temn，各工序上各产品的生产开始时间矩阵TS=（tsij）mxn，生产结束时间矩阵TE=（teij）mxn等信息。

三、实例应用及计算机解法

例2：依照上述方法，例1中三种移动方法分别对应的加工时间图如下：

注1：图1中，由于时间轴较长，限于篇幅，对60-140之间的刻度进行了适当放大，每个刻度代表10分钟。

注2：各PT图中，左侧ti表示工序及单件工时，顶行数轴代表时间，从0时刻起，■表示机器开始运转，▲表示机器停止运转。

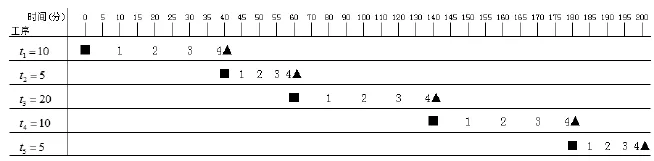
图1 顺序移动方式的PT图

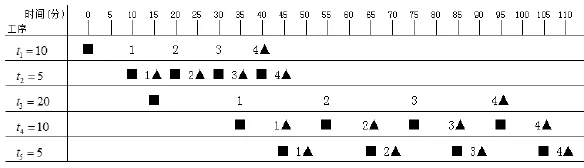
图2 平行移动方式的PT图

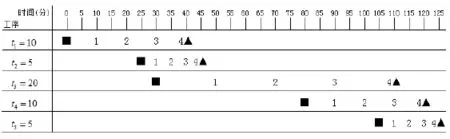
图3 平行顺序移动方式的PT图

从图1至图3中，可以清楚地看到每种移动方式对应的加工总时间T，各工序上各产品的生产开始时间矩阵TS，生产结束时间矩阵TE。即T顺=200（分钟），T顺=110（分钟），T顺= 125（分钟）。

从计算结果，可以得出以下结论：

1.T顺＞T平顺≥T平，即顺序移动方式耗时最长，但其操作相对简单，产品搬运次数最少，平行移动方式耗时最短，但是不同产品在同一道工序上加工时存在间断现象，停机次数更为频繁，而平行顺序移动方式由于结合了二者的优点，因此其停机次数介于二者之间。

2.TEi.=TSi.+(ti)1xn，即结束时间矩阵的各行等于开始时间矩阵对应行加上该工序的单位工时。

3.在顺序移动方式中，有tsi.j+1=teij（j=1,2,...,n-1），第j+1个产品在工序i上的开始加工时间等于第j个产品在工序i上的结束加工时间。

4.若以TS（i：）表示矩阵的第i行，则有TS顺（1：）=TS平（1：）=TS平顺（1：），TE顺（1：）=TE平（1：）=TE平顺（1：）。即，对于三种不同的移动方式而言，所有产品在第一道工序上的时间组织不存在差异。

5.若以TS（i，j）表示矩阵的第i行第j列元素，则有TS（i，1）表示各工序的开始时间，TS（i，n）表示各工序的结束时间。若以TI表示各工序的生产周期，即从第一个产品开始加工到最后一个产品结束加工的时间，则有TI=TE（i，n）-TS（i，1），在例2中，则有TI顺=（40，20，80，40，20）T，TI平=（40，35，80，70，65）T，TI平顺=（40，20，80，40，25）T。通过比较可以看出TI平顺=TI平顺≤TI平，即平行顺序移动通过合理选择工序起点，避免了加工过程中的暂停，其各个工序的生产周期与顺序移动方式是一致的，这种方式将设备的空余时间集中利用，可以发挥更大的作用。而平行移动方式下，由于单件工时存在差别，在“急功近利”的指导思想下，会导致单价工时小的工序存在多次的暂停，把这一时间计入工序的生产周期，必将导致工序生产周期的增加。

应用图解法对不同移动方式的加工安排执行过程进行了求解，但是当工序和产品都增加的时候，采用这一方法则存在效率不高的问题。此时，可以按照上述步骤，将求解过程编成可执行程序，借助计算机的高效和快速计算能力进行求解。下文以较为复杂的平行顺序移动方式为例，给出其计算机解法的伪代码如下：

%-----------------------------

初始化各ti值及m，n

i=1;ts11=0;

Forj=1:n

ts1j=ts11=（j-1）t1

te1j=ts11+jt1

End for

Fori=2:m

Ifti≥ti-1

tsij=te（i-1）1

Else

tsij=te（i-1）.（n-1）-(n-1)t1;

End if

For j=1∶n

tsij=tsij+(j-1)t1teij=tsi1+jti;

End for

End for

T=temn;

For i=1:m

将每个tsi1对应的位置标记■;

将每个teim对应的位置标记▲;

For j=1∶n

将每个teij对应的位置标记数字“j”;

End for

End for

输出PT图;

输出生产周期;

输出生产开始时间矩阵TS=（tsij）mxn;

输出生产结束时间矩阵TE=（teij）mxn.

%-----------------------------

结语

针对现有方法求解不同移动方式时仅能求解加工总时间的问题，提出了求解这类问题的PT图解法，并给出了相应的计算机解法，将该方法应用到生产过程的时间组织问题中，不仅能求解加工总时间，而且可以求解每个产品在各道工序上的开始时间、结束时间，也可求得各工序上机器的开机时间和停机时间，为求解这类问题提供了新的方法，方法简单可行，能为管理者合理安排生产提供参考，为一线工人有效贯彻执行生产计划提供指导，具有一定的现实意义。

[1]张仁俠.生产与作业管理[M].北京：中国财政经济出版社，2007.

[2]段渊.基于两道工序加工顺序安排的解法创新[J].湖南文理学院学报（自然科学版），2011(03).

[3]孔继利.考虑运输时间的生产过程时间组织问题研究[J].物流工程与管理，2010(04).

[4]唐国银.浅谈生产过程中时间组织移动方式的应用[J].中小企业管理与科技，2009(16).

[5]赵启兰.企业物流管理[M].北京：机械工业出版社，2005.

[6]齐二石，朱秀文，何桢.生产与运作管理教程[M].北京：清华大学出版社，2006.

责任编辑：李凡生

Graphic Method of the Multi-Step Production Process of Time Organizational Issues

LI Bo-min
(Department of Economic and Management,Guangxi Normal University for Nationalities,Chongzuo,532200)

This paper begins with a brief introduction to the concept of moving the processed products in the process,and gives the current formula to calculate the total processing time.By analyzing the deficiencies of existing methods,a new graphical method is given,the total production cycle can be determined by the graphic method,the production cycle of each step,the start time matrix and end time matrix and more other useful information can be calculated at the same time,which has some significance in the decision-making process.Finally,an example shows the feasibility and effectiveness of the proposed method,and the pseudo-code easy to use computer-implemented program is given,which provides a practical method to handle large amounts of data.

multi-step production process,move method,time organization,PT graphical method

F273

A

1674-8891（2016）03-0024-04

2016-04-08

李柏敏（1982—），男，瑶族，广西桂平人，广西民族师范学院经济与管理系讲师，研究方向：边境物流、企业物流。