一类非线性变号二阶边值问题正解的存在性

王静

（兰州文理学院师范学院，甘肃兰州730000）

一类非线性变号二阶边值问题正解的存在性

王静

（兰州文理学院师范学院，甘肃兰州730000）

考虑一类非线性变号二阶三点边值问题运用锥上的Guo-Krasnoselskii’s不动点定理研究一类非线性变号二阶三点边值问题至少存在两个正解

非线性；边值问题；正解

微分方程边值问题在应用数学与物理领域中都有十分广泛的应用，在化学和工程领域中应用更为普遍。近年来，二阶边值问题研究取得了一些非常好的结果，如文献[1]1417-1427，[2]458-466，[3]443-452，[4]2628-2638，[5]2756-2766，[6]344-350，[7]1-10，[8]32-35。在文献[2]中，Li和Su运用不动点指数定理研究了一类变号二阶三点边值问题

在此文中，笔者讨论一类非线性变号三点边值问题

两个正解的存在性，其中

为便于讨论，做记号如下：

证明过程需要Guo-Krasnosel’skii不动点定理[9]。

定理1设E是Banach空间，锥K⊂E，Ω1和Ω2是E中有界开集，0∈Ω1，Ω1⊂Ω2，A:K∩（Ω2Ω1）→K全连续，若A满足：

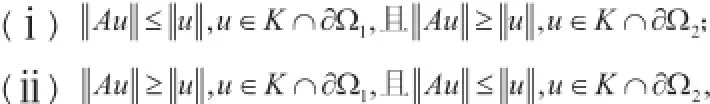
则A在K∩（Ω2Ω1）中必存在不动点。

定理2.设(A1)-(A3)成立。若下面条件成立，

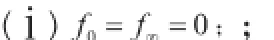
则边值问题（1）至少存在u1u2两个正解，且有

一、预备引理

引理1.若y∈C[0，1]则二阶边值问题

有唯一解

其中，格林函数G(t，s)是：

引理2.格林函数G(t，s)满足下列性质：

其中△如（2）所示。

可知P是E中的锥。

引理3.假设u∈P，那么u(t)有下列性质：其中

证明：(ⅰ)由u∈P，在[0,η]上u是凹函数，在[η,1]上u是凸函数，由于u（0）=αu'（0），u（1）=βu（η），则有

对于t∈[η,1]，有

对于，得

证明：对，可得

由f是非减函数，则对，有

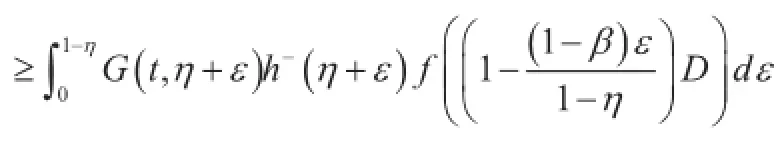
引理5.设(A1)，(A2)，(A3)成立.则算子是全连续的。

证明：很容易证得，再由于是非减函数，据引理3中的(ⅰ)和引理4可知

从而

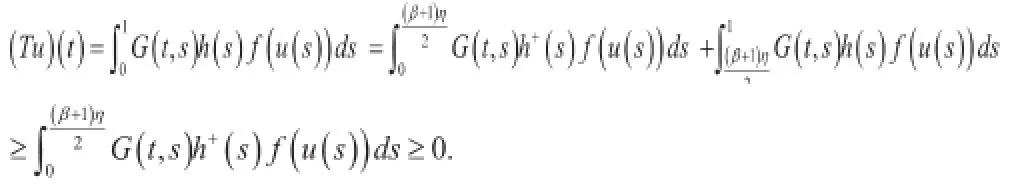
据

可由Arzela-Ascoli定理证明T是全连续算子。

二、定理的证明

因此

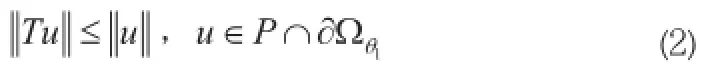
分类讨论：

Case1，若f（u）是有界函数，那么∃N＞0，使f（u）≤N设并且可知

Case2，若f（u）是无界函数。设u≤θ2，可知f（u）≤f（θ2）。并且对于u∈P，有可知。从而可得。假设，综上可知

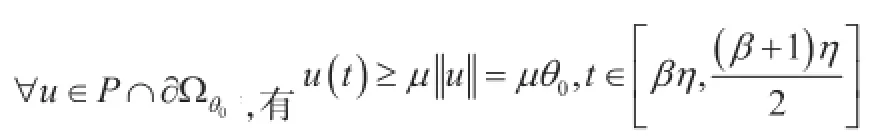
而θ1＜θ2＜θ3，由(2)、(3)、(4)式及定理1可知，T存在两个不动点

结论：边值问题(1)有两个正解u1，u2且

[1]ATICIFM，CABADAA.Existenceanduniqueness results for discrete second-order periodic boundary valueproblems[J].Computers&Mathematicswith Applications，2003，45.

[2]LI C Y，SU Y J.Existence of sign-changing solution for three-point boundary value problems[J].Chin Quart J of Math，2012，27.

[3]BAI D L，FENG H Y.Eigenvalue for a singular second order three-point boundary value problem[J].Appl Math Comp,2012，38

[4]KONGLJ.Secondordersingularboundaryvalue problemswithintegralboundaryconditions[J]. Nonlinear Analysis，2010，72.

[5]LIUB，LIUL，WUY.Positivesolutionsforsingular second order three-point boundary value problems[J]. Nonlinear Analysis，2007，66.

[6]SUN B，YANG A，GE W.Successive iteration and positive solutionsforsomesecond-orderthreepoint p-laplacian boundary value problems[J].Mathematical and Computer Modelling，2009，50.

[7]XI S，JIA M，JI H.Multiple nonnegative solutions for second-orderboundaryvalueproblemswith sign-changingnonlinearities[J].Electron.J. Differential Equations，2009，66.

[8]YAO Q.An existence theorem of positive solution f or a superlinear semipositone second-order three-poin tBVP[J].Mathematical Study，2002，35.

[9]GUOD，LAKSHMIKANTHAMV.NonlinearProblemsin Abstract Cones[M].New York:Academic Press，1988.

责任编辑：李凡生

The Existence of Positive Solutions to Nonlinear Second Order Boundary Value Problem with Change of Sign

WANG Jing
(Normal School,Lanzhou University of Arts and Science,Lanzhou,730000)

This paper studies the following nonlinear second order three-point boundary value problemexistence of at least two positive solutions is studied by using the Guo-Krasnoselskii's fixed-point theorem in cones.

nonlinear,change of sign,boundary value problem,positive solution

O175

A

1674-8891（2016）03-0001-03

2015-12-30

甘肃省教育厅科研项目（编号：1015B-02）；兰州文理学院科研项目（编号：2015GSP07）

王静（1981-），女，山东莱州人，兰州文理学院副教授，主要从事微分方程的研究。