基于广义状态空间平均的独立电力系统建模方法
2016-05-03杨占刚吴惠东屈俊超车延博
杨占刚, 吴惠东, 屈俊超, 车延博
(1. 中国民航大学电子信息与自动化学院, 天津 300300; 2. 天津大学智能电网教育部重点实验室, 天津 300072)
基于广义状态空间平均的独立电力系统建模方法
杨占刚1, 吴惠东1, 屈俊超1, 车延博2
(1. 中国民航大学电子信息与自动化学院, 天津 300300; 2. 天津大学智能电网教育部重点实验室, 天津 300072)
针对由各类电力电子装置构成的独立电力系统应用日趋普及的现状,为对不同运行工况下独立电力系统进行描述,提出一种基于广义状态空间平均的独立电力系统建模方法。通过将独立电力系统时变非线性微分方程状态变量用傅里叶系数描述,得到独立电力系统的广义状态空间平均模型;依据独立电力系统的不同运行工况,分析其不同时间尺度的动态特性,并通过傅里叶系数的增减实现微电网的广义状态空间平均模型化简。该建模方法能甄别独立电力系统的运行工况及动态特性,在系统分析和设计中可代替时域模型,在稳态时可简化为状态空间平均模型。仿真结果表明该模型具有良好的精度和快速的分析能力,适用于独立电力系统的稳态、暂态分析领域。
独立电力系统; 广义状态空间平均; 动态特性; 傅里叶系数
1 引言
随着电力电子技术的发展,电力电子装置在国民经济和国防建设的诸多领域应用越来越广泛,尤其是由电力电子装置构成的各种独立电力系统,如可联网、孤岛两种模式运行的微电网,各载运工具如飞机、船舰、航天器的电力系统等应用日趋普及[1,2]。一个典型的独立电力系统包括电源系统、配电系统、用电设备三部分。独立电力系统由于含有大量的电力电子变流装置,是一个高维复杂非线性系统,其安全稳定运行不仅受到常规电力元件动态特性影响,而且与电力电子装置的动态特性密切相关,并且独立电力系统的应用领域、运行环境千差万别,因此建立反映其动态特性的数学模型至关重要。目前,独立电力系统的建模主要包括时域仿真法与解析建模法两大类。
时域仿真法,即通过描述各元件和全系统暂态过程的微分方程建立的模型,可以精确反映系统中快速电磁过程,能够给出大扰动、非线性、时变系统的精确响应,对事故现场进行再现,是一种古老的方法。在过去很长时间中,时域仿真法被认为是判断电力系统运行状态最准确、最可靠的方法,在各类研究中被广泛应用[3]。由于研究的需要,至今世界各国已先后研制和完善了多种时域仿真软件,如美国邦纳维尔电力局的主要用于电磁暂态仿真的EMTP(包括微机版ATP-EMTP)、美国电力研究协会的用于中长期稳定性研究的ETMSP和配套的SSSP、美国PTI公司的PSS/E、法国国家电力公司的EUROSTAG、ABB公司的SIMPOW和中国电力科学院的综合稳定程序(PSASP)等。时域仿真法的优点是精确度高,可以得到响应的完整波形,适用范围广。具体到独立电力系统时域仿真领域,其重点关注于模型的降阶与仿真速度的提高,以实现对独立电力系统的实时仿真[4]。文献[5]针对独立电力系统提出了一种在传统奇异摄动模型降阶方法基础上的模型降阶方法,通过将原系统稳定裕度指标在奇异摄动参数处进行高阶泰勒级数展开,给出定量预测降阶系统稳定裕度指标的表达式,从而实现对系统模型降阶。文献[6]以Krylov子空间理论与矩匹配原理为基础,提出了一种面向时域仿真的大规模电力系统网络降维化简方法,为时域仿真的快速性问题提出了一种新的解决思路。另外,文献[7,8]通过并行计算、自动微分等技术提高数值仿真的运算效率。在独立电力系统的稳定性分析中,时域仿真方法多用来作为其他稳定性分析结论的辅助验证工具。文献[9]利用时域仿真技术,对独立电力系统中特定运行条件下的暂稳态行为进行验证,可实现对不同架构独立电力系统的参数校正测试。文献[10]则利用时域仿真技术,对独立电力系统的基波及谐波进行实时估计,进而为独立电力系统中的有源及无源滤波器的设计提供参考。但总体来说,时域仿真方法缺点是物理概念不清晰,不能够从根本上揭示系统的工作机理,对设计的指导意义不大,也无法为控制方案的设计提供理论指导。
解析建模法,是指利用解析表达式表示系统特性的建模方法,为此需要作某些近似假定,以简化分析。其中最具代表性的是Middlebrook 提出的状态空间平均法,它从系统不同拓扑下的状态方程出发,经过平均、小信号扰动和线性化处理步骤,得到表征系统稳态和动态小信号特性的数学模型[11]。文献[12,13]基于该方法,分别对独立电力系统的机电作动器及整流器进行了状态空间建模;文献[14]基于状态空间平均法,建立了独立电力系统中逆变环节的dq模型描述方程,用于独立电力系统的仿真和故障诊断研究;文献[15]建立了以AC/DC为核心,以驱动类负荷为主的独立电力系统状态空间仿真模型并用于系统的小扰动分析。由于状态空间平均法在推导过程中假设状态变量在开关周期每个阶段只有微小变化,只能得到状态变量的周期平均分量的动态方程进行直流稳态分析和动态小信号分析,不能进行纹波分析、大信号分析。为了继续发挥状态空间平均法的优点,文献[16]提出了平均处理过的状态空间平均法建模方法,此法的中心思想是把状态变量划分为快变和慢变状态变量,并对快变状态变量做出某种处理,可成功地分析瞬态过程及纹波,常用于二阶系统的分析,但对于高阶系统,则求解复杂繁琐,推广性有待进一步验证。可以看出,目前独立电力系统的状态空间建模多为在忽略系统动态特性基础上,对独立电力系统中某一特定组成部分,如AC/DC、DC/AC等环节的单独建模分析,考虑不同运行工况动态特性的独立电力系统整体建模研究仍待进一步拓展。
可以看出,能够描述系统内部详细动态过程的时域仿真建模方法相对复杂,仿真速度慢;而相对简单的状态空间建模方法又忽略了系统的动态特性,且不能适用于大扰动分析。因此,如何针对独立电力系统的特点,为独立电力系统建立简单而又比较准确的数学模型,使之既能够适用于大扰动系统的仿真分析,又包含一定的内部动态行为,仍是一个迫切需要研究的课题。
2 独立电力系统动态特性分析
独立电力系统是一个时变非线性系统,既包含同步发电机等具有较大时间常数的旋转设备,也有响应快速的电力电子装置。在系统发生扰动时,既有在微秒级快速变化的电磁暂态过程,也有毫秒级变化的机电暂态过程和以秒级变化的慢动态过程。针对独立电力系统不同层次动态特性,建立反映独立电力系统动态特性的数学模型并以此为基础进行独立电力系统动态分析至关重要。文献[17]针对独立电力系统中的电源拖动装置动态特性对电力系统的影响进行了初步探讨。在独立电力系统中,其动态特性非常复杂,若考虑所有动态特性进行独立电力系统建模,虽保障了模型精度,但是将导致模型复杂程度高及不可预计的计算时间。针对不同的研究目的和应用场合,并不总需要对独立电力系统所有动态特性进行考虑,因此需要在分析独立电力系统动态层次基础上,对一些特定模式下的动态特性加以忽略并适当化简。具体的,独立电力系统动态大致可分为四个层次:①元件级动态,指频率在100kHz以上的动态特性,用来描述元件(如固态开关、电磁作动器等)的高频、电磁暂态、热力学领域等特性;②行为级动态,指频率在100~100kHz的动态特性,用来描述独立电力系统中变换器开关切换、谐波及电磁兼容等特性;③功能级动态,指频率在100Hz以下的动态特性,用来描述系统为完成某项功能,进行的设备启停、负载投切等稳定性方面的动态特性;④结构级动态,指独立电力系统的稳态特性,用于独立电力系统的潮流计算,进行电网容量、结构等方面的设计。
广义状态空间平均模型是介于详细时域模型和简化的状态空间模型之间的一种建模方式[18]。该方法的主要思想是:电路状态变量用时变傅里叶级数展开来近似,电路可以表示成一组以傅里叶级数为状态变量的微分方程,并通过忽略系统状态变量所对应的傅里叶级数中那些不重要的项而对原系统进行简化,傅立叶级数中所选的谐波次数越高,电路状态变量就越接近实际值。图1为独立电力系统的动态特性变化趋势与广义状态空间平均模型的对应特性。
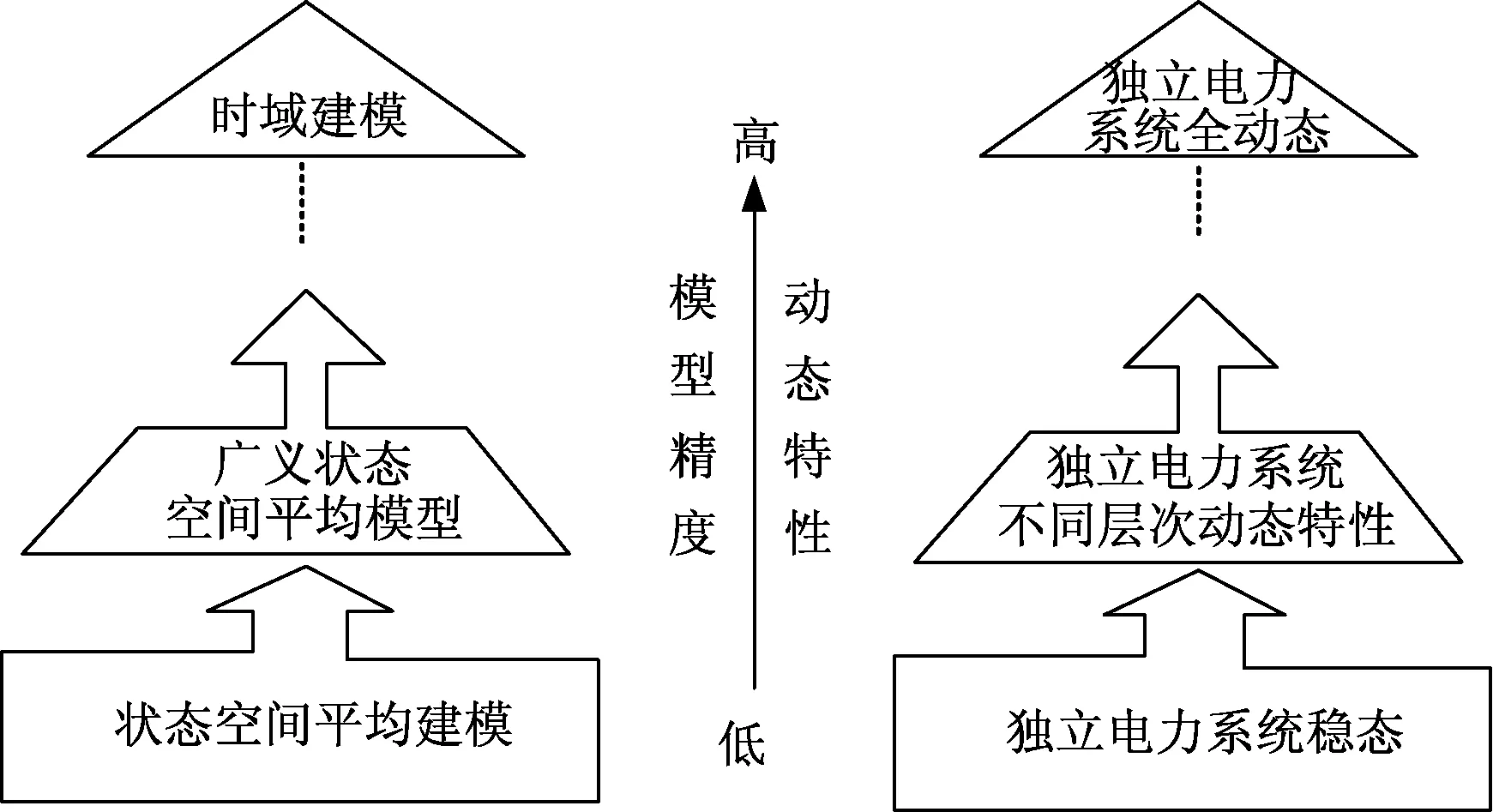
图1 广义状态空间平均模型与独立电力系统动态特性Fig.1 Generalized state space averaging and dynamic characteristics of isolated power system
可以看出,独立电力系统动态特性与广义状态空间平均模型具有相似的变化趋势,随着广义状态空间平均模型阶数的增加,其包含的独立电力系统的动态特性越多,但模型的复杂度也会相应提升。基于此,对不同运行状态下的不同层次的动态特性进行分析,并依据不同应用场合的不同需求,确定傅里叶系数与独立电力系统动态特性具体的对应关系,实现对模型的化简,进而构建出反应不同运行状态下不同动态特性的独立电力系统简化广义状态空间平均模型。
3 独立电力系统广义状态空间平均建模
为实现反映不同尺度时间动态特性的独立电力系统建模,采用广义状态空间平均模型对独立电力系统进行建模,该方法实施步骤如下:
(1)依据独立电力系统结构,建立独立电力系统中电源系统、配电系统、用电设备的时变非线性微分方程,确定独立电力系统时变非线性微分方程的状态变量:

(1)
式中,χ=[x1,x2,…,xn]T为系统状态变量;Ψ为系统状态变量矩阵,为n×n阶矩阵;u=[u1,u2,…,um]T为系统代数变量;Γ为系统代数变量矩阵,为n×m阶矩阵。
(2)依据步骤(1)所确定的独立电力系统时变非线性微分方程的状态变量,对状态变量χ进行傅里叶分解,对任一时变状态变量xi(τ),在任一区间τ∈[t-T,t]中,均能够用时变傅里叶级数表示:
(2)
content_right
(3)
(3)根据得到的傅里叶系数
k=0时:
(4)
k≠0时:
(5)
式中,q为新引入的状态变量矩阵Q中的元素。
(4)对步骤(1)得到的独立电力系统时变非线性微分方程进行k阶傅里叶分解,得到:
(6)
k=0时:
(7)
k≠0时:
(8)
(9)
式中,Re代表对函数取实部;Im代表对函数取虚部。
(5)将步骤(3)得到的状态变量q代入步骤(4)的傅里叶分解后的微分方程,并引入状态变换矩阵M:
k=0时:
(10)
式中,Q0=[q1,q2,…,qn]T;Ψ0=Ψ;Μ0=<Γu>0。
k≠0时:
(11)
式中
Ψk=
则最终的独立电力系统的广义状态空间平均模型可描述如下:
(12)
(6)针对独立电力系统的运行工况,依据独立电力系统设备启停、功能变换、结构切换、稳态设计的功能需求,将独立电力系统动态特性分为四种层次:元件级动态、行为级动态、功能级动态、结构级动态。
(7)依据步骤(6)得到的独立电力系统四种层次的动态特性,合理选择傅里叶分解的阶数N,对独立电力系统的广义状态空间平均模型进行化简,得到四种层次下反映独立电力系统动态特性的简化广义状态空间平均模型。
4 算例分析
为验证提出的基于独立电力系统动态特性的广义状态空间平均建模方法的有效性,本文以某典型独立电力系统中恒电压Buck变换器(如图2所示)为例,进行广义状态空间平均建模。

图2 独立电力系统Buck变换器结构图Fig.2 Schematic of Buck converter in isolated power system
4.1 恒电压Buck变换器广义状态空间平均建模
(1)建立独立电力系统中带恒电压负载输出的Buck变换器时变非线性微分方程如下:
(13)
式中,rv为线路电阻;Lv为线路电感;Iv为电感电流;Cv为输出稳压电容;VCv为电容电压;h(t,Tv)为开关器件占空比;Vdc为输入电压值。确定该Buck变换器的状态变量为Iv、VCv。
(2)确定由步骤(1)得到的时变非线性微分方程的状态变量Iv、VCv,并对该状态变量进行傅里叶分解:
(14)
(15)
式中,
(16)
(17)
(3)根据得到的傅里叶系数
k=0时:
(18)
k≠0时:
(19)
(4)对Buck变换器的微分方程进行k阶傅里叶分解,得到:
k=0时:
(20)
k≠0时:

(21)

(22)
(5)将步骤(3)得到的状态变量q代入步骤(4)的傅里叶分解后的微分方程,并引入状态变换矩阵M:
k=0时:
(23)
式中
Q0=[q1,q2]T,Ψ0=Ψ
k≠0时:
(24)
式中
Qk=[q2(2k-1)+1,q2(2k-1)+2,q2(2k-1)+3,q2(2k-1)+4]T
(6)针对独立电力系统电力电子设备动态、功能级动态、结构级动态三种层次的动态特性,合理选择傅里叶分解的阶数N,对独立电力系统的广义状态空间平均模型进行化简。若取N=1,则最终的一阶广义状态空间平均模型如式(25)所示;若取N=2,则最终的二阶广义状态空间平均模型如式(26)所示。
(25)
(26)
4.2 仿真验证
以建立的简化广义状态空间平均模型为基础,进行时域仿真与广义状态空间平均模型仿真对比验证,电路参数如表1所示。
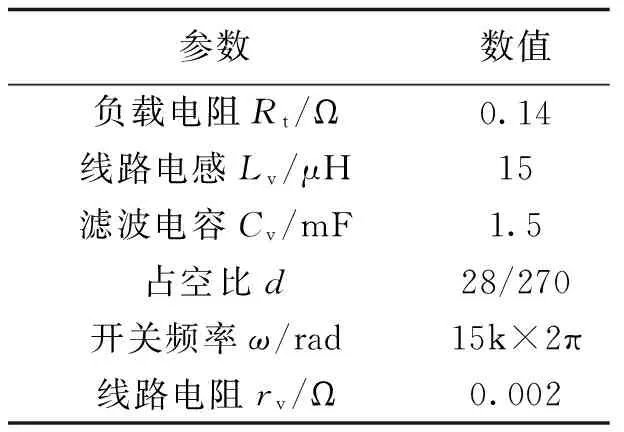
表1 Buck变换器电路参数Tab.1 Parameters of Buck converter
仿真时间设置为2ms,时域仿真与广义状态空间平均一阶、二阶模型进行仿真对照。图3为Buck变换器输出电压VCv的变化曲线。可以看出,暂态运行阶段,一阶、二阶广义状态空间平均模型与时域仿真模型具有相同的变化趋势,但由于广义状态空间平均模型忽略了一定时间尺度的动态特性,所以与时域仿真模型之间存在差异,但这种差异随着阶数的增加逐渐减小。
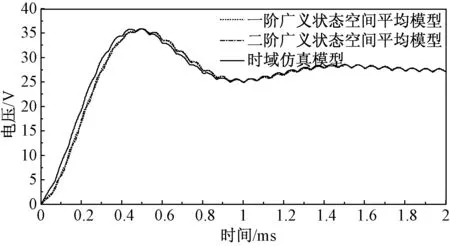
图3 输出电压仿真波形Fig.3 Simulative waveforms of output voltage
当系统达到稳态后,一阶、二阶广义状态空间平均模型与时域仿真模型的输出曲线基本重合,表明在稳态情况下广义状态空间平均模型阶数对仿真的精度影响不明显。图4为1.87~2ms输出电压曲线的局部放大图,可以看出随着阶数的增加(一阶到二阶),广义状态空间平均模型与时域仿真模型之间的差异性越来越小,仿真精度相应提高。

图4 输出电压仿真波形(局部放大)Fig.4 Simulative waveforms of output voltage (Enlarged)
图5为Buck变换器输入电流Iv的仿真变化曲线,三种模型的电流仿真曲线同样具有相同的变化趋势,但由于广义状态空间平均模型忽略了一定时间尺度的动态特性,所以与时域仿真模型之间存在差异,但这种差异随着阶数的增加逐渐减小。
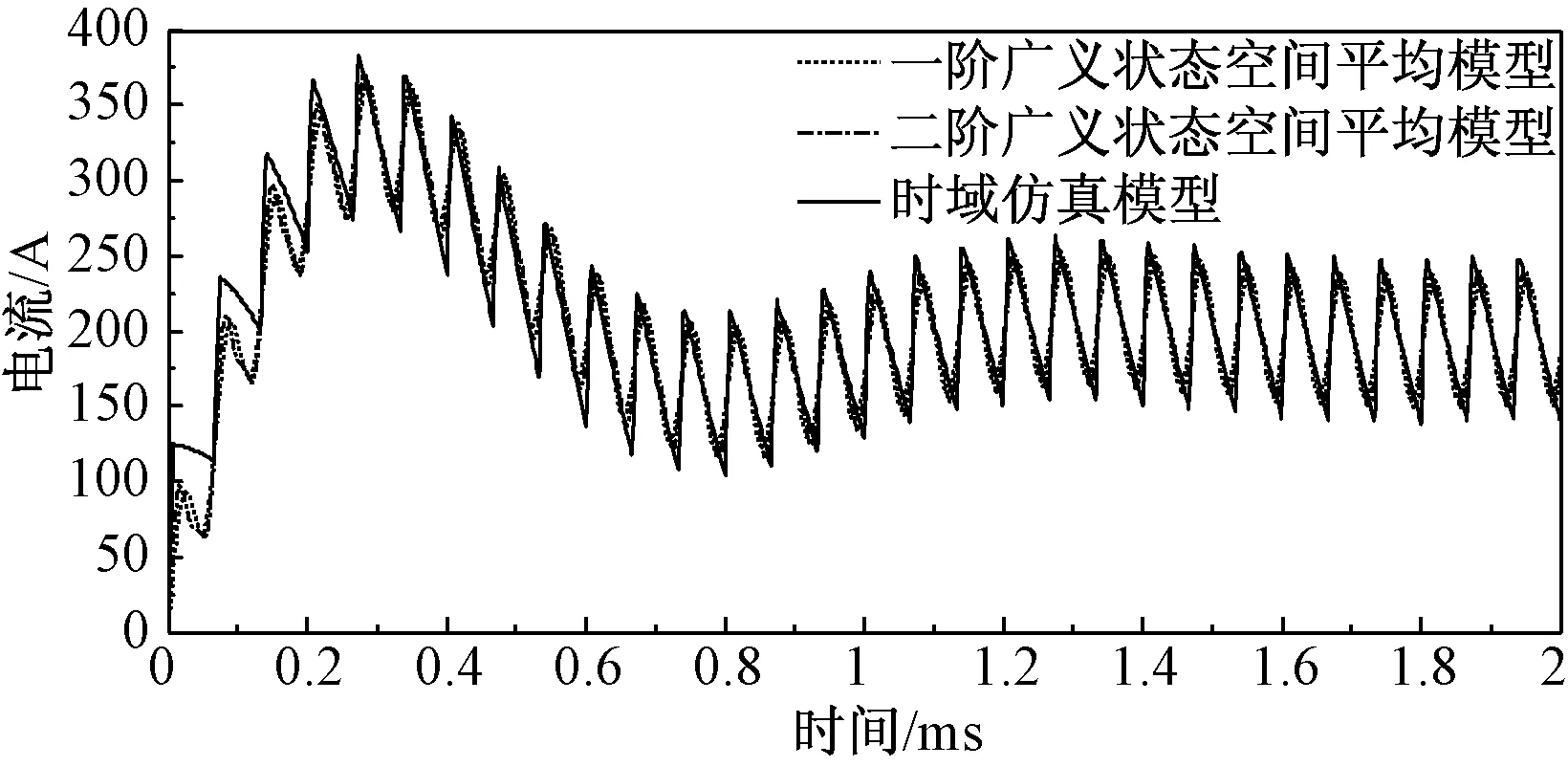
图5 输入电流仿真波形Fig.5 Simulative waveforms of input current
当系统达到稳态后,一阶、二阶广义状态空间平均模型与时域仿真模型的输出曲线基本重合,表明在稳态情况下广义状态空间平均模型阶数对仿真的精度影响不明显。图6为1.87~2ms之间输出电流曲线的局部放大,随着广义状态空间平均模型阶数的增加,仿真结果与时域仿真模型之间的差异性越来越小,仿真精度相应提高。

图6 输入电流仿真波形(局部放大)Fig.6 Simulative waveforms of input current (Enlarged)
值得指出的是,本文以Buck变换器为例,目的是说明广义状态空间平均模型的建模过程,针对独立电力系统的其他部件,如发电机、变压器、整流器、逆变器等,本文所提出的建模过程依然具有通用性。
5 结论
本文提出一种基于广义状态空间平均模型的建模方法,并应用于独立电力系统的建模领域,得出如下结论:
(1) 广义状态空间平均模型阶数与独立电力系统动态特性具有相似的变化趋势,适用于含多时间尺度动态特性的独立电力系统建模。
(2) 广义状态空间平均建模方法与时域仿真法相比,稳态时具有相似的精度;暂态时,随着广义状态空间平均模型阶数的增加,其仿真结果越接近于时域仿真模型。
[1] 陈来军,梅生伟,许寅,等(Chen Laijun, Mei Shengwei, Xu Yin, et al.). 未来电网中的独立电力系统模式(A new pattern of future power grids: Isolated power system)[J].电力科学与技术学报(Journal of Electric Power Science and Technology),2011,26(4):30-36.
[2] 张雪敏, 陈来军, 梅生伟(Zhang Xuemin,Chen Laijun,Mei Shengwei). 输入状态稳定理论及其独立电力系统应用(Input-to-output stability theory and its application on isolated power system) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2012,31(4):58-61.
[3] 陈鹏伟,陶顺,杨洋,等(Chen Pengwei, Tao Shun, Yang Yang, et al.).电磁-机电暂态混合仿真接口交互信息限制性分析(Analysis of transinformation limit for electromagnetic-electromechanical hybrid simulation) [J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy),2016,35(5):1-7.
[4] M A Lemaire, L Montealegre Lobo, J Mahseredjian, et al. Simulation of aircraft electrical power systems: Tools and challenges[A]. Canadian Aeronautics and Space Institute AERO 2011 Conference[C]. Montreal, Canada, 2011. 251-259.
[5] 马凡,马伟明,付立军(Ma Fan, Ma Weiming, Fu Lijun). 一种非线性多时间尺度系统模型降阶方法(A model order reduction method for nonlinear multi-time scale systems)[J]. 中国电机工程学报(Proceedings of the CSEE),2013,33(16):162-170.
[6] 李鹏,于浩,王成山,等(Li Peng, Yu Hao, Wang Chengshan, et al.). 基于Krylov子空间的大规模配电网络模型整体化简方法(Model order reduction of large scale distribution grid based on Krylov subspace method)[J]. 电网技术(Power System Technology),2013,37 (8):2343-2348.
[7] 李鹏,丁承第,王成山,等(Li Peng, Ding Chengdi, Wang Chengshan, et al.).基于多核心处理器的分布式发电微网系统暂态并行仿真方法(A parallel algorithm of transient simulation for distributed generation system based on multi-core CPU)[J]. 中国电机工程学报(Proceedings of the CSEE),2013,33(16):171-178.
[8] 王成山,黄碧斌,李鹏, 等(Wang Chengshan, Huang Bibin, Li Peng, et al.). 自动微分技术在分布式发电系统暂态仿真中的应用(Application of automation differentiation technique to transient simulation of distributed generation system) [J]. 电力系统自动化(Automation of Electric Power Systems),2010,34(23):71-75.
[9] Leonardo Montealegre Lobo, Christian Dufour. Real-time simulation of more-electric aircraft power systems[A]. 15th European Conference on Power Electronics and Applications[C]. Lille, France, 2013. 1-10.
[10] E Lavopa, P Zanchetta, M Sumner, et al. Real-time estimation of fundamental frequency and harmonics for active shunt power filters in aircraft electrical systems [J]. IEEE Transactions on Industrial Electronics, 2009, 56(8) :2875-2884.
[11] R D Middlebrook, S Cuk. A general unified approach to modeling switching converter power stages[A]. IEEE Power Electronics Specialists Conference, PESC’76[C]. 1976.18-34.
[12] T Wu, S V Bozhko, G M Asher, et al. Fast reduced functional models of electromechanical actuators for more-electric aircraft power system study[A]. 2008 SAE Power System Conference[C]. 2008. 562-570.
[13] T Wu, S V Bozhko, G M Asher, et al. A fast dynamic phasor model of autotransformer rectifier unit for more electric aircraft[A]. 35th Annual Conference of IEEE Industrial Electronics, IECON’09 [C]. Porto, Portugal, 2009.2531-2536.
[14] K-N Areerak, S V Bozhko, G M Asher, et al. Stability analysis and modeling of AC-DC system with mixed load using DQ-transformation method[A]. IEEE International Symposium on Industrial Electronics[C]. Cambridge, UK, 2008.19-24.
[15] L Han, J Wang, D Howe. State-space average modelling of 6- and 12-pulse diode rectifiers[A]. The 12th European Conference on Power Electronics and Applications[C]. Aalborg, Denmark, 2007. 1-10.
[16] A F Witulski,R W Erickson. Extension of state-space averaging to resonant switches and beyond[J]. IEEE Transactions on Power Electronics, 1990, 5 (1): 98-109.
[17] P J Norman, S J Galloway, G M Burt, et al. Evaluation of the dynamic interactions between aircraft gas turbine engine and electrical system[A]. 4th IET Conference on Power Electronics, Machines & Drives[C]. 2008. 671-675.
[18] S R Sanders, J M Noworolski, X Z Liu, et al. Generalized averaging method for power conversion circuits[J]. IEEE Transactions on Power Electronics, 1991, 6(2): 251-259.
Modeling method of isolated power system based on generalized state space averaging
YANG Zhan-gang1, WU Hui-dong1, QU Jun-chao1, CHE Yan-bo2
(1. College of Electronic Information and Automation, Civil Aviation University of China,Tianjin 300300, China; 2. Key Laboratory of Smart Grid of Ministry of Education,Tianjin University, Tianjin 300072, China)
The isolated power system is a fast developing trend with the widely used power electronics. In order to investigate the overall system performance under normal and abnormal scenarios, the generalized state space averaging modeling method was proposed. Through replacing the state variables of the isolated power system time-variant nonlinear differential equations with their complex Fourier coefficients over a desired time interval, the generalized state space averaged model of isolated power systems was built. Depending on the different operating conditions, the dynamic characteristics of the isolated power system on different time scales were analyzed, and the simplified generalized state space averaging model was achieved by increasing or decreasing the order of Fourier coefficients. This modeling method can identify the isolated power system operating conditions and the dynamic characteristics. It can be used as time-domain model in systems analysis and design, and also it can be used as state-space model in steady state analysis. It is demonstrated that the generalized state space averaging model of the isolated power system can be used to the steady and transient analysis of different isolated power system with high simulation speed and good accuracy.
isolated power system; generalized state space averaging; dynamic characteristics; Fourier coefficients
2016-06-13
国家自然科学基金项目(51407185; U1533126)、 中国民航大学实验技术创新基金项目(17-14-03)、 中国民航大学科研启动基金项目(2011-QD02X)
杨占刚(1979-), 男, 河北籍, 讲师, 博士, 研究方向为微电网与独立电力系统; 吴惠东(1991-), 男, 江西籍, 硕士研究生, 研究方向为独立电力系统建模与仿真。
V242.3
A
1003-3076(2016)12-0012-08
