计及UPFC的电力系统网损优化控制研究
2016-05-03王秀云杨金成
王秀云, 李 超, 杨金成, 李 丹
(1. 东北电力大学电气工程学院, 吉林省 吉林市 132012; 2. 新疆电力科学研究院, 新疆 乌鲁木齐 830011; 3. 延边供电公司调控中心, 吉林 延吉 133000)
计及UPFC的电力系统网损优化控制研究
王秀云1, 李 超1, 杨金成2, 李 丹3
(1. 东北电力大学电气工程学院, 吉林省 吉林市 132012; 2. 新疆电力科学研究院, 新疆 乌鲁木齐 830011; 3. 延边供电公司调控中心, 吉林 延吉 133000)
将统一潮流控制器(UPFC)等效为节点附加注入功率,控制变量增加了UPFC等值模型中串联电压源电压的幅值和相位,以及并联电流源电流的无功分量等控制参数,建立计及UPFC的无功优化模型。由UPFC控制参数与安装线路的电流和端点电压,推导出UPFC运行容量计算公式,结合UPFC价格与容量函数关系,确立UPFC参数与价格的数学关系,将其应用于无功优化研究,以收益最大为目标函数,分析UPFC的降损经济效益。以IEEE30节点系统为例进行仿真分析,结果表明,UPFC不仅具有良好的降损特性,而且获得的收益能够弥补自身价格昂贵的不足,具有实际应用价值。
UPFC; 网损优化; 经济收益
1 引言
电力系统无功优化根据已知的电网结构参数,在不超出安全运行约束范围的情况下,通过控制可调参数使网络的无功功率合理分布,进而减少有功损耗,保证系统运行具有良好的安全性和经济性[1,2]。随着现代电力电子控制技术的发展,柔性交流输电技术(FACTS)在电网运行中得到了应用[3,4]。统一潮流控制器(UPFC)作为FACTS家族的代表,综合了多种FACTS设备的功能,具有串并联补偿、移相和端电压调节的作用,可快速灵活地调整线路输送功率,实现功率的合理分配,降低功率损耗和发电成本,提高系统的经济性[5,6]。由于UPFC装置价格昂贵,其降损收益能否弥补安装投资费用,是衡量UPFC网损优化经济性好坏的重要评价指标,因此,本文采用UPFC等值功率注入模型,以经济效益最大为优化目标,建立UPFC网损优化数学模型,考虑UPFC自身运行费用和网损节约成本,分析利用UPFC进行网损优化控制的经济效益。
2 UPFC等值功率注入模型
统一潮流控制器输出体现在对系统进行电压控制和调节线路潮流等功能上,当其工作在稳定运行状态时,忽略控制器内部的相互影响,将UPFC等值为一个串联电压源VT和并联电流源Ish的组合[7]。并联电流源又可分解为有功分量It和无功分量Iq,其中,It与Vi同相,而Iq与Vi正交,即
(1)
式中,arg()表示向量的角度。UPFC等效电路模型和注入功率模型分别如图1和图2所示。
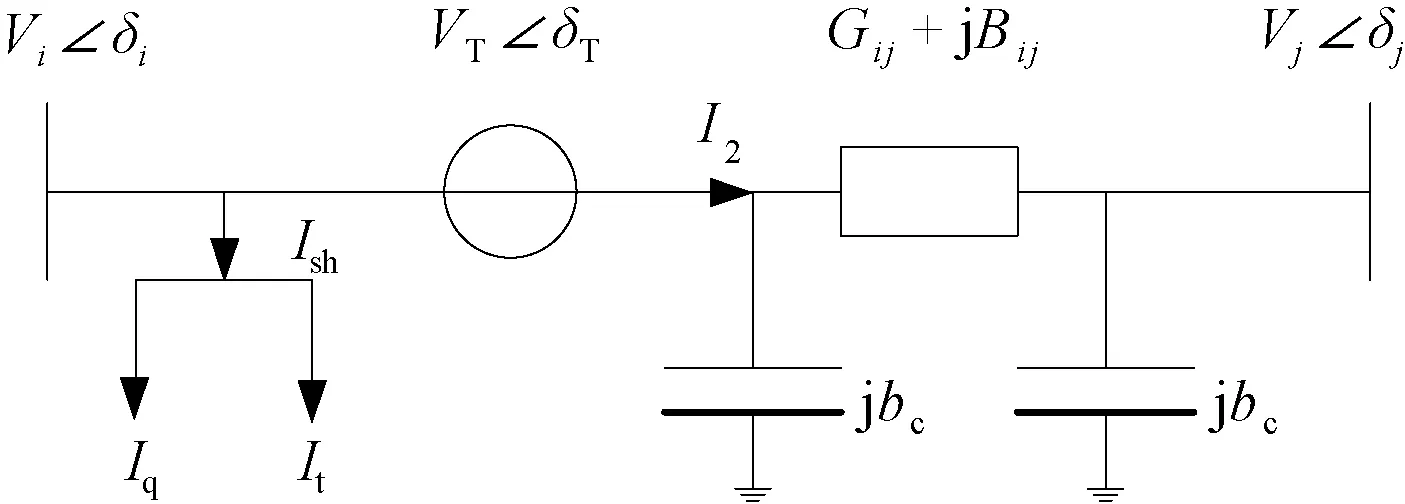
图1 UPFC等效电路模型Fig.1 Equivalent circuit model of UPFC
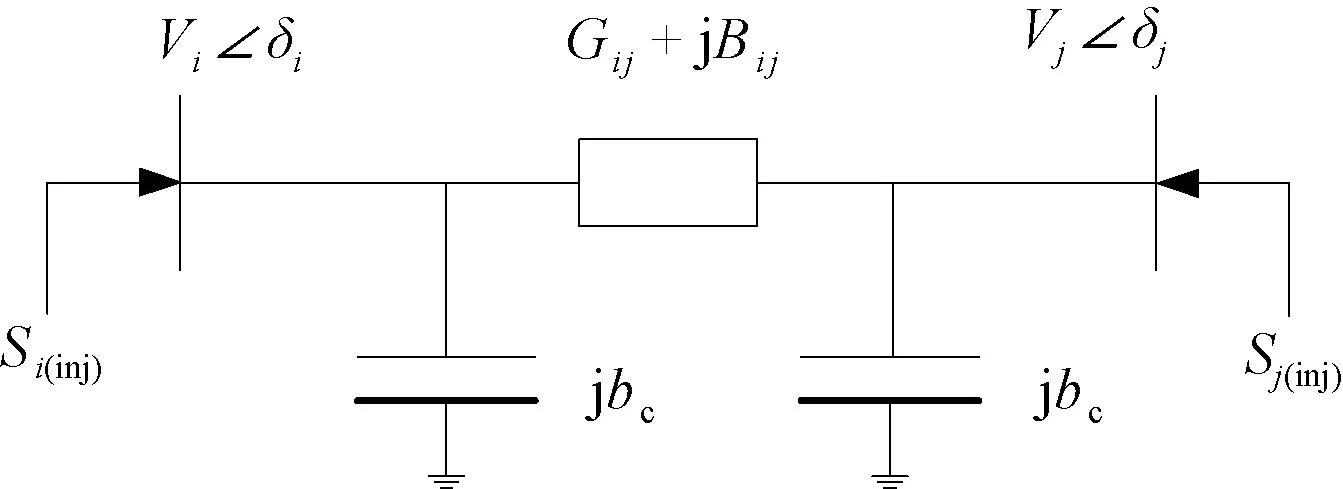
图2 UPFC等效注入功率模型Fig.2 Power injection model of UPFC
由图1可列出含UPFC线路两侧节点i和j的附加注入电流ΔIi和ΔIj的表达式:
(2)
则节点i侧等效注入功率为:
(3)
由于UPFC的串联电压源和并联电流源的模值和相位可以连续调节,并且UPFC的并联电流源Ish和串联电压源VT之间存在有功功率平衡约束[8],即运行时满足:
(4)
节点i侧等效注入功率为:
(5)
同理,j侧等效注入功率为:
(6)
对比式(3)和式(5)可知,UPFC的4个独立运行控制参数变为了3个,即串联电压源电压的幅值VT和相位δT,以及Ish的无功分量Iq。本文采用UPFC等值功率模型,在潮流计算过程中没有修改节点导纳矩阵的阶数,可以有效减少无功优化问题的约束条件,有利于降低问题求解的复杂度。
3 UPFC网损优化经济收益
系统安装UPFC后,通过无功优化降低了系统的网络有功功率损耗,节约了输电成本,即为网损优化收益。在进行计及UPFC装置的网损优化控制经济性分析过程中,网损优化收益是重要评价指标,但UPFC装置自身非常昂贵,不能仅凭网损优化收益来分析其经济性,有必要将UPFC的运行成本与降低网损带来的经济效益进行比较,建立经济性评价指标,分析其经济效益。
UPFC的运行成本由其容量和价格决定,而价格和容量之间满足函数映射关系,而在UPFC等值功率注入模型中,其容量由运行参数决定,因此,UPFC运行成本与运行参数相关联。在优化过程中,不同的UPFC运行参数获得的网损优化收益不同,这是智能算法求解UPFC网损优化经济性问题的基础,也是建立UPFC网损优化经济性评价指标的关键。图3为UPFC网损优化控制经济收益图。

图3 经济收益计算示意图Fig.3 Diagram of calculating economic benefits
3.1 UPFC容量
UPFC的容量是指其串联侧换流器与并联侧换流器的容量之和,而各换流器的容量取决于其与系统间的有功和无功功率的交换量[9]。串联侧换流器容量根据UPFC串联电压幅值与安装线路电流确定,并联侧换流器容量分为有功功率和无功功率两部分求得,无功功率由安装点电压和电流无功分量求得,而由UPFC的功率平衡方程可知,并联侧有功功率与串联侧有功功率相等,因此,UPFC容量S的计算公式为:
(7)
3.2 UPFC价格函数
UPFC价格与容量相关联,若S(MV·A)表示容量,根据文献[10],单位容量UPFC的价格C1($/(kV·A))计算如下:
C1=0.0003S2-0.2691S+188.22
(8)
因此,统一S与C1的单位后,可得UPFC的价格C2($/)计算公式如下:
C2=1000C1S=0.3S3-269.1S2+188220S
(9)
3.3 网损节约成本
电力系统无功优化数学模型中,网损ΔP的计算公式为:
(10)
若ΔP0代表优化前的初始有功网损,ΔPUPFC表示安装UPFC后的有功网损,将标幺值换算成有名值,则网损年节约成本C3($)的计算公式为:
C3=(ΔP0-ΔPUPFC)SB·8760·d·0.1611
(11)
式中,SB为功率基准值(MV·A);d为实时电价(元/(kV·A)),人民币兑美元汇率取0.1611。
3.4 经济收益
将网损优化收益与UPFC投资成本进行比较,便得到以经济效益Sy($)的数学表达式,如式(12)所示:
Sy=C3·yn-C2
(12)
式中,yn为UPFC经济使用寿命周期。
4 UPFC网损优化的经济性
4.1 目标函数
目标函数的选取对于优化问题求解至关重要,决定了研究的大致方向和解的精确性。考虑经济因素时,UPFC网损优化的经济收益与降损收益均与UPFC的参数有关,从而与通过参数确定的容量有关,而与以UPFC的容量为自变量,不同目标函数为因变量的函数关系表达式有所不同,因此,不同的经济目标函数极值和极值点均不同。本文从经济角度出发,以经济收益最大为优化目标,研究其降损经济效益。目标函数如式(13)所示:
f=maxSy
(13)
4.2 约束条件
约束条件分为等式约束和不等式约束,等式约束即为节点功率平衡约束,不等式约束包括控制变量和状态变量约束[11]。节点功率平衡方程中节点分为以下两类。
(1)安装UPFC支路两端节点
(14)
(2)其他节点
(15)
控制变量约束为:
(16)
状态变量约束为:
(17)
式中,VGimax、VGimin分别为发电机i的电压幅值上、下限;Timax、Timin分别为变压器i的变比的上、下限;Qcimax、Qcimin分别为补偿装置i的补偿容量的上、下限;VTmax、VTmin和Iqmax、Iqmin分别为UPFC串联电压源的幅值VT和并联电流源无功分量Iq的上、下限;VLimax、VLimin分别为负荷i的电压幅值的上、下限;QGimax、QGimin分别为发电机i的无功出力上、下限[12]。
4.3 求解算法
本文应用遗传算法求解UPFC的网损优化经济性问题,染色体编码信息分别包括连续变量和离散变量,前者含发电机端电压VG和UPFC的控制参数(VT、δT、Iq),后者对应有载调压变压器分接头T和并联补偿电容器的档位C,因此,解码后的个体可表示为:
[VG1,…,VGNg,VT1,δT1,Iq1,…,VTNu,δTNu,
ITNu,C1,…,CNc,T1,…,TNt]
式中,Ng、Nu、Nc和Nt分别为发电机节点数、UPFC装置台数、并联电容补偿点总数和变压器台数。
5 算例分析
应用MATLAB7.8.0编制遗传算法程序,功率基准值SB设为100MV·A。以IEEE30节点系统为例进行仿真验证。系统共由30个节点和41条支路组成,其中,发电机节点6个,分别是1、2、5、8、11、13,发电机端电压为连续变化,节点1为平衡节点;有载调压变压器支路4条,分别是(6,9)、(6,10)、(4,12)、(28,27),变压器变比的步长为0.025pu;无功补偿节点2个,分别是节点10和24,补偿电容器的调节步长分别为0.1pu和0.02pu。系统状态变量变化范围见表1,系统参数参见文献[13]。支路4-6靠近节点4处安装UPFC,其控制参数VT、Iq和δT均可在一定范围内连续调节,其模值受容量等因素的约束,而相角δT在0~2π之间任意变化,UPFC的控制参数取值范围见表2。
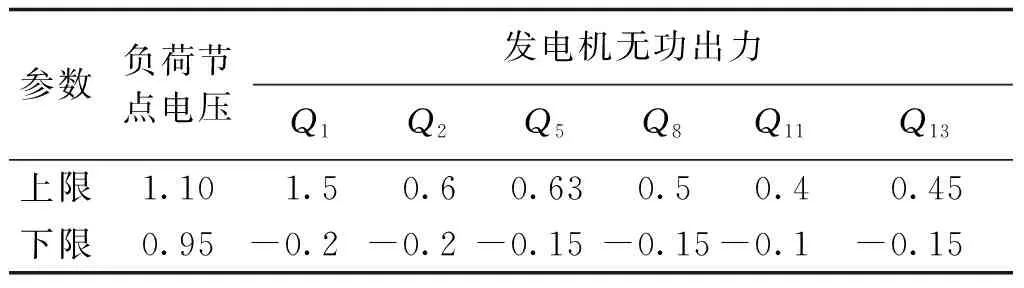
表1 发电机无功出力及负荷节点电压上下限Tab.1 Generator’s reactive power and voltage limits (单位:pu)

表2 UPFC控制参数VT、Iq的取值范围Tab.2 Limits of UPFC control parameters (单位:pu)
以经济效益最大为优化目标,进行计及UPFC的网损优化控制经济性分析算例仿真时,实时电价d取0.5元/(kW·h),UPFC经济使用寿命周期yn取30年[14]。采用遗传算法进行求解,种群规模选为50,最大迭代次数为50次。
表3和表4为优化后的控制变量和UPFC参数取值。分别与表1和表2的限值进行比较,所有的控制变量均在要求范围内,且有一定的裕度。

表3 优化后的控制变量Tab.3 Optimization status of control variables (单位:pu)
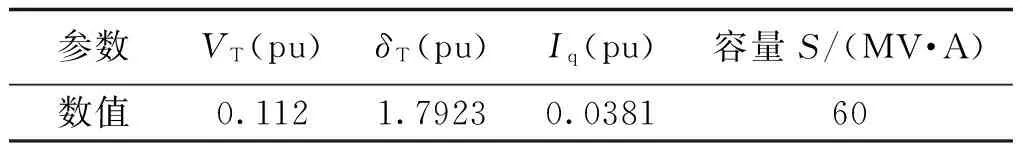
表4 优化后的UPFC参数Tab.4 UPFC parameters of optimal solutions
表5为计及UPFC优化的结果。安装UPFC后系统的网损较之前降低了22.3%,从收益Sy优化结果来看,减小网损节约的发电成本C3弥补了安装UPFC增加的投资费用C2,投资回收率超过50%。
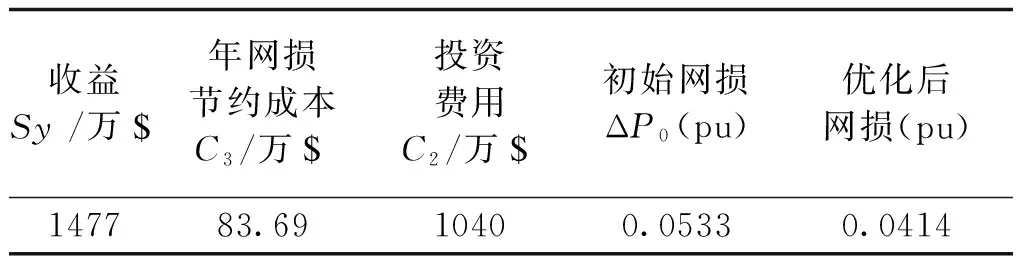
表5 计及UPFC无功优化经济性指标Tab.5 Economic indicators of optimization program with UPFC
图4为经济收益及其对应的有功网损的优化曲线,二者结合来看,网损最小时是第5代,而经济收益却不是最大,较最大经济收益减少61%,两者变化趋势不是一一对应关系,说明计及UPFC的经济性研究时不应只考虑减小网损获得的收益,还要考虑UPFC的投资费用。图5为系统优化后的节点电压曲线,各节点电压均在要求的限值内,说明优化后的系统电压质量得到了保证。
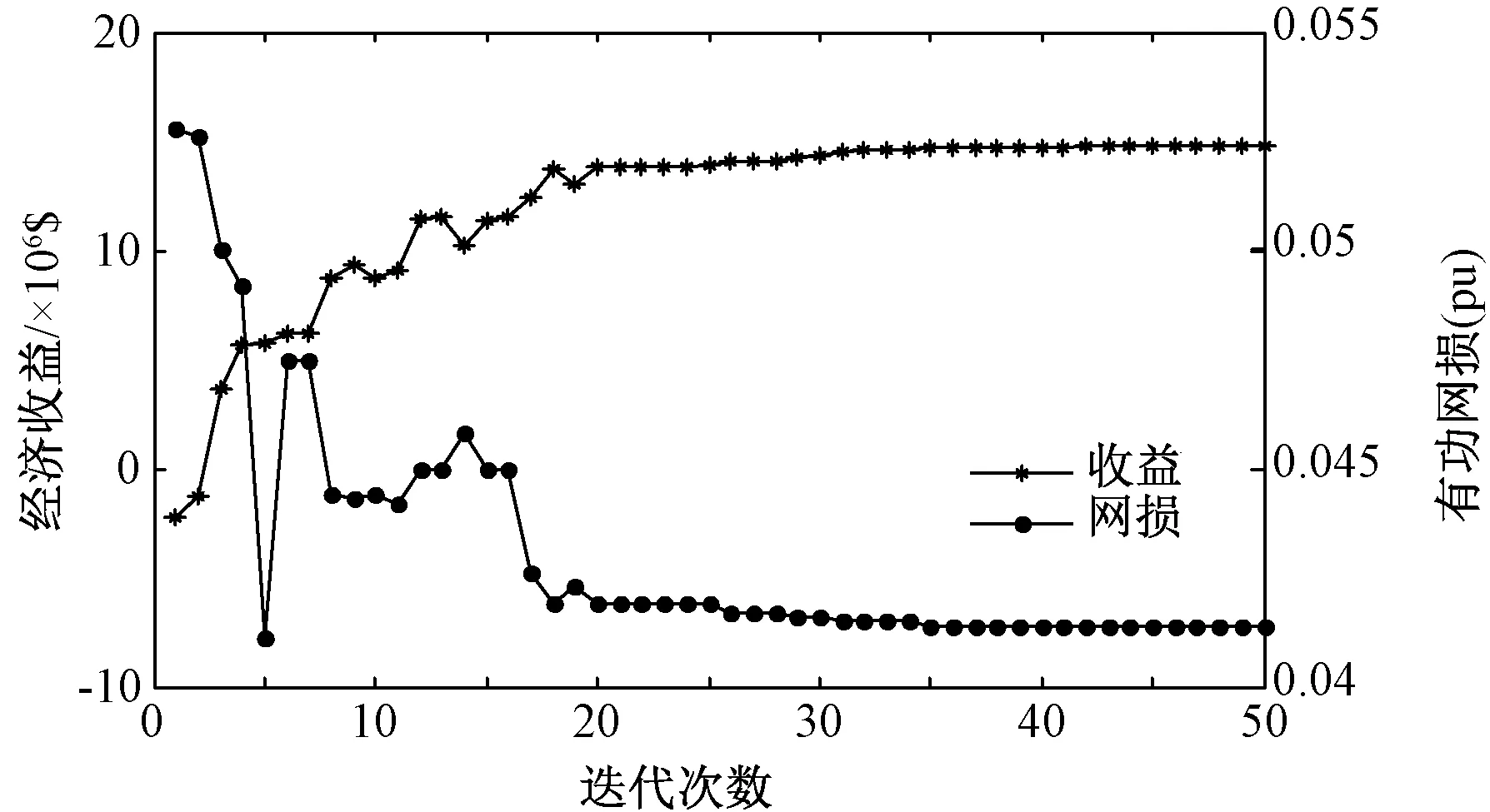
图4 收益和网损优化曲线Fig.4 Optimization curves of benefits and active power loss

图5 电压分布曲线Fig.5 Curve of bus voltage
6 结论
首先,建立计及UPFC的无功优化的数学模型过程中,UPFC采用了等效注入功率模型,避免了增加潮流计算中节点导纳矩阵的阶数,有效地降低了问题的求解难度。将UPFC的运行参数加入到控制变量中,体现了UPFC对线路潮流的控制作用。
其次,本文考虑了系统安装UPFC的投资费用和减小网损获得的经济收益,建立了UPFC降损经济收益数学模型,说明UPFC的运行参数是无功优化和UPFC投资费用的联系纽带,也是进行UPFC降损经济性分析的基础。
最后,以IEEE30节点系统为算例进行仿真,仿真结果表明,UPFC接入电力系统,以经济收益最大为目标函数的优化方案不仅降低了系统的网络损耗,改善了电压质量,而且能够获得可观的经济收益,弥补了其价格昂贵的不足,为UPFC的实际应用提供了理论依据。
[1] 李晶,王素华,谷彩连(Li Jing, Wang Suhua, Gu Cailian).基于遗传算法的含分布式发电的配电网无功优化控制研究(Research of reactive power optimization control in distribution networks based on genetic algorithm)[J].电力系统保护与控制(Power System Protection and control),2010,38(6):60-63.
[2] 赵亮,吕剑虹(Zhao Liang, Lv Jianhong).基于改进遗传算法的风电场多目标无功优化(Multi-objective reactive power optimization of wind farm based on improved genetic algorithm)[J].电力自动化设备(Electric Power Automation Equipment),2010,30(10):84-88.
[3] 黄柳强,郭剑波,卜广全,等(Huang Liuqiang, Guo Jianbo, Pu Guangquan,et al.).FACTS协调控制研究进展及展望(Research process and prospect of FASTS coordinated control)[J].电力系统保护与控制(Power System Protection and control),2012,40(5):138-147.
[4] 孙元章,刘前进(Sun Yuanzhang, Liu Qianjin).FACTS控制技术综述——模型,目标与策略(Summary of FACTS control technology - Model, target and strategy)[J].电力系统自动化(Automation of Electric Power Systems),1999,23(6):1-7.
[5] 刘黎明,康勇,陈坚,等(Liu Liming, Kang Yong, Chen Jian, et al.). UPFC的交叉耦合控制及潮流调节能力分析(Cross-coupling control scheme and performance analysis for power flow control of UPFC)[J].中国电机工程学报(Proceedings of the CSEE),2007,27(10):42-48.
[6] 颜伟,朱继忠,孙洪波,等(Yan Wei, Zhu Jizhong, Sun Hongbo, et al.).UPFC的潮流控制与暂态稳定性研究(Study of power flow control and transient stability UPFC)[J].中国电机工程学报(Proceedings of the CSEE),2000,20(12):58-62.
[7] 桂帆,江道灼,吕文韬,等(Gui Fan, Jiang Daozhuo, Lv Wentao, et al.).限流式统一潮流控制器参数设计及优化(Parameter design and optimization of flow limiting unified power flow controller)[J].电力自动化设备(Electric Power Automation Equipment),2013,33(11):160-164.
[8] 李虎成,於益军,李峰,等(Li Hucheng, Yu Yijun, Li Feng, et al.).含UPFC网络的潮流计算及稳态特性仿真分析(Power flow calculation and steady state simulation analysis of power systems with UPFCs)[J].电网与清洁能源(Power System and Clean Energy),2013,29(4):1-6.
[9] 唐爱红,朱鹏程,程时杰,等(Tang Aihong, Zhu Pengcheng, Cheng Shijie, et al.). 统一潮流调节器实验装置的研究(Study of the test equipment for UPFC)[J].电工技术学报(Transactions of China Electrotechnical Society),2006,21(6):122-126.
[10] L J Cai, I Erlich, G Stamtsis. Optimal choice and allocation of FACTS devices in deregulated electricity market using genetic algorithms[A]. IEEE PES Power Systems Conference and Exposition[C]. 2004. 1:201-207.
[11] 王秀云,李超,赵宇,等(Wang Xiuyun, Li Chao, Zhao Yu, et al.).仿生粒子群算法在电力系统无功优化中的应用(Application of parallel adaptive particle swarm optimization algorithm in reactive power optimization of power system)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(7): 75-79
[12] 张燕,许伟伟(Zhang Yan, Xu Weiwei).基于粒子群-差异进化混合算法的电力系统无功优化(Reactive power optimization based on improved particle swarm optimization algorithm)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(9):48-51.
[13] Q H Wu, Y J Cao, J Y Wen. Optimal reactive power dispatch using an adaptive genetic algorithm[J]. International Journal of Electrical Power & Energy Systems, 1998, 20(8): 563-569.
[14] 赵渊,杨晓嵩,谢开贵(Zhao Yuan, Yang Xiaosong, Xie Kaigui).UPFC对电网可靠性的灵敏度分析及优化配置(Sensitivity analysis and optimal allocation of UPFC to power system reliability)[J].电力系统自动化(Automation of Electric Power Systems), 2012, 36(1): 55-60.
Research of loss optimization in power system considering UPFC installation
WANG Xiu-yun1, LI Chao1, YANG Jin-cheng2, LI Dan3
(1. School of Electrical Engineering,Northeast Dianli University,Jilin 132012, China;2. State Grid Electric Power Research Institute of Xinjiang,Urumqi 830011, China;3.Yanbian Power Supply Company,Yanji 133000, China)
This paper has established a reactive power optimization model with Unified Power Flow Controller (UPFC). The parameters of UPFC, such as amplitude and phase of the voltage source in series and reactive component of parallel current source in the equivalent model, are added into control variables. While UPFC is equivalent to an additional power injection for the nodes, the operational capacity of UPFC is calculated by combining UPFC parameters and endpoints voltage and current of installation lines. Then the mathematical relationship of parameters and price of UPFC is put forward, which is applied to the reactive power optimization. The price of UPFC is compared with the saving of energy cost by reducing power loss and the economic benefit for UPFC is studied to gain the maximal earnings. Finally simulation results in IEEE30 bus system show that not only UPFC has good features of reducing reactive power loss, but its earning can also make up for the defect of its expensive price. UPFC has practical value.
UPFC; reactive power loss optimization; economic benefit
2015-12-29
王秀云(1977-), 女, 吉林籍, 副教授/硕导, 硕士, 研究方向为电力系统优化运行; 李 超(1988-), 男, 吉林籍, 硕士研究生, 研究方向为电力系统无功优化。
TM712
A
1003-3076(2016)12-0065-06
