基于有限公式法的水冷永磁同步电机三维温度场分析
2016-05-03佟文明舒圣浪朱高嘉程雪斌
佟文明, 舒圣浪, 朱高嘉, 程雪斌
(国家稀土永磁电机工程技术研究中心, 沈阳工业大学, 辽宁 沈阳 110870)
基于有限公式法的水冷永磁同步电机三维温度场分析
佟文明, 舒圣浪, 朱高嘉, 程雪斌
(国家稀土永磁电机工程技术研究中心, 沈阳工业大学, 辽宁 沈阳 110870)
有限公式法是一种直接从物理规律出发、借助定义在两嵌套网格几何元素上的全局变量构造离散方程的新型数值计算方法。在建立有限公式法温度场数学模型的基础上,本文讨论了基于映射网格的对流散热边界处理及其编程实现,并给出了有限公式法温度场模块化编程的基本思路。最后,以对一台20kW水冷永磁同步电机三维温度场的分析,研究了冷却水流速、冷却水温与电机温升分布的规律;并以电机温升试验值、同一网格下的有限元法计算值验证了所编制程序计算的准确性、可靠性。
有限公式法; 温度场; 边界条件; 永磁同步电机; 数值计算
1 引言
有限公式法直接从物理规律出发,以定义在时空元素(空间上的点、线、面、体与时间上的时间点、时间段)上的全局变量为离散变量,结合网格拓扑结构和本构关系得到离散方程。有限公式法采用两嵌套网格结构,在原网格为非结构网格时,映射网格为任意的多面体,对具有复杂边界的物理场问题适用性好,计算精度与有限元法相当[1,2]。文献[3]应用有限公式法对简单几何体的三维稳态电场与瞬态温度场耦合问题进行了研究,其计算值与有限元计算结果吻合;文献[4,5]应用有限公式法对电机内部二维涡流场及其电磁性能进行了计算,验证了有限公式法在复杂求解域问题上的适用性,并介绍了有限公式法的边界条件处理。根据已有文献[1-5],有限公式法在复杂几何体三维温度场计算上的应用还较少。
本文基于有限公式法理论,建立了有限公式法温度场数学模型,给出了有限公式法下温度场对流散热边界处理与编程实现的方法。在编写模块化计算程序的基础上,应用其对一台20kW水冷永磁同步电机三维温度场进行了计算,分析了冷却水流速、冷却水温与电机温升分布的规律,并以电机温升试验值、同一网格下的有限元法计算值验证了所编制程序的正确性。
2 温度场数学模型与边界条件
2.1 温度场数学模型
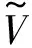
(1)
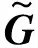
有限公式法下的温度场离散从原网格节点温度出发,通过拓扑方程与本构方程得到映射网格体上的热通量守恒方程。有限公式法温度场离散过程如图1所示。
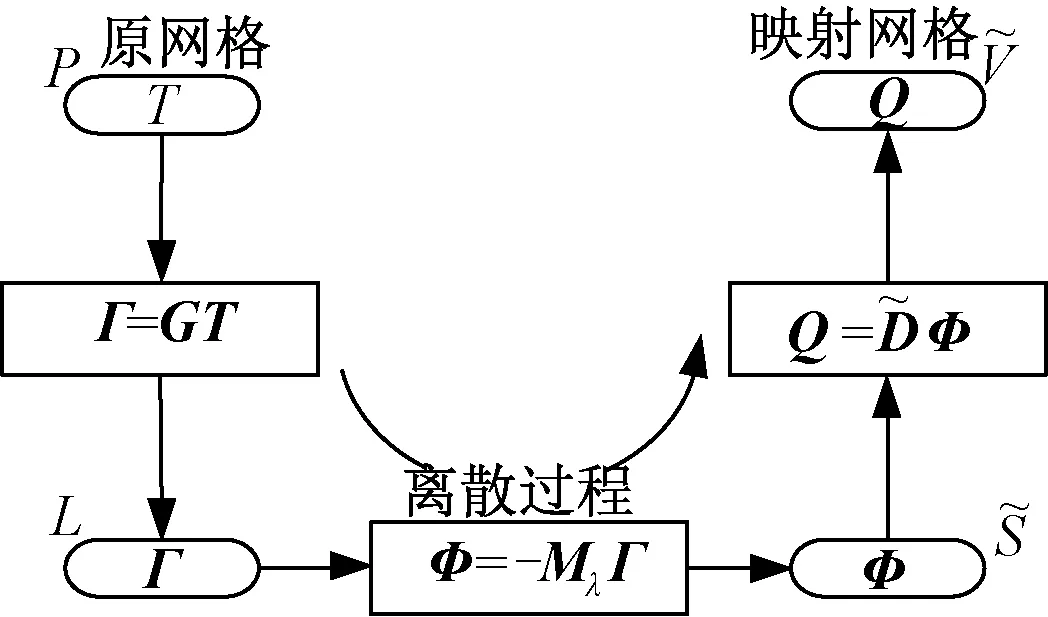
图1 有限公式法温度场离散过程Fig.1 Temperature field discrete process of FFM
图1给出的有限公式法温度场离散过程可简单地描述为:由定义在原网格节点上的温度T得到定义在原网格线上的温度差Γ,进而根据温度场本构关系得到原网格线对应映射网格面上的热通量Φ;最后,根据原网格节点与映射网格体的一一对应关系得到映射网格体上的总热通量Q。根据式(1)中的离散算子间的关系式,有限公式法温度场数学模型为:
(2)
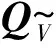
2.2 边界条件
有限公式法的对流散热边界为:
(3)
式中,Mα为散热系数矩阵;T0为对流散热边界参考温度。
有限公式法通过对映射网格体列写热通量守恒方程来构造代数离散方程,自然的,其对流散热边界为映射网格面。原网格与映射网格的对应关系如图2所示,其中实线为原网格,虚线为映射网格。通过映射网格体(二维情形下包围原网格点的面即为映射网格体)上的热通量可由原网格微元上的热通量累加得到。
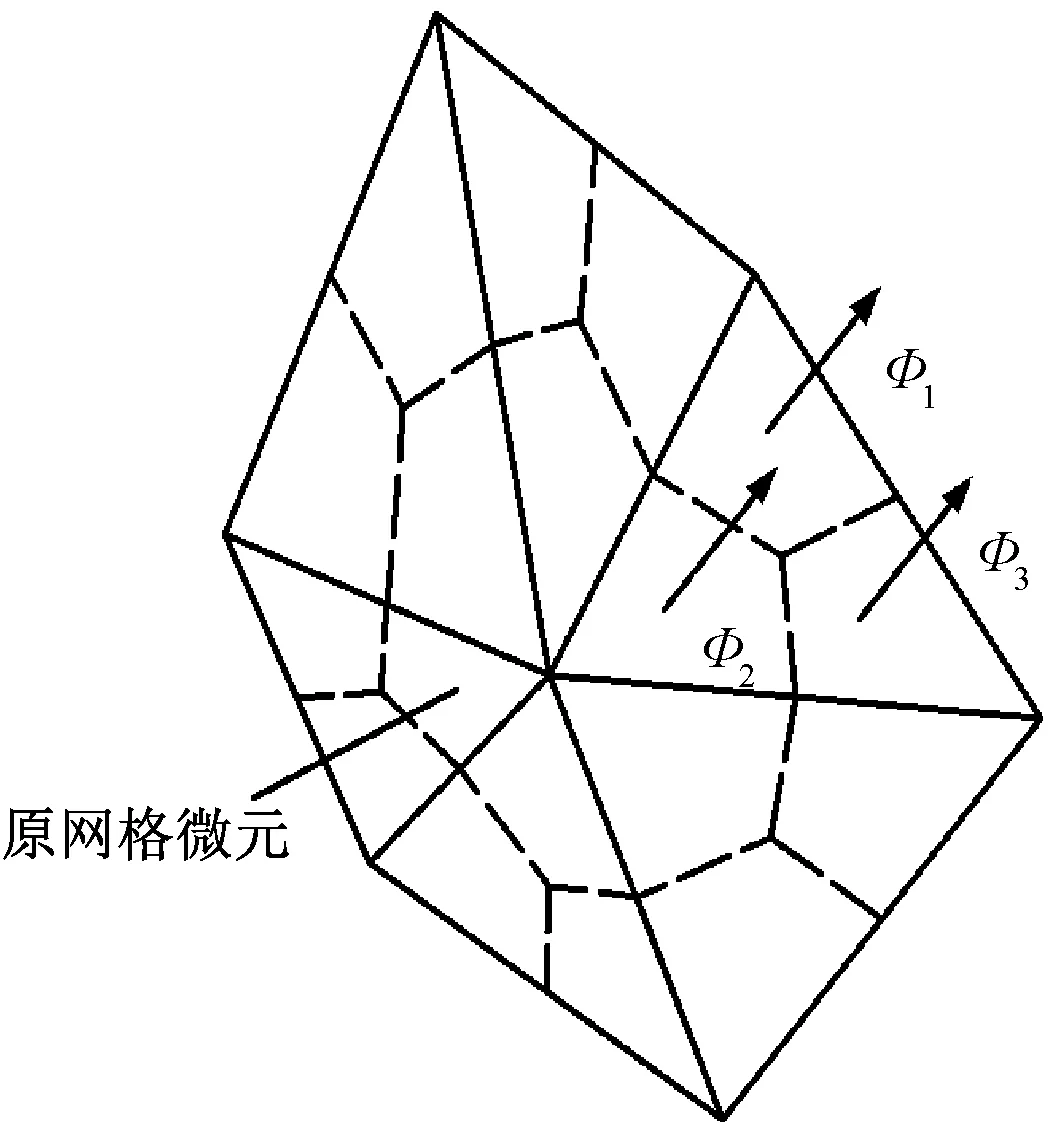
图2 对流散热边界上的原网格与映射网格Fig.2 Primal and dual grids on convection boundary
在对求解域做四面体网格剖分时,文献[6]给出的对流散热边界处理如下:
(4)
式中,Φi(i=1,2,3)为微元热通量;α、A分别为微元散热系数与面积。
式(4)考虑了对流散热边界三角形单元各微元内热通量的差异,但其在编程实现上较为复杂,主要体现在:需要同时修正系数矩阵的对角线元素和非对角线元素,在对非对角线元素的修正中可能出现新的零元素或非零元素。本文将通过各微元内的热通量做平均热通量处理,只对系数矩阵对角线元素做修正,这在编程实现上更为简便,在面网格剖分合理时,其计算准确性可满足工程需要,实现如下:
DO I=1,NUMTRI ! 三角形面单元总数
……
DO J=1,3
NOD=TRI(I,J) !三角形面单元节点编号
DI=ND(NOD) !系数阵对角线元素编号
F(DI)=F(DI)+A*α/3
! F(DI)系数阵对角线元素
Q(NOD)=Q(NOD) +A*α/3
! Q(NOD)节点温度载荷
END DO
END DO
3 模块化程序编制
基于模块化编程思想,本文编写了适用于永磁同步电机三维温度场计算的通用性有限公式法温度场计算程序。
其主程序包含四个模块,分别为数据输入子程序、系数矩阵计算子程序、求解计算子程序与FE格式绘图数据生成子程序。在主程序执行过程中依次调用四个子程序分别实现网格数据与热计算参数导入、系数矩阵的计算、节点温度载荷计算与边界条件处理以及代数方程组ICCG求解、FE格式绘图数据的生成。
为提高程序计算效率,本文在编程实现上一方面将网格数据及热计算参数定义为全局变量以减少主程序调用子程序时参数传递个数和简化子程序间的参数传递过程,另一方面采用合理的程序流程设计以简化相同剖分网格与物性参数、不同热负荷与边界条件时的计算过程。相应计算流程如图3所示。
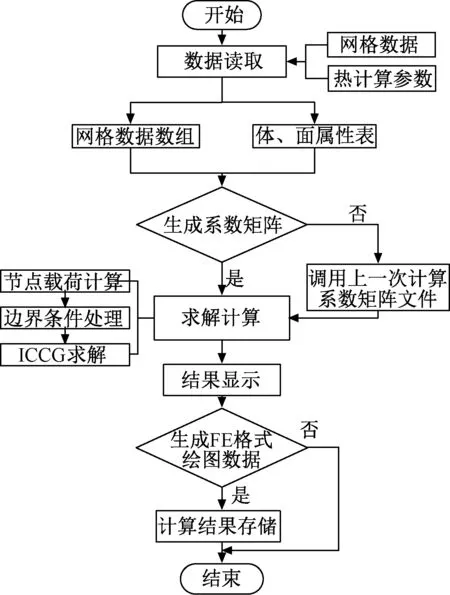
图3 有限公式法温度场计算程序流程图Fig.3 Temperature field calculation flowchart of FFM
4 20kW水冷永磁同步电机温度场计算
4.1 温度场求解模型和热计算参数
为缩减计算规模和计算时间,选取电机八分之一模型作为求解域。电机基本参数如表1所示。

表1 20kW水冷永磁同步电机基本参数
根据电机基本参数确定的20kW水冷永磁同步电机温度场计算模型如图4所示。根据20kW水冷永磁同步电机损耗试验值确定电机各发热部件的损耗和生热率如表2所示。
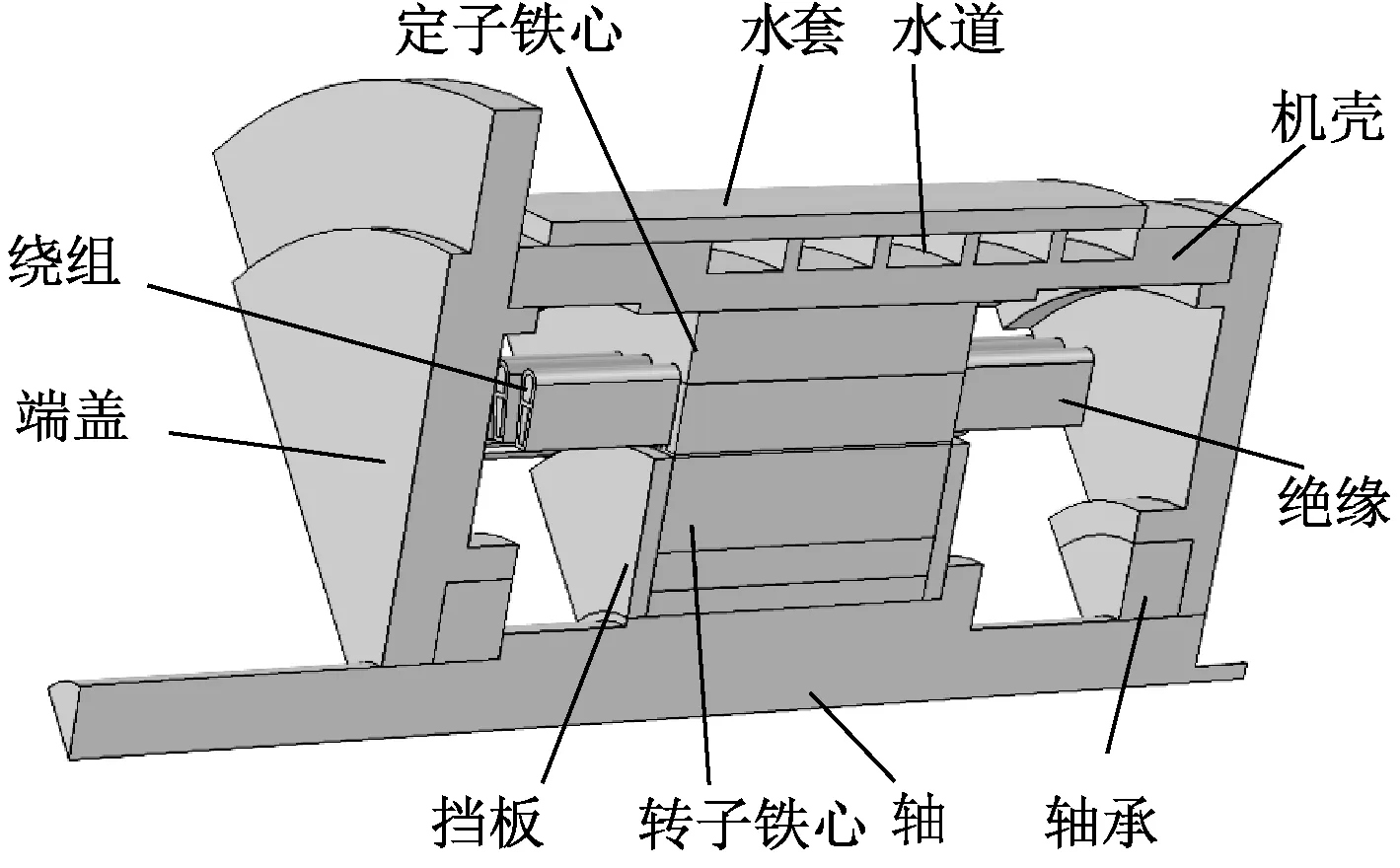
图4 电机求解域模型Fig.4 Physical model of solution region
20kW水冷永磁同步电机在机壳内开有水道,且定子铁心与机壳紧密接触,电机热量主要经水道散热面传递出去。在不考虑水道内冷却水的动能损耗时,根据冷却水道结构参数和水泵供水流量可以折算出水道内冷却水流速,进而确定不同冷却水流速下的水道散热面散热系数,在冷却水处于湍流状态时水道散热系数为[7]:
(5)
式中,α为水道散热面散热系数;u、ρ、ν、λ、cp分别为冷却水的流速、密度、运动粘度、导热系数、定压比热容;dwet为水道当量直径;n为指数常数,流体被加热时取0.4。
定子端面散热系数可计算为[7]:
(6)
式中,α为定子端面散热系数;vd为定子绕组端部的空气流速。由于20kW水冷永磁同步电机转子端部无风刺凸起,端腔空气在定子绕组端部流动缓慢,可近似认为vd=0。
4.2 温度场计算与温升试验
在确定温度场边界条件和各发热部件的生热率后,应用本文所编制的有限公式法温度场计算程序,计算室温20℃、冷却水温20℃、冷却水流速1.975 m/s时的电机温升分布,结果如图5所示。
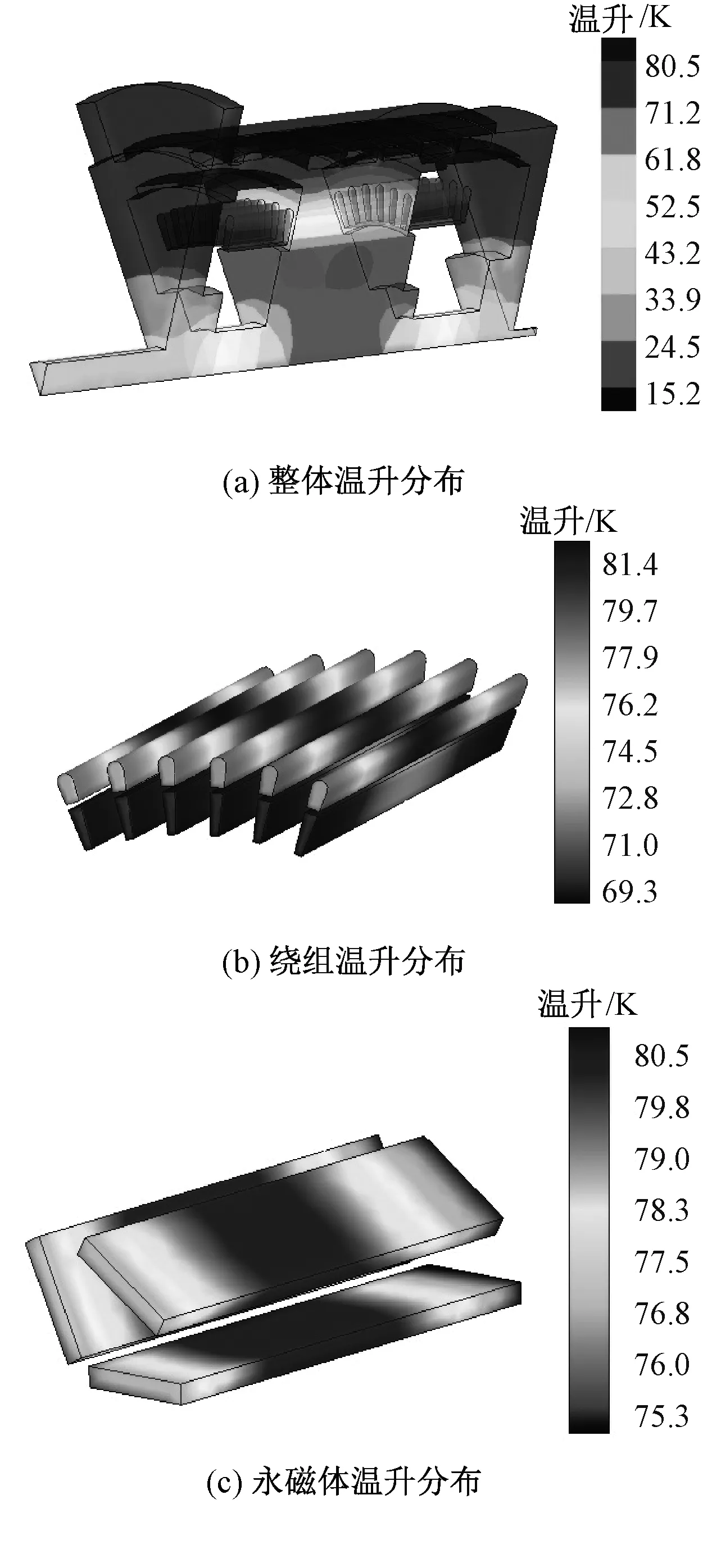
图5 有限公式法计算20kW水冷永磁同步电机温升分布Fig.5 Temperature rise distribution of 20kW water-cooled PMSM calculated by FFM
由图5可知,绕组温升轴向对称分布,上层绕组温升较下层绕组温升高,最高温升点位于上层绕组端部;转子铁心和永磁体温升分布均匀,永磁体平均温升较绕组平均温升高。
本文以室温20℃,水速1.185 m/s、1.58 m/s和1.975 m/s时的绕组温升试验数据来验证有限公式法计算的准确性。图6为该电机温升试验照片,表3为绕组平均温升计算值与试验值对比。
由表3可知,基于有限公式法的绕组温升计算值与试验值误差在3%以内,由此可以得出,本文提出的对流散热边界条件处理方法与编写的模块化计算程序是正确的。

图6 20kW水冷永磁同步电机温升试验Fig.6 Temperature rise test of 20kW water-cooled PMSM
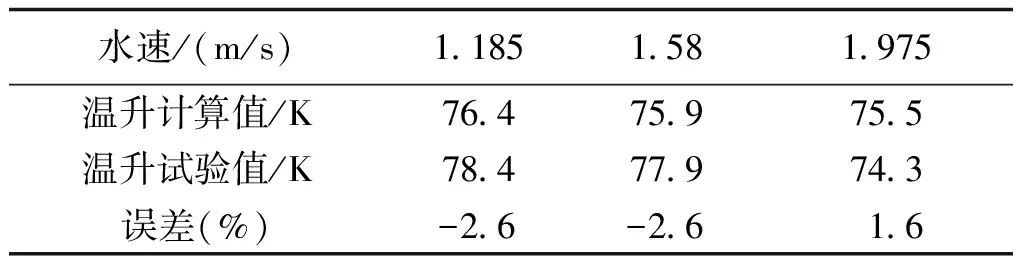
水速/(m/s)11851581975温升计算值/K764759755温升试验值/K784779743误差(%)-26-2616
4.3 冷却水流速、冷却温度与电机温升关系研究
水冷永磁同步电机的温升与冷却水流速、冷却水温密切相关[8,9],为研究不同冷却水流速和冷却水温对水冷永磁同步电机温升分布的影响,本文对冷却水流速为0.1m/s、0.185 m/s、0.5 m/s、0.79 m/s、1.185 m/s、1.58 m/s和1.975 m/s,冷却水温为10℃、15℃、20℃、25℃和30℃下的水冷永磁同步电机温度场进行了分析。
表4为应用有限公式法计算得到的绕组、永磁体在不同冷却水流速、冷却水温下的平均温升,图7为依据表4中计算数据绘出的永磁体平均温升与冷却水流速、冷却水温的关系曲线。
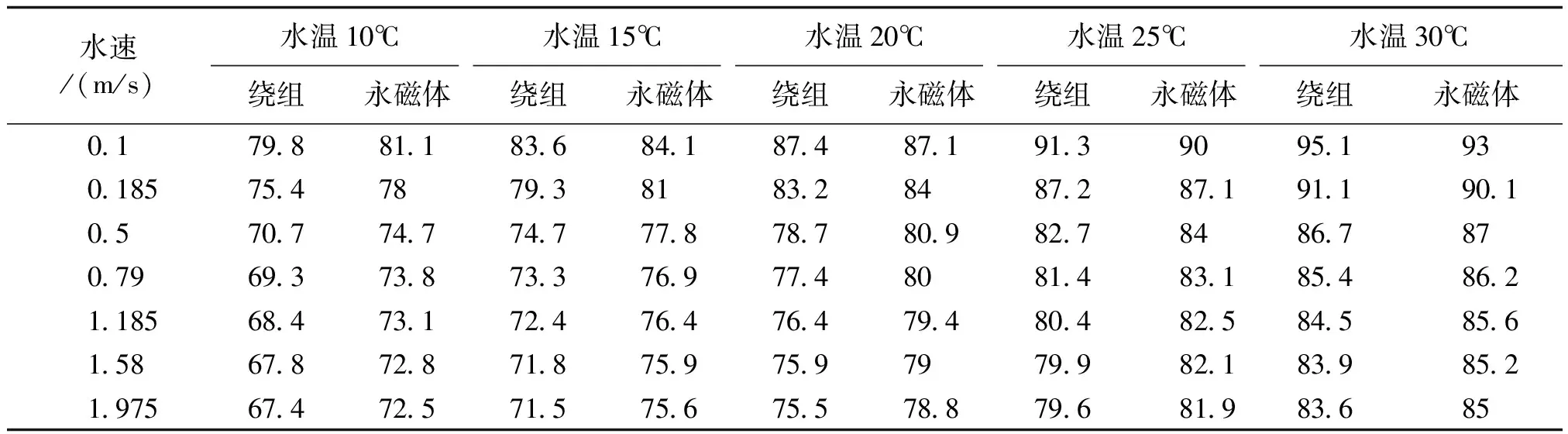
表4 不同冷却水流速、冷却水温下电机平均温升计算值
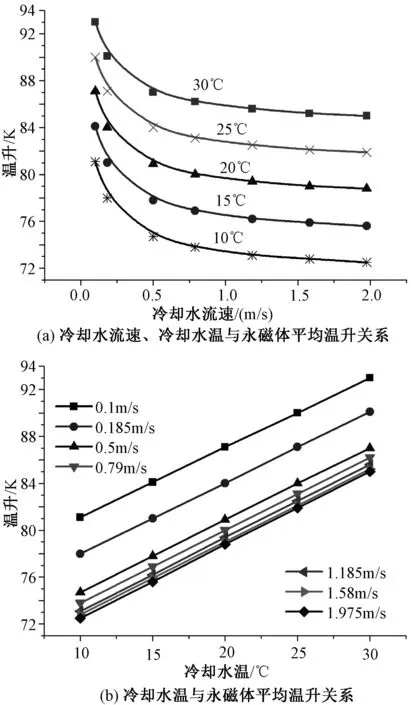
图7 冷却水流速、冷却水温与永磁体温升关系Fig.7 Relationship of water flow rate and temperature vs. temperature rise of permanent magnet
结合表4中计算数据可知,绕组平均温升与冷却水流速、冷却水温的关系与图7相类似,故这里只绘出了永磁体平均温升与冷却水流速、冷却水温的关系曲线。
根据流体力学理论,当水道冷却水流动特征量雷诺数Re<2200时,流体处于层流状态;当2200
(7)
式中,u、L分别为特征速度和特征长度。可依据式(7)确定20kW水冷永磁同步电机水道临界水流速为v1=0.185m/s,v2=0.83m/s。其中,v1为由层流到过渡区的临界水流速,v2为过渡区到湍流的临界水流速。
由表4及图7可知,在冷却水流速v
为验证本文所编制的基于有限公式法温度场计算程序的正确性,在同一网格相同热参数加载下应用商业有限元软件计算得到的冷却水流速、冷却水温与永磁体平均温升关系如图8所示。
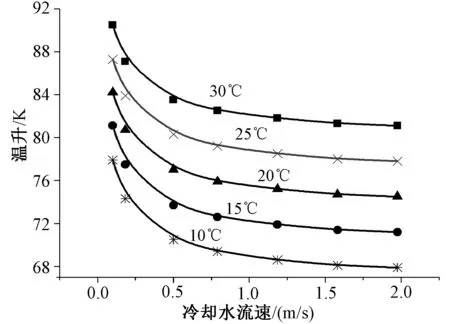
图8 有限元法计算冷却水流速、水温与永磁体温升关系Fig.8 Relationship of water flow rate and temperature vs. temperature rise of permanent magnet calculated by FEM
结合图7、图8以及表4中的温升计算值可知,在相同网格、热参数加载一致的情形下,基于有限公式法与有限元法计算的永磁体平均温升相差在5K以内,其误差来源与边界条件的处理有关,原因在于本文基于映射网格体的对流散热边界处理未考虑散热边界上温度梯度对电机表面散热的影响,但其在编程实现上简便且能满足工程计算的要求。
5 结论
本文在建立有限公式法温度场模型的基础上,讨论了有限公式法对流散热边界的处理和编程实现,应用编写的模块化程序对一台20kW水冷永磁同步电机温度场进行了计算,结论如下:
(1)采用的简化对流散热边界处理在编程实现上具有简单、实用的特点,通过与电机温升试验值、同一网格相同热计算参数加载下有限元计算值对比,验证了对流散热边界处理的正确性。
(2)提出的程序设计流程是切实可行的,所编写的模块化程序在永磁同步电机三维温度场计算上具有通用性好、计算效率高、可移植性好的特点。
[1] Piergiorgio Alotto, Fabio Freschi, Maurizio Repetto. Multiphysics problem via the cell method: the role of tonti diagrams [J]. IEEE Transactions on Magnetics, 2010, 46(8): 2959-2962.
[2] Marco Bullo, Fabrizio Duhiero, Massimo Guarnieri, et al. A 2-D formulation for eddy current anisotropic problems with the cell method [J]. IEEE Transactions on Magnetics, 2005, 41(5): 1368-1371.
[3] Marco Bullo, Valentina D’Ambrosio, Fabrizio Dughiero, et al. A 3-D cell method formulation for coupled electric and thermal problems [J]. IEEE Transactions on Magnetics, 2007, 43(4): 1197-1200.
[4] 严登俊, 刘瑞芳, 朱长江 (Yan Dengjun, Liu Ruifang, Zhu Changjiang). 电机电磁场的有限公式计算技术(Calculation technology of finite formulation for electromagnetic field in electrical machine) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2008, 28(6): 110-115.
[5] 严登俊, 刘瑞芳, 李伟(Yan Dengjun, Liu Ruifang, Li Wei). 有限公式法二维涡流场计算技术及其在电机集肤效应计算中的应用(Finite formulation computation technology for 2D eddy current field and application for skin effect in squirrel cage motor)[J]. 中国电机工程学报 (Proceedings of the CSEE), 2008, 28(9): 133-138.
[6] Piergiorgio Alotto, Marco Bullo, Massimo Guarnieri, et al. A coupled thermo-electromagnetic formulation based on the cell method [J]. IEEE Transactions on Magnetics, 2008, 44(6): 702-705.
[7] 魏永田, 孟大伟, 温嘉斌 (Wei Yongtian, Meng Dawei, Wen Jiabin). 电机内热交换 (Motor heat exchange) [M]. 北京:机械工业出版社 (Beijing: China Machine Press), 1998.
[8] 陈丽香, 程文 (Chen Lixiang, Cheng Wen). 永磁力矩电动机流体场分析与温升计算 (Fluid field analysis and temperature calculation for permanent magnet torque motor) [J]. 微特电机 (Small & Special Electrical Machines), 2015, 45(1): 13-17.
[9] 温嘉斌, 许明宇 (Wen Jiabin, Xu Mingyu). 防爆型水冷电机内换热与温度场计算(Calculation on heat exchange and temperature field in water-cooled explosion-proof motor) [J]. 电机与控制学报 (Electric Machine and Control), 2009,13(3): 393-397.
3D temperature field analysis of water-cooled permanent magnet synchronous motor based on finite formulation method
TONG Wen-ming, SHU Sheng-lang, ZHU Gao-jia, CHENG Xue-bin
(National Engineering Research Center for Rare-earth Permanent Magnet Machines, Shenyang University of Technology, Shenyang 110870, China)
Finite formulation method(FFM)is a new discrete numerical method which complies with the laws of physics and uses global variable defined on geometry construction of two nested grids to obtain discrete equations. On the basis of the finite formulation method of temperature field mathematical model, the paper discusses the implementation of grid-based mapping convection boundary treatment and programming, and gives the basic idea of designing calculation program. Finally, take a 20kW water-cooled permanent magnet motor 3D temperature field as an example, it analyzes the relationship of the cooling water flow rate and cooling temperature and motor temperature distribution, meanwhile, the values of temperature rise calculated by Finite Element Method(FEM)under the same grid and temperature test verified the accuracy and reliability of the program.
finite formulation method; temperature field; boundary condition; permanent magnet synchronous motor; numerical calculation
2015-08-31
国家自然科学基金(51307111)、 国家科技支撑计划(2013BAE08B00)、 辽宁省教育厅科学技术研究(L2013049)资助项目
佟文明(1984-), 男, 辽宁籍, 副教授, 硕士生导师, 博士, 研究方向为特种电机及其控制; 舒圣浪(1990-), 男, 江西籍, 硕士研究生, 研究方向为永磁电机多物理场仿真与分析。
TM315
A
1003-3076(2016)07-0036-06
