运用动态定位分析解决中考运动问题

☉江苏省太仓市第一中学　李　婧



运用动态定位分析解决中考运动问题

☉江苏省太仓市第一中学李婧

运动类问题作为中考中的一类常见的压轴问题，具有变化多、思维要求高、区分度好的特点，一直受到中考命题者的欢迎和喜爱.在解决此类问题的时候，需要变动为静，对动态问题进行定位分析，画出相关的静态图形，确定相关的等量关系，从而有效地进行解决.下面笔者以2015年中考运动试题为例，加以分析，供大家欣赏与研究.

一、基本图形为模板，考查迁移能力

此类问题的图形是学生经常见到的，但是进行了一系列的补充，在原问题的基础上就有了新意.学生在尝试解决此类问题时，容易从原本的记忆库中找到对应的图形，从而便于找到问题的突破口和解决途径.

例1（2015年山东聊城）如图1，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3.动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1.25个单位长度的速度，沿OB向终点B移动.当两个动点运动了x秒（0＜x＜4）时，解答下列问题：

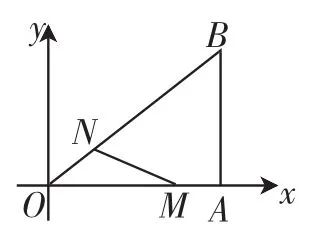
图1

（1）求点N的坐标（用含x的代数式表示）.

（2）设△OMN的面积是S，求S与x之间的函数表达式.当x为何值时，S有最大值？最大值是多少？

（3）在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由.

分析：（1）由勾股定理求出OB=5，作NP⊥OA于点P，则NP∥AB，得出△OPN∽△OAB，得出比例式，求出OP、PN，即可得出点N的坐标.

（2）由三角形的面积公式得出S是x的二次函数，即可得出S的最大值.

（3）分两种情况：①若∠OMN=90°，则MN∥AB，由平行线得出△OMN∽△OAB，得出比例式；②若∠ONM= 90°，则∠ONM=∠OAB，证出△OMN∽△OBA，得出比例式.

点评：本题是相似形综合题目，图形较为常见，属于学生熟悉的题型，考查了相似三角形的判定与性质、勾股定理、坐标与图形特征、直角三角形的性质、三角形面积的计算、求二次函数的解析式及最值等知识；本题难度较大，综合性强，特别是第（3）问，需要进行分类讨论，通过证明三角形相似才能得出结果.

二、猜想与归纳先行，考查学生思维能力

此类问题首先要根据问题情境进行一定的猜想与归纳，然后对猜想的问题进行有效的验证与解决，对学生的推理和解决问题的能力提出了较高的要求.

例2（2015年浙江湖州）在直角坐标系xOy中，O为坐标原点，线段AB的两个端点A（0，2），B（1，0）分别在y轴和x轴的正半轴上，C为线段AB的中点，现将线段BA绕点B按顺时针方向旋转90°得到线段BD，抛物线y=ax2+ bx+c（a≠0）经过点D.

①求点D的坐标及该抛物线的解析式；

②连接CD，问：在抛物线上是否存在点P，使得∠POB与∠BCD互余？若存在，请求出所有满足条件的点P的坐标；若不存在，请说明理由.

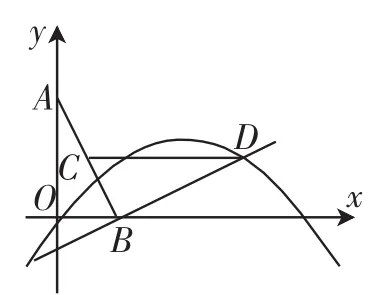
图2

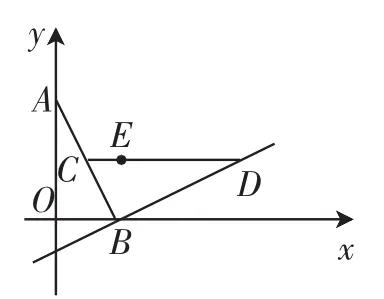
图3

（2）如图3，若该抛物线y=ax2+bx+c（a≠0）经过点E（1，1），点Q在抛物线上，且满足∠QOB与∠BCD互余，若符合条件的Q点有4个，请直接写出a的取值范围.

分析：（1）①过点D作DF⊥x轴于点F，可证△AOB与△BFD全等，求得D点的坐标，把a=-与点D的坐标代入抛物线即可求抛物线的解析式.②由C、D两点的纵坐标都为1可知CD∥x轴，所以∠BCD=∠ABO.又因∠BAO与∠BCD互余，若要使得∠POB与∠BCD互余，则需满足∠POB=∠BAO.分两种情况：第一种情况，当点P在x轴上方时；第二种情况，当点P在x轴下方时，利用同样的方法可求点P的坐标.

（2）抛物线y=ax2+bx+c过点E、D，代入可得，分两种情况：①当抛物线y=ax2+bx+c开口向下时，满足∠QOB与∠BCD互余且符合条件的Q点有4个，②当抛物线y=ax2+ bx+c开口向上时，满足∠QOB与∠BCD互余且符合条件的Q点有4个，点Q在x轴的上、下方各有两个，当点Q在x轴的上方时，直线OQ与抛物线y=ax2+bx+c有两个交点，符合条件的点Q有两个.当点Q在x轴的下方时，直线OQ必须与抛物线y=ax2+bx+c有两个交点，符合条件的点Q才有两个.

点评：对于存在性问题的解答，需要学生首先对问题进行分析和猜想，然后进行适当的分类讨论，从而完整地解决问题.

三、运动中找到关键位置，静态中定位动态问题

几何问题的完美解决，需要在解题中画出相对应的图形，在静态的过程中解决动态的问题，于是定位、作图、解决成为解题的关键.

例3（2015年四川自贡）在△ABC中，AB=AC=5， cos∠ABC=，将△ABC绕点C顺时针旋转，得到△A1B1C.

（1）如图4，当点B1在线段BA的延长线上时.①求证：BB1∥CA；②求△AB1C的面积.

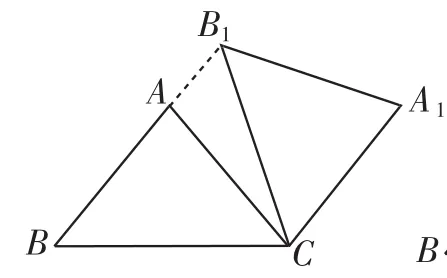
图4

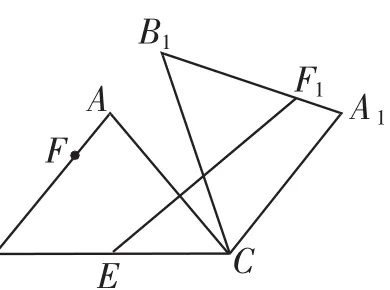
图5

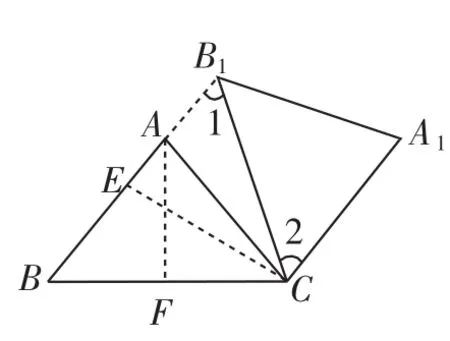
图6

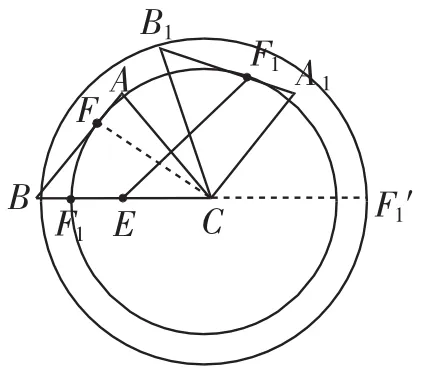
图7

（2）如图5，E是BC的中点，F为线段AB上的动点，在△ABC绕点C顺时针旋转过程中，点F的对应点是F1，求线段EF1长度的最大值与最小值的差.

分析：如图6，要使BB1∥CA1，根据本题的条件通过这两线所截得的内错角∠1=∠2来证得.根据AB=AC可以得出∠B=∠ACB，根据旋转的特征可以得出B1C=BC，所以∠1=∠B，而∠2=∠ACB（旋转角相等），所以∠1= ∠2.②求△AB1C的面积可以把AB1作为底边，其高在B1A的延长线上，恰好落在等腰△ABC的边AB上；在等腰△ABC和△BB1C中，根据等腰三角形的性质、三角函数及勾股定理可以求出AB、BB1、CE，而AB1=BB1-AB，△AB1C的面积可以通过AB1×CE求出.

（2）如图7，点C到AB的垂线段最短，过点C作CF⊥AB于点F；点F的对应点是F1，若以点C为圆心、CF为半径画圆，EF1有最小值；根据（1）的CA=AB=5和求出的BC= 6，当点F在线段AB上移到端点A时CA最长，此时其对应点F′移动到A1时CA1也就最长；如图7，以点C为圆心、BC为半径画圆，EF1有最大值，EF1有最小值和最大值都可以利用同圆的半径相等和在圆的同一条直径上来获得解决.

点评：这是2015年中考命题中较为少见的优质试题，背景非常简单，但对思维的要求却比较高，只有在运动中准确定位，才是解决此类问题的关键所在.

四、变化中进行动态分析，解决几何变式问题

几何问题的运动，是近年来中考非常关注的考查点之一，在此类问题的考查过程中，变式研究成为命题的一个常见的方向.

例4（2015年湖南岳阳）已知直线m∥n，C是直线m上一点，D是直线n上一点，CD与直线m、n不垂直，P为线段CD的中点.

（1）操作发现：直线l⊥m，l⊥n，垂足分别为A、B，当点A与点C重合时（如图8所示），连接PB，请直接写出线段PA与PB的数量关系：____________ .

（2）猜想证明：在图①的情况下，把直线l向上平移到如图9的位置，试问（1）中的PA与PB的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由.

（3）延伸探究：在图9的情况下，把直线l绕点A旋转，使得∠APB=90°（如图10所示），若两平行线m、n之间的距离为2k.求证：PA·PB=k·AB.

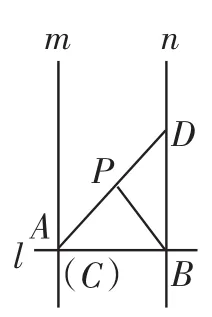
图8

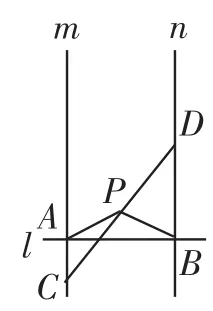
图9

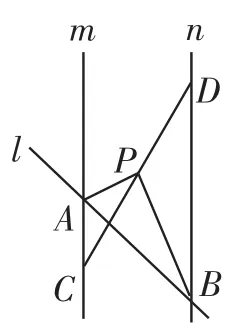
图10

分析：（1）根据三角形CBD是直角三角形，而且P为线段CD的中点，应用直角三角形的性质，可得PA=PB，据此解答即可.（2）过点C作CE⊥n于点E，连接PE，然后分别判断出PC=PE、∠PCA=∠PEB、AC=BE；然后根据全等三角形判定的方法判断出PA=PB成立.（3）首先，延长AP交直线n于点F，作AE⊥BD于点E，然后，根据相似三角形判定的方法可判断出AF·BP=AE·BF，再由AF=2PA，AE= 2k，BF=AB，可得2PA·PB=2k·AB，所以PA·PB=k·AB.

点评：此题为几何变换综合题，几何变换本质上就是图形的运动.本题考查了分类讨论思想的应用、数形结合思想的应用、从图像中获取信息，并能利用获取的信息解答相应问题的能力.另外，此题还考查了全等三角形的判定和性质的应用，以及相似三角形的判定和性质的应用，是一个非常不错的综合问题.

综上所述，运动问题与一般试题相比，问题的立意更高，综合性更强，考查的知识点更加密集，对学生的思维要求也相对更高.在解决此类问题时，需要关注运动中的不变要素，化“运动”为“静止”，在运动中定位搜寻解决问题的相关条件.当然，在解决问题的同时，关注学生作图能力的培养也非常重要，综合问题只有把正确的图形作出来，才有可能完全解决一类问题，从而在解决问题的过程中也能有所收获，真正做到入宝山而寻宝归的最佳效果.

参考文献：

1.石树伟.为了改善学生的学而设计［J］.中国数学教育（初中版），2013（1-2）.

2.朱宸材，王宇峰.例谈数学变式教学对于学生思维能力的培养［J］.上海中学数学，2015（1-2）.