一道几何压轴题的解法探究及亮点赏析——2016年北京市海淀区初三第一学期期末试题第28题
2016-05-03北京市中关村中学杨爱青
☉北京市中关村中学 杨爱青
一道几何压轴题的解法探究及亮点赏析——2016年北京市海淀区初三第一学期期末试题第28题
☉北京市中关村中学杨爱青
一、原题呈现
题目(1)如图1,△ABC中,∠C=90°,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为_______;
(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.
①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);
②在图3中补全图形,求∠EOF的度数;
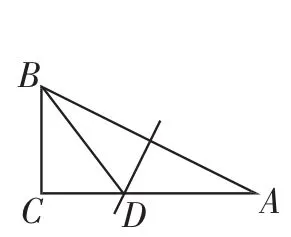
图1
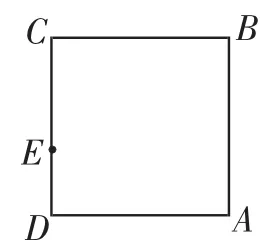
图2
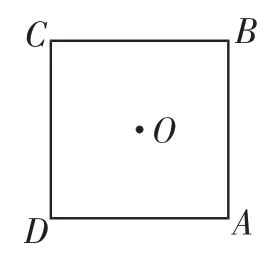
图3
二、解法探究
几何题,我们首先看到的就是它的图,题中的图2、图3给出了正方形,图3还给出了正方形的中心,感觉很熟悉,很亲切,正方形的性质无外乎两点,第一点是旋转,也就是绕着它的中心旋转90°、180°、270°与自身重合,第二点就是轴对称,它有四条对称轴.图1说的是什么?它跟正方形有什么联系?带着这个问题我们一起走进这道题.
先解决第(1)问、第(2)问的①.
根据垂直平分线的性质可以得到AD=BD,这样就有BD+CD=AD+CD=AC,因此△BCD的周长等于AC+BC,等于3.
了解了图1,但是它跟图2、图3中的正方形有什么联系还不知道,继续往下看第(2)问的①.
看我们要作的△EDF,它是直角三角形,其周长一定,为正方形的边长,一条直角边DE图中已给定,它的斜边EF与另一条直角边DF的和应该等于CE的长;再看图1中的△BCD,也是直角三角形,它的周长为3,一条直角边BC的长为1,另一条直角边CD与斜边BD的和为2.
我们完全可以仿照图1解决△EDF的作图问题.能够想到△EDF的作图与图1有联系,并且能够正确建立这个联系,是解决这一问的关键.题目中明确了:“F为AD边上一点”,仿照图1,把斜边EF与直角边DF的和CE,搬到DG处(作AF=CE或AG=DE),连接EG,作EG的中垂线,EG的中垂线与DG的交点即为点F,如图4所示.
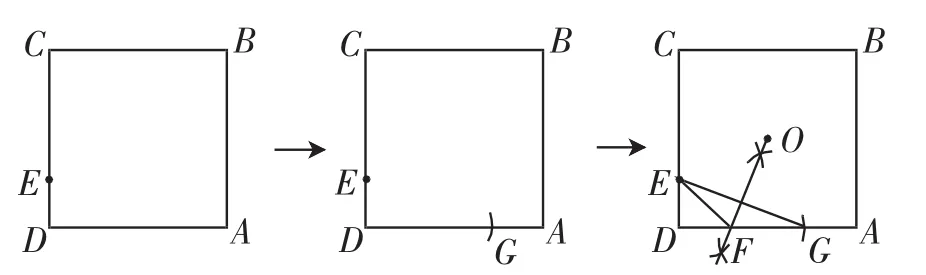
图4
然后解决第(2)问的②.
方法1:由学生熟知的“基本图形”迁移得到.
有了前面作图的铺垫,尝试度量∠EOF的度数,发现是45°,联想到图5(学生对这个图非常熟悉),把“△EDF的周长等于AD的长”这个条件转化为“△EDF的周长=DH+DG”,进而转化为“EF=FH+EG”,如图6所示,然后按照“成题”的思路解决问题就可以了.
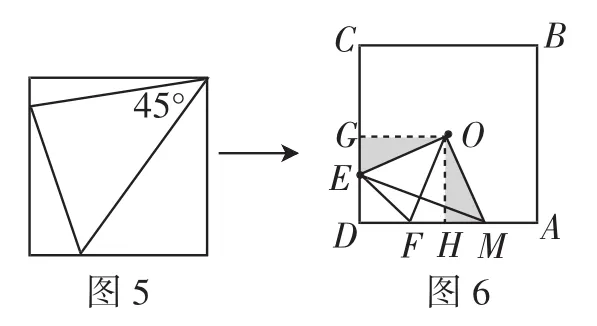
方法2:由△EDF的作图方法迁移得到.
如图7,在AD上截取AG,使得AG=DE,连接OA、OD、OG.由△ODE≌△OAG,可以证明∠EOG=90°,OE=OG,由“△EDF的周长等于AD的长”,AG=DE,容易得到EF= FG,再通过△OEF≌△OGF得到∠EOF=45°,也可以通过OF为EG的中垂线和等腰三角形的性质得到∠EOF=45°.

图7
方法3:由图1和图2的联系“勾股弦图”联想得到.
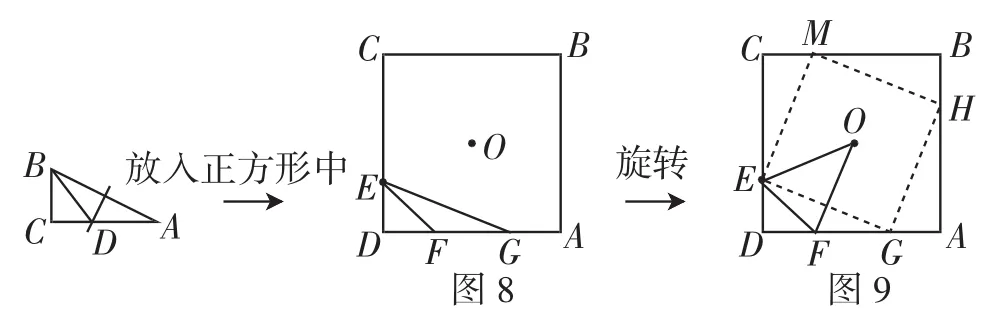
图8可以看做是将图1放入正方形ABCD中得到的,将图8中的△GED绕点O逆时针旋转90°、180°、270°,就得到了我们熟悉的“弦图”,如图9所示,借助这个“弦图”可以求得∠EOF=45°.借助“弦图”求∠EOF的度数,应特别注意书写规范,首先可以借助全等证明四边形EGHM为正方形,然后借助平行四边形BEDH的对角线互相平分,证明O也是正方形EGHM的中心,得到∠EOG=90°,进而得到∠EOF=45°.
再解决第(2)问的③.
第一类方法:利用相似.
如图10,由AF、CE、OF、OE,我们顺藤摸瓜找到了△COE和△AFO,易知∠1=∠2=∠EOF=45°,图11是图10中的一部分,这个图我们熟悉吗?
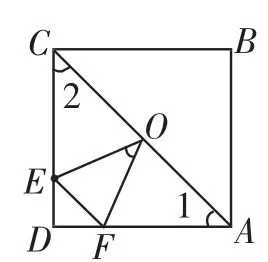
图10

图11
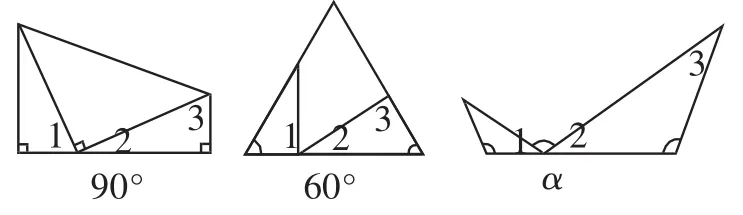
图12
如图12,∠1+∠2=180°-α,∠3+∠2=180°-α,所以∠1=∠3.
方法3:如图10,不难证明,∠CEO=∠FEO,∠EFO= ∠AFO,因此,△COE∽△OFE∽△AFO,所以OE2=EF· CE,OF2=EF·AF,也可得到
第二类方法:利用勾股定理计算得到.
方法4:利用勾股定理构造方程求解.
如图6,设OE=x,则正方形边长为9k+x,由AF=8k可知DF=k+x,EF=8k-x,由勾股定理可得x2+(k+x)2=(8k-x)2,求得DE=3k,DF=4k,EF=5k,所以AD=12k,进而得到OG= OH=6k,GE=3k,FH=2k,再用勾股定理算出OF=2OE=3,得到
方法5:利用“勾股弦图”求解.
如图13,设DF=CJ=BL=AK=b,DE=a,EF=c,则AF=a+c,a2+b2=c2.由FK2=2OF2=AF2+AK2=b2+(a+c)2,可得OF2=c·AF.
同理,如图9,DE=CM=BH=AG=a,则DG=CE=b+c,a2+b2=c2.由EG2=2OE2=DE2+DG2=a2+(b+c)2可得OE2=c·CE.
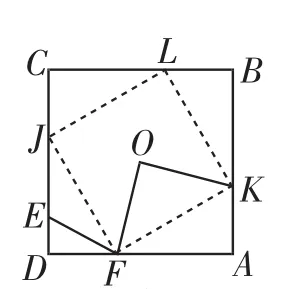
图13
最后是解题后对题目的反思.
思考1:图中周长等于正方形边长的直角△EDF唯一吗?如果不唯一,有多少个?点E的运动范围(DE的取值范围)是什么?
思考2:在点E的运动过程中,有∠EOF=45°,EO、FO分别为∠CEF、∠AFE的平分线,,这些不变量或不变的关系,还有其他的吗?
由△COE∽△AFO,还可以得到AF·CE=AO2=AB2,这个结论又说明了什么?它是不是说明在“△EDF的周长等于正方形的一边长”的条件下,如图14,矩形BGMH的面积是个定值,始终为正方形ABCD面积的一半?这个结论的证明,还有其他方法吗?
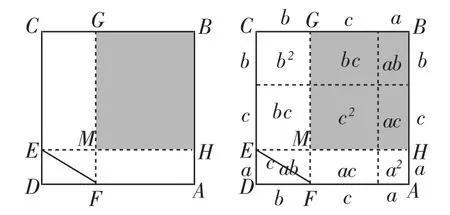
图14
我们老师个人的能力是有限的,只要您把分析图形的方法教给学生,然后把具体地分析这个图的任务放手交给学生,相信学生一定会给您一个大大的惊喜.
三、亮点赏析
1.问题引导探究,突出研究问题的基本方法和基本活动经验的考查
本题第(2)问的解答过程就是一个典型的数学问题的探究过程,它很好地体现了研究几何问题的基本套路和方法.第①小问,在图2中作出△DEF,第②小问,在图3中补全图形并求∠EOF的度数,第③小问,应用第②小问的结论解决问题,这样的设置,使学生在解题的过程中,经历了一个动手操作(作图)——猜想结论(合情推理)——证明结论(演绎推理)——应用结论的过程,并通过这样的过程,积累如何去研究问题的经验.本题中,对“∠EOF的度数”这一不变量的认知,是建立在学生自己动手作图、度量猜想的基础上的,它具有不可替代的直观性,对学生认识图形结构,理解问题、解决问题有着积极的意义.
2.设问层层递进,注重数学思想方法的考查
设问层层递进,这里有两层含义,一是指试题的几个问题逐层深入,前一个问题是后一个问题的铺垫.第(1)问是为第(2)问的第①小问做铺垫,△EDF的作图可以仿照图1来完成;而第(2)问的第②小问求∠EOF的度数,无论是得出结论还是证明结论的方法,都离不开△EDF的作图;第(2)问的第③小问的解答,是建立在前面结论的基础上的.二是难度的递进.第(1)问,考查线段的中垂线的性质,对学生来说比较容易;第(2)的第①小问的作图,依赖于在阅读理解的基础上,建立△EDF的作图与图1的联系,考查的是对图形的迁移能力,相比第(1)问要有些难度;第(2)的第②、③小问,更是综合了三角形的全等和相似、正方形的性质、勾股定理、旋转等知识,考查学生分析解决综合问题的能力,完全答对实属不易.本题难度层次非常清楚,体现了较好的区分度.
本题着重数学思想方法的考查.建立图1与△EDF作图之间的联系,然后运用类比的思想方法解决△EDF的作图问题;第(2)问的第③小问,利用勾股定理构造方程求解,考查了方程与建模的思想;第(2)问的第②小问,由于图2中的点E为一给定的特殊位置,由这一特殊位置度量出∠EOF的度数去猜想一般性的结论,并从第①小问的作图中受到启发,得到求∠EOF度数的方法(方法2),这里渗透了特殊化这一探究问题的方法;题目解决的过程中,始终都没离开化归、变换的思想方法.
3.打破思维定式,突出对核心内容、数学本质的考查
由前面的解法探究可知,本题主要涉及三个“基本图形”,如图15所示,它们有的来自我们的教材,有的是教材中例习题的变式,三个基本图形链接精巧,环环相扣,浑然一体.对这些基本图形和相应的结论,学生都非常熟悉,可仍感觉这道题并不容易,这是由于题目的考查角度比较新颖,不是记住一些图形,记住图形中的一些结论,生搬硬套就可以解决问题的,只有对这些图形的结构、图形之间的联系有比较透彻的理解,才能正确解答,25.5%的得分率也说明了这一点.考查的核心内容不变,考查的角度新颖独特,打破思维定式,多思少算是本题的特色之一,也是北京中考改革的一个方向.
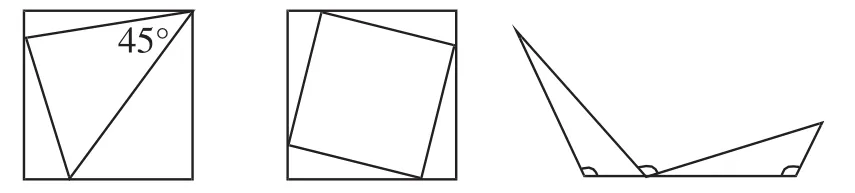
图15
参考文献:
1.杨春鸟.一道中考几何压轴题的解法探究和亮点赏析[J].中学数学(下),2015(5).
