“数学哲学”原理在解题中“给力”
2016-05-03江苏省南京市雨花台区教师发展中心刘春书
☉江苏省南京市雨花台区教师发展中心 刘春书
“数学哲学”原理在解题中“给力”
☉江苏省南京市雨花台区教师发展中心刘春书
一、引言
一道题目的评析过程,可谓“一波三折”,学生思路完全缺失,意外不断.尽管不断启发,但始终未达预设,反而越走越远.这一过程触发了从猜想到证明的一系列反思,最后演化为对解决数学问题具有指导意义的三个“数学哲学”原理.其中“一般问题特殊化”指对变化的问题可以利用特殊位置或特殊值进行猜想,寻觅问题本质;“量变产生质定”指通过变量的表示、转化,最终消去变量或求出变量,从而确定本质;“以定研变得不变”指从条件入手分析,寻找定的元素,再以此为突破口研究变化的量或位置,最终得出定量或量与量之间不变的关系.这三个理论统称为“数学哲学”原理.
二、评析简录
问题1:如图1,在矩形ABCD中,P为AD边上的一个动点,PE、PF分别垂直于AC、BD,垂足为E、F,若AB=3,BC=4,请问:在点P运动的过程中PE+PF为多少?
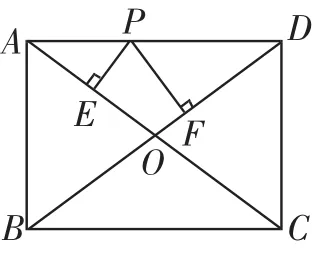
图1
出示本题,学生无思路,给启发:PE与PF是什么?能想到什么?要好好利用这一条件,几分钟后,学生仍旧无法打开思路,于是回忆一道曾经做过的题目.
问题2:如图2,已知等边△ABC的边长为2,三角形内有一点P,PE、PF、PG分别垂直AB、BC、AC,垂足分别为E、F、G,求PE+PF+PG的长度.
这是一道到用面积关系解决的经典题,学生很快给出了解题思路.请大家再思考问题1,本以为即将柳暗花明又一村,可困境依旧.
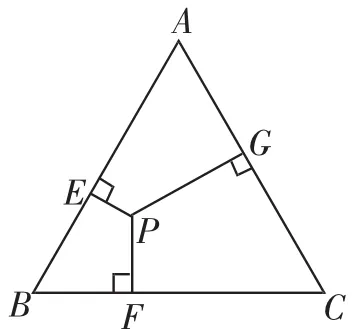
图2
生1:如图3,将点P运动到点A,此时P、A、E三点重合,这样PE+PF=0+PF,然后在△ABD中利用面积求出PF,即,求得PF=
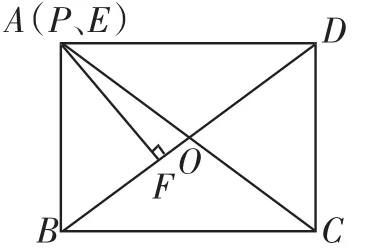
图3
师:“一般问题特殊化”分析,这是极限思维,这样的分析只能用于猜想,不能作为说理.同学们遇到问题要好好分析条件,思考由条件能够联想到什么?
生2:△AEP∽△ADC∽△DFP.
笔者惊呆了,这与自己的预设越来越远,怎么办?再次有点沉不住气了,就在笔者左右为难之时,学生3突然举手.
生3:可以利用△AEP∽△ADC∽△DFP.
师:你说什么?那你说说怎么做?(这完全出乎自己的意料,好在平时具有相信学生和依靠学生的习惯)
其实本解法是在学生2的启发下,对问题进行了一次定“质”的研究,即变中不变,点P在运动的过程中,△AEP与△DFP的大小变,但其形状不变,则与定△ADC存在相似的关系.立刻在笔者的脑海中产生这样的一个巨大的问号:是不是所有问题的解决都需要进行定质的思考?也许这就是学生不能解决问题的根源所在.于是试着从这一角度进行再次引导.
师:无论点P怎么运动,有无其他的定量或量与量之间固定的关系?
2分钟后,许多学生陆续有了正确的思路.
生4:如图4,无论点P怎么运动,△AOD的面积不变,△AOP与△DOP的面积和等于△AOD的面积.
在矩形ABCD中,连接PO,S矩形ABCD=AB×BC=3×4=12.
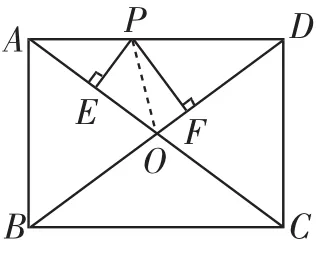
图4
三、提炼反思
首先,一般问题特殊化.数学、哲学、数学哲学,三者的关系从普遍、一般再到特殊,数学哲学为数学指引方向.结合本题的突破过程不难发现数学哲学在此发挥的作用,即在不知道PE与PF的和为多少时,运用了极限思维,就是一般问题特殊化,从而猜出PE与PF的和为.这正是一次数学哲学的应用,世间万物具有普遍性、一般性,同时具有其特殊性,往往特殊性就是研究普遍性与一般性的突破口.大凡科学研究都需经历一个从特殊去猜想,从一般去实验、推理的过程.这一节课的分析过程正是一次“数学哲学”最生动的体现.应当引导学生利用这一数学哲学原理去解决数学问题.
其次,量变产生质定.其实在数学问题解决的过程中,就应用到这一数学哲学.质为万事万物的本质,量就是事物的变化中的数量.也就是从量的角度去分析、推理、转化,最终得到质的确定.数学是研究量与量的关系的一门学科,量分定量与变量,既要研究常量,更要研究变量,对于不确定量与变量的研究,自然想到字母,因为字母具有代表性、一般性、普遍性.比如,从相似设AP长为x,经过对应边成比例,分别用x表示出PE与PF,再将PE与PF相加,消去变量x,最终PE与PF和的本质为一定值.这又是一个数学哲学原理:量变产生质定.
最后,以定研变得不变.世间万物是相克的,其实在数学问题解决的过程中,就应用到这一数学哲学:以定研变得不变.比如,本问题中尽管PE与PF的线段长度随点P的运动而变化,经历一波三折后,最终成功突破就是依赖于△AEP∽△ADC∽△DFP和△AOP与△DOP的面积和等于△AOD的面积这些“定”的元素,就是变中不变,定的元素不仅有量定,更为关键的是数量之间的定关系,图形的形状不变与位置不变,这是问题解决的突破口,是学生解决问题所缺少的思路.也就是先从条件去联想,确定那些定元素,再来研究问题就势如破竹.若不能确定定的元素,那就意味条件没有起到作用,问题就无法解决.因而数学问题的解决必须具备以定研变得不变的“数学哲学”原理.
四、回归应用
在哲学发展的各个阶段都闪耀着数学的光芒,数学尤其是几何学对哲学的影响极为深远,通过本案例又折射出数学问题的解决离不开哲学,这就是数学哲学原理.本人通过这次反思,逐渐形成了一套解决数学问题的理念体系,把一般问题特殊化、量变产生质定、以定研变得不变统称为“数学哲学”原理.一套私下里被笔者叫做“‘数学哲学’原理”就这样诞生了.
“一般问题特殊化、量变产生质定、以定研变得不变”是经历实践反思与理论学习的综合提炼,更是在实践中不断应用而证实的产物.本人就结合具体数学问题与您一同体验数学哲学原理的魅力.
问题3:如图5,正方形的ABCD边长为1,AB上一动点E,以BE为边作正方形EFGB,则△AFC的面积为________.
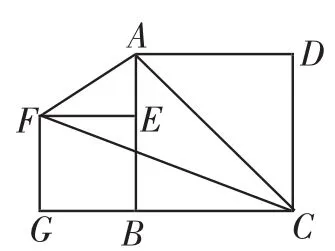
图5
本题具有一定难度,学生不能顺利解决合乎情理,原因是学生缺少数学哲学原理.试着引导用数学哲学原理去思考,学生会很快完成猜想与说理,着实让笔者更加坚信数学哲学原理的强大效应.比如,将点E特殊化,即点E与B重合时,如图6,△AFC就演变成△ABC,面积等于.当点E与A重合时,如图7,S△AFC=AF×CD×这是运用了数学哲学原理一“一般问题特殊化”去猜想结论.然后再用“量变产生质定”原理进行推理证明.如图8,设BE为x,则S△AFC=S长方形HGCD-S△FGC-S△ACD-S△AHF=1×(1+x)
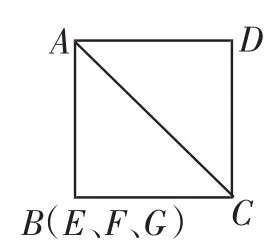
图6
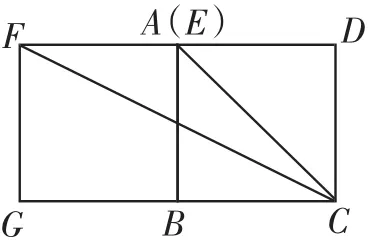
图7
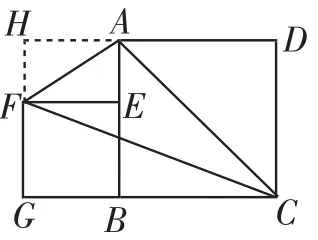
图8
通过变量表示、转化最终得到S△AFC是定值,当然在推理的过程中用到了定的本质,就是S△AFC等于长方形HGCD的面积减去S△FGC、S△ACD、S△AHF的和.由此可见“以定研变得不变”的原理是解决数学问题的核心.
问题4:已知二次函数y=mx2-2mx+3,此二次函数一定过哪两个定点,两定点的坐标为:____________.
方法一:(一般问题特殊化)令m=1,得到y=x2-2x+3;再令m=-1,得到y=-x2+2x+3,然后得到x2-2x+3=-x2+2x+ 3,解得x1=0或x2=2,y=3,即定点为(0,3)与(2,3).
方法二:(量变产生质定)既然是定点那就与变量m无关,这就要消去m,只有mx2-2mx=0,因为m≠0,所以x=0或x=2,此时y=3,即定点为(0,3)与(2,3).
方法三:(以定研变得不变)尽管m不确定,但基于条件一般式的c是定的,即抛物线与y轴的交点为(0,3),对称轴x=-=1也是定的,由抛物线的对称性得到另一定点(2,3).
问题5:如图9,已知点A(6,0),O为坐标原点,点P是线段OA上任意一点(不含顶点A,O),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图像开口均向下,它们的顶点分别为B、C,射线OB、AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和为_______.
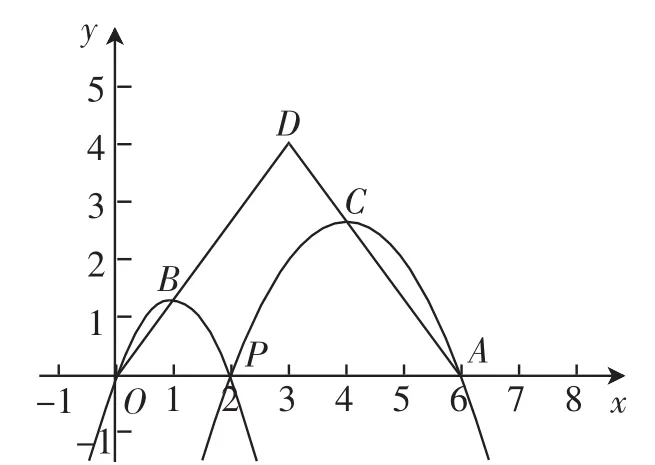
图9
方法一:(一般问题特殊化)如图10,将点P平移与点O重合,点B与点O重合,此时点C与点D重合,可知y1的最大值为0,y2的最大值为D点的纵坐标,作DH⊥x轴,垂足为H,由勾股定理可得DH=4,y1的最大值与y2的最大值之和为4.
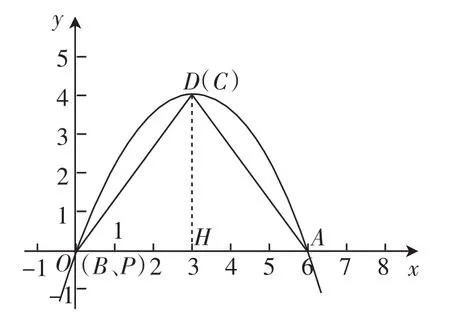
图10
方法二:(量变产生质定)如图11,在点P运动的过程中,OP的长度是变化的,为体现一般性,设OP为a,作BE⊥x轴,垂足为E,OE为;作CH⊥x轴,垂足为H,AH=,作DF⊥x轴,垂足为F.
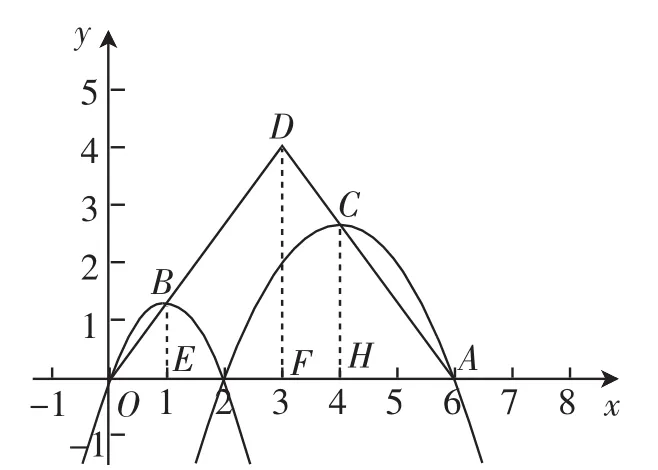
图11
方法三:(以定研变得不变)如图12,点P在滑动的过程中不变的有:△OBP、△ACP的形状不变,为等腰三角形;△OBP∽△ACP∽△ODA的关系不变;四边形BPCD为平行四边形.易证四边形CMFH为矩形,可得CH=MF;易证△BEP≌△DMC,可得BE=DM,则CH+BE=MF+DM=4.
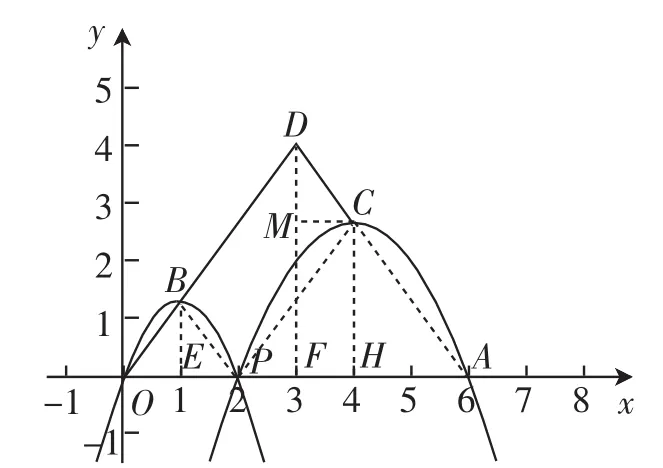
图12
这样的例子不胜枚举,其实只要时时、处处试着去用数学哲学原理思考问题,就会发现问题的本质,任何数学问题都能迎刃而解.
