把握例题精髓 彰显示范功能

☉浙江省义乌市江东中学　朱国桅



把握例题精髓彰显示范功能

☉浙江省义乌市江东中学朱国桅

例题教学是数学课堂教学的重要组成部分，是对所学知识进一步深化，同时对技巧的运用进行示范，把数学知识、解题技能和思想方法联系起来，并最终转化为能力.其质量的高低直接影响学生对数学基础知识和基本技能的掌握，同时也影响学生对基本思想的感悟和基本活动经验的积累，从而影响学生运用数学知识解决实际问题的能力.因此，把握住例题的精髓，彰显解题思路和方法上的典型性和代表性，由知识转化为能力上的示范性和启发性，应该成为初中数学教学的中心.

一、精髓——揭示本质

例1若代数式x2+2x-3可以表示为（x+1）2+m（x+1）+n的形式，则m-n的值是______.

问题1：问题中要求什么？

可以分别求出m、n，也可以直接求m-n.

问题2：如果分别求m、n，这里的m、n可以看成什么？

m、n是待定系数，可以看成未知数，关键是要得到关于m、n的二元一次方程组.

问题3：如何得到关于m、n的二元一次方程组？

把条件“代数式x2+2x-3可以表示为（x+1）2+m（x+1）+n的形式”理解为“x2+2x-3=（x+1）2+m（x+1）+n”.将（x+1）2+ m（x+1）+n展开整理得x2+（2+m）x+1+m+n，所以x2+（2+m）·x

+1+m+n=x2+2x-3，所以m-n=4.

问题4：因为x2+（2+m）x+1+m+n=x2+2x-3，所以mx= -m-n-4，x=，结果未能求出m、n的值，这是怎么回事？

事实上，条件的本质是“在x为任意实数时都有等式成立”，即是恒等式；也可看成同一个二次函数的两种不同表示形式；只有当所有对应项的系数都相等时才成立，即时才满足要求.

问题5：将恒等式x2+2x-3=（x+1）2+m（x+1）+n的右边展开，则是由繁到简的一种常用变形；如果从左到右思考呢？

事实上，将x2+2x-3配方成（x+1）2-4，条件的本质是“在x+1为任意实数时都有等式（x+1）2-4=（x+1）2+m（x+

问题6：还有其他方法得到关于m、n的二元一次方程组吗？

任意给出x两个特定的值，分别代入两个整式，就得到关于m、n的两个方程，如x =0和x =1代入得

问题7：在问题6中x能否取其他数值？

特殊性寓于一般性之中，一般情形成立的结论特殊情况下一定成立；要说明特殊情形下的结论在一般情形下成立必须经过一般性证明.作为填空题毋庸置疑，但如果作为解答题，则必须进行一般性的验证.

问题8：如何想到直接求m-n？

在代数式（x+1）2+m（x+1）+n中，给定x的具体数值就可出现关于m与n的代数式，如：当x=0时，有m+n；当x=1时，有2m+n；当x=m+n；….那么怎样才能出现m-n呢？因为m的系数为（x+1），n的系数为1，要出现m-n，m、n的系数必须是互为相反数，所以x+1=-1，即x=-2.当x=-2时，有（-2）2+2×（-2）-3=（-2+1）2+m（-2+1）+n，化简整理得-3=1-m+n，所以m-n=4.

例题是数学知识的载体，它集知识性、典型性、探索性于一体，更是学生学习数学知识的范例.就题论题，体现不出例题的导向作用和举一反三的效果.例题教学的精髓是引导学生经历探索、感悟、反思甚至尝试失败与错误的曲折过程，让学生有感而发、有感而问、有感而究，深入理解例题的本质，逐步优化思路与方法.

二、解惑——灵活应用

例2已知P（x1,y1）和Q（x2，y2）为抛物线y=-mx2+ 2mx+1（m＞0）上的两点，若x1＜1＜x2，且x1+x2＞2，请比较y1、y2的大小.

学生的困惑1：二次函数的解析式不确定，则相应的函数图像与性质能知道吗？

学生的困惑2：二次函数图像上点的位置与点的纵坐标的大小有何关系？

学生的困惑3：抛物线对称轴两侧的两个点的纵坐标如何比较大小呢？

学生的困惑4：P（x1，y1）、Q（x2，y2）两点在二次函数图像上的位置能确定吗？

学生的困惑5：抛物线上点的纵坐标即为相应的二次函数值，则能代入解析式先求函数值，再比较大小吗？

解析这道题，教师可设置下列问题做铺垫：

问题1：由y=-x2+2x+1，你能说出哪些结论？

生1：这是一个二次函数，图像是一条开口向下的抛物线.

生2：抛物线的对称轴为直线x=1.

生3：当x≤1时，y随着x的增大而增大；当x≥1时，y随着x的增大而减小.

问题2：关于y=-mx2+2mx+1（m＞0），上述性质有变化吗？

问题3：若（-1，y1）和（3，y2）为抛物线y=-mx2+2mx+1 （m＞0）上的两点，则比较大小：y1______y2.

问题4：若（-1，y1）和（2，y2）为抛物线y=-mx2+2mx+1 （m＞0）上的两点，则比较大小：y1_____y2.

生4：因为（2，y2）关于对称轴直线x=1的对称点（0，y2）也在抛物线y=-mx2+2mx+1（m＞0）上，-1＜0，所以y1＜y2.

生5：因为（-1，y1）关于对称轴直线x=1的对称点（3，y1）也在抛物线y=-mx2+2mx+1（m＞0）上，2＜3，所以y1＜y2.

生6：因为1-（-1）＞2-1，所以点（-1，y1）离对称轴直线x=1的距离比点（2，y2）离对称轴直线x=1的距离远，所以y1＜y2.

生7：当x=-1时，y1=-3m+1；当x=2时，y2=1.因为y1-y2=-3m，m＞0，所以y1-y2＜0，所以y1＜y2.

教师通过不断创设一定梯度且前后连贯的问题情境，激发学生的思维，获得启发后明晰思路，寻求突破.

解法1：设点Q关于直线x=1的对称点为Q′（x0，y0），则x0=2-x2，y2=y0.因为x1+x2＞2，所以x1＞2-x2=x0.因为x1＜1＜x2，所以x0＜x1＜1.又因为抛物线的开口向下，当x≤1时，y随着x的增大而增大，所以y0＜y1，即y1＞y2.

解法2：因为x1+x2＞2，所以x2-1＞1-x1.又因为x1＜1＜x2，所以点Q（x2，y2）到对称轴直线x=1的距离大于点P（x1，y1）到对称轴直线x=1的距离.又因为抛物线的开口向下，所以y1＞y2.

解法3：因为P（x1，y1）和Q（x2，y2）的中点的横坐标为，又因为x1+x2＞2，对称轴直线x=1，所以中点在对称轴的右侧.又因为x1＜1＜x2，所以点Q（x2，y2）到对称轴直线x=1的距离大于点P（x1，y1）到对称轴直线x=1的距离.又因为抛物线的开口向下，所以y1＞y2.

例题的解析不仅仅是要让学生知道结果，更重要的是教师要在学生感到迷茫的时候，善于层层剥茧，直指问题要害，让学生看到方向，并让他们找到解决问题的方法.好的问题设计具有较高的数学思维含量，能起到较好的引疑、激疑、释疑作用.一题多解可以从不同角度、不同方位思考问题，是提高分析问题和推理能力的一种极好的思维方法.在设计问题时，要拓展问题的思考空间、增加问题的探究属性，让学生能够多角度、多层次地展开思考，为学生的创新注入动力.

三、渗思——深思提能

例3如图1，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为（）.

A.①②B.②③C.①③D.①②③

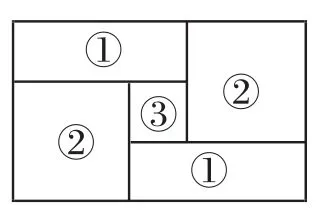
图1

分析：本题考查的内容有矩形、正方形、中心对称图形的性质，数与式、定值问题，将方程思想、整体思想、数形结合思想、转化思想和平移方法融汇在基本图形中，更多地关注学生的思维能力和创新精神、洞察力，是融PISA理念和初中数学思想于一体的典型范例.

解法1：设住房平面图长方形的长为a，宽为b，正方形②的边长为x，正方形③的边长为y，从横向考虑有大长方形的长等于2个正方形②的边长与1个正方形③的边长的和，从纵向考虑有大长方形的宽等于2个正方形②的边长与1个正方形③的边长的差，由这两个等量关系可得关于x、y方程组解得所以长方形①的周长为2［（x+y）+（x-y）］=4x=a+b，正方形②的周长为4x=a+b，正方形③的周长为4y=2（a-b）.所以当给定大长方形的周长时，标号为①②的图形周长为定值，故选A.

解法2：运用转化（平移）的思想，如图2，将线段GN平移到DP处，线段PE平移到NB处，即GN=DP，PE=NB.又因为PE=EH+PH=GH+PH，所以长方形①的周长=CP+NG+GH+PH+ CN=CP+DP+PE+CN=CD+NB+ CN=CD+CB.

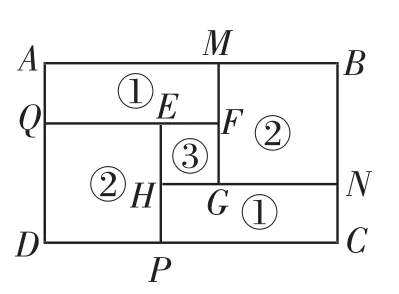
图2

将线段PH平移AQ处，线段QF平移到PC处，即PH= AQ，QF=PC.又因为QF=QE+EF=QE+EH，所以正方形②的周长=DP+QE+EH+PH+DQ=DP+PC+DA=DC+DA.所以标号为①②的图形周长均为大长方形的周长的一半，即只知道原住房平面图长方形的周长，分割后①②图形不用测量就能知道周长，故选A.

数学思想方法比数学知识更抽象，思想方法的教学是一种数学活动的过程，重在领会应用，学生的参与显得尤其重要.因此，在例题解析时先让学生有自己的切身体验，逐步领悟大长方形的任意性、满足要求的分割的存在性、唯一性及可操作性，体验特殊的数量关系与位置关系、沟通与关联的转化思想和整体思想，体验用字母表示图中有关线段的长度而体现的符号意识和数形结合思想，通过方程思想进行数式的运算是进行数学思考和表达的重要形式，用自己的思维方式构建出数学思想方法的体系，当经验和领悟积累到一定程度，数学方法就会凸现出来.

总之，例题教学是数学教学非常关键的一环，不仅关于学生数学概念、定理、性质、公式等知识的掌握和综合运用，更是对学生数学思维方式、思维品质的关键示范.因此，教师在教学准备中要认真研究、准确判断和挖掘其功能和价值、进行合理的预设，在例题解析中要充分发挥学生参与活动的主动性，给学生充分的思维活动空间，引导学生进行顺势而思自然得法，要把握例题精髓，重视常规例题解决，强化通性通法提炼，注重对解法的思辨与优化和适度的变式拓展，追求真实、有效的方法，使学生牢固掌握演绎推理的解题方法，深刻感悟数学思想，有效启迪数学研究方法，从而实现从知识向能力的转化和提升数学思维品质.

参考文献：

1.潘红玉.推进思辨活动彰显示范功能［J］.中学数学教学参考（中），2015（7）.

2.刘光才.溯本求源追求通法注重思想［J］.中学数学教学参考（中），2015（5）.

3.钱德春.对数学解题“繁”与“简”的辨析与思考［J］.中学数学杂志，2015（10）.

4.谢胜斌.掌握例题精髓创设高效课堂［J］.中国数学教育，2015（7-8）.