常规思维与个性思维，孰优孰劣——由一道期中复习题引发的思考

☉江苏省无锡市港下中学　程　军



常规思维与个性思维，孰优孰劣——由一道期中复习题引发的思考

☉江苏省无锡市港下中学程军

一、写在前面

在迎接初三第一次期中考试复习期间，碰到以下题目，其中关于第三问中OE的求法，同行教师间展开了激烈的讨论，呈现不同思路！但学生的解法八仙过海，各显神通，似乎更胜一筹，值得教师反思、总结！（事后对两个班级中解法比较典型的学生进行了访谈）

题目：如图1，平面直角坐标系中，已知A（8，0）、B（0，6），⊙M经过原点O及点A、B.

（1）求⊙M的半径及圆心M的坐标；

（2）过点B作⊙M的切线，求直线的解析式；

（3）BOA的平分线交AB于点N，交⊙M于点E，求点N的坐标和线段OE的长.

注：第一、二问解法省略，第三问中N的坐标解法也省略，其中N

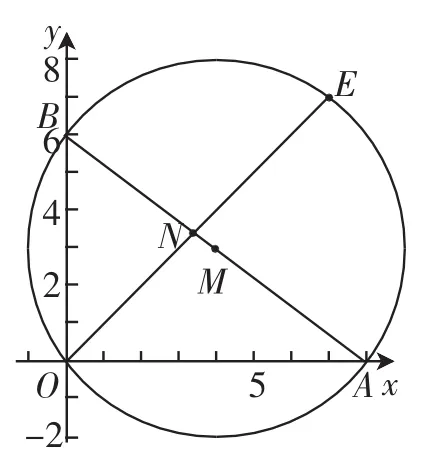
图1

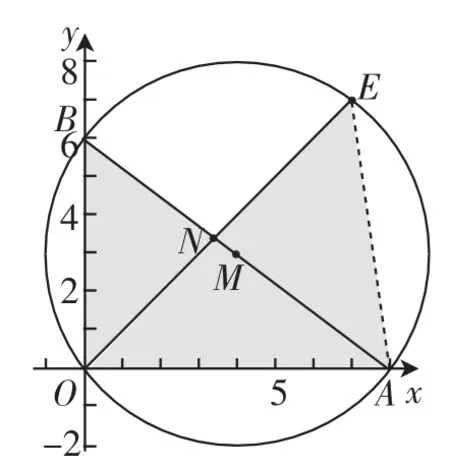
图2

二、学生解法面面观

学生A——解法1（如图2）.

思路：连接AE，直接用△BON与△EOA相似，列出比例式，

事后访谈：你是如何想到这样简洁的方法的？

学生A：求OE，用相似三角形，连接AE，看出△BON与△EOA相似！直觉告诉我，连接EA，然后就找到这两个三角形！

反思：这种解法触到问题的实质，在圆的背景下，求线段长度，一般可以考虑通过相似解决问题，这也是初中数学中求线段的常见思维方法，不过看出这样两个三角形是不简单的，主要原因是涉及四条线段，找两个三角形有点儿难，一次成功，可谓解法精简、扼要！

学生B——解法2（如图3）.

图3

思路：连接BE、AE，△ABE是等腰直角三角形，求出BE=

事后访谈：你为什么用到两次相似？一次不是更简单？

学生B：由OE是角平分线，得AE=BE，可求出AE或BE的长，圆中△BEN与△OAN定相似（且相似比为，再加上ON已知，可先求BN，NE与AN是对应边，故要求出AN，最终获得成功.但没有一次看出△BON与△EOA相似，是边走边看，先观察到△ABE，容易发现△BEN与△OAN相似，求出AN，最终列出与NE相关的比例线段，是走了点儿弯路.

反思：该学生的解法也属情理之中，想到连接BE、AE，并判断出阴影三角形相似，这两个三角形相似比学生A看出的两三角形相似要简单，思维量相对较小，通过求出NE最终求得OE的长，是属于典型的小步子，快节奏，脚踏实地，逐步成功的例子.应该讲这样的思维是常规思维，值得学习.

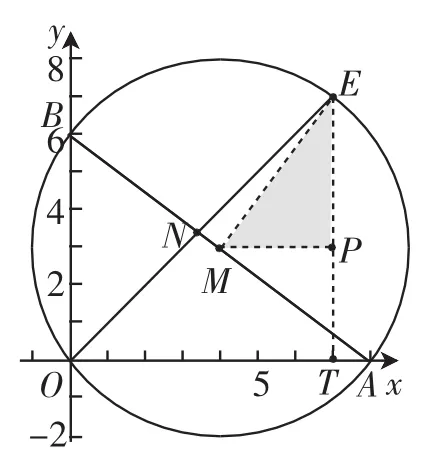
图4

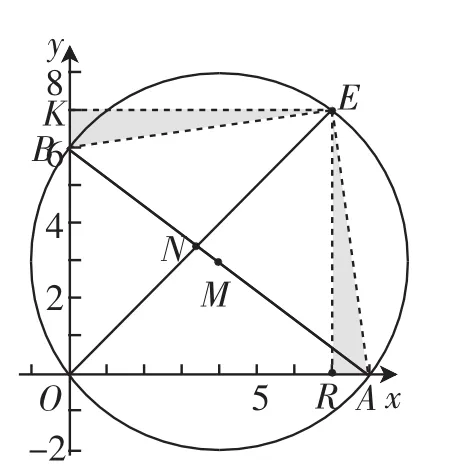
图5

学生C——解法3（如图4）.

思路：过E作ET⊥OA，过M作MP⊥ET，连接ME，设ET=a，则EP=a-3，MP=a-4，

由勾股定理得（a-3）2+（a-4）2=25，解得a=7，故OE=

事后访谈：你为什么想到作ET⊥OA和MP⊥ET？

学生C：求OE的长，联想到OE是角平分线，故作ET⊥OA，△ETO是等腰直角三角形，只要求出ET即可，由于M的坐标已知，故过M再作MP⊥ET，最后利用勾股定理.

反思：求线段OE的长，作垂线，构造直角三角形也是初中数学中常见的基本方法.利用半径、弦心距等构造直角三角形并很好地利用勾股定理解决问题，也是初中数学中求线段常见的思维方法，值得学习.

学生D——解法4（如图5）.

思路：过E作ER⊥OA，EK⊥OB，利用OE是角平分线，得四边形EKOR是正方形.

由EA=EB，得△ERA与△EKB全等，则RA=KB.设 ER=x，则8-x=x-6，解得x=7，故

事后访谈：为什么你能看出RA=KB来？

学生D：完全是直觉！OE是角平分线，结合求OE，作ER⊥OA，EK⊥OB，利用AR=BK，求出ER，这里看出AR= KB十分关键！全等三角形显神威！

反思：作垂线ER应该能想到，但再作一条EK就不太容易了，能看出AR=KB来，没有一定的灵感恐怕较难，利用全等知识（几何知识）证明之，不失为一种巧妙的方法，得到8-x=x-6这一简洁式子更是石破天惊！学生的思路是何等开阔，个性化思维精妙绝伦！

学生E——解法5（如图6）.

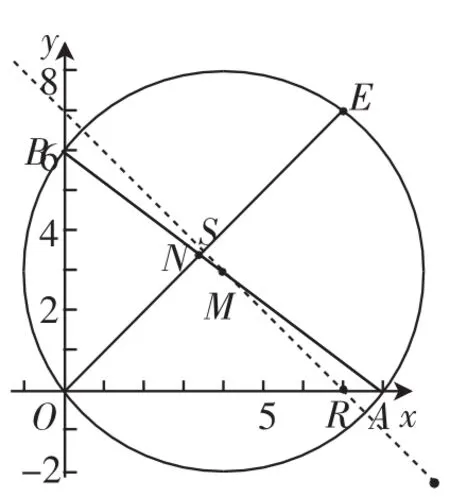
图6

思路：过M作直线MS⊥OE，直线MS与x轴的夹角为45°.由 M（4，3），得直线MS的解析式为y=-x+7.S为两直线l1：y= x、l2：y=-x+7的交点，构成方程组，求出点S为OE的中点，故E的坐标为（7，7），故OE=

事后访谈：为什么想到作这样一条漂亮的直线？

学生E：作直线MS⊥OE，根据∠EOA=45°，知道该直线与x轴的夹角为特殊角，且M（4，3），所以直线MS的解析式可求，即y=-x+7，结合直线y=x，快捷求出S点.又S为OE的中点，E点也随之求出，最终求出OE的长.解析法在这里大显身手！

反思：过圆心M作MS⊥OE，并不稀奇，可贵的是居然作出这样的直线来，竟把S看成是两直线的交点，更是不可思议，也是妙不可言！利用两直线的交点（解析法）求出坐标，进而直接写出E点的坐标，可谓剑走偏锋，匠心独具，这样的个性思维有很可贵的创造性，不拘一格，多珍贵的想法啊，小心呵护才是.

三、关于通性通法和个性解法的两点思考

常规思维往往涉及通性通法，解题方法具有普遍指导意义，是初学者学习解题的必然选择.所谓通性通法，是指具有某些规律性和普遍意义的常规解题模式和常用的数学思想方法.数学属于思考型的学科，在解题过程中理性思维起主导作用，本题解法众多，属“多解归一”，这里的“一”就是具有普遍意义和广泛迁移性的、“含金量”较高的那些策略性知识，也即从题目中“提炼”反映数学本质的东西.

1.常规方法往往能渗透数学思想，触及数学的本质，是解题本色

解法1、解法2、解法3是常规思维.初中阶段，求线段长一般做法是建立方程，而勾股定理和相似三角形（包括解直角三角形）就是构造方程的有力工具！这也是学生求线段长的基本方法，是根！它触及了数学中的方程思想.本题中求OE的常规想法是找相似三角形或构造直角三角形，找相似三角形往往比较难，涉及4条线段、两个三角形，图形较复杂.但一旦找到，解决问题很简洁！解法1和2都属于这一类，但显然解法2是小步子快节奏，没有解法1简洁.解法3就是比较典型的构造勾股定理的方法，属常规思维.这三种解法是基本思路，是初中阶段学生求线段长的基本方法，具有普遍规律，即使到高中，求线段长一般也是归到三角形相似或直角三角形来研究，主要是采用方程列等式.这是初学者解题的必然选择，上述三种方法归“一”，这个“一”就是要建立方程，找到相似（列出比例式）或构造直角三角形相似（根据勾股定理列方程）建立等式.

2.个性方法往往独具匠心，植根于常规思维，但又高于常规思维，是解题花色

个性解法往往给人意想不到的精彩，想法独特，富有魅力.但个性思维也来源于常规思维，解法4中作垂线ER、EK就是常用手法，但能看出AR=KB，就是一种独到想法，是一种灵感，往往说不出为什么，但仔细观察，发现该做法充分利用OE是角平分线这一条件（ER=EK，EB=EA），想到全等三角形，得出RA=KB这个结论，却石破天惊，学生利用它建立一元一次方程，轻松求出ER，再利用直角三角形ERO，快速求出OE的长.

可见，这种富有魅力的解法也有先决条件，那就是对角平分线的性质要了熟于心，并用足条件，可以看出，得到全等三角形是最大亮点！从而突破了常规思维——分步求线段长，避开了烦琐的计算，一步到位，实现了解题的最优化.

对于解法5，有常规思维的痕迹，例如求直线的解析式（已知直线的倾斜角和已知点）和求直线交点的坐标（两直线的解析式联立构成方程组求交点的坐标），但更有突破常规之处，那就是：求线段长，通过求点的坐标来实现！本解法的魅力所在就是构造直线MS和通过点的坐标求线段的长度，值得回味，但这种做法不具有普遍性！若OE不是角平分线，解析法就未必简单，若没有S是OE的中点这一条件，求OE的长就复杂了！故要看清这种解法的特殊性和局限性.

四、写在后面

常规思维和个性思维各有特色.对于多数学生，应掌握普遍的解题规律，这是解题的根，也是一般都适用的基本方法.常规思维也是解题者适应解题的必然选择，是解题的必然王国.个性思维不是空中楼阁，它是解题者在常规思维基础上的突破，是解题普遍规律和自身特色的结合和升华，是解题的自由王国！常规思维，解题应该有法；个性思维，解题也能“解无定法”！