老“歌”新唱，唱的响亮——一节一次函数单元复习课的教学设计与反思

☉江苏省睢宁县教育局教研室　戴文革☉江苏省睢宁高级中学附属初中　汤　庆



老“歌”新唱，唱的响亮——一节一次函数单元复习课的教学设计与反思

☉江苏省睢宁县教育局教研室戴文革
☉江苏省睢宁高级中学附属初中汤庆

2015年12月28日，睢宁县在一农村中学举行了一次初中数学“走乡村—真教研、真学习”教学研讨活动.此次活动以期末复习课教学为研讨主题，活动前一周提前告知课题，各学校备课组集体备课，活动当日现场抽签，随机确定教师课堂展示.活动充满了较浓厚的“真教研、真学习”教研氛围，特别是活动中的一节“一次函数的复习”课引起了较强烈的反响.如何有效地梳理、应用、复习巩固一次函数的概念、图像和性质，使学生在新课学习的基础上对一次函数有一个更完整、更深刻的认识，让复习课这首老“歌”被唱出新意、唱的响亮？执教者在教学设计过程中以系列问题串为主线，以渗透数学思想方法为主旨，以学生自主探究为核心，以小组合作学习为辅助，取得了较好的教学效果，对这一问题给予了较好的诠释，也获得了一致好评.以下是此设计与反思，敬请大家思考与批判.

一、教学设计

（一）情境引入——品味经典

教师出示两个经典故事数学问题.

情境1：乌鸦喝水问题.

如果设衔入瓶中石子的体积为x，瓶中水面的高度为y，下面能大致表示上面故事情节的图像是（）.

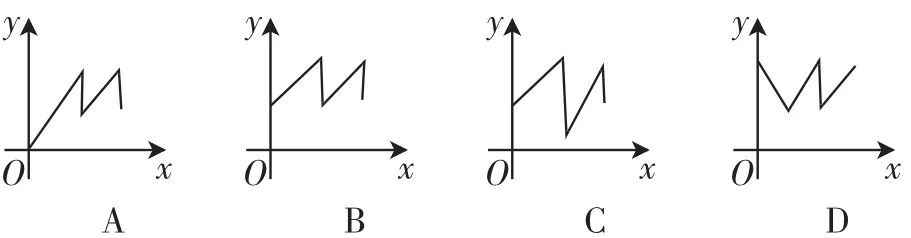
情境2：龟兔赛跑问题.

有一天，龟、兔进行了600m赛跑.如图1表示龟兔赛跑的路程S（m）与时间t（min）的关系，根据图像回答以下问题.

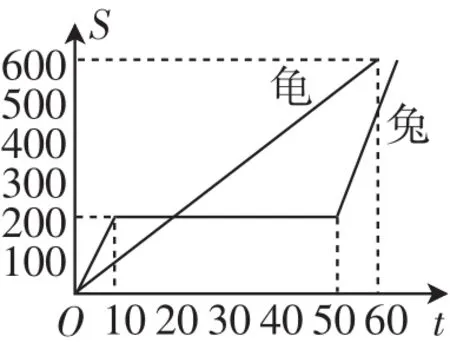
图1

（1）赛跑中，兔子共睡了多长时间？

（2）写出乌龟跑的路程S（m）与时间t（min）的函数关系式.

（3）赛跑开始后，乌龟在第几分钟时从睡觉的兔子旁经过？

设计说明：教师先出示问题1，学生独立思考并回答问题，再出示问题2，学生独立思考（1）、（2）两个问题，并展示答案.同桌合作完成（3），并汇报合作结果.由此引出课题：看“图”识“函数”——一次函数图像信息类问题（教师板书）.

设计意图：教师通过两个经典问题——乌鸦喝水、龟兔赛跑情境引入，意图是：（1）品味经典故事，引起学生对本节课的学习兴趣；（2）通过经典故事，引发学生对实际问题的思考，特别是对函数图像的认识.

（二）建构活动

活动1：自主先学.问题情境（同时同地1）.两位参会教师同时从县城出发前来参加活动，教师甲、教师乙分别乘汽车、骑摩托车.如图2所示表示他们行驶的路程s（km）与行驶时间t（min）之间的关系.根据图像回答以下问题.

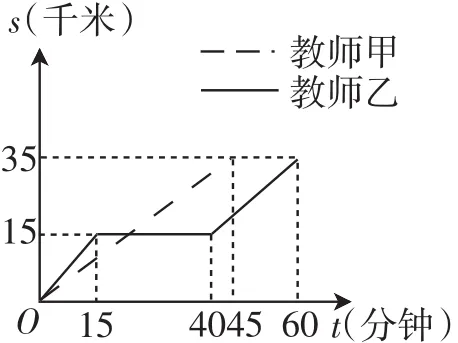
图2

（1）横轴表示：______，纵轴表示：______.

（2）县城到活动地点的路程：______km，老师甲共用______分钟，老师乙共用______分钟.

（3）老师乙中途休息______分钟，老师甲比老师乙早到______分钟.

（4）写出老师乙在休息后行驶的路程s（km）与时间t （min）之间的函数表达式，并指出自变量的取值范围.

设计说明：教师先出示问题，同学们根据提出的问题，独立思考并回答问题.教师根据学生的回答情况给予指导.学生根据教师提出的问题情境，独立看“图像”，通过“图像”理解题意，解决问题，同桌两位同学比较自己所得答案，然后形成共同答案，最后汇报成果.

设计意图：以教师参加教研活动的行程为“主线”作为问题情境，引发学生对本节课内容的探索，以教师甲与教师乙同时同地出发前往活动地点为问题设计“出发点”，用身边的“真”情境，可以激发学生的探究欲望，激活学生的火热思考.

活动2：合作助学.

问题情境（同时异地1）.

如果教师甲从县城出发前往参加活动，教师丙从庆安水库同时出发前往参加活动，在行驶过程中，他们的行驶速度不变.如图3所示是他们与县城之间的距离S（km）与行驶时间t（min）之间的关系.根据图像回答问题.

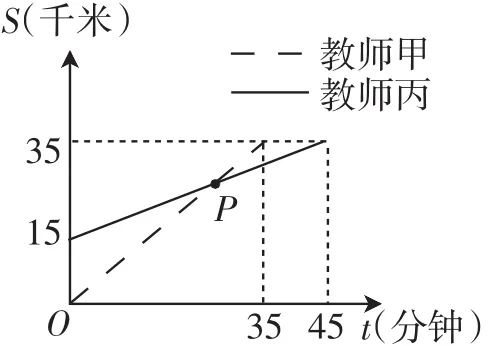
图3

（1）庆安水库距县城________km.

（2）写出教师丙与县城之间的距离S（km）与行驶时间t（min）之间的函数表达式，并指出自变量t的取值范围.

（3）图像中点P表示的实际意义是______________.求出点P的坐标.

（4）如果教师丙想从庆安水库去县城办事，按上面的速度，他需要多长时间到达县城？

知识总结归纳.

解答图像信息题主要运用数形结合思想，化图像信息为数字信息.

（1）______________________________________.

（2）______________________________________.

（3）______________________________________.

设计说明：教师出示问题，学生根据问题独立思考问题，然后小组内合作讨论，并形成决议.教师在小组合作过程中，参与其中，与学生互动.学生先独立思考（1）、（2）两个基本问题，然后以（3）、（4）两个问题作为小组合作交流讨论的“中心”问题.学生形成共同答案后，其中一组的组长汇报，而后其他组长补充.学生根据老师提示尝试归纳：（1）了解横、纵轴的意义；（2）从图像形状上判定函数与自变量的关系；（3）抓住特殊点的实际意义.

设计意图：活动2合作助学的设计，意图在：其一，以“参加活动”为问题载体继续引起学生对本节课的探索；其二，通过小组合作助学选择核心问题（2）、（3）两问获得本节课的知识要点，进一步领会对一次函数图像本质的认识.

活动3：交流展示.

问题情境（同时同地2）.

教师甲、教师丁同时分别从县城去距离35km的姚集中学参加教研活动，两人在整个过程均保持匀速运动，教师丁在抵达活动地点后有事随机返回（速度不变）.设他们行驶时间为x（min），他们两人的距离为y（km）.他们从出发到途中相遇y与x之间的函数关系如图4所示.根据图像提供的信息，解决下列问题.

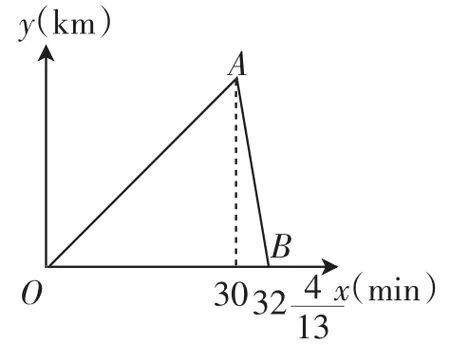
图4

（1）图中点A的实际意义为_______________.

（2）求教师甲、教师丁的速度.

（3）求线段AB所表示的y与x之间的函数表达式.

（4）从出发到相遇，当x为何值时，教师甲、教师丁相距1km？

设计说明：教师出示问题后，将本题作为“主例题”讲解，并板书规范的解题过程.教师要求学生先独立思考，然后小组合作（教师引导相结合）.学生根据教师要求先独立思考图像中的横、纵轴表示的实际意义是什么，然后小组合作（教师参与其中），在合作过程中，一生到黑板前板演.

设计意图：本问题情境的设计取材于行程问题（同时同地折返），函数图像上的横、纵轴表示的实际意义与前面的问题情境截然不同，目的是通过前面问题的适当变式，让学生能通过“看图”真正“识图”，即“慧眼识珠”.

活动4：质疑拓展.

问题情境（同时异地2）.

想一想：你能用本节课的知识给图5添加合理的情境吗？

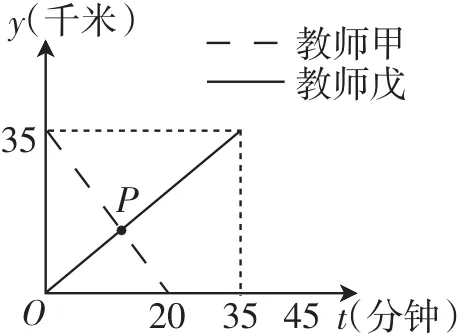
图5

设计说明：教师出示问题，引导学生充分思考，添加不同的问题情境，小组合作，交流讨论，让不同思想火花出现.学生根据教师给出的函数图像，充分思考，小组讨论，探索交流，不同的小组会出现不同的问题情境，教师参与小组活动.

设计意图：本活动设计意图是：其一，不给学生具体问题作载体，让学生思想不受教师束缚，充分激发学生的思想火花；其二，通过本活动让学生在小组活动中“真活动”“真探索”，体会数学的真谛.

活动5：小结思考.

问题：同学们，你们能通过本节课的探索，以两位老师参加完本次活动回各自学校为问题载体，先画出函数图像，再根据图像提出问题吗？

设计说明：教师出示问题，学生根据老师的要求思考、设计.（学生可以合作、交流讨论）.

设计意图：用“问题”作为小结的载体，以开放、灵活的方式搭建起学生与学生、教师与学生之间的和谐关系.特别是在一节复习课的结尾，通过一堂课的再学习、再探究、再思悟，学生的认识肯定会有一个质的飞跃，能说的内容也就更多，教师此时要给学生一个充分展示自我的平台，把“说”的机会充分还给学生.

二、教学反思

问题是数学的心脏.章建跃老师提出教学设计的两个关键之一就是“提好的问题”.“好问题”有两个标准，即有意义，并且在学生的最近发展区内.“有意义”就是指所提问题要反映当前学习内容的本质，“在学生的最近发展区内”的问题才能形成认知冲突、激发求知欲、激活思维，才能使学生的心理保持积极的适度的求知倾向.作为一节复习课，用两个经典的故事情境引入，用学生身边的真实生活实例为背景设计系列问题串，整堂课的“行程类”问题依次呈现、环环相扣、浑然一体，不仅激发了兴趣，而且激活了思维，基本贴合了章老师的“好问题”的两个标准.

数学思想方法是数学大厦的基石.日本著名的教育家米山国藏指出：“作为知识的数学出校门不到两年可能就忘了，唯有深深铭记在头脑中的数学精神、数学思想、研究方法等，这些随时随地发生作用，使人们终身受益.”数学复习课贵在对学生进行数学思想方法的渗透.本课例中的系列问题的解决过程不乏数形结合思想、模型思想、分类思想等思想方法的渗透，学生每探究完一个具体的问题之后，教师都请学生归纳解决问题的一般方法，及时和学生分享所运用到的数学思想，充分体现了教师对“四基”中基本思想方法教学及基本活动经验的理解，注重对学生进行“四基”的训练，有效地提升了学生的数学素养.

课程标准指出：“学生学习应当是一个生动活泼、主动的和富有个性的过程.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.学生是学习的主体.”在本课例的教学过程中，更多的是学生生动活泼的独立思考、自主探索和个性展示，学生能自己独立解决的、能表达的、能展示的内容，教师给学生平台，把更多的机会放手给学生，让问题由学生自己用脑去思考，让规律由学生自己用眼去发现，让运算由学生自己用手去操作，让观点由学生自己用口去表达.事实上，这节复习课，由于知识点都是学生已知的内容，学生自主探究的空间更广，更利于体现“有效的教学活动是学生学和教师教的统一，学生是学习活动的主体，教师是学习的组织者、引导者和合作者”的基本理念.

新课程强调：认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式.合作学习作为一种重要的学习方式和教学组织形式，不单单体现在新授课上，复习课上也应充分体现.不是随便的一个问题就能让学生去合作，有效的“合作学习”既要有合适的问题素材、恰当的呈现时机，又要有教师适时的引导.本课例中，执教者安排了多处小组合作讨论的环节，应该说在选取问题的难度、小组讨论的时机、引导分寸的把握等方面都处理的较为妥当，正所谓教之道在于“度”.例如，本节课的课堂小结就是以一个开放式的问题为载体，让学生自己去编题（画图像并提出问题，再解决问题）.这样的小结方式给学生更大的思维空间，使复习课的立意在课尾进一步升华，通过“小组合作”交流碰撞，让不同层次的学生通过一节课的学习都能对一次函数的学习有一个新的认识，碰擦出更耀眼、更精彩的思维火花.

复习课是一种常见课型，其教学最主要的任务就是“温故而知新”.复习课的教学设计应以学生所求、学生所需为出发点和落脚点，只有这样，才能使学生积极参与复习教学的全过程，真正发挥他们的主体作用.本课例虽然有一些创新的设计元素，实际的教学效果也较为理想，但仍然存在不少问题和困惑，比如，怎样使“生活实际问题数学化”更科学、更规范、更严谨？如何更合理地安排一节课的教学容量，从而切实实现复习效果的最大化？敬请各位同行批评指正、不吝赐教.

参考文献：

1.曹才翰，章建跃.中学数学教学概论［M］.北京：北京师范大学出版社，2008.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

3.王利庆.渗透分类、方程思想，凸显复习主题［J］.中学数学教学参考（中），2013（6）.

4.戴文革.“合作学习”不能盲目走“偏”［J］.中小学数学（初中），2015（5）.