用是最好的学

摘 要 用是最好的学，有效的课堂教学应该始终围绕学以致用、以用促学、学用互哺的思路进行设计。

关键词 数学教学 学习金字塔理论 以用促学 学用互哺

《义务教育数学课程标准》明确提出：“为了适应时代发展对人才培养的需要，数学课程还要特别注重发展学生的应用意识。”应用意识有两个方面的含义，一方面，有意识地利用数学的概念、原理和方法解释现实世界中的现象，解决现实世界中的问题；另一方面，认识到现实生活中蕴涵着大量与图形有关的问题，这些问题可以抽象成数学问题，用数学的方法予以解决。

学习金字塔理论是美国缅因州的国家训练实验室的研究成果，它用数字形式形象地显示了：采用不同的学习方式，学习者在两周以后还能记住的内容的多少（平均学习保持率）。在塔尖，第一种学习方式——“听讲”，也就是老师在上面说，学生在下面听，这种我们最熟悉、最常用的方式，学习效果却是最低的，两周以后学习的内容只能留下5%；第二种，通过“阅读”方式学到的内容，可以保留10%；第三种，用“声音、图片”的方式学习，可以达到20%；第四种是“示范”，采用这种学习方式，可以记住30%；第五种是“小组讨论”，可以记住50%的内容；第六种是“做中学”或“实际演练”，可以达到75%；最后一种在金字塔基座位置的学习方式，是“教别人”或者“马上应用”，可以记住90%的学习内容。因此，在初中数学教学过程中，教师应该有意识地培养学生的应用意识，引导学生学后即用、以用促学、学用互哺，这样，我们的课堂才是有趣的、充实的，更是高效的。

不久前，笔者参加了李庾南实验学校专家讲师团成员的课堂教学考核活动，在南通市启秀中学开设了一堂人教版九年级“圆”第1课时的公开课。因为这是一章的起始课，概念较多，如果由老师一一讲解，就显得枯燥无味。为了能有效激发学生的学习兴趣，提升学生学习知识、应用知识的能力，根据学习金字塔理论，笔者确定了“以用促学、学用互哺”的教学思路。现将课堂教学的片段分享如下，供大家参考。

一、以用促学，激发学生的求知欲

课堂上引入源于生活的情境，能很快吸引学生的学习注意力。

师：圆是生活中常用的几何图形，圆形物体在生活中随处可见。圆具有独特的对称性，因此常被用来设计成精美的图案。比如下图中4所百年名校的校徽，都被设计成圆形图案。

设计意图：这组圆形图案的展示，既让学生感受到作为启秀学子的自豪感，又激发了学生积极向上、奋发有为的使命感，更让学生对学好圆的相关知识产生了强烈的渴望。

再如，在对弦、弧等概念教学时，笔者也进行了精心的设计，从生活中的圆形物体出发，抽象成几何图形后，抛出问题让学生通过自学找到问题的答案，并向全班进行展示。

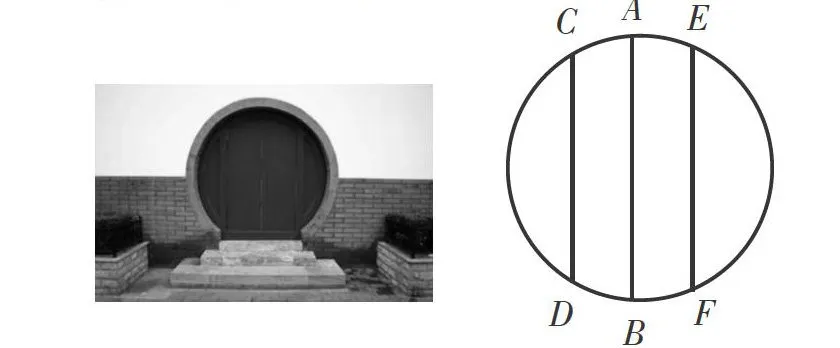
师：如图，这是一扇古建筑中的圆形木门，我们将它抽象成几何图形。

师：我们看到，图中除了有熟悉的圆心、直径外，还有一些线段，以及一些被圆上的点分割的部分，这些都是与圆有关的量，请阅读课本，了解它们的含义。

学生认真阅读，用笔圈画关键词。

师：哪位同学愿意上来与大家分享一下你的自学成果？

学生结合图形展示与圆有关的量：弦（直径）、弧（半圆、优弧、劣弧）、等圆、等弧。

设计意图：将现实生活中的实际问题抽象成数学问题，抛出问题，促进学生学习，可以有效地提高学生的学习积极性。学生感受到的是数学源于生活的真实，是可以学以致用的。这是自主学习向被动学习的挑战，因为学生强烈的应用意识驱使他们要用心学好这些知识。

二、学用互哺，提升学生的学习力

在对圆的定义的理解过程中，一些学生只能体验到外在的、浅层次的知识，课上能听懂，但课后遇到问题时又不能解决。因此，在通过学生动手画圆归纳出圆的定义后，笔者精心设计具有针对性的例题，及时巩固所学知识，让学生既感受到“学是为了用”，更掌握了“学是为了怎样地用”，从而深层次地理解了“用是最好的学”的道理。

师：由圆的定义我们了解到，圆上各点到圆心的距离都等于半径，我们来应用这条性质解决问题。

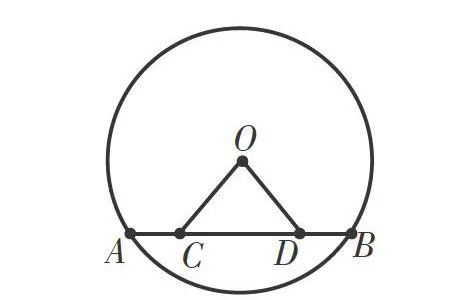
例题：如图，在圆O上有两点A、B，连接AB，若AC=BD，试判断OC与OD的大小关系。

学生展示思路1：连接OA，OB，构造全等三角形。

师点拨归纳：这种辅助线应用了圆的性质，今后要形成“作半径”的辅助线的意识。

学生展示思路2：连接OA，OB，作OE⊥AB，利用等腰三角形的三线合一、线段的垂直平分线的判定证明。

师：和刚才圆的定义一样，从它的形成过程下定义就是：经过线段的中点并且垂直于线段的直线。还记得线段的垂直平分线还有一个集合定义吗？

生回忆，师提炼：线段的垂直平分线是和线段两个端点距离相等的所有点的集合。

师：类似地，大家能归纳出圆的集合的定义吗？

生：圆可以看成到定点的距离等于定长的所有点的集合。

设计意图：根据学生的归纳，得出在一个平面内，线段绕它固定的一个端点旋转一周，另一个端点形成的图形叫做圆。学生也能理解这个定义，但不知如何应用，这就是教师经常烦恼的“学生上课也听懂了，但到课后练习时却不会做”。“学后即用”显然能有效帮助学生解决这个困惑。因此设计这条例题可以为学生指明圆的性质的应用方向。同时，学生在解决该题时，展现了思维的开放性，应用了三角形全等、等腰三角形三线合一、线段的垂直平分线的判定等知识，强化了已学几何知识在圆中的应用。由线段的垂直平分线巧妙过渡到回顾垂直平分线的集合定义，引导学生通过类比归纳出圆的集合定义，学生学起来显得很轻松，游刃有余。

师：根据圆的集合定义，可以用来判定一些点在不在同一个圆上。

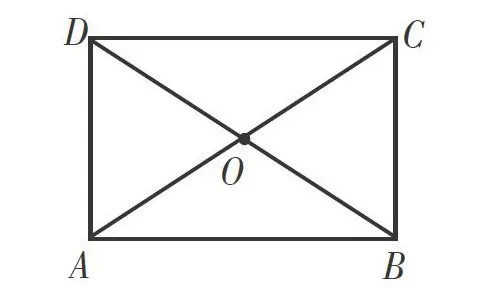
例题：如图，矩形ABCD的对角线AC、BD交于点O，求证：A，B，C，D四个点在以点O为圆心的同一个圆上。

学生独立完成后，小组交流，小组代表展示解题思路。

教师点拨：（1）找定点；（2）证d=r。

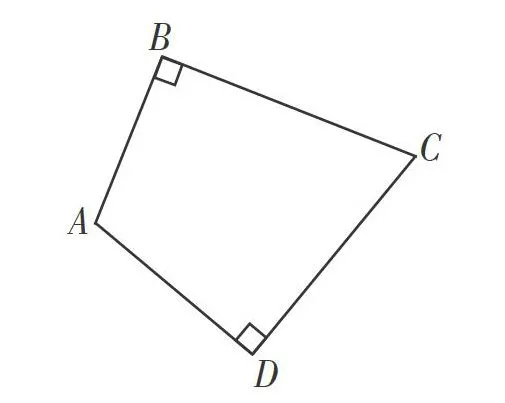
变式：如图，在四边形ABCD中，∠ABC=∠ADC=90°求证：A，B，C，D四个点在同一个圆上。

学生展示思路：连接AC，取AC的中点O，连接OB，OD，借助于直角三角形斜边上的中线等于斜边的一半可证得命题成立。

设计意图：圆还可以看成是到定点的距离等于定长的所有点的集合，根据圆的集合定义能解决哪些问题？这时候设计有针对性的“四点共圆”题组，抓住到定点的距离等于定长是判定共圆的关键，真正做到了教学过程中的“学用互哺”，这样的应用设计有效地避免了学生学习的盲目性，切实提高了课堂学习效率。

教师的选题一定要能起到“以用促学”的作用，而不能随便找些题目来充数，否则，学生还是会处于相对被动的接受状态，学习效果也不会很好。在学生证明得到了特殊四边形的四个顶点都在同一个圆上的结论后，还要进一步培养学生从特殊到一般的应用探索意识。

师：四个角是直角的四边形各顶点都在同一个圆上，一对对角是直角的四边形各顶点也在同一个圆上，那么符合什么条件的四边形的各顶点在同一个圆上呢？

生交流后回答：对角互补的四边形的四个顶点在同一个圆上。

师：这个命题作为探究性作业，请同学们在课后认真思考，遇到困难可以自学课本后几节的相关知识，以小组为单位合作探究完成。

设计意图：学习金字塔理论表明，学习效果在30%以下的几种传统方式，都是个人学习或被动学习；而学习效果在50%以上的，都是团队学习、主动学习和参与式学习。笔者设计的探究性作业，能有效激发学生主动学习、团队学习的意识，以用促学，当学生在自主解决问题遇到困难时，会自发地、主动地去获取解决问题所需要的知识点，从而有效地发展学生自主思考、合作探究的能力，提升学力。

学懂学透是基础，如果你对所学知识略知皮毛，所知不深，就难以运用；善用会用是导向，在日常生活中，特别是遇到难题时，要尝试把已学的知识用进去。教师在教学过程中，在指导学生运用数学语言表述和解决問题的过程中，要有意识地强化学生的应用意识，提升学生的学习能力。（作者为江苏省如皋市如皋初中教师）