中国沪深股市波动的实证分析

[摘要]近些年来，股票市场的波动在国际金融实证领域越发得到重视，它的各种重要特征如集聚性、非对称性和持续性等都得到许多学者的关注和研究，因此对国内股市的波动进行分析是具有重大的现实意义的。首先，对股市收益率进行描述性统计并进行诊断性分析；其次，在GRACH族模型实证探究中，经过一系列适用性检验之后，对沪深股指建立三个模型并求解；最后，得出我国沪深股指总体收益率序列波动存在显著的“非对称性效应”等一系列结论。

[关键词]收益率；集聚性；非对称性；GRACH

[DOI]1013939/jcnkizgsc201614087

1引言

人们一直都在探究金融市场上金融产品的价格变化特征和趋势，曼德勃罗和法玛研究发现了金融产品价格变化具有“波动聚类”的特性。[1]股票市场的波动性不仅随着时间而变化，而且波动具有长记忆性和持续性——如果当期市场波动幅度较大，那么紧随之后的也往往是大波动；反之，如果当期市场波动幅度较小，则下一期的波动一般也会比较小。[2]为了分析这些波动特性，很多模型被开发并改进。Engle[3]给出了ARCH模型来描述股市波动的聚类性与持续性；在此基础上，Bollerslev[4]提出了改进的ARCH模型——GARCH模型来刻画波动随时间变化所产生的异方差性；之后，Nelson引进了EGARCH模型来反映信息波动非对称波动非对称性效应，是指股票市场价格波动率对外界利好消息和利空消息的冲击表现出不同程度的

反应。的影响；Crouhy和Rockinger运用ATARCH和HGARCH模型比较分析了全球21个主要股票市场的波动特征。[5]

近些年来，对于国内股票市场的研究持续不断。在应用GRACH模型时，主要集中于运用单变量的GRACH模型对沪深股市的收益率进行拟合，以此检验股市波动性的特征。王承炜和吴冲锋研究发现，沪深股市A、B股之间是即时正相关的。另外，还利用EGRACH模型对市场波动的不对称性和“杠杆效应”进行检验。胡永宏、陆忠华等人运用这一模型进行了实证分析，结果表明，沪深股市的日收益率存在着明显的杠杆效应，收益率对波动强度的影响具有非对称性。[6]

与国外成熟股票市场相比，我国沪深股市表现出更高的复杂性和不可预测性。因此，对我国沪深股市波动非对称性进行研究具有重要的理论意义与现实意义。文章旨在运用GRACH族模型来对中国沪深股市的波动性进行刻画研究，通过比较不同模型之间的差异，得到能够较好地描述中国股票市场波动性的工具。

2数据基本特征及诊断性信息

21数据的基本统计资料

根据张剑等（2002）研究发现，1996年年底实行的涨跌停板制度对我国股市的波动产生了很大的影响，因此本文主要研究的是1997年之后我国股市波动性的特征，选取了1999年1月2日至2010年5月21日上证综合指数和深圳成分股的收盘价，共2904个观测值。

假设pt为t期的收盘指数，在探究金融产品价格变化时通常使用对数收益率来衡量：

rt=lnpt-lnpt-1

pt-1为上一期的股票指数，从而计算得到2904个沪深股市的收益率序列rsht和rszt。

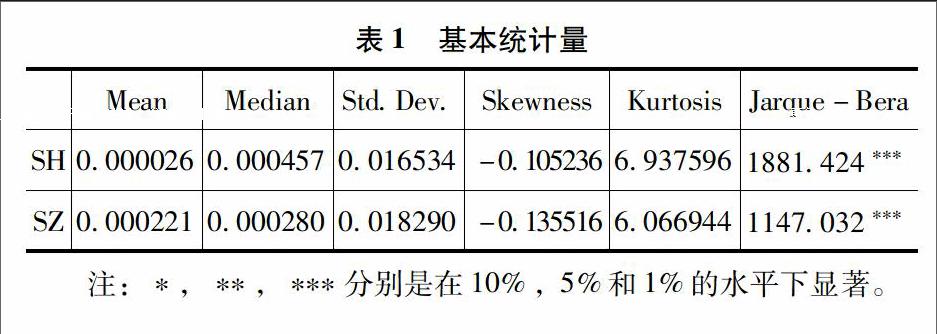
从表中可以看出，沪深两个市场的峰度达60以上，并且都带有一定的负偏态，但相比而言，沪市比深市的股指收益率分布的峰度更高，偏度更小。另外，两市收益率曲线都呈现较为明显的尖峰厚尾特征。沪市平均收益率要低于深市，但两市的最大最小值很相近，在波动性上沪市波动性略小。而从J-B统计量上可以得出，两市收益率序列都不服从正态分布。

22数据平稳性和自相关检验

对收益率序列进行平稳性检验，考虑到异方差性的影响，相比用ADF方法检验平稳性，选用 PP 检验的效果更好。PP检验结果显示沪深两市收益率序列都是平稳的，可进行预测。同时，由滞后 35 期的自相关图与偏自相关图可知上证收益率5阶以上都有较强的自相关性，且Q检验统计量很大，因此上证综合指数收益率并不是白噪声序列。而深圳成分指数收益率从3阶开始表现出较强的相关性，并一直持续到35期自相关。综上所述，沪深两市股票收益率序列都不是白噪声，缺失平稳的时间序列，可以做相关的预测。

3实证研究

31对收益率序列建立均值方程

由于沪市收益率与深市收益率的相关系数为0938，因此沪深股市的收益率之间的相关性很强，另外，从收益率曲线图中也可以直观地看出沪深收益率具有相同的走势。

在建立上市收益率的均值方程时，应该加入深市收益率作为解释变量。同样地，在对深市收益率做回归时也要将上证指数收益率作为解释变量。

rsht=0848rszt-0008rsht-1

rszt=1038rsht-0024rszt-1

从两市的收益率方程可以看出，上证指数收益率与深圳成分指数收益率的当期值表现出较强的正相关关系，其回归系数为0848，但与其自身滞后一期的系数不显著；而深圳成分指数与其滞后一期的系数显著，有一定负自相关，同时，当期沪市对深市收益率的影响作用的回归系数为1038。可以看出，相比较而言，沪市对深市的影响要更为显著一些。综上可以得出，股市当前的股价信息对后来的股价走势的影响是很显著的。

残差的PP检验显示，当最大滞后期为27时，两市的残差t统计量的p值远远小于1%，说明残差序列是平稳的，同时也表明对收益率进行拟合的均值方程是恰当的。再者，采用ARCH-LM检验对沪深市场收益率回归方程残差序列进行检验，当回归滞后期为10时，LM统计量和F统计量值都很大，p值远远小于1%，因此在显著性水平为1%下拒绝原假设，即认为残差具有异方差性。而对于异方差性的处理，本文进一步使用GARCH模型来进行拟合，以此使得方程参数的估计精度提高，从而令预测更加准确。

32GRACH模型的建立

在由上可知收益率序列存在ARCH效应的前提下，文章利用GRACH模型来对残差的波动性进行拟合。由于收益率的残差并不服从正态分布，因此在对参数进行似然估计时，需要采用一定的厚尾分布。

通过多次拟合得出多个方程，再根据AIC和SC等信息判断准则对模型进行筛选，最终选择一个最优的拟合模型。

上证综指收益率的拟合模型为：

[JZ]rsht=084rszt-0004rsht-1

[JZ]ht=008μ2t-1+0915ht-1

R2=0880DW=1807AIC=-7760SC=-7750

从上述模型可以看出，模型除常数项以外的各项系数之和小于1，表明残差的平方项是趋于平稳的。而在深市的条件方差模型中，出现了系数项为负的情况，说明模型的拟合不当，因此在文章中不予展现，从另一个方面也可以看出GARCH模型的缺陷。GARCH模型要求参数必须非负，然而在现实情况中这种非负约束往往是不能满足的。[7]

33关于中国股市非对称性的研究

为了研究上证综指与深证成指对利好与利空消息的不同反应，文章选用EGRACH这一非对称模型。EGRACH相比 GARCH模型有几个优点：第一，指数函数去除了ARCH和 GARCH模型所要求的估计系数必须为正的限制；第二，GRACH 模型对于许多金融时间序列中经常存在的明显负向不对称是非容忍的，因为该模型的条件方差由随机误差项的数值大小而非符号方向所决定，而 EGRACH模型则很好地解决了这一问题，EGRACH将标准化后的残差作为方程中的移动平均回归因子，同时还保留了数量效应的估计。

上证综合指数收益率的 EGARCH（1，1）模型：

rsht=084rszt-0006rsht-1

t=（18891）（-103）

lnht=-021+016μt-1/h05t-1-002μt-1/h05t-1+099lnht-1

t=（-891）（1562）（-313）（40231）

R2=088DW=180AIC=-776SC=-775

由EGARCH 模型可以看出，利好消息出现时，对上证指数波动率的影响系数为014，利空消息对波动率的影响系数为-018；同理可以求出，利好消息出现时，对深证指数波动率的影响系数为017，利空消息对波动率的影响系数为-015。

在面对利好消息和利空消息时，上证指数收益率和深证成分指数收益率反应程度有所差距，在对利好消息的反应上，深证成分指数比上证综合指数强；而在对利空消息的反应上，深证指数的反应程度稍弱一些。

4结论

基于GARCH类模型对国内股票市场的实证分析可以得到以下结论：

（1）通过建立均值方程，可以看出，股市中当天的信息对未来的价格走势有着显著的影响；此外，沪深两市的收益率序列的残差存在异方差性，两者都随时间而变化，明显表现出收益率波动存在一定的集聚性。

（2）运用GARCH 模型分析上证收益率的波动性，各项系数之和即衰减系数为α+β=0996， 这一系数表示信息衰减的速度很慢，当期信息对未来走势的影响作用具有持续性的特点。并且，滞后一期的条件方差对当期条件方差的影响系数为 0916，影响作用很大。相比之下，滞后一期波动的残差平方项对当期条件方差的影响作用较小。

（3）利用EGARCH模型对上证指数和深圳成指进行探究，发现上证指数收益率和深证成分指数收益率对待不同信息时具有相同趋势的反应，但程度有所差别。由此得出，沪深市场都存在显著的“非对称效应”，但比较而言，上海证券市场中非对称效应更明显一些。

参考文献：

[1]聂富强，宋国军沪、深股市波动不对称性的实证分析[J].数理统计与管理，2007（1）：172-175

[2]李亚静，朱宏泉，彭育威基于GARCH模型族的中国股市波动性预测[J].数学的实践与认识，2003（11）：65-69

[3]Engle R FAutoregressive conditional heteroskedasticity with estimates of the variance of United Kingdom Inflation[J].Econometrica，1982（5）：987-1006

[4]Bollerslev TGeneralized Autoregressive conditional heteroskedasticity[J].Journal of Econometrics，1986（3）：307-327

[5]Crouhy and RockingerVolatility Clustering，Asymmetry ang Hysteresis in Stock Returns：International Evidence[J].Financial Engineering and the Japanese Markets，1997（4）：1-35

[6]马明基于GRACH模型的股市波动特征及相关性分析[D].南京：南京理工大学硕士学位论文，2007

[7]李占风经济计量学[M].北京：中国统计出版社，2010：282-287

[作者简介]孔静（1996—），女，江西抚州人，中南财经政法大学2013级统计学专业本科生。