图象的应用及延伸
2016-04-28周宝祥
图象的应用及延伸
◇河北周宝祥
类比是一种常用科学的研究方法.对于直线运动,教科书中讲解了由v-t图象求位移的方法——面积法.此方法可以做适当的延伸,很多物理量都可以用类似的方法求解.近年的高考题也多次体现了这种方法的应用.究竟什么样的物理量可以用这种方法求解,什么样的物理量不可以用这种方法求解呢?下面举例分析.
1面积法的适用范围

A由a-t(加速度-时间)图线和横轴围成的面积可以求出对应时间内做直线运动物体的速度变化量;
B由F-v(力-速度)图线和横轴围成的面积可以求出对应速度变化过程中力做功的功率;
C由F-x(力-位移)图线和横轴围成的面积可以求出对应位移内力所做的功;
D由ω-r(角速度-半径)图线和横轴围成的面积可以求出对应半径变化范围内做圆周运动物体的线速度

小结这道题告诉了我们类比方法的适用范围,只有一个物理量是对另一个物理量的积累时才可以用.
2面积法求功

把蹦床简化为一个竖直放置的轻弹簧,弹力大小F=kx(x为床面下沉的距离,k为常量).质量m=50kg的运动员静止站在蹦床上,床面下沉x0=0.10m.在预备运动中,假定运动员所做的总功W全部用于增加其机械能.在比赛动作中,把该运动员视作质点,其每次离开床面做竖直上抛运动的腾空时间均为Δt=2.0s.设运动员每次落下使床面压缩的最大深度均为x1.重力加速度g取10m·s-2,忽略空气阻力的影响.
(1) 求常量k,并画出弹力F随x变化的示意图;
(2) 求在比赛动作中,运动员离开床面后上升的最大高度hmax;
(3) 借助F-x图象可以确定弹力做功的规律,在此基础上,求x1和W的值.

图1

(2) 运动员从x=0处离开床面开始腾空,其上升和下落时间对称,所以



求得

对整个预备过程,由题设条件和动能定理得
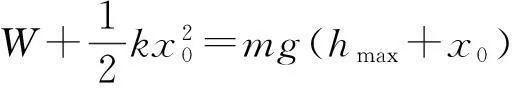
W=2525 J≈2.5×103J.
3面积法求速度


图2 图3
(1) 求电梯在上升过程中受到的最大拉力F1和最小拉力F2.
(2) 类比是一种常用的研究方法.对于直线运动,教科书中讲解了由v-t图象求位移的方法.请你借鉴此方法,对比加速度和速度的定义,根据图3所示的a-t图象,求电梯在第1秒内的速度改变量Δv1和第2秒末的速率v2.
(3) 求电梯以最大速率上升时,拉力做功的功率P.再求在0~11 s时间内,拉力和重力对电梯所做的总功W.

(2) 由加速度的定义式a=Δv/Δt得Δv=aΔt,类比v-t图象,速度的变化量Δv等于a-t图线与坐标轴所包围的面积,故电梯在第1秒内的速度改变量Δv1=0.5 m·s-1.
同理,可以求得前2 s内电梯速度的改变量Δv2=1.5 m·s-1,由于v0=0,所以2 s末电梯的速率v2=1.5 m·s-1.
(3) 当a=0时速度最大.由a-t图象可知,电梯在11 s末速度达到最大,在11 ~30 s时间内做匀速运动,此时拉力F=mg=2.0×104N.由a-t图象面积求得vmax=10 m·s-1,故
P=Fvmax=2.0×105W.
由动能定理,拉力和重力做的总功
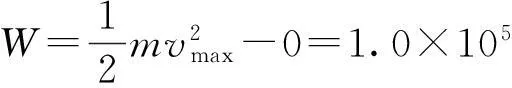
有些题目我们用常规方法来做比较烦琐,甚至很难做出来,这时候我们可以换个角度利用图象来解决,往往会豁然开朗.需要注意的是在应用图象法解题之前,一定要先判断这个方法适不适用.
(作者单位:河北省秦皇岛市抚宁区第一中学)
