利用函数解决生活中的优化问题



利用函数解决生活中的优化问题

■徐凯钦指导老师：刘培训

实际生活当中，经常要碰到一些求解有关费用最省、路程最短、用时最少、利润最大、效率最高等问题，这些问题通常称为生活中的优化问题。根据近年的高考试卷分析，导数与生活的优化问题也逐渐成为高考的热点之一。我们可以利用导数来求解相关函数的最值的方法来解决这类问题。根据题设建立数学模型，借助相互关系寻找各条件间的联系，适当选定变量，构造相应的函数关系，通过求导数来解决实际问题，给出合理最佳的决策方案。

一、函数最值的实际应用问题

解有关函数最大(小)值的实际问题，需要分析问题中各个变量之间的关系，建立适当的函数关系式，并确定函数的定义域，通过创造在闭区间内求函数最值的情境，借助函数的导数这一工具，从数学角度逐步解决实际问题，求得的结果要符合问题的实际意义。

二、实际问题的最大(小)值的解题步骤

(1)建立实际问题的数学模型，写出实际问题中变量之间的函数关系y=f(x)；

(2)求函数的导数f′(x)，解方程f′(x)=0，求出极值点；

(3)比较函数在区间端点和极值点处的取值大小，确定其最大(小)者为最大(小)值。

三、实际生活中的导数应用

根据近年的高考试卷分析，导数与生活的优化问题也逐渐成为高考的热点之一。我们可以利用导数来求解相关函数的最值的方法来解决这类问题。根据题设建立数学模型，借助相互关系寻找各条件间的联系，适当选定变量，构造相应的函数关系，通过求导数来解决实际问题，给出合理最佳的决策方案。

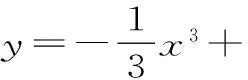
点评：本题考查了导数在实际生活中的应用问题，考查将实际问题转化为数学问题的能力，通过函数关系式的求导、单调性的判断、极值的判断与最值的应用来确定解决实际问题的能力。

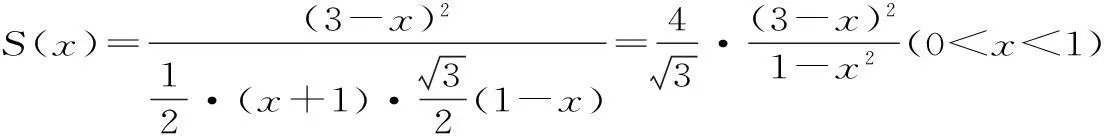
点评：本题考查了利用导数来解决有关的平面几何中的实际应用问题。在解决有关平面几何问题中，当直接处理有问题时可以转化，利用函数的性质来处理有关的问题。通过对函数关系式求导的方法，利用导数求解函数的最值问题。

作者单位：武汉市武钢三中高三(1)班